浅谈有效思维课堂的构建———以直线与抛物线教学为例

朱 聪

（成都新津为明学校，四川 成都）

高中数学是一门对思维的逻辑性和发散性要求较高的学科，因此，在高中数学课堂教学中指导学生掌握有效的思维策略是很有必要的。对学生进行思维训练，可以增强学生的数学领悟力、分析力和运用数学知识解决问题的能力，一旦学生拥有了数学思维，就会拥有强烈的探索欲望，数学学习也会成为学生的一种需要，也会自觉参与。我们的高中数学教师可以以课堂教学内容为依托，以课堂教学手段为途径，循序渐进培养学生的数学思维，本文以直线与抛物线教学为例，从以下几方面对数学课堂中有效思维的培养进行了分析。

一、创设问题情境，激发学生思维兴趣

课堂教学之初，教师可以通过创设问题情境激发学生的思维兴趣，引领学生结合已有的知识系统，通过合理的猜想和推测对新的问题做出分析，然后通过进一步的分析验证自己的猜测，这一过程可以培养学生的直观思维能力，使学生对课堂教学内容产生探究的欲望，为下一步课堂教学的实施做铺垫。以“直线和抛物线的位置关系”教学为例，新课开始之前，老师和同学一起回顾原来讲过的类似的关系，例如直线和圆的位置关系判定，可以通过判断圆心到直线的距离与半径的大小关系，和联立方程两种方式判定，后者指的是联立直线与圆的方程，看这个方程组有没有解，有几个解？有几个解就有几个交点。结合这一情况，请学生进一步对比直线与抛物线关系的判定，猜测一下是否也可以用这两种方法。这时，学生的思维就会活跃起来，将这两种近似的关系进行比较，试图找到其中的相同点和不同点，在此基础上教师进一步点拨引导，通过多媒体演示在同一平面内直线和抛物线之间的位置关系，就会发现：当直线和对称轴平行，直线和抛物线是相交的；当直线和抛物线有一个公共点并且直线不和抛物线的对称轴平行的时候，直线和抛物线是相切关系；当直线和抛物线没有交点的时候，直线和抛物线是相离关系。这种直观的演示可以使看似复杂的问题变得简单明了，教师可以相机引导，在数学题解过程中，直观思维是很重要的化繁为简的方式，可以进一步调动学生的思维兴趣。

二、引导学生自主探究，训练思维能力

学生的数学思维能力还应当包括逻辑思维以及发散思维的能力，教师可以通过引导学生自主探究进行这两种思维训练，探究过程可以结合小组合作形式展开。例如对直线与抛物线交点的判定，教师可以组织学生自由讨论，除去画图这种方法之外，还有什么方法可以得到结论，引导学生尝试几何法与代数法。在这一过程中教师要对学生探究的思路进行规划，关于探究的方向，可以从类似的题目入手，关于探究的方法，可以与相似情况进行对比，最终，学生将这一问题与直线与圆的位置关系进行对比，从中发现由于直线与抛物线的位置在不断变化，因此不能使用几何法，只能通过代数方式验证。在此基础上出示例题，如图：

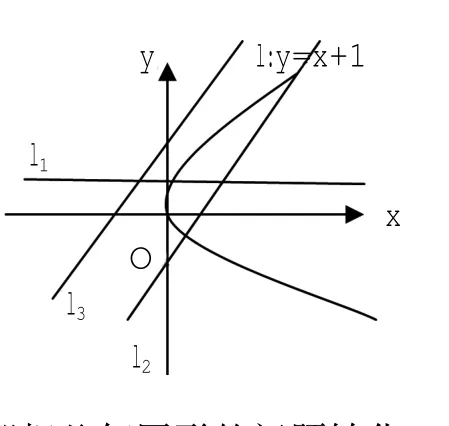
已知直线l:y=kx+1和抛物线c:y2=4x试判断当k为何值时，l与c（1）有一个共同点；（2）两个不同共同点；（3）没有共同点，请学生结合例题判断自己的探究结果是否正确。学生通过将l带入c可得到结论，例题设计思路及目的：通过判断Δ及交点的个数，即把几何图形的问题转化为了代数问题。这个思维过程体现了转化与化归的思想、数形结合的思想。在消元过程中如果得到一元一次方程，则只有一个交点。如果是一元二次方程，就要考虑判别式的大小再做出判断。在此过程中，小组讨论，用代数法解决几何问题，都是教师需要引导学生注意的思维方式。

三、进行思维拓展，培养学生的创造性

培养学生的发散思维能力对于学生自身的发展大有裨益，在数学教学中，教师可以通过课堂内容的进一步拓展，使学生在所学基础上举一反三，对这一类型的问题进行更深入的探究，请学生自己创编习题，是这一训练的有效途径。例如直线和抛物线的位置关系，经过判定，共有相切、相离、相交三种情况，每种情况又可以延伸出与之有关的不同问题，教师可以鼓励学生根据这一性质设计相应的习题，然后在小组之间展开习题竞赛，一组的题目请二组完成，二组的题目请三组完成，以此类推。这样，每个小组为了设计有水平的题目都会竭尽全力，教师可以设计一两个有难度的题目供学生参考，指导学生发散思维的方向，使学生的创造不至于走太多弯路。例如“最值问题”，求抛物线x2=y上一点p到直线l:2x-y-4=0的距离最小值及p的坐标；再比如弦长问题：过抛物线y2=2x的焦点作倾角为45°的直线交抛物线于A、B两点，求线段AB的长。这些题型都是以直线与抛物线的位置判定内容为基础演变而来的，可以以此为范例指导学生的题目设计，从而锻炼学生的发散思维，培养其创造性。

培养学生的思维能力并非一朝一夕之功，也不是通过某一堂课就可以形成的。本文的数学教学思路适合绝大多数的数学课堂教学内容，只要教师在教学过程中结合不同的教学内容有意识地对学生进行思维训练，长此以往，相信学生的数学思维会有一个长足的进步，从而更好地展开以后的数学学习。