基于GM(1,N)_GRNN组合模型的瓦斯涌出量预测研究

高荣翔，曹庆贵，马英琪，周鲁洁

(山东科技大学矿业与安全工程学院，山东 青岛 266590)

0 引 言

瓦斯涌出量预测研究是矿山灾害防治的重要内容之一，也是煤矿企业安全生产监测监控的重要环节。近年来，对于瓦斯涌出量的预测方法除传统的瓦斯含量法、分源预测法、瓦斯梯度法外[1]，国内外学者提出建立灰色模型与神经网络模型相结合的组合模型对煤矿工作面瓦斯的涌出量进行预测，取得了良好的预测效果。在这些研究中，灰色模型的选择多为GM(1,1)1阶1变量灰色模型，对瓦斯预测量直接进行预测，对影响瓦斯涌出的其他影响因素的考虑略显不足。神经网络模型多选用BP(Back Propagation)神经网络模型与RBF(Radical Basis Function)神经网络模型，这两种模型优点明显，结构简单，训练简洁，学习收敛速度较快，但是在训练过程中需要调整的权值较多，存在人为干预的因素，同时需要大量数据进行训练。根据实际生产状况，本文选用GM(1,N)1阶N个变量的灰色模型[2]，考虑煤层埋藏深度、煤层厚度、原始煤层瓦斯含量、煤层倾角、推进速度、瓦斯涌出量等因素。神经网络模型选用广义回归神经网络(GRNN，Generalized Regression Neural Network)模型[3]，GRNN神经网络是一种改进的径向基神经网络，相对于BP、RBF神经网络，逼近能力更强、训练速度更快，样本数据数量较少时，预测效果也很好；它的另外一个优势是网络模型输入原始样本数据后，只需调整平滑参数，避免较多的人为主观因素的影响[4]。

1 灰色-神经网络GM(1,N) _GRNN模型的建立

1.1 GM(1,N)灰色预测模型

灰色系统理论是一种通过已知信息揭示未知信息，将灰色量白化的方法，具有“小样本、贫信息”的特点[5]。灰色系统中运用最多的模型是以时间为序列建立的GM模型，将无规律的原始数据进行一次累加生成，记为1-AGO，简称累加生成，生成有规律的新数列，然后将新数列曲线拟合。考虑到影响工作面瓦斯涌出量的因素众多，灰色模型的建立选用GM(1,N)模型，具体见式(1)～(6)。

i=1,2,…,N

(1)

(2)

B=

(3)

(4)

(5)

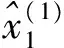
t=2,3,…,n

(6)

1.2 GRNN神经网络预测模型

GRNN广义神经网络模型是美国学者Donald F.Specht在1991年提出的，是一种改进后的径向基神经网络[7]，具有高度容错性和鲁棒性的特点。其扑拓结构与RBF神经网络相似，由输入层、模式层、求和层和输出层四部分组成。不同于RBF网络的是它的逼近速度更快，而且不需要大量的样本数据，更适合非线性数据预测，其结构如图1所示。

图1 GRNN模型扑拓结构

(7)

(8)

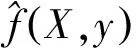
(9)

由公式可知GRNN神经网络的预测精度只与光滑因子σ有关，光滑因子σ越小，处于样本区间内的预测值将无限接近样本数据，处于样本区间之外的预测值无法准确预测；光滑因子σ越大，则预测值无限接近样本数据的平均值。

1.3 嵌入型灰色-神经网络GM(1,N) _GRNN模型

GM(1,N)灰色预测模型与GRNN神经网络预测模型均有各自的优势，预测精度较高，越能获取不错的预测效果。两种模型也存在一些缺点，GM(1,N)灰色模型预测公式不够严谨，GRNN神经网络预测模型对不规律数据处理能力差，经过研究后发现，两者相结合，组成组合模型可以弥补其中的不足，进一步提高预测的准确度。

灰色-广义回归神经网络组合模型有三种组合结构，分别是并联型结构、串联型结构与嵌入型结构。如果采用并联型结构，相当于用两种模型分别进行预测，取结果的平均数，并不能发挥出两种模型的优点。采用串联型结构，先通过灰色模型进行预测，再通过广义回归神经网络对灰色模型预测值进行二次预测，这种预测模型结构也没有将两种预测模型紧密结合，不能使二者的优势最大化。

本文选用嵌入型结构，通过1阶N变量灰色模型将训练样本灰化，把灰化后的训练样本累加数列输入到GRNN神经网络模型中，经过训练确定最佳光滑因子σ，得到训练好的GRNN神经网络模型。之后，将预测样本灰化处理，得到预测样本的累加数列，代入到训练好的GRNN神经网络模型，得到预测累加数列，最后将预测数列白化累减得到预测数值。嵌入型灰色-神经网络GM(1,N)_GRNN模型的预测步骤如图2所示。

嵌入型灰色-神经网络GM(1,N) _GRNN模型充分结合了灰色模型与广义回归神经网络模型二者的优点。在实际生产中影响瓦斯涌出量的各项数据是一组不规则的数据，特殊情况下还会出现较大波动的数值，灰色模型的灰化过程能很好的处理这类数据；而GRNN神经网络预测处理过的数据将更加准确。

2 嵌入型灰色-神经网络GM(1,N)_GRNN模型的应用

2.1 GM(1,N)_GRNN模型应用实例

选取山西某煤矿回采工作面的15组数据作为实例进行预测分析[8]。除监测瓦斯涌出量外，确定其他影响瓦斯涌出的因素，具体包括原始瓦斯含量、煤层深度、煤层厚度、煤层倾角以及推进速度五个因素，详细数据见表1。其中前十组原始数据作为训练样本，后五组原始数据作为预测样本。

图2 嵌入型灰色-神经网络GM(1,N) _GRNN模型流程图

预测过程为：①整理瓦斯涌出量及其影响因素的数据样本，将前十组数据代入到GM(1,N)模型中灰化，作1-AGO累加，结果见表2；②运用MATLAB软件平台搭建GRNN神经网络模型， 将累加数列进行训练，经过四次交叉检验，发现当光滑因子为1.4时，预测效果最好，保存训练好的GRNN神经网络模型,局部代码如图3所示,局部过程图如图4所示;③将需要预测的后五组数据作1-AGO累加，将得到的累加数列输入到训练好的GRNN神经网络模型，得到预测累加数列，再作白化处理，累减得到预测结果;④分别单独运用GM(1,N)模型与GRNN神经网络模型作预测，三种模型预测结果见表3,作出预测结果的折线图以进行直观对比，如图5所示。

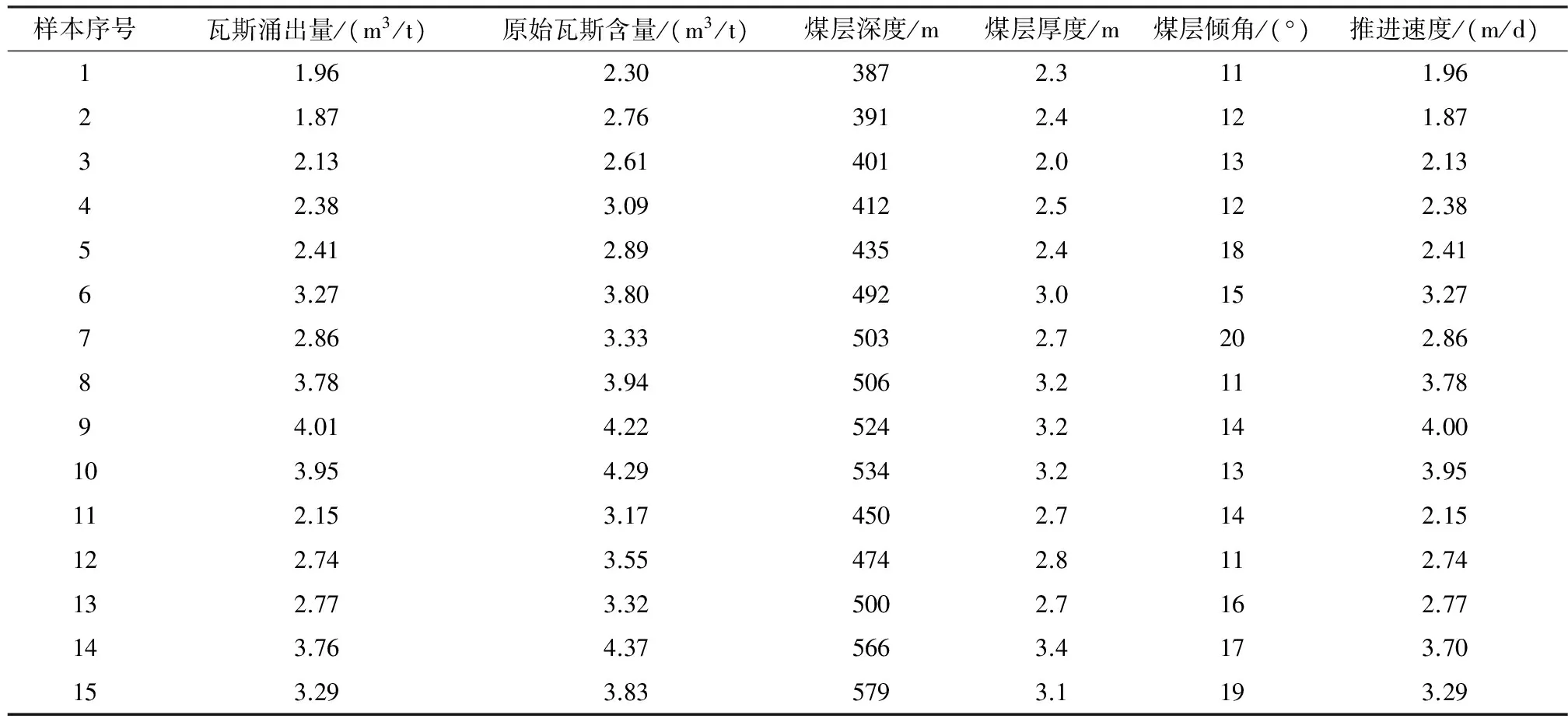
表1 瓦斯涌出量及影响因素

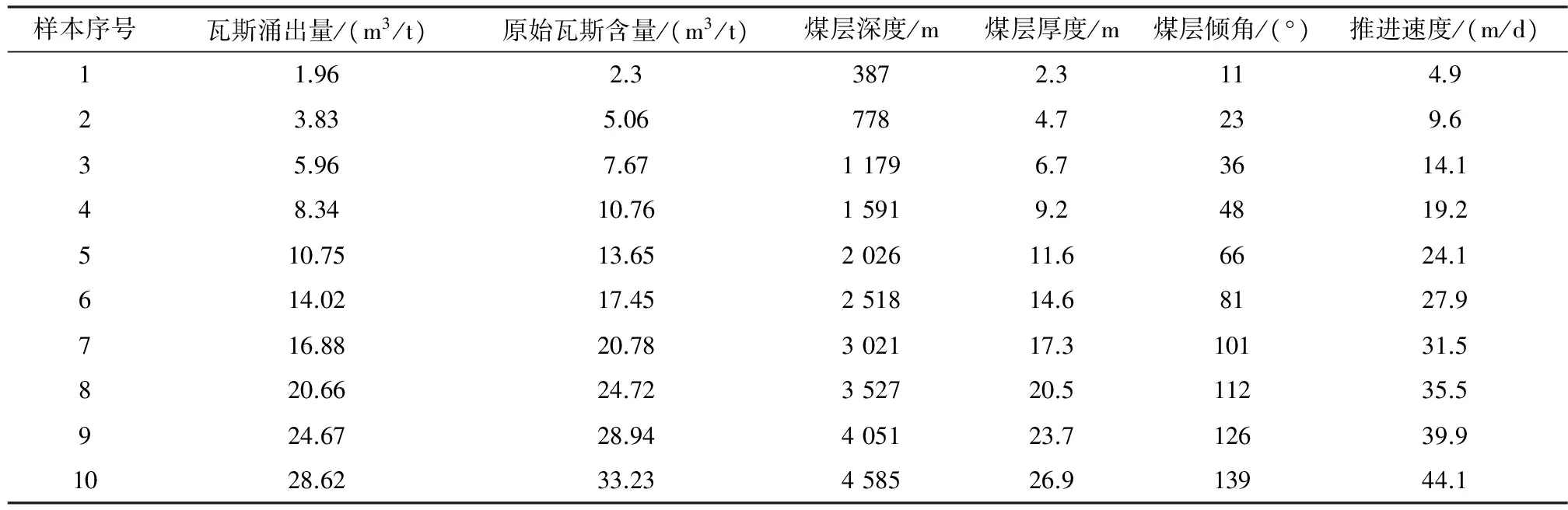
表2 样本数据灰色生成

图3 局部代码

图4 最佳光滑因子

表3 三种模型预测结果对比

样本序号实际值GM(1，N)＿GRNN模型GM(1，N)模型GRNN模型预测值误差/%预测值误差/%预测值误差/%12．152．3549．522．359．302．4212．8622．742．7300．343．0410．942．575．8632．772．7730．132．977．222．644．4343．763．6143．884．1610．633．832．0153．293．4414．613．588．813．558．13平均误差3．709．386．66

图5 三种模型的预测值与实际值对比

由表3可知，应用嵌入型灰色-神经网络GM(1,N)_GRNN模型预测山西某煤矿回采工作面的瓦斯涌出量，预测结果的平均误差仅为3.7%；GM(1,N)模型和GRNN模型单独进行瓦斯预测时，其平均误差分别为9.38%和6.66%。对比发现，组合模型预测结果的平均误差明显优于两种模型单独预测的平均误差。因此，对准确预测工作面瓦斯涌出量，有的放矢的采取瓦斯治理对策，有重要指导意义和实用价值。

仔细分析GM(1,N)_GRNN模型的预测数值，样本1(即表1中的样本11)的瓦期涌出量预测值与实际值的相对误差仍然较大，达9.52%。由表1可见，该样本与之前样本10、样本9等的瓦斯涌出量数据差值很大，数据明确不规律，表明该嵌入式预测模型对不规律数据的处理能力仍有改进余地；而其总体表现具有明确优势，特别在数据规律性较强时优势更为明显。

2.2 GM(1,N)_GRNN模型应用讨论

以上以某一回采工作面为例探讨了嵌入型灰色-神经网络GM(1,N)_GRNN模型在瓦斯预测中的实际应用，说明该模型可准确、方便地预测回采工作面的瓦斯涌出量。通过同样步骤，可将该模型用于煤矿中的某一采区、某一需要研究的区域或者整个矿井，由于没有改变模型的结构及应用方式，显然是可行的，即该模型可准确、方便地预测煤矿中指定区域的瓦斯涌出量。

预测计算应用MATLAB软件进行，说明利用MATLAB软件平台的强大功能，易于搭建灰色模型与广义回归神经网络模型，使数据处理更加方便快捷，快速找出GRNN模型的最佳光滑因子，方便开展GM(1,N)_GRNN模型的预测计算。

3 结 论

1) 本文建立的嵌入型灰色-神经网络GM(1,N)_GRNN模型，可准确、方便地预测煤矿中指定区域的瓦斯涌出量，对煤矿安全生产有重要指导意义和实用价值。

2) 用嵌入型灰色-神经网络GM(1,N)_GRNN模型进行回采工作面的瓦斯涌出量预测，预测结果的精度明显优于单独应用GM(1,N)模型和GRNN模型的预测。

3) 嵌入型灰色-神经网络GM(1,N)_GRNN模型，充分发挥了GRNN模型高度的容错性和鲁棒性、训练速度快、人为影响因素少的优势，发挥了灰色模型处理无规律样本数据能力强的优势，并显示出良好的组合优势。

[1] 张水,曹庆贵,王帅.瓦斯涌出量灰色-RBF网络模型的建立与应用[J].中国矿业,2016,25(10):107-109,127.

[2] 易德生,郭萍.灰色理论与方法[M].北京:石油工业出版社,1992.

[3] 罗毅.基于灰色理论与广义回归神经网络的客运量预测模型研究[D].成都：西南交通大学,2007.

[4] 王文才,王瑞智,孙宝雷,等.基于广义回归神经网络GRNN的矿井瓦斯含量预测[J].中国煤层气,2010,7(1):37-41.

[5] 孟祥健,李秀霞.BP神经网络和GM(1,N)模型在吉林省四平市建设用地面积预测中的应用比较[J].水土保持通报,2017,37(1):173-176,182.

[6] Zeng Bo,Luo Chengming,Liu Sifeng,et al.Development of an optimization method for the GM(1,N) model[J].Engineering Applications of Artificial Intelligence,2016(55):353-362.

[7] 付小平,薛新华,李洪涛.GRNN模型在煤与瓦斯突出及瓦斯含量预测中的应用[J].中国安全科学学报,2012,22(1):24-28.

[8] 宿敬肖,王政,杨静宜,等.优化神经网络模型在瓦斯涌出预测中的应用[J].煤矿安全,2017,48(5):140-143.