基于软件无线电的RS纠错码的实现*

程小枫，柳 松，顾 苏，田 杰，倪 磊

(中国船舶重工集团公司724研究所，江苏 南京 211100)

0 引言

1992年5月，在美国电子系统会议上，MITRE公司的Mitola首次明确提出了软件无线电的概念，其核心是用软件实现尽可能多的无线电功能，即在处理器能力允许的范围内，由软件完成信号的编码、译码、调制、解调、扩频、解扩等功能，强调无线电信号处理的工作由软件而不是专用数字器件完成[1-3]。随着处理器速度的日新月异，越来越多的信号处理算法在工程上得以用软件实现，这里就包括信道纠错编译码算法。

RS码是最大距离可分码(MDS码)[4]，也就是说：在所有的线性分组码中，RS码具有最大的最小汉明距离，所以它的纠错能力是最强的。RS码优良的纠错能力，使其得到了广泛的应用。比如：在军事通信中常以RS(31，15)作为首选码。在深空通信中则常以RS(255，223)作为标准码。在CD-ROM等存储系统中也多采用RS码作为纠错码。目前的高清晰度电视(CHDTV)系统中通常用RS码作为其级联码外码，例如在大联盟HDTV方案中选用的是RS(207，187)[5-6]。

本文以RS(255, 223)为例，先仿真验证了RS算法的有效性和优秀的纠错能力；然后搭建了一个软件无线电通信测试系统，用完全软件定义的形式实现了信道编译码模块；最后用实测数据对比了未使用RS纠错码和使用RS纠错码的误码率，验证了基于软件无线电的RS算法的可行性和有效性。

1 RS纠错码的基本概念

RS码属于一种线性分组循环码，定义在伽罗华域GF(2m)上(m为每个符号比特数)，RS(n,k)码的参数包括：码长n=2m-1，有效信息位长k，校验位长n-k，其中n-k需为偶数，RS码最大能够纠正t=(n-k)/2个m位二进制错误码组。

RS的编码和一般的循环码是相类似的，也是一类循环编码。RS码的编码算法根据变换域的角度分为时域编码算法和频域编码算法。RS码的译码算法比其编码算法复杂得多，现在，用的比较多的并且有代表性的算法是Berlekamp-Messay算法[7](也称为BM算法)与Euclid算法。本文RS编码算法用到的是时域编码算法，而译码算法用到的是BM算法。

2 RS纠错码的仿真

2.1 仿真流程

图1给出了RS(255，223)纠错码的仿真流程。先随机生成223个码字，码字范围为(0，255)；将码字转换至伽罗华域内进行编码运算，将原有223个码字扩展为长度为255的编码串；由于RS(255，223)码最多能纠出16个随机码字错误，因此随机生成16个信道误码；最后译码后转换至实数域即得到接收到的码字。

图1 RS(255，223)的Matlab仿真流程

仿真中用到的部分函数如下：

1)x_gf = gf(x,m)：将码字转换至伽罗华域；

2)code = rsenc(msg,n,k)：RS(n,k)编码；

3)decoded = rsdec(code,n,k)：RS(n,k)译码。

2.2 仿真结果

按照2.1节给出的仿真流程，对RS(255，223)的纠错能力进行仿真。

图2给出了随机生成的223个信源码字；图3是进行RS(255，223)编码后扩展成长度为255的编码串，扩展码放在源码的后面。

图2 信源码字

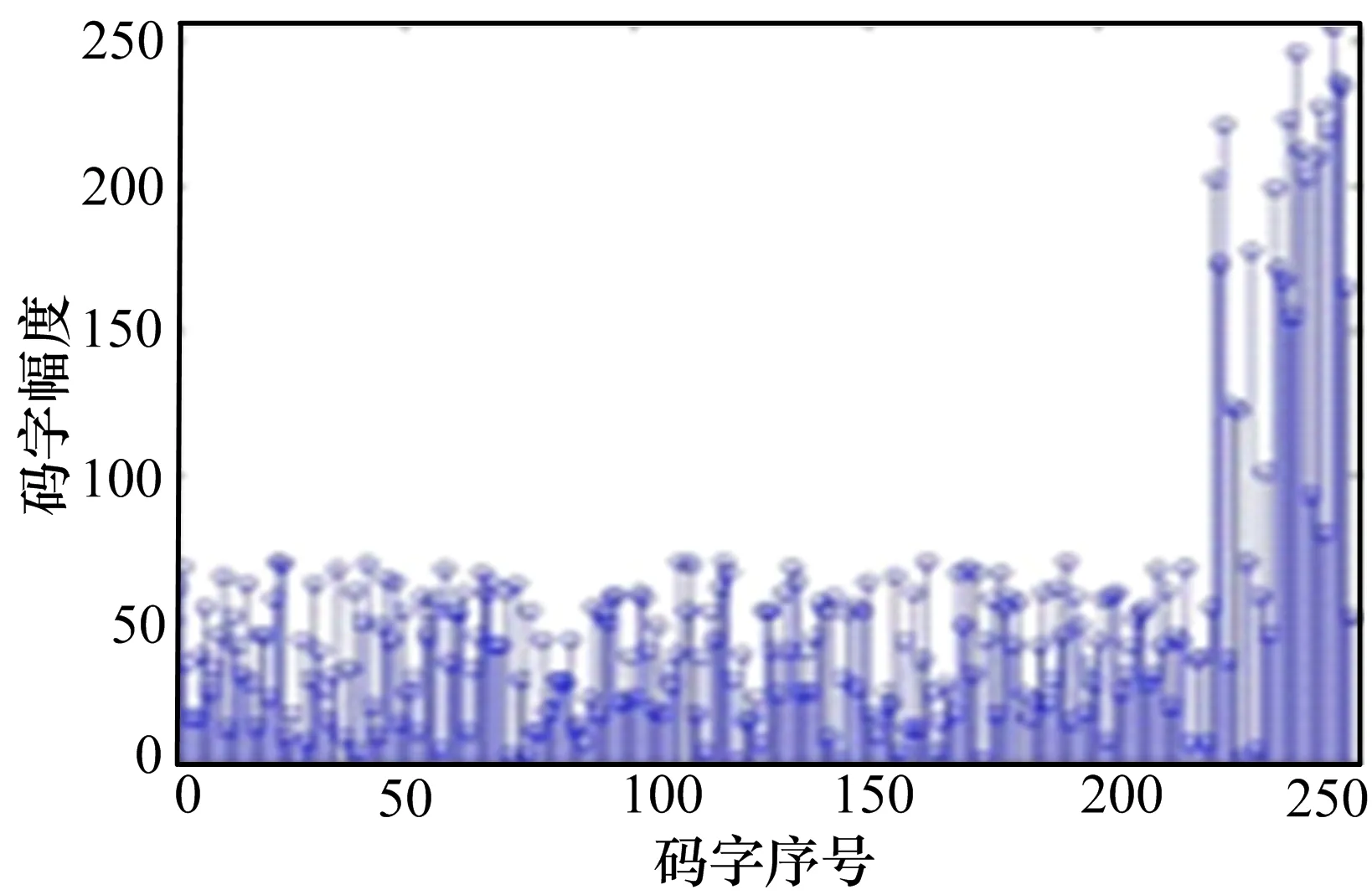
图3 RS(255，223)编码后的码字

图4是随机生成的信道噪声，为区分信源与噪声，仿真时控制噪声幅度较大，噪声出现的位置则是随机出现；图5是编码后的信源加上信道噪声的仿真结果，即接收方收到的信息。

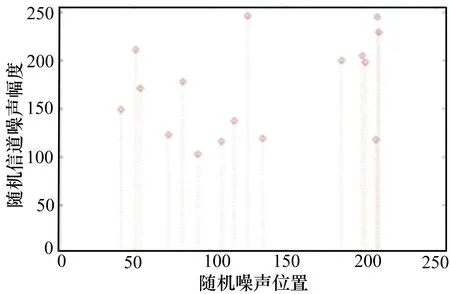
图4 随机信道噪声

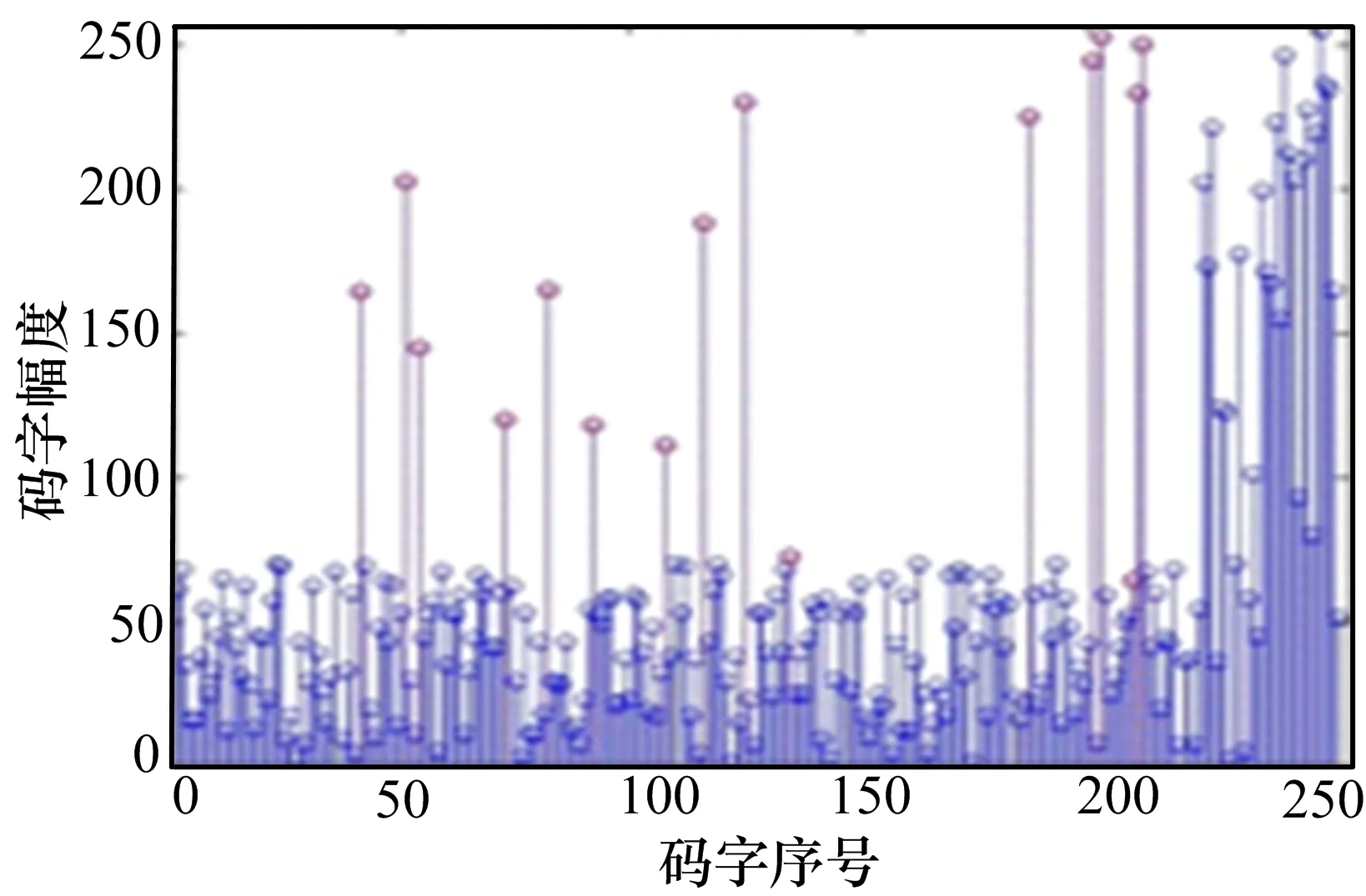
图5 接收方收到的有噪声的信息

模拟接收方对接收到的带有噪声的信息进行RS(255，223)译码，图6即为最终得到的译码后的有效信息。将图6译码后的信息与图2信源信息进行比较，差值为0，如图7所示，即最终得到的信息与信源信息完全一致，16个随机错误全部纠正成功。

3 基于软件无线电的RS纠错码的实现

3.1 软件无线电通信系统

通常一个无线通信系统包含信源编译码模块、信道编译码模块、调制解调模块、 ADC/DAC模块、中频滤波模块、上下变频模块、滤波放大模块、天线发射接收模块。图8给出了本文所搭建的软件无线通信系统的原理示意图，其中信道编译码部分采用了RS编译码。

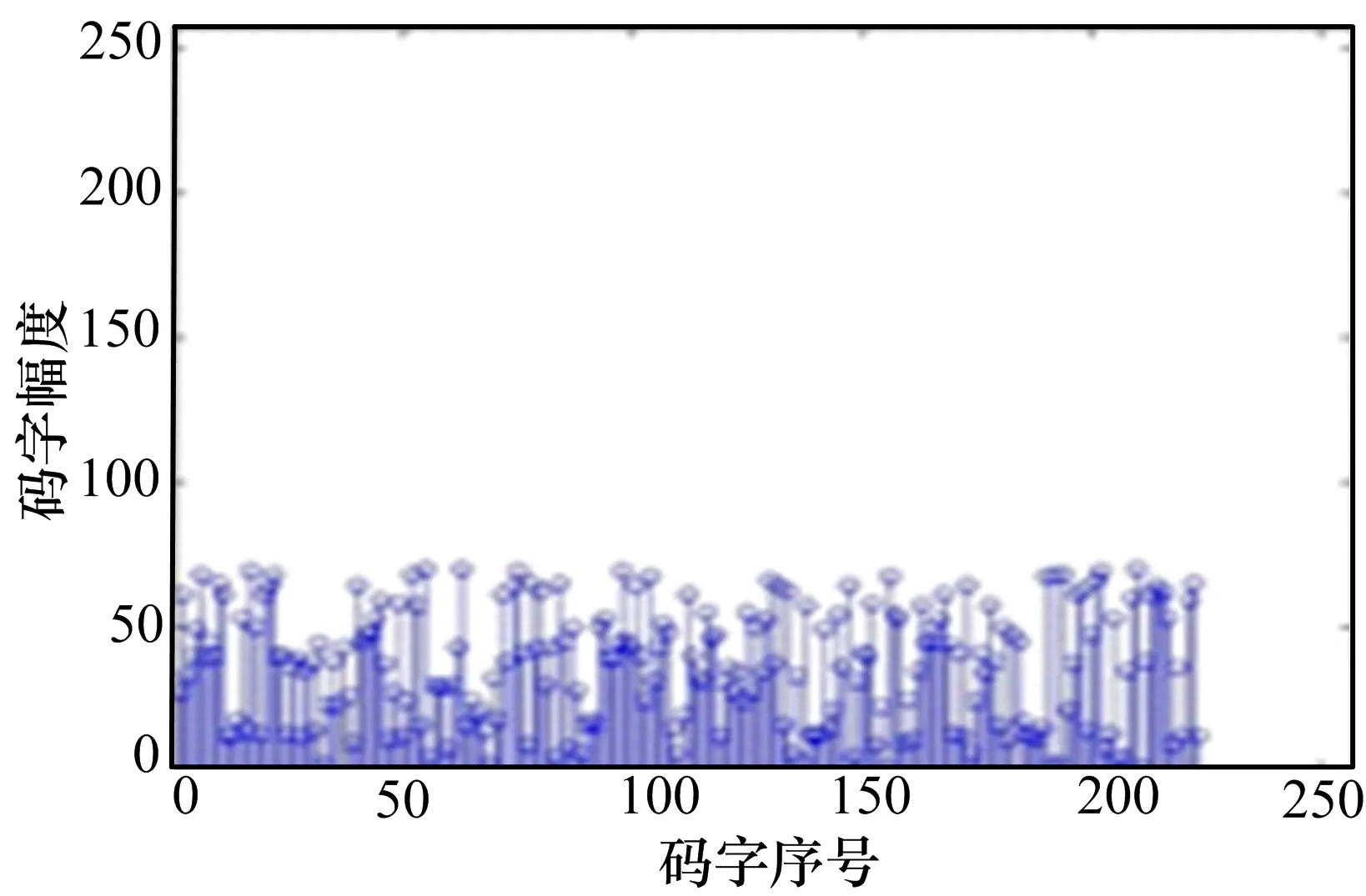
图6 RS(255，223)译码后的码字

图7 译码后信息与信源信息差值

根据软件在无线通信系统中的参与程度，软件无线电也可划分为不同的层次。本文所搭建的软件无线电通信系统在信源编译码模块、信道编译码模块、调制解调模块采用了软件实现，如图8中灰色方框所示，其余模块采用硬件实现。这种软件无线电通信系统也称为软件定义无线电(SDR，Software Defined Radio)。这种系统使用软件对调制、宽/窄带、波形产生等方面的具体应用技术和参数进行控制，不需要对硬件做任何修改，但通常受到频率和带宽的约束，依然存在模拟处理部分，比如还有射频或中频电路。

出于对RS算法验证时，模拟信源和采集数据的方便，本文对上述软件无线电测试系统中的信源编译码模块和信道编译码模块采用了纯软件方法实现，编写了可视化测试软件，运行在普通计算机上。而调制解调模块则使用了FPGA编程实现，并和其它硬件模块集成在一块板卡上，如图9所示。

图8 软件无线通信系统示意图

图10 RS类结构图

图9 软件无线电通信测试系统的信号处理模块

3.2 RS纠错码的软件实现

3.2.1RS纠错码的类结构

本文把RS纠错码的编译码算法封装为一个类——RS类。RS类的接口实现如图10所示。

RS类的各接口功能说明如下：

1)RS_gf()：生成伽罗华域空间，RS编译码的运算都在此空间进行；

2)RS_poly()：得到生成多项式，RS编译码算法需用到此多项式；

3)RS_encode()：RS编码算法；

4)RS_decode()：RS译码算法。

RS类的其它接口包括类的初始化(可用参数控制生成不同的编码长度)、获取信源数据、获取译码后数据等。

3.2.2RS编码算法的软件实现

RS编码算法采用时域编码算法。假定RS(n,k)码，需要编码的信息源的信息多项式为M(x)。时域编码算法步骤可以简单概括为以下三步：

1)将xn-k乘以信息多项式M(x)得xn-kM(x)；

2)然后用xn-kM(x)除以生成多项式g(x)，得到余式即是校验多项式r(x)；

3)将信息多项式M(x)与校验多项式r(x)联接起来即得到RS编码。

图11给出了RS编码算法软件实现的流程图。

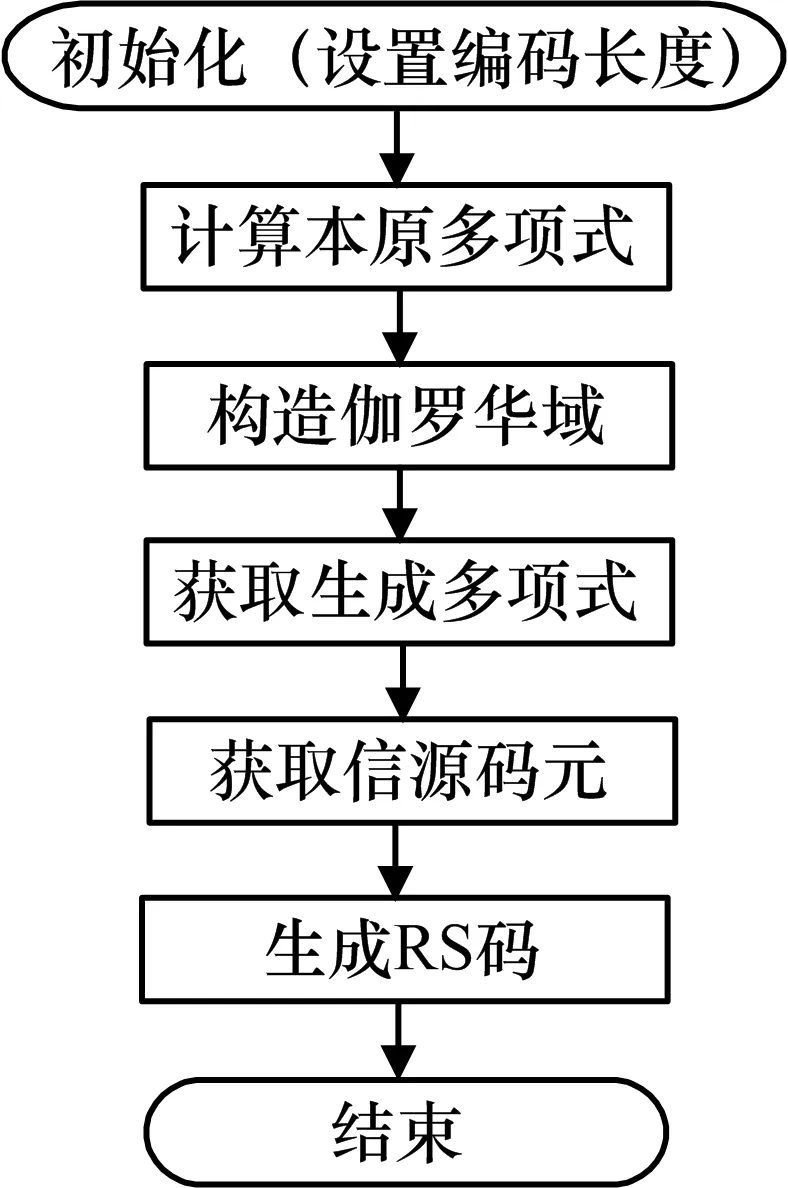
图11 RS编码算法的软件实现流程图

3.2.3RS译码算法的软件实现

RS编码算法步骤可以简单概括为以下三步：

1)由接收到的信息的多项式计算得到伴随式；

2)求错误位置多项式；

3)求错误位置多项式的根。

RS译码算法主要的运算量和复杂度来自于求错误位置多项式，本文用到的是比较具有代表性的Berlekamp-Messay算法(也称为BM算法)。

图12给出了RS译码算法软件实现的流程图。

图12 RS译码算法的软件实现流程图

4 RS纠错码的性能测试

本节利用上节所搭建的软件无线电通信测试系统，对上述RS纠错性能进行测试，测试指标为误比特率。同时作为对照，给出未采用任何信道编码算法的误比特率数据。

4.1 测试方法

按图8所示原理图连接测试用无线电通信系统。发射/接收天线采用定向天线，相距数米相互对准。

在信源端生成所有比特位全为1的信息。对于不采用任何信道编码算法的情况，在接收端统计接收到的误比特数和总比特数，两者相除即得到误比特率。

对于采用RS(255，223)信道编码算法的情况，以223个字节为1组，每组生成32个字节的校验码，与信源有效信息合在一起形成长度为225个字节的编码串。在接收端统计每255个字节中的前223个字节的误比特数和总比特数，两都相除再乘以255/223，即得到有效信息的误比特率。

在信源比特位全为1的时候，RS编码生成的校验码的所有比特位也为1。因此对于采用和不采用RS编码的两种情况，信源端发送的码串从形式上看是一样的，也即在同一次试验中就可同时测试上述两种信道编码的情况。这样，采用和不采用RS编码后的误码数据就完全是在同样的噪声环境和同样的硬件状态下进行的，试验数据更具说服力。

通过调节噪声大小，进行多次试验。

4.2 测试结果

表1给出了15次试验所得误比特率统计数据，每次试验的噪声通过软件控制相应参数依次增大，因为并未实际测量信号功率和噪声功率， 所以上述试验中信噪比并不成比例增大。为取得准确统计数据，每次接收数据量都达到108比特量级，且每次试验均统计相同数据量。

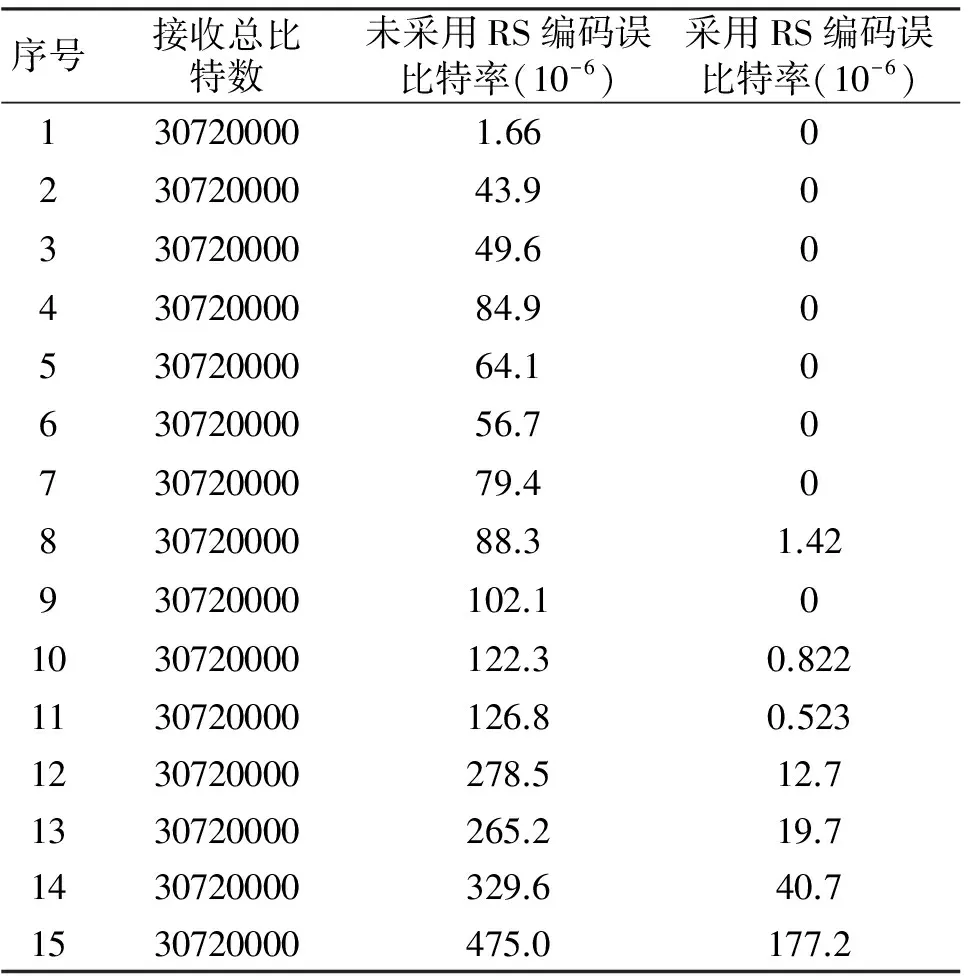
表1 RS编码算法的实际测试结果

由上述统计数据，图13给出了采用/未采用RS纠错编码误比特率对比图。从图中可以看出，在噪声逐渐增大的过程中，未采用RS编码的情况下，误比特率增加得很明显；而采用RS编码纠错后，前面11次试验中基本纠正了所有误码，直到噪声继续增大，才有了明显的误码，但误比特率相比不采用RS纠错码得到较大改善。

图13 采用/未采用RS纠错编码误比特率对比图

5 结束语

本文首先通过对RS纠错码的仿真，验证了RS纠错码的纠错性能； 然后搭建了一个软件无线电通信测试系统，并对RS编译码算法给出了完全软件定义的实现；最后用实测数据验证了RS纠错码的性能。无论是仿真还是实测数据都表明，RS纠错码具有强大的纠错能力，能显著降低误码率；另外，本文给出的RS纠错码的实现方法也顺应软件无线电的发展趋势，对实际工程应用具有一定参考价值。■

[1] Rohde UL , Whitaker JC. 通信接收机：DSP、软件无线电和设计[M]. 北京：人民邮电出版社，2003：58-66.

[2] 向新,张发启,王兴华,等.软件无线电原理与技术[M]. 西安：西安电子科技大学出版社，2008.

[3] Mitola J. The software radio architecture[J]. IEEE Communications Magazine, 1995, 33(5):26-38.

[4] Reed IS, Solomon G. Polynomial codes over certain finite fields[J]. J. Soc. Indus. Appl. Math, 1960, 15(3): 300-304.

[5] McEliece RJ. The theory of information and coding[M]. 北京：电子工业出版社，2003.

[6] 伏静. 软件无线电中的RS编译码的DSP实现[D]. 成都：电子科技大学，2004.

[7] Berlekamp ER. Bit serial reed-solomon encoders[J]. IEEE Trans. on Information Theory, 1982, 28(6):869-874.