波纹管型自调式J-T制冷器充气参数设计研究

马艳红,贾学山

(华北光电技术研究所,北京 100015)

1 引 言

J-T制冷器以其结构紧凑、体积小、质量轻、启动快等优点,已广泛应用于红外系统。根据有无自调机构,J-T制冷器可分为快启动式和自调式两大类,第二代焦平面探测器组件普遍采用以波纹管作为自调元件的自调式制冷器。波纹管型制冷器设计复杂,工作量大,本文在制冷器总体结构和波纹管设计已确定的条件下,讨论充气腔充气参数设计,通过理论分析与实验验证相结合的方式确定充气腔充气参数。

2 充气腔工作过程及热力分析

如图1所示,J-T制冷器自调机构主要包括充气腔、传动杆、波纹管、阀针与阀体。在波纹管型制冷器制作过程中,传动杆与调节器外壳之间预留一定长度,常温下,充气腔内充一定压力的气体,使波纹管压缩,制冷器阀针处于开启状态,制冷器工作时,随着温度的降低,充气腔内压力下降,波纹管拉伸,带动传动杆及阀针下移,实现制冷器流量的自动调节。

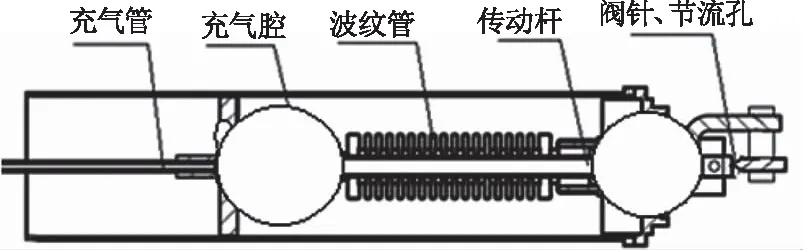
图1 自调机构简图

显然,制冷器的启动过程既是充气腔的变化过程,可分为三个阶段:

第一阶段:波纹管自调前。此时充气腔内充气压力较低,气体可看做理想气体,符合范德瓦尔方程:

式中,a、b是与气体种类有关的范德瓦尔常数；Vm是摩尔体积；R为摩尔气体常数。

第二阶段:波纹管自调中。当制冷器节流孔出现液态工质时,充气腔内气体迅速降温,直至液化,压力降低,带动传动机构对节流孔出气量进行调节。这个阶段属于瞬态过程,理论上比较复杂,而实际意义不大,可不予考虑。

第三阶段:波纹管自调后。自调后流量降低,制冷器处于工作稳定状态,充气腔内气体处于饱和状态,气体参数符合饱和气体状态方程,气体的压力与温度呈一一对应关系,如表1所示。

表1 N2/Ar饱和温度、饱和压力对照表

3 充气工质的确定

3.1 理论分析

制冷器在出液后关闭节流孔,探测器组件的降温时间可达到最快。对于充气腔来说,最好此时所充气体处于临界状态,出现相变。因此充气腔内一般采用的充气介质为氮气、氩气或者某些混合气体。理论上充气介质选择氩气比选择氮气更有优势,这是基于以下考虑:

1)氩气分子比氮气分子大,更不易泄露；

2)氩气是比氮气更惰性的气体,不会影响系统内其他器件的性能；

3)制冷器其他设计参数相同时,启动过程中,充气腔内压力降低,相同饱和温度对应的饱和压力,氩气高于氮气。比如充气腔平均温度为95 K,则制冷器稳定后两种工质充气腔内压差约为3.26 bar,这一差别有利于制冷器的控温稳定性。

3.2 充气工质实验研究

同批次制冷器,主要设计参数为:制冷器预留量:0.4 mm；波纹管刚度600 g/mm；节流孔径0.17 mm；测试条件为40 MPa恒压氮气。充气腔分别充氮气、氩气,从降温时间和控温稳定性两方面对充气工质进行评价。

3.2.1 降温时间对比

同批次制冷器充气腔分别充入10 bar氮气、氩气,其测试结果如表2所示:

表2 不同充气工质降温时间对比表

由实验结果可以看出,制冷器其他设计参数相同时,充氩气的制冷器比充氮气的制冷器降温快。在制冷器工作的第一阶段,气体符合理想气体状态方程,充气压力相同时,充气腔内不同介质对降温时间影响不大,但是在第二、第三阶段,氩气到达饱和温度所对应的饱和压力比氮气低,充气腔内受力平衡先被打破,阀针关闭早,制冷器背压迅速降低,降温方式进入热传导状态,最终降温时间低于充氮气的制冷器。

3.2.2 控温稳定性对比

任取两支分别充氮气、氩气的制冷器,测试其控温稳定性,其对比图如图2所示。由图看出,其他条件不变的情况下,充氩气的制冷器比充氮气的制冷器控温稳定性更好。这是由于制冷器稳定后,充气腔内充气工质为氩气时的压力小于充气工质为氮气时的压力,相当于充气工质为氩气的制冷器预存了一部分预紧力,可以抵消一部分波纹管的残余变形及阀针微小受力变化对流量的影响,从而控温更加稳定。

图2 控温稳定性对比图

综合考虑制冷器降温时间和控温稳定性,建议充气腔充气工质选用氩气。

4 充气压力确定

通过传动机构受力分析及理论推导可得出波纹管外充气型自调式J-T制冷器设计的基础性公式。以我所自行研制的某型号制冷器为例,在制冷器结构及波纹管设计完成后,可通过公式计算出不同预留量所对应的最小充气压力及制冷器的最小预留量；在理论计算的基础上选择几种预留量做充气压力实验,最终确定制冷器充气压力。

4.1 充气压力理论分析

4.1.1 最低充气压力计算

设波纹管形变过程中平均刚度为E,波纹管有效截面积为A,装调传动杆至调节器外壳预留长度为L,外界环境压力为P0,制冷器启动后波纹管刚开始运动时充气腔的压力为Ps。

波纹管刚开始运动时关系式如下:

(Ps-P0)·A=E·L

(1)

即:

(2)

当制冷器开始工作后,如果不计气流的冲击力和各种传动结构的运动摩擦力,只有波纹管外充气腔的气体压力≤Ps,波纹管才能带动传动杆运动。在此之前,阀针没有动作,制冷器以开位状态工作。故此,我们可以计算出充气腔的最低充气压力Pmin。

设充气腔的泄漏率为K,充气腔排出波纹管后的总容积为V,设计寿命为t,并且设定系统在-60 ℃下调节机构仍能正常启动,则存在如下关系:

(3)

即:

(4)

式 (4)是波纹管外充气型自调式制冷器设计的基础性公式。

我所自行研制某型号波纹管型制冷器时,制冷器结构已定,波纹管刚度E:600 g/mm；充气腔泄漏率K:1×10-10Pa·m3/s；设计寿命t:10年,根据公式计算结果如下表:

表3 预留量与最低充气压力对照表

4.1.2 最小预留量计算

图3中,Fp为充气腔气体对波纹管的压力；F0为外界环境气体对波纹管的作用力；Fy为传动杆所受的预紧力；Fk为波纹管的弹力；F为节流孔处喷出气流对阀针的作用力；f为关闭过程中阀针所受的摩擦力；f0为传动杆在行进过程中所受的摩擦力。波纹管形变过程中平均刚度为E,制冷器预留量为L。

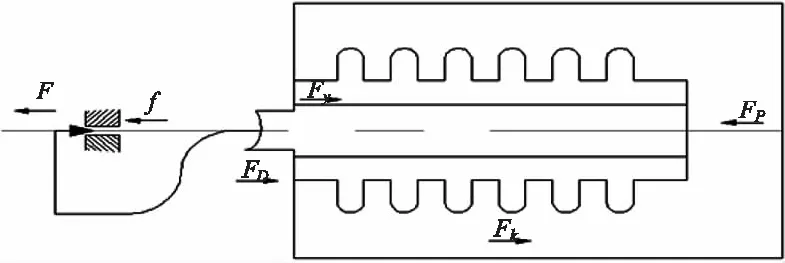
图3 自调机构受力简图

假定传动杆运动不存在加速度,存在如下关系式:

F0+Fy+Fk=Fp+F+f+f0

(5)

计算时,假定制冷器处于理想工作状态,则f=0,f0=0；节流孔处气流对阀针的作用面积是较为复杂的圆锥表面,计算相当复杂,在工程计算时,将其等效为节流孔的面积。此时气流对阀针的作用力最大,则F=S孔·(P-P0),S孔为节流孔面积；F0=P0·S；Fk=E·L；Fp=Pp·S；S为充气腔有效面积；

则式(5)简化为：

P0·S+Fy+E·L=Pp·S+S孔(P-P0)

(6)

启动过程中,随着充气腔气体温度的降低,充气腔内气体压力Fp随之降低,当Fy=0时,自调启动开始。充气腔压力继续降低,FP变得更小,阀针关小甚至关闭节流孔,自调停止。计算时取极限情况,即Fy=0,充气腔内气体处于饱和状态,式(6)转化为:

(7)

在制冷器整体结构及波纹管设计完成后可根据式(7)计算得制冷器最小预留量Lmin,取S孔=0.22 mm,E=600 g/mm；P=40 MPa,计算得Lmin=0.36 mm。

4.2 充气压力实验

制冷器主要设计参数:波纹管刚度:600 g/mm；节流孔径:0.22 mm；充气腔充气工质:氩气；测试条件:40 MPa恒压氮气；测试组件:自行研制的中波320×256 HgCdTe红外焦平面探测器组件。根据理论计算结果做预留量分别为0.4 mm、0.5 mm的充气压力实验,测试制冷器自调时间、降温时间和控温精度,最终确定制冷器的预留量及充气压力。实验结果如下:

预留量取0.4 mm:充气腔充气压力从10 bar增加到14 bar时,部分制冷器始终不自调,经分析认为,受装配精度及零件加工误差影响,制冷器实际预留量不足0.4 mm,当实际预留量小于计算值0.36 mm时,波纹管的最大弹力不能抵消启动过程中充气腔内气体压力及高压气流对阀针的作用力,制冷器不法自调。部分制冷器充12 bar、13 bar时可自调,但控温差,由于HgCdTe组件对制冷器控温精度要求较高,制冷器实际不可用。由测试结果可知,工程应用中,预留量接近极限值,产品成品率偏低。

预留量取0.5 mm:充气腔充气压力从10 bar增加到13 bar,实验结果如表4所示。

由实验结果可以确定,此型号制冷器预留量取0.5 mm,充气压力13 bar合适。

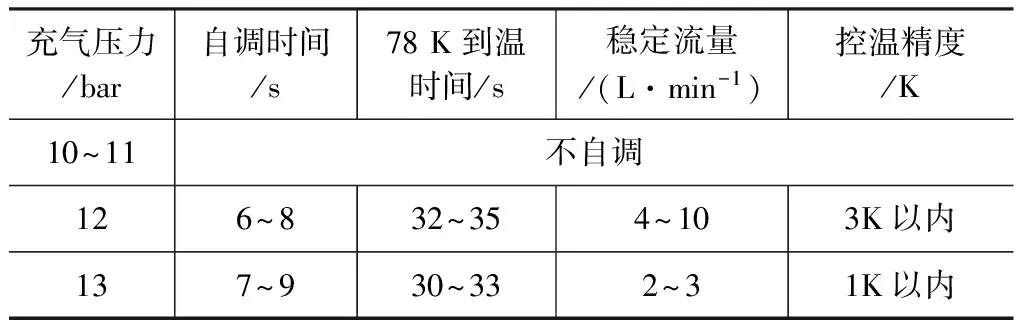
表4 不同充气压力测试结果

最小预留量计算值为0.36 mm,与实际值0.5 mm有偏差,主要因为计算过程中并未考虑传动机构预紧力问题。预紧力与制冷器控温精度密切相关,在预留量设计时,预存相当于阀针开度变化的力及波纹管残余变形力,当波纹管或其他因素引起自调系统受力发生变化时,只相当于改变了预紧力,而阀针开度不变,可提高制冷器控温稳定性。

由表3可知,预留量0.5 mm时,充气腔最小充气压力计算值为10.4 bar,实际此型号制冷器充气压力为13 bar。这主要因为计算时即未考虑预紧力,也未考虑高压气流对阀针的作用力。要求快启动的制冷器一般采用高压、大流量设计,节流孔较大,高压气流对阀针的作用力不可忽略。比如,在充气工质验证实验中,节流孔径0.17 mm,预留量取0.4 mm,充10 bar氩气,制冷器可正常工作且控温较好；但在充气压力验证实验中,节流孔径0.22 mm,预留量同样取0.4 mm,充10 bar氩气制冷器无法自调。

5 结 论

本文采用理论计算与实验结果相结合的方式确定制冷器充气腔最优充气压力和最佳充气工质。制冷器充气腔工质采用氩气,即可有效提高制冷器启动时间,又可提高制冷器控温稳定性；制冷器波纹管设计确定后,充气压力和制冷器预留量有关,通过理论计算与实验相结合的方式可确定制冷器的充气压力与预留量。

[1] S B Chien,L T Chen,F C Chou.A study on the transient characteristics of a self-regulating Joule-Thomson cryocooler [J].Cryogenics,1996,36:979-984.

[2] S B Chien,L T Chen.Two-phase coexistence analysis of the bellows control mechanism for a J-T cryocooler [J].Cryogenics,1999,39:359-365.

[3] WANG Sanyu.Research on self-regulated cryocoolers with bellows[J].Infrared Technology,2006,28(11):651-655.(in Chinese)

王三煜.波纹管型自调式制冷器设计研究[J].红外技术,2004,28(11):651-655.