专家控制半主动悬架系统动态特性分析

2018-03-23王存堂刘烘托谢方伟丁二名

自动化与仪表 2018年3期

王存堂，刘烘托，谢方伟，张晋，丁二名

（1.江苏大学机械工程学院，镇江 212000；2.硅湖职业技术学院机械与汽车工程学院，昆山 215300）

汽车悬架系统[1]是汽车车身与车桥之间的传动连接装置，其作用是传递车身与车桥之间的力和力矩，缓冲外界扰动传递给车身的振动冲击，对其进行衰减，调整汽车行驶中的车身姿态，保证汽车的操纵稳定性和乘坐舒适性。针对悬架系统的性能评价，一般可用车身垂直加速度、悬架动挠度、轮胎动载荷等3个基本参数进行定量分析。半主动悬架系统能够根据路况经控制器实时输出车桥和车身之间所需的系统阻尼力，从而改善这3个性能指标，使悬架系统的减振效果达到最佳。

传统PID算法结构简单，使用灵活，实现方便，普遍应用于工业控制领域，但仍存在难以解决的问题，如调节缓慢、抗干扰能力弱、适应能力差等。当车身发生振动时，传统PID控制的调节时间较长，同时，当汽车车速变化或者通过弯道等干扰情况发生时，此时系统的输出值与设定值之间会发生较大幅度的波动。

在此，结合专家系统智能控制理论和PID经典控制理论，设计了专家PID控制器，利用Matlab/Simulink软件构建出半主动悬架系统模型，对上述3个指标进行仿真及对比分析。

1 数学模型的建立

1.1 路面输入模型的建立

作为车辆主要的振动输入，路面不平度一般采用路面功率谱密度对其统计特性进行描述[2]。当车辆的速度为定值时，汽车的速度时域功率谱密度函数在整个频域内均匀分布，即白噪声信号，因此仿真所用的随机路面输入可通过谱密度的白噪声由积分器产生，随机路面输入为

式中：w（t）为单位白噪声；k0为常数；v为车身速度，m/s；n0为参考空间频率，n0=0.1 m-1，为路面谱高低频的分界线；Gq（n0）为路面不平度系数，m3，为参考空间频率n0下的路面功率谱密度。在此，选取v=50 km/h，利用Matlab/Simulink构造出白噪声积分法路面模型，如图1所示。

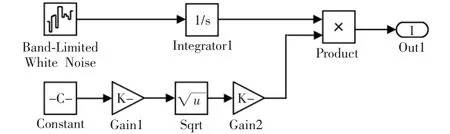
图1 路面输入模型Fig.1 Road input model

1.2 半主动悬架动力学模型的建立

汽车是一个具有时变性和非线性的多输出系统，因此在研究过程中通常对整车进行简化分析。文中以研究上述3个参数为前提，将其简化为二自由度1/4车辆系统模型，如图2所示。

在半主动悬架系统中，阻尼系数包括2部分，即cs为固定阻尼，cr为可调阻尼。其总阻尼力f为

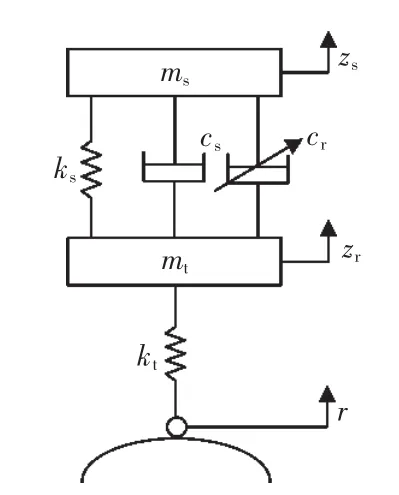
图2 车辆1/4悬架模型Fig.2 1/4 vehicle suspension model

其中由可调阻尼减震器所输出的阻尼力为

由此，得到二自由度1/4车辆模型的动力学方程为

式中：ms为车身质量（簧载质量），kg；mt为车轮轴质量（非簧载质量），kg；ks为悬架减震弹簧刚度，N/m；kt为轮胎等效刚度，N/m；cs为减震器固定阻尼系数；cr为减震器可调阻尼系数；r为路面激励输入；zt为非簧载质量的位移；zs为簧载质量的位移；为车身垂直加速度，m2/s；zs-zt为悬架动挠度，m；kt（zt-r）为轮胎动载荷，N。

取状态向量x1=zs，x2=zt，x3=˙s，x4=˙t，则 X=；以车辆的车身垂直加速度、悬架动挠度、轮胎动载荷3个参数为性能指标输出，令Y=，其中 y1=¨s，y2=zs-zt，y3=kt（zt-r）

2 专家PID控制器的设计

专家系统[3-4]是一个智能计算机程序系统，其知识库包含了某个专业领域内专家拥有的知识水平和丰富的经验，可以利用专家水平的推理能力和解释能力解决该领域内相应问题，以获得类似于专家水平的结论。

专家PID控制的实质是：基于受控对象和控制规律的各种知识，无须知道被控对象的精确模型，利用专家经验设计PID参数，实现系统的智能控制。该系统结构如图3所示。

图3 专家PID控制系统结构Fig.3 Expert PID control system structure

文中，以悬架系统为受控对象，取车身加速度为设定值r，令e（k）为在当前采样时刻车身加速度实际值 y 与设定值 r之间的偏差；e（k-1），e（k-2）分别为离散化的前1个采样时刻、前2个采样时刻车身加速度实际值与设定值之间的偏差值，则有

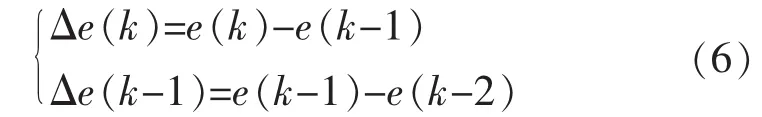
根据车身加速度误差及其变化，建立Δe（k）=0偏差与控制量之间的映射关系，实时调节半主动悬架系统的可变阻尼力，控制器按照以下规则设计相应的控制算法：

1）当 e（k ）≥M1时，M1为根据车辆的制造标准设定的误差界限，表示加速度偏差的绝对值处于大误差范围，因此不考虑偏差此时的变化趋势，直接将可变阻尼力u（k）按系统的最大值输出，抵消外界的冲击，使加速度偏差的绝对值迅速减小，相当于开环控制。

若 e（k）≥M1，则u（k）=UPB，式中 UPB为控制器输出的最大阻尼力；

若 e（k）≤-M1，则u（k）=UNB，式中 UNB为控制器输出的最小阻尼力。

2）当 e（k）Δe（k）＞0 时，表示加速度偏差的绝对值为增大的变化趋势，或此时误差为一常值，没有发生改变。

若 e（k ） ≥M2，M2为根据车辆制造标准设定的误差界限，且M2＜M1，表示加速度偏差处于较大的误差范围，可由控制器输出一个较大的阻尼力，以较快的速度减小加速度偏差的绝对值，此时控制器的输出为

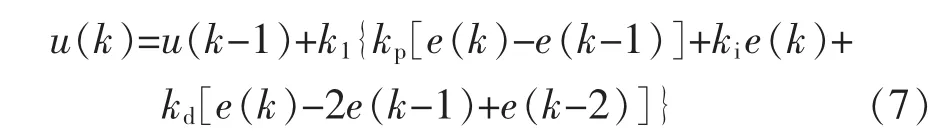
式中：u（k-1）为前1个采样时刻控制器输出的阻尼力；k1为增益放大系数，k1＞1；kp，ki，kd分别为 PID 控制的比例、积分、微分系数。

若 e（k ）＜M2，表示加速度偏差处于较小的误差范围，可由控制器输出一个较小的阻尼力，使加速度偏差的绝对值以较慢的速度减小，直至达到要求的范围内，此时控制器的输出为

3）当 e（k）Δe（k）＜0，且 Δe（k）Δe（k-1）＞0 或e（k）＝0时，表示加速度偏差的绝对值为减小的变化趋势，或者加速度已经达到最优状态。此时保持控制器的输出不变。

4）当 e（k）Δe（k）＜0，且 Δe（k）Δe（k-1）＜0 时，说明加速度偏差正处于极值状态。

若此时 e（k）≥M2，加速度偏差处于较大的误差范围，可由控制器输出一个较大的阻尼力，即

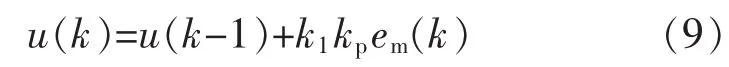
若此时加速度偏差处于较小的误差范围即e（k）＜M2，可由控制器输出一个较小的阻尼力

式中：em（k）为误差e的第k个极值；k2为抑制系数，0＜k2＜1。

5）当 e（k ）≤ε 时，ε 为根据控制器的精度选择的任意小的正整数，表示加速度偏差的绝对值处于很小的误差范围。为使加速度偏差更趋于设定值，可合适的采用积分环节，提高系统的性能。

在Matlab的m文件编辑器中，编辑基于上述专家PID控制规则的S-Function程序[5]，完成后以M函数形式保存，然后再在Simulnik的自定义组中选择S-Functoin模块，再将保存好的m文件添加进去，即可。

3 仿真分析

车辆的参数[6]见表1。利用Matlab进行编程仿真，系统仿真的输出量为车身垂直加速度、悬架动挠度、轮胎动载荷3个参数。

表1 车辆1/4模型参数值Tab.1 1/4 vehicle model parameters

半主动悬架控制器的Simulink程序如图4所示。3种悬架相同的输出量通过同一个示波器显示，将表1所示参数代入Simulink程序中进行仿真[7]，仿真完成后得到相应的输出量对比结果，如图5所示。

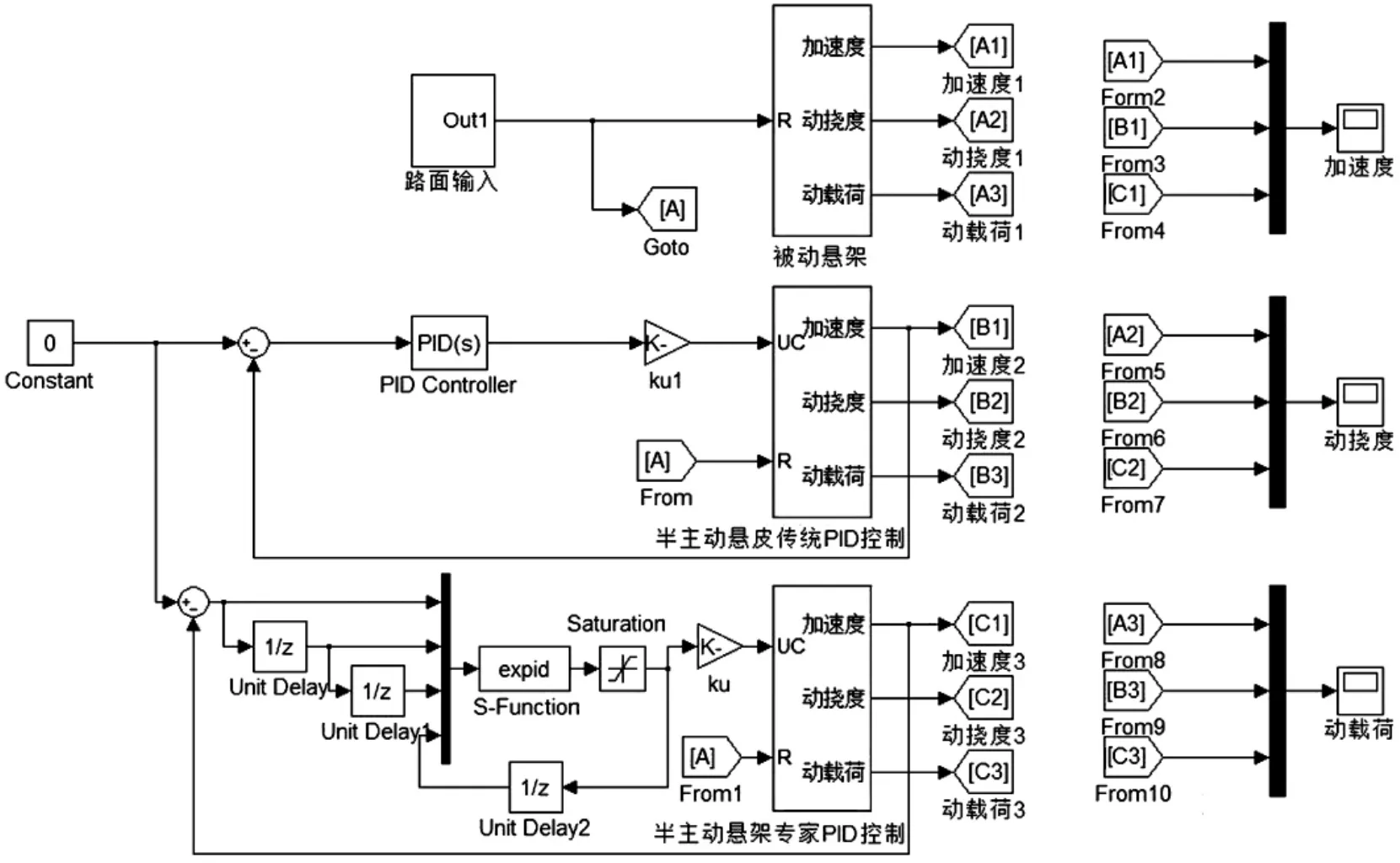
图4 半主动悬架控制器仿真模型Fig.4 Semi-active suspension controller simulation model

图5 3种悬架系统的性能曲线Fig.5 Performance curves of three kinds of suspension systems

由图5（a）可见，相比于被动悬架，具有PID控制器的半主动悬架，可以将车身垂直加速度指标维持在相对较小的范围内，而具有控制规则的专家PID控制半主动悬架，则可以进一步地降低该指标，从而更好地缓解由于车身上下振动而造成的不舒适感。

由图5（b）可见，被动悬架的动挠度区间最大，PID控制半主动悬架次之，专家PID控制半主动悬架最小，可以减小行驶过程中减振器撞击限位块的程度，故能够更好地发挥车辆的行驶平顺性。

由图5（c）可见，PID控制半主动悬架与专家PID控制半主动悬架的轮胎动载荷区间范围较为类似，相对于被动悬架，均有较大的改进，轮胎上下跳动范围较小，较好地优化了车辆的操作稳定性。

依据图5的悬架性能曲线，可以分别得到3个参数在3种悬架下对应的峰值、谷值和均方根值，结果见表2。

4 结语

通过对3种悬架系统时域内的仿真结果进行相应的数值分析，相比于被动悬架，可知：PID控制半主动悬架的车身垂直加速度峰值下降了35.9%，专家PID控制半主动悬架的车身垂直加速度峰值下降了70%；PID控制半主动悬架的悬架动挠度峰值下降了38.1%，专家PID控制半主动悬架的悬架动挠度峰值下降了60.5%；PID控制半主动悬架的轮胎动载荷峰值下降了37.5%，专家PID控制半主动悬架的轮胎动载荷峰值下降了43.9%。