基于土拱效应室内模型试验的理论分析

2018-03-22陈强梁海安郭瑞峰阚霏云邵伟吕美美

重庆建筑 2018年3期

陈强，梁海安，郭瑞峰，阚霏云，邵伟，吕美美

（东华理工大学建筑工程学院，江西南昌 330013）

0 引言

自太沙基证明土拱效应以来，土拱效应广泛应用于隧道、基坑开挖、加筋土、被动桩、挡土墙及桩承式路堤等众多工程领域，但其实际应用经验领先于理论发展。目前土拱效应的理论分析方法大致可以分为两种。一种是取单元体受力平衡进行分析：如国外的太沙基计算法[1]和H&R法[2]等理论计算方法，国内的有陈云敏[3]、赖汉江[4]等提出的改进H&R法、朱碧堂[5]等提出的拱形梁法、刘吉福[6]提出的桩土应力比计算以及余闯[7]等改进的多拱理论解等，根据这些分析方法可以推算土拱效应下土压力的分布或桩土应力比。

另一种基于抗滑桩间距的研究，利用摩尔库伦强度破坏准则对抗滑桩间的土拱效应进行分析。贾海莉等[8]对抗滑桩及护壁桩之间的土拱效应进行了分析，假设土拱拱轴线为抛物线，利用土体的抗剪强度对最有可能发生破坏的拱顶及拱脚处截面进行验算。周德培[9]、熊良宵[10]、吴坤铭[11]等基于边坡工程中的抗滑桩之间的土拱效应，提出了以桩间极限状态下的静力平衡条件、跨中截面强度条件以及拱脚处截面强度条件共同确定桩间距。王乾坤[12]同样基于抗滑桩桩间土拱力学特性分析，提出了以桩间土体的摩尔库伦破坏准则、土体的力学平衡和桩间土体的绕流阻力共同确定临界桩间距的方法。焦赟[13]等建立了地震作用下的土拱效应力学分析模型，同样基于摩尔库伦的强度准则得出桩间净距。

本文通过室内平面应变模型形成直观的土拱现象，研究了回填地基中土拱效应的力学机理。在其他学者研究的基础上推导出砂性土中土拱效应的理论计算公式，并利用摩尔库伦强度破坏准则对比分析计算验证了推导公式的可行性。研究成果可为后续室内试验和工程应用的理论分析提供参考。

1 室内模型试验

1.1 试验装置

室内试验采用1m×1m×0.2m 的自制模型箱，箱体的顶部敞开，便于实验过程中的填土、堆加荷载等操作，底部设有0.8m×0.2m的活动门，活动门上方放置一块预留了孔洞的木板。预留孔洞为宽度较窄的矩形孔，满足平面应变条件，孔洞的大小根据试验目的，分别为0.1m、0.2m、0.3m、0.4m及0.5m。箱体的正面采用透明耐力板，便于观测试验现象。

1.2 试验材料

试验采用两种不同的土样，编号A、B。通过筛析法得到砂土颗粒大小的分布曲线（见图1、图2），分别对土样A、B的级配指标进行计算，计算结果如表1所示，土样A为良好级配土而土样B为不良级配土。

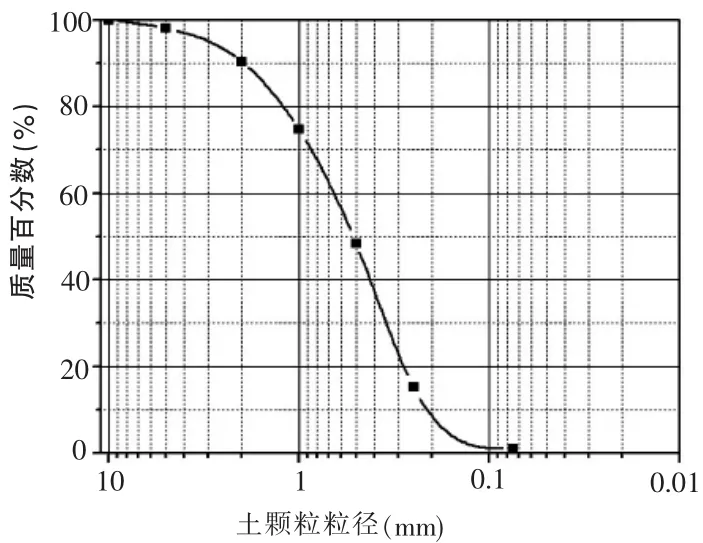
图1 土样A的颗粒大小分布曲线

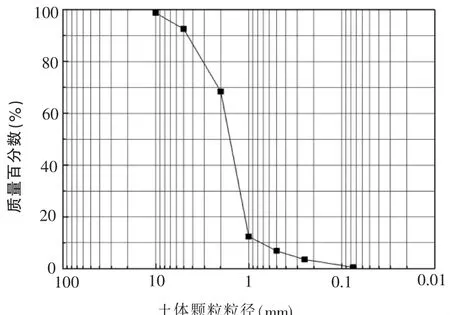
图2 土样B的颗粒大小分布曲线

表1 级配指标计算

1.3 试验现象

试验过程中相关系数如表2所示。

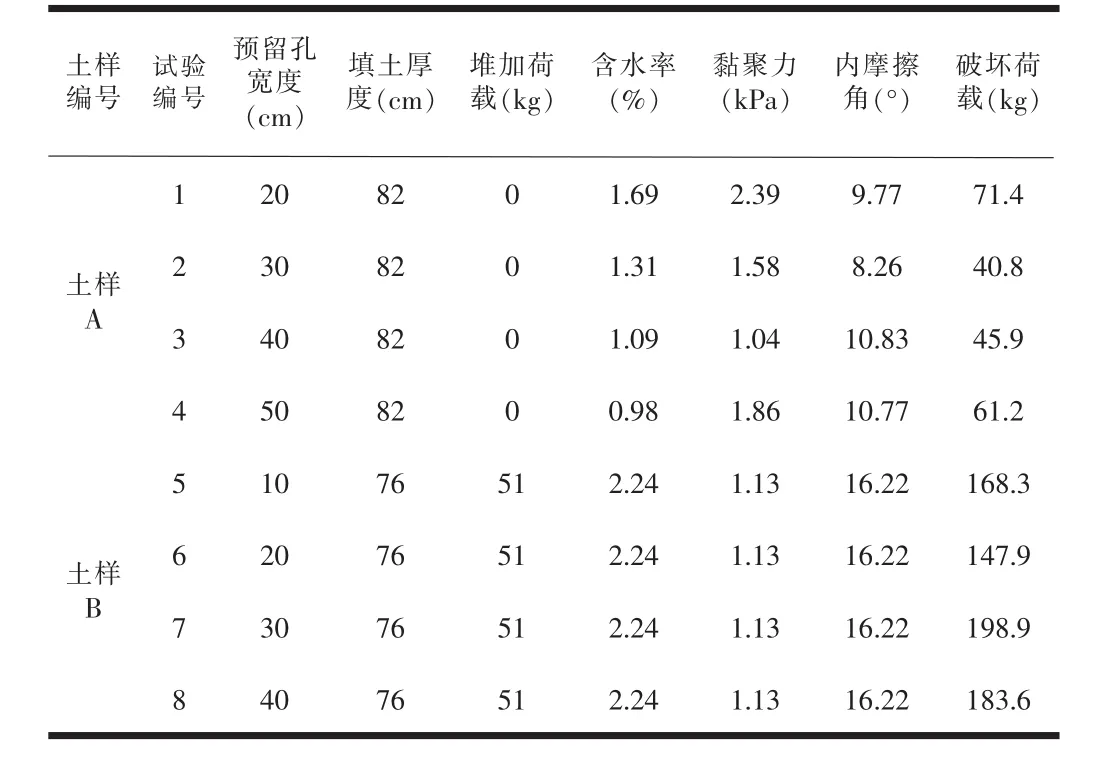
表2 试验相关参数表

打开活动门后，在堆载作用下，模型箱中土体应力重新分布，预留孔处的土体沉降较大以致发生塌陷。预留孔两侧木板为土拱的形成提供了直接拱脚，试验中该拱脚的存在形式较为稳固，土拱的破坏无法从拱脚开始，土体在应力转移的过程中，直接从土拱顶部开始破坏，所形成的土拱为瞬间拱，处于不稳定状态，随后土体发生完全破坏，即土体泄漏至上下层贯通。因此，在理论计算过程中，只对拱顶的破坏机制进行了分析计算。

2 试验结果理论计算

2.1 室内模型土拱受力分析

根据试验记录的图像统计分析的结果验证了砂性土中的土拱形态为抛物线形，为“合理拱轴线”，其任一截面上只存在压力，没有弯矩和拉力。因此，建立了如图3所示的抛物线形土拱受力模型。

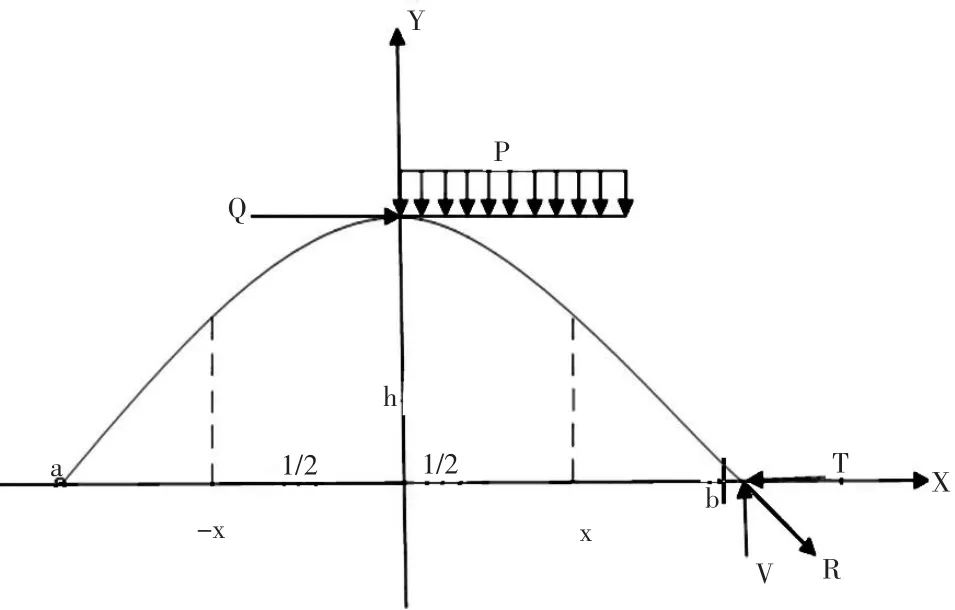
图3 土拱形状示意图

为了简化土拱的受力分析，做出的基本研究假设包括：形成的土拱为平面应变下的土拱，且土拱厚度对土拱没有影响；土体为理想的均质、各向同性的半无限弹性体；回填土上的荷载为竖直均布荷载；预留孔两侧为土拱提供稳定的拱脚。

假设土拱拱高为h，拱跨为l，则半拱跨度为l/2。取半个拱进行受力分析，P为拱上均布荷载Q为另一半拱的反力，拱脚处的合力为R，T和V分别为拱脚反力水平方向和竖直方向的分力。由于拱上任一点（x，y）都不存在弯矩。

根据静力平衡：

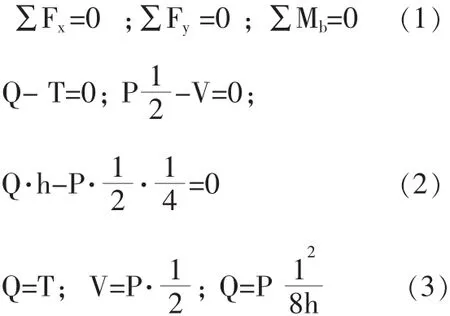
拱脚处合力

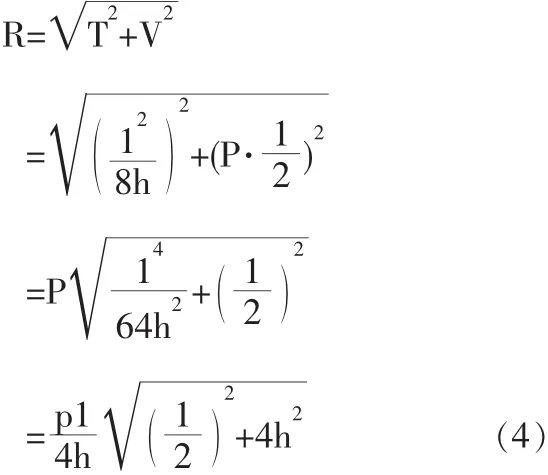
对拱上任一点的压力有

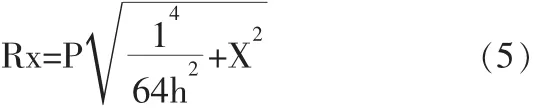
试验研究表明，砂性土中布置适当的“桩体”可以有效地降低土体的不均匀沉降和提高土体承载力，这是由于砂性土中可以形成土拱效应，“桩”为土拱效应提供了直接拱脚，限制了桩体间的土体的连续崩塌。如图4所示，P为堆加的均布荷载，G为土体的质量。由图4可以看出，位于预留孔上方的荷载与土体自重由预留孔两侧木板和土拱共同承担，传递到预留孔两侧木板上的力通过模型箱下的钢架传递到地面。因此，试验中土拱很难在拱脚a、b处发生破坏，主要破坏模式是拱顶c处的土体塌陷，试验现象很好的证实了这一点。

图4 室内模型受力示意图

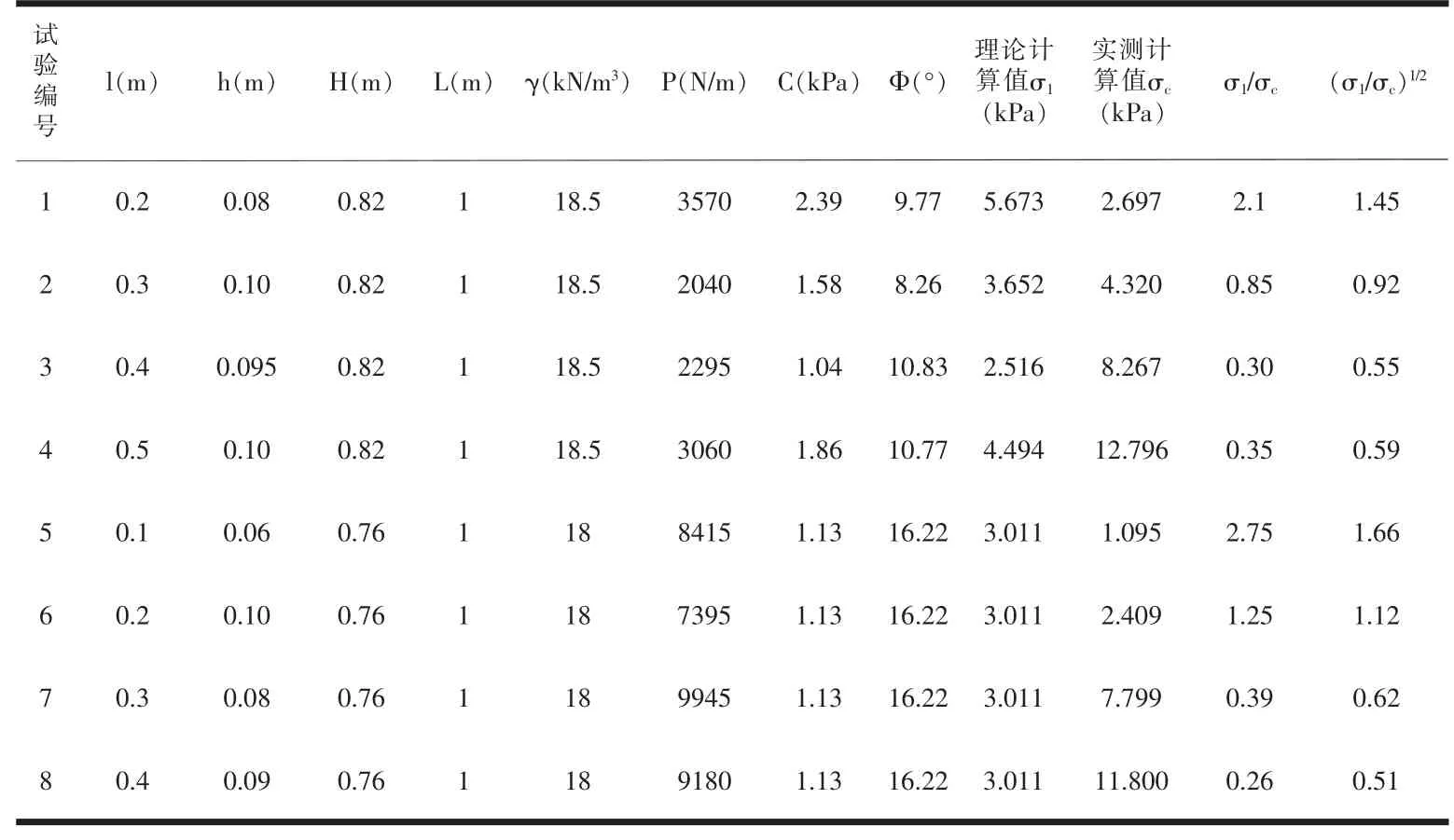
表3 理论计算值与试验实测计算值对比

由于荷载与自重的传递主要通过竖向土拱起作用，而且试验模型为平面应变模型，水平向的土拱作用忽略不计，因此，理论分析只针对竖向土拱。

由式（5）可得，拱顶c处的压力

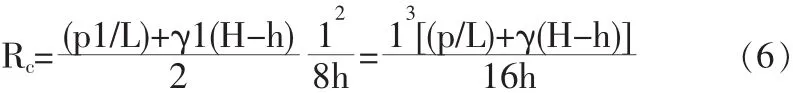
则拱顶c处竖向应力实测计算值

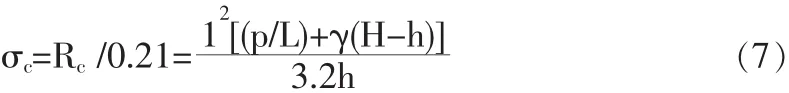
式中：H为回填土的高度，m；L为模型箱的宽度，m；h为直观土拱的高度，m；l为直观土拱的跨度，m；p为堆加的均布荷载，N/m。

2.2 摩尔库伦破坏准则

摩尔库伦理论破坏准则为τf=c+σtanφ。其中，c、φ分别为土体黏聚力和内摩擦角。

根据土力学，假设某一土体单元上作用着最大主应力σ1和最小主应力σ3，σ1=σ3tan2（45°+φ/2）+2ctan（45°+φ/2）或σ1=

根据摩尔库伦强度准则，在拱顶c处满足单向应力状态，即σ3=0。根据应力圆几何条件及单向受压摩尔库伦强度准则，

2.3 计算结果分析

为验证本论文推导出的土拱破坏理论计算方法，以室内模型试验堆载作用下土体破坏荷载值进行计算，与摩尔库伦强度破坏准则得出的理论值进行对比分析。

由表3中计算结果可以看出，按照本章所推导的计算方法得出的拱顶处土体破坏的应力值与摩尔库伦强度破坏准则得出的理论值相比较，两者之间差别较大，但存在一定的规律性。土样A与土样B的试验计算值在拱跨为0.1m时和0.2m时大约为理论值的1～3倍，而在拱跨为0.3m、0.4m及0.5m时大约为理论值的0.25～0.9倍。产生误差的主要原因是推导的计算方法中土拱拱跨取预留孔宽度，而未考虑土拱厚度的影响。根据公式（7）可以看出计算的结果会偏小。其次是推导的计算方法假定了上部堆加的荷载是均匀分布的，且在试验过程中当拱跨大于0.3m时，模型箱两侧的边界效应对土体破坏荷载产生的影响。所以，本文推导的计算方法的计算结果在拱跨小于0.3m时要小于理论结果，在拱跨大于0.3m时又大于理论结果。

为了能够较为准确地计算出室内试验时堆载作用下砂性土中形成的土拱在破坏时拱顶处的应力，考虑形成土拱厚度的影响，重新假设拱跨t=ζl，则改进后拱顶c处竖向应力，由此得到ζ=（σ1/σc）1/2。根据表3中的计算结果，系数ζ取1.0～1.5，改进后的公式计算结果见表4。