RBF神经网络补偿的并联机器人控制研究

彭志文，高宏力，梁 超，文 刚

（西南交通大学 机械工程学院，四川 成都 610031）

1 引言

三自由度Delta机器人是食品、药品分拣包装等生产线上的关键组成部分[1]，由于机构三个运动支链对称安装使其有着刚度大、无累积误差等优势。在系统的控制方面，机构的并联特性使其成为一个高度耦合的非线性系统。针对系统的解耦控制，基于动力学模型的控制算法跟踪效果优于传统的运动学控制。目前，被广泛应用的是计算力矩控制策略[2]。在系统动力学模型可以准确推导的前提下，计算力矩法可以实现对理想轨迹准确的跟踪[3]。在实际运用中，由于存在很多干扰和不确定性，只能推导出理想情况下的系统动力学模型，而不能获得被控对象的真实模型[4]。针对并联机器人的模型强耦合性和不确定性，文献[5]提出了一种模糊PD控制策略，详细的分析了系统噪声来源。针对Delta机器人，提出一种计算力矩法基础上的RBF神经网络在线补偿控制策略。RBF神经网络结构简单，运算量小，泛化能力较强，可以很好的应用于要求实时性的机器人运动控制。在RBF神经网络中，无需进行离线训练，实时运行中以关节角度误差及其变化率作为网络输入，得到力矩补偿值和计算力矩的输出共同控制系统实现对目标轨迹准确跟踪。

2 计算力矩控制策略

针对三自由度Delta机器人，基于虚功原理法建立机构动力学方程。与其他工业机器人相似，Delta机器人动力学方程也能够表示为如下形式

式中：M（α）—质量惯性矩阵；C（α，α˙）—柯氏力和向心力矩阵；

N（α）—重力矩阵；α—驱动臂转动角度向量；τ—驱动臂驱

动力矩；τ—外部扰动。

由式（1）可以看出系统具有很强的非线性和耦合性。一般的基于动力学设计的计算力矩控制策略如下：

式中：M^（α）—质量矩阵分项的估计；C^（α，α˙）α˙—科氏力、向心力分项的估计；N^（α）—重力分项的估计；e—关节位置误差；e˙—关节速度误差；Kp，Kd—控制参数矩阵。

在理想情况下，即假设动力学建模准确，系统名义模型与实际模型一致且无外部扰动。有M^（α）=M（α），C^（α，α˙）=C（α，α˙），N^（α）=N（α）。将式（2）代入式（1）可得系统闭环误差方程为e¨+Kpe+Kde˙=0 。在实际应用中，几乎不可能得到完整真实的模型，存在各种确定和不确定的外部扰动。那么名义模型与系统真实模型之间存在偏差ΔM=M-M^，ΔC=C-C^，ΔN=N-N^。因此在实际情况下，系统闭环误差方程为

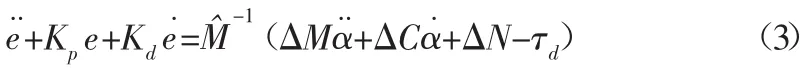
由式（3）可知，用普通的计算力矩控策略无法使误差收敛到0。

3 RBF神经网络补偿控制策略

3.1 RBF神经网络结构

RBF网络结构简单，是一个单隐层前馈网络，具有很强的泛化能力。RBF网络已经被证明能够以任何精度逼近任何非线性函数[6-7]。不妨设 X=［x］T为网络输入，隐层是径向基函数 H=［h］T，

ij为高斯基函数，表示隐层第j个神经元的输出。Cj=［cj1，cj2，…cjm］为RBF网络节点j的高斯基函数中心。b=［b1，b2，…bm］，bj为节点 j高斯基函数宽度。θ=［θ1，θ2，…θm］为网络权值向量，网络的输出为 y（t）=θTh=θ1h1+θ2h2+…+θmhm。

3.2 系统RBF神经网络补偿

针对普通的计算力矩控制策略无法实现准确跟踪问题，作出对系统建模误差进行补偿的研究，提出基于在线学习的RBF神经网络补偿的控制策略。计算力矩策略作为主体，保证系统的稳定性，同时RBF网络在线学习优化权值，不断逼近模型不确定性。控制系统的框图，如图1所示。

图1 控制系统框图Fig．1 The Control System Diagram

设计的网络输入层为三个驱动关节的角度误差及其导数，包含6个神经元；隐层包含5个节点；输出层为三个驱动臂的转矩补偿值。根据式（3），不确定性会影响控制精度，需要RBF网络在线自适应逼近系统的不确定性 f=M^-1（ΔMα¨+ΔCα˙+ΔN-τ），从

d而实现对系统不确定性的在线补偿。在线补偿过程中，RBF网络在机器人末端轨迹实时跟踪过程中被训练，根据轨迹位置和速度误差在线修正网络权值，不断逼近最佳输出，避免了RBF网络的离线训练过程。令fi表示RBF网络的最佳输出，θi表示对f最佳辨识的网络权值，则fi=θTih。令fe表示网络的实际输出，θe表示实际网络权值，则f=θTh。由文献[8]可知，网络的建模误差有界，其上

ee加入RBF网络在线补偿的控制律为：

不妨令 τ1＝M^（α）（α¨d+Kpe+Kde˙）+C^（α，α˙）α˙+N^（α），τ2=M（α）fe，则 τ＝τ1+τ2。τ1表示计算力矩控制部分，τ2表示 RBF 网络不确定性补偿部分。将RBF网络在线补偿控制律代入式（1）整理得：

3.3 系统稳定性分析及权值自适应律推导

令 x=［e，e˙］T，那么可以将式（5）转化为

4 联合仿真与结果分析

验证RBF网络在线补偿控制策略的准确性，对比不同策略下的控制效果。对Delta并联机器人进行Simulink/Simmechanics联合仿真分析。在Simulink中设计系统控制器，在Simmechanics中建立机构虚拟物理模型，把Simmechanics虚拟样机作为控制对象，通过接收驱动力矩和反馈旋转速度、加速度，进行数据交互，完成系统联合仿真。

4.1 联合仿真模型建立

Simmechanics是Matlab中根据物理结构进行建模的插件[10]，在Simmechanics中进行机器人模型的建立。模块化和图形化的建模方式使得模型结构简洁，同时在Matlab主界面可以直接观察机构的运动画面，实时了解轨迹跟踪效果，有利于控制器的改进，是一种快捷且高效的辅助动力学分析方法。Delta机器人的物理模型，如图2所示。

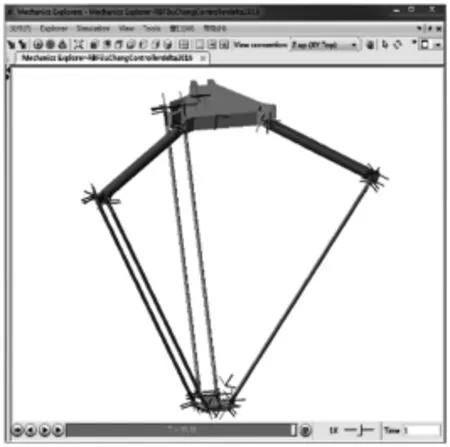
图2 Delta机器人Simmechanics模型Fig．2 The Simmechanics Model of Delta Robot

Simmechanics中的Delta并联机器人虚拟样机是一个四面体结构，有三条相同的对称布置支链。由于其支链的平行四边形结构，Delta机器人只能在一定空间范围内平动。定义机器人各铰链之间的约束关系，使其真实的模拟机构的运动状态。根据控制策略，在Simulink中建立系统控制器，输出驱动力矩信号，驱动机器人末端动平台跟踪期望轨迹，Simmechanics实时检测并反馈机器人的速度和加速度信息到系统控制器，实现联合仿真。

4.2 结果与分析

选择末端动平台的跟踪轨迹为半径50mm的圆，Z方向保持高度恒定。选取平台初始位置为（0.01，0.04，0.82），三个驱动臂初始角速度为0。Delta机器人系统动力学模型如式（2），具体表述如下：

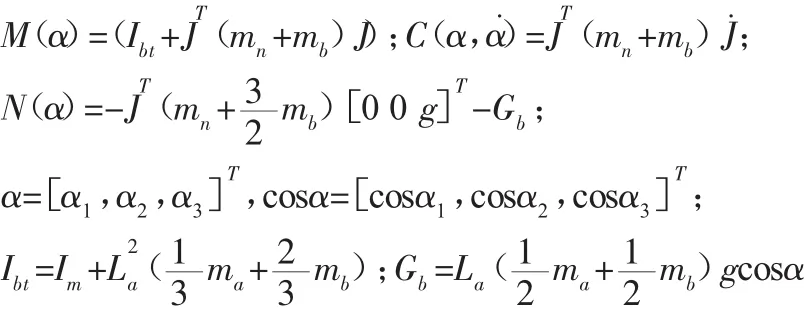
式中：E—单位矩阵；J—速度雅克比矩阵。M（α），C（α，α˙），N（α）—质量矩阵分项、向心力分项和重力分项。

在仿真模型中，选取机器人的结构参数，如表1所示。

表1 Delta并联机器人结构参数Tab.1 Parameters of the Delta Parallel Manipulator

运用Matlab/Simulink中S-Function实现对RBF补偿控制律的描述，用Matlab/Simmechanics描述被控对象。选取系统外部扰动为 τd=0.05+0.03*norm（e）+0.06*norm（e˙）。RBF 网络的输入为关节角度误差状态变量（x=［eT，e˙T］T）；隐层节点数为 5；节点中心［-0.04-0.02 0-0.02-0.04］；节点基宽度d=3；各节点初始权重取值0。分别在无外部扰动和有扰动两种情况下进行计算力矩控制和RBF神经网络在线补偿控制算法对比，仿真结果，如图5、图6所示。仿真结果如图，从图3可以看出，在外部扰动为零时，计算力矩控制策略和RBF神经网络在线补偿控制策略都能较好的跟踪期望轨迹，保障系统的稳定性。在加入外部扰动后，运动平台轨迹跟踪，如图 4（a）、图 4（b）所示。根据式（5），计算力矩控制策略稳态误差不能收敛到0，因此不能很好的跟踪末端平台期望轨迹。对于RBF网络在线补偿控制，在系统仿真开始阶段由于网络在线学习自适应调整网络权值，系统存在一定的波动。在权值逐渐逼近最优值时，跟踪效果明显好于一般的计算力矩控制策略，响应快速且稳定，具有较强的鲁棒性。为更加直观的对比仿真结果，分别给出在外部有界不确定扰动环境下X和Y方向的跟踪误差，如图5、图6所示。可以看出，计算力矩算法在系统稳定后误差不能收敛为0且误差波动幅度较大，而采用RBF在线补偿控制律的控制效果明显优于计算力矩控制，在线学习得到最佳网络权值后，系统稳定且末端动平台轨迹误差的绝对值小于0.5mm，能够很好的根据期望轨迹运动。

图3 无扰动环境下轨迹跟踪Fig.3 Trajectory Tracking without Disturbance

图4 有扰动环境下Y方向轨迹跟踪Fig.4 Trajectory Tracking with Disturbance

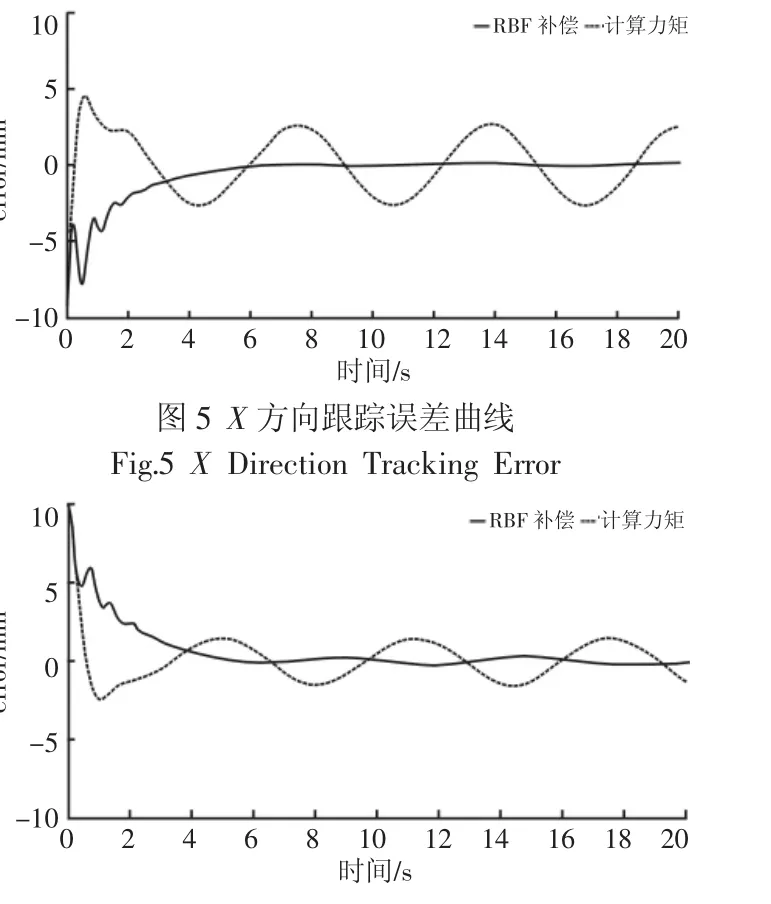
图6 Y方向跟踪误差曲线Fig.6 Y Direction Tracking Error

5 结论

针对Delta并联机器人控制过程中外部有界扰动、建模不准确等不可避免的不确定因素，结合计算力矩控制策略和RBF神经网络在线补偿控制策略，提出了一种基于计算力矩法的RBF神经网络在线补偿控制策略。采用RBF神经网络在线调整隐层网络权值，不断逼近系统不确定项，并用Lyapunov理论证明系统稳定性及推导权值自适应律。根据给定的期望轨迹和机构参数，基于Simulink、Simmechanics建立Delta机器人控制系统联合仿真模型。由仿真结果可以看出的控制策略可以很好的实现对目标轨迹的实时跟踪，控制效果优于计算力矩控制，能够有效保证Delta机器人系统稳定运行且稳态误差小，较好的提升了系统的性能。

［1］宫赤坤，蓝黎恩．Delta并联机器人的动力学研究［J］．机械科学与技术，2013（12）：1780-1784．（Gong Chi-kun，Lan Li-en．Study on the dynamics analysis of delta parallel robot［J］．Mechanical ScienceandTechnology，2013（12）：1780-1784．）

［2］申铁龙．机器人鲁棒控制基础［M］．北京：清华大学出版社，2000．（Shen Tie-long．Robust Control of Robot［M］．Beijing：Tsinghua University Press，2000．）

［3］杨晓钧，龙亿．计算力矩法的CMAC同步轨迹跟踪控制与仿真［J］．哈尔滨工业大学学报，2013（7）：85-89．（Yang Xiao-jun，Long Yi．Synchronous trajectory tracking control and simulation of CMAC neural network based on computed torque control［J］．Journal of Harbin Institute of Technology，2013（7）：85-89．）

［4］贺红林，何文丛，刘文光．神经网络与计算力矩复合的机器人运动轨迹跟踪控制［J］．农业机械学报，2013（5）：270-275．（He Hong-lin，He Wen-cong，Liu Wen-guang．Tracking control of robot using hybrid controller based on neural network and computed torque［J］．Transactions of the Chinese Society for Agricultural Machinery，2013（5）：270-275．）

［5］Linda O，Manic M．Evaluating uncertainty resiliency of type2 fuzzy logic controllers for parallel Delta robot［C］．IEEE 4thInternational Conference on Human System Interactions．Piscataway，USA：IEEE，201（5）：91-97．

［6］江道根，高国琴，胡红玉．六自由度并联机器人线性化反馈RBF神经滑模控制研究［J］．机械设计与制造，2010（2）：159-161．（Jiang Dao-gen，Gao Guo-qin，Hu Hong-yu．The study on parallel robot of RBF netrual sliding controller［J］．Machinery Design&Manufacture，2010（2）：159-161．）

［7］ParkJ，SandbergLW．Universalapproximationusingradial-basis-function networks［J］．Neutral Comput，1991，3（2）：246-257．

［8］刘金琨．机器人控制系统的设计与MATLAB仿真［M］．北京：清华大学出版社，2008．（Liu Jin-kun．Design and MATLAB Simulation of Roboticsystems［M］．Beijing：Tsinghua University Press，2008．）

［9］KatsuhikoOgata．ModernControlEngineering［M］．USA：PrenticeHall，2007．

［10］王英波，黄其涛，郑书涛．Simulink和SimMechanics环境下并联机器人动力学建模与分析［J］．哈尔滨工程大学学报，2012（1）：100-105．（Wang Ying-bo，Huang Qi-tao，Zheng Shu-tao．Dynamic modeling and analysis of a parallel manipulator using Simulink and SimMechanics［J］．Journal of Harbin Enginering University，2012（1）：100-105．）