基于多因子交互作用的PP/EPDM复合材料注射成型工艺优化
2018-03-22旭林
,旭林,, ,,,
(1.宁夏大学机械工程学院,银川 750021;2.湖南大学,汽车车身先进设计制造国家重点实验室,长沙 410082; 3.大连理工大学机械工程学院,大连 116023)
0 引 言
注射成型是一种重要的塑料制品加工方式,适用于形状复杂、尺寸精度高的塑料制品的大批量生产[1]。早在20世纪70年代初期,研究者就开始对注射成型过程的仿真开展了相关研究[2-4]。随着计算机技术和计算力学、流体力学、聚合物加工流变学、传热学等学科的发展,注射成型工艺优化的数值模拟研究受到了国内外学者的广泛关注。SEOW等[5]采用自动壁厚更新技术,对简单注塑件的流场进行了优化。YAMAKAWA等[6]基于改进的网格模型,模拟了塑料熔体在任意形状薄壁型腔中的流动。GUPTA[7]基于伽辽金法,模拟了三维薄壁件的注塑成型过程,优化了流动前沿位置。戴亚春等[8]、王善凯等[9]、刘色荣等[10]、刘朝福等[11]基于正交试验设计方法,研究了注射温度、模具温度、注射时间、保压时间等工艺参数对注射制品翘曲变形量的影响,获得了最优的注射成型工艺参数。党玉春等[12]采用析因设计方法,从众多的试验因子中筛选出与注射制品质量密切相关的若干独立因子和交互因子,并在此基础上通过正交试验得到最优的工艺参数组合;林权[13]对注塑件成型后的体积收缩率、翘曲变形量和表面气穴等3个目标值进行综合评判,通过对工艺参数的极差分析确定了最优的工艺参数组合。上述工作主要研究了工艺参数主因子和交互因子对单目标的影响,以及工艺参数主因子对多目标值的影响,而有关工艺参数交互因子对多目标值影响的研究较少。在注射成型过程中,注射制品的质量不仅受单因子的影响,还受到多因子交互作用的影响,这增加了工艺条件与制品性能分析的难度。
为此,作者以汽车侧踏板聚丙烯/三元乙丙烯(PP/EPDM)复合材料端盖为研究对象,基于Moldflow软件建立注射成型仿真模型,以工件翘曲量、体积收缩率及表面缩痕指数最小化为目标,通过析因设计筛选出对目标值影响显著的工艺参数主因子及交互因子,结合正交试验设计方法模拟得到最佳工艺,并进行验证。
1 有限元模拟
1.1 模型的建立
汽车侧踏板端盖外形尺寸为长155.5 mm、宽143.6 mm、高83.2 mm,筋板壁厚为1.0 mm,外壳壁厚为2.5~3.0 mm,其三维模型如图1(a)所示。利用Moldflow仿真软件,采用双层面网格进行单元划分,并按照实际模具结构采用一模两腔模型,建立侧浇口、主流道、分流道和冷凝管道,冷凝管道中的冷却介质为25 ℃的水,冷却介质雷诺数为10 000,以确保冷却介质处于湍流状态。注射成型模具及有限元模型如图1(b)~(c)所示,其中三角形单元数量为35 317个,节点数为17 498个,最大纵横比5.9,网格匹配率92.3%。
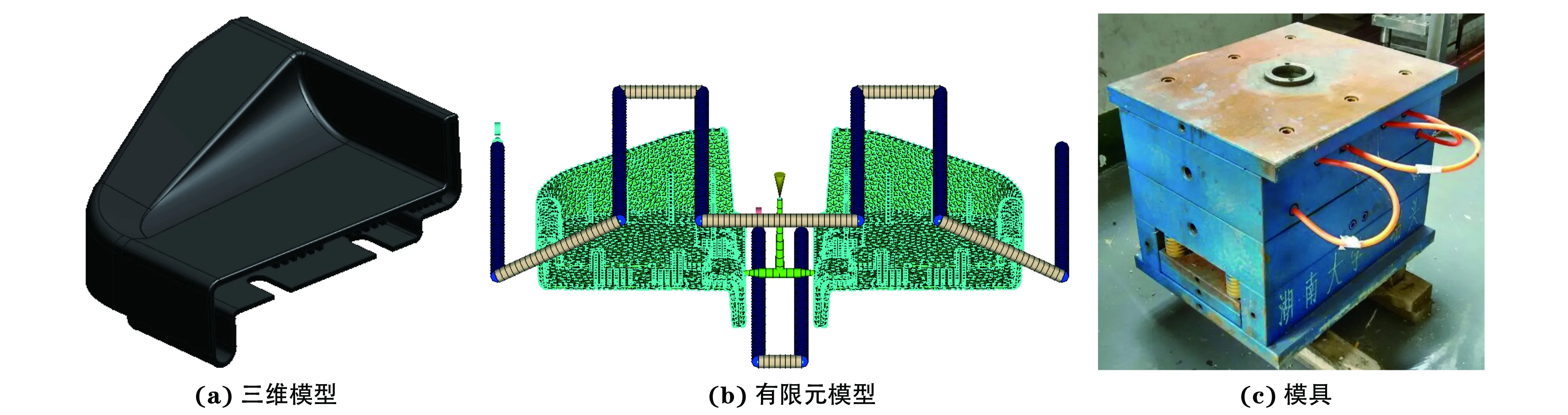
图1 汽车脚踏板盖板的三维模型、注射成型有限元模型及模具Fig.1 Three-dimensional model (a), finite element model (b) and mold (c) of injection molding of automobile footboard cover
1.2 注射成型模拟参数
汽车侧踏板端盖材料采用聚丙烯/三元乙丙烯复合材料,其主要注射成型模拟参数如表1所示。图2为Moldflow塑料实验室采用间接膨胀方法测试的PVT曲线和剪切应变速率-黏度曲线,图中P为注射压力,T为熔体温度。由图2可知:随着熔体温度的升高或注射压力的减小,复合材料的比体积逐渐增加;复合材料的黏度随熔体温度的降低与剪切应变速率的增大而逐渐减小。
1.3 模拟结果及分析
原工艺方案的注射压力为180 MPa、熔体温度为220 ℃、模具温度为35 ℃、注射时间为1.8 s、冷却时间为18.5 s、保压时间为10 s、保压压力为填充压力的80%,模拟得到该工艺方案下注射成型后端盖的翘曲量分布和流动前沿温度分布,并与实际注射件进行了对比。

表1 聚丙烯/三元乙丙烯复合材料注射成型模拟参数Tab.1 Simulation parameters of injection molding of PP/EPDM composite
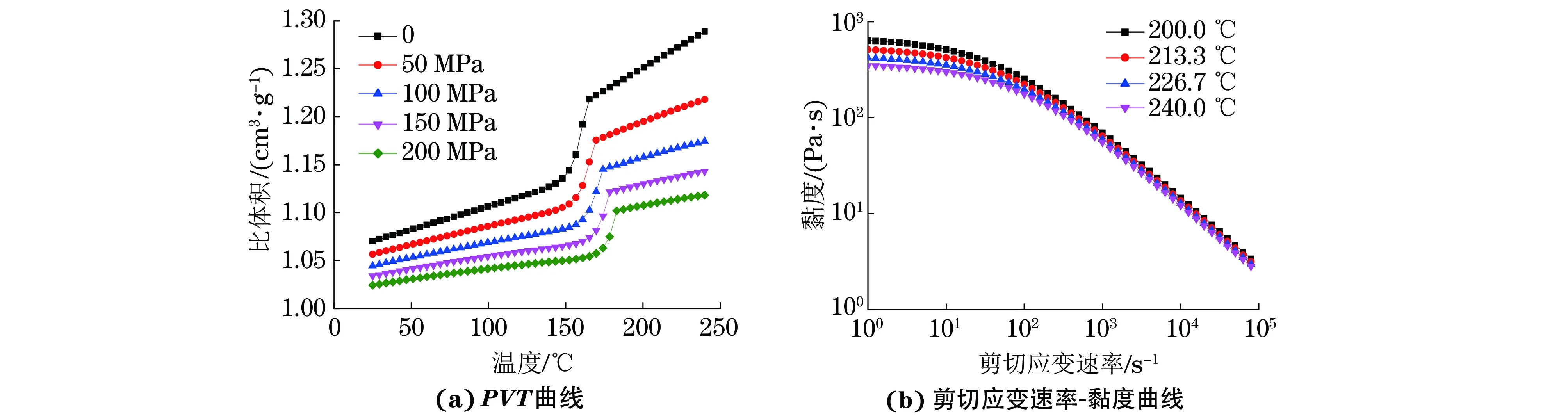
图2 PP/EPDM复合材料的PVT曲线和剪切应变速率-黏度曲线Fig.2 PVT curves (a) and shear strain rate-viscosity curves (b) of PP/EPDM composite
图3(a)为数值模拟得到的汽车脚踏板盖板节点位移云图,其中浅色透明部分为标准尺寸模型,彩色部分为模拟得到变形的注射件模型,可以发现圆圈区域的卡扣平面向上发生翘曲变形,左侧翘曲量为1.51 mm,右侧为1.31 mm;图3(b)为相同工艺参数下实际注射件,可以发现卡扣位置存在明显的不均匀变形,且左侧变形量大于右侧的。
图4(a)为数值模拟得到的汽车脚踏板盖板在熔体充填过程中的流动前沿温度云图,可以发现在熔体充填过程中,蓝色区域温度较低,梯度温度导致熔体冷却速率不一致,凝固时发生不均匀收缩,从而产生拉伸变形,形成残余拉应力并最终导致开裂。由图4(b)~(c)可知,实际注射件在相同位置出现了可见裂纹。
综上所述,翘曲变形和冷却收缩的模拟结果与实际注射件的一致,这说明所建立的有限元模型可靠,能够较准确地预测注射成型过程中端盖的翘曲变形,可用于后续的工艺优化。
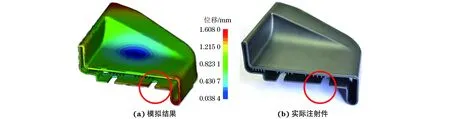
图3 汽车脚踏板盖板翘曲量模拟结果与实际注射件的对比Fig.3 Comparison between simulation results of warpage of automobile footboard cover (a) and the actual injection molded part (b)

图4 汽车脚踏板盖板流动前沿温度模拟结果与实际注射件的对比Fig.4 Comparison between simulation results of flow front temperature of automobile footboard cover (a) and the actual injection molded part: (b) overall morphology of actual injection molded part and (c) local amplification of actual injection molded part
2 基于析因设计的影响因子分析
2.1 因子与水平
根据注射件的推荐工艺、成型窗口分析以及相关文献[14]设计其因子水平表,如表2所示。
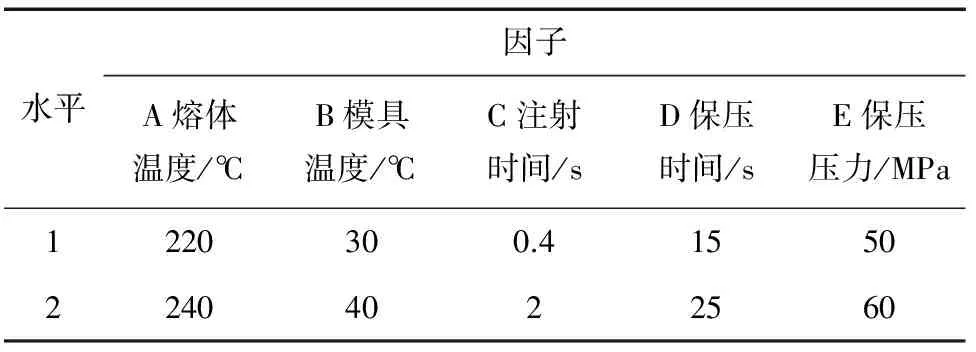
表2 注射成型工艺参数的因子和水平Tab.2 Factors and levels of injection moldingprocess parameters
2.2 部分因子模拟结果分析
为了探明主因子及其交互因子对最大翘曲量、体积收缩率、表面缩痕指数的影响,需要采用试验设计(DOE)方法进行部分因子试验,采用上述已验证的有限元模型进行16组试验,所得到的模拟结果如表3所示。
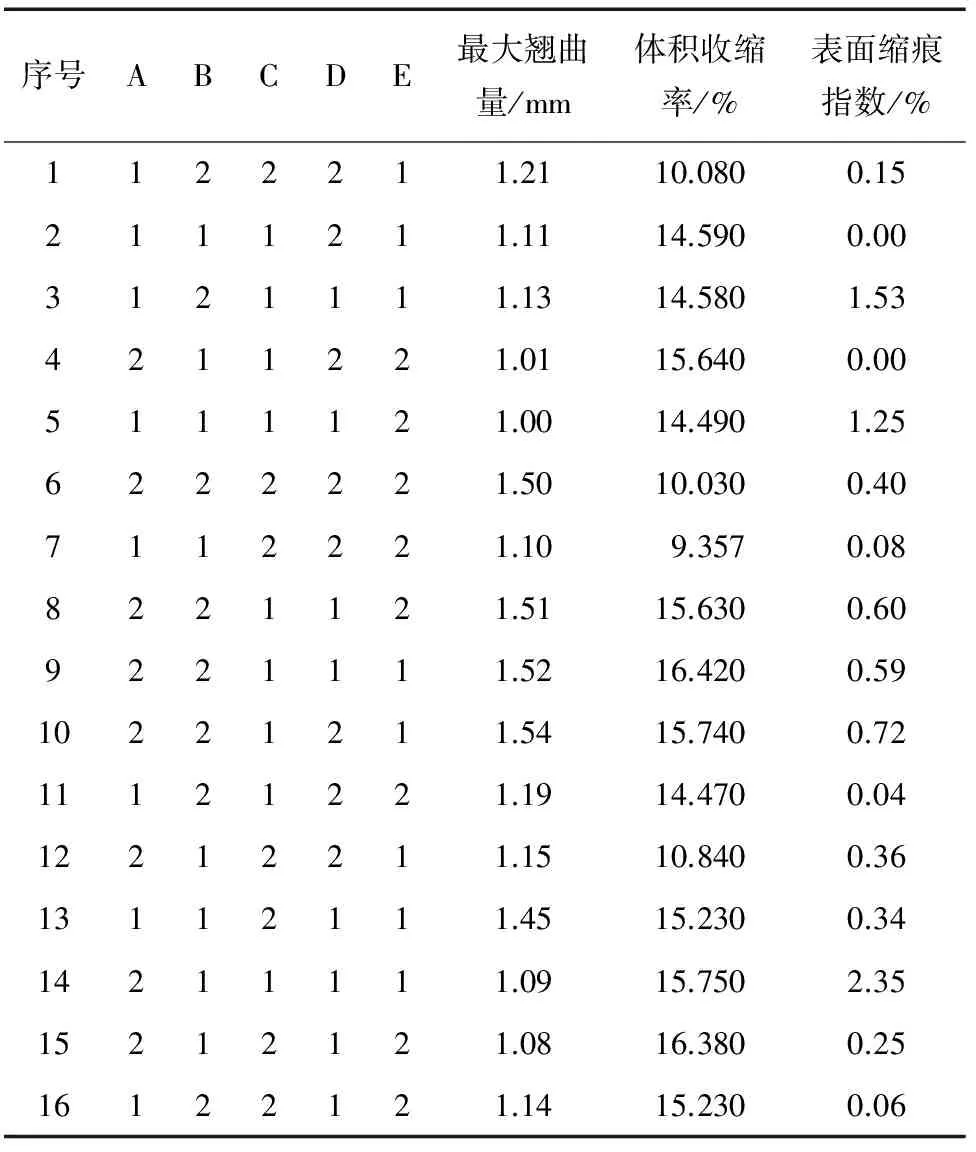
表3 部分因子试验方案及模拟结果Tab.3 Experiment design and simulation results ofpartial factors
2.3 交互作用分析
根据统计学抽样分布原理,该试验总体容量为32,从中随机抽取16组进行试验,因样本容量较少,采用正态分布抽样会带来较大的误差,所以应采用t分布近似处理[15],其统计量公式为
(1)
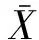
图5为基于式(1)计算得到的不同目标值(最大翘曲量、体积收缩率、表面缩痕指数)的排列示意,其中只考虑二阶因子的交互作用,并将单因子的主效应和因子之间的交互作用以降序方式排列。
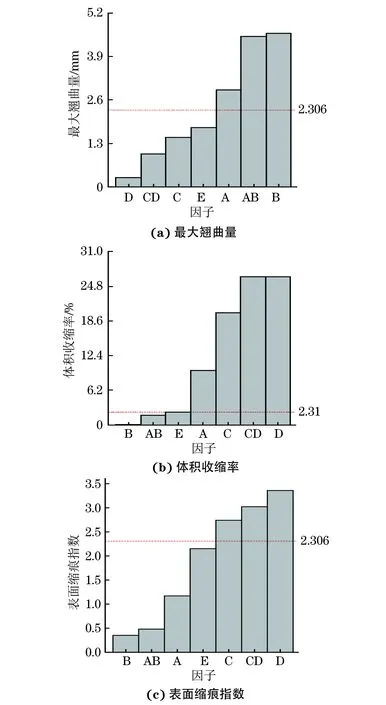
图5 单因子与交互因子影响的不同目标值的排列示意Fig.5 Permutation diagrams of individual factor and interaction factor influence on different object values: (a) maximum warpage; (b) volume shrinkage and (c) surface sink marks index
由图5可知:对于最大翘曲量,单因子A,B,交互因子AB的t值分别为2.90,4.61,4.51,分别超出其临界值0.59,2.30,2.20,因此影响最大翘曲量的主要单因子为熔体温度和模具温度,交互因子为AB;对于体积收缩率,单因子A,C,D,E和交互因子CD的t值分别超出其临界值7.41,17.73,24.25,0.01,24.23,因此影响体积收缩率的主要单因子为熔体温度、注射时间、保压时间、保压压力,交互因子为CD;对于表面缩痕指数,单因子注射时间、保压时间(分别超出其临界值0.43,1.50)以及交互因子CD(超出其临界值0.71)对表面缩痕指数的影响显著。综上所述,交互因子对各目标均有显著的影响,A,B,C,D,E为对目标影响显著的工艺参数主因子,AB和CD为对目标影响显著的工艺参数交互因子。
3 基于正交试验设计的工艺参数优化
3.1 因子水平设计
由部分因子试验可知,交互因子对各目标值均有显著影响,在设计正交试验方案时必须考虑其影响,以获得更加准确的试验结果。正交试验中因素水平表与部分因子试验的相同,如表2所示,表中的因子即为因素。为了避免因子与因子、因子与交互因子以及交互因子之间的混杂,采用L16正交矩阵[16]。表4为正交试验方案及模拟结果,其中e表示空列。
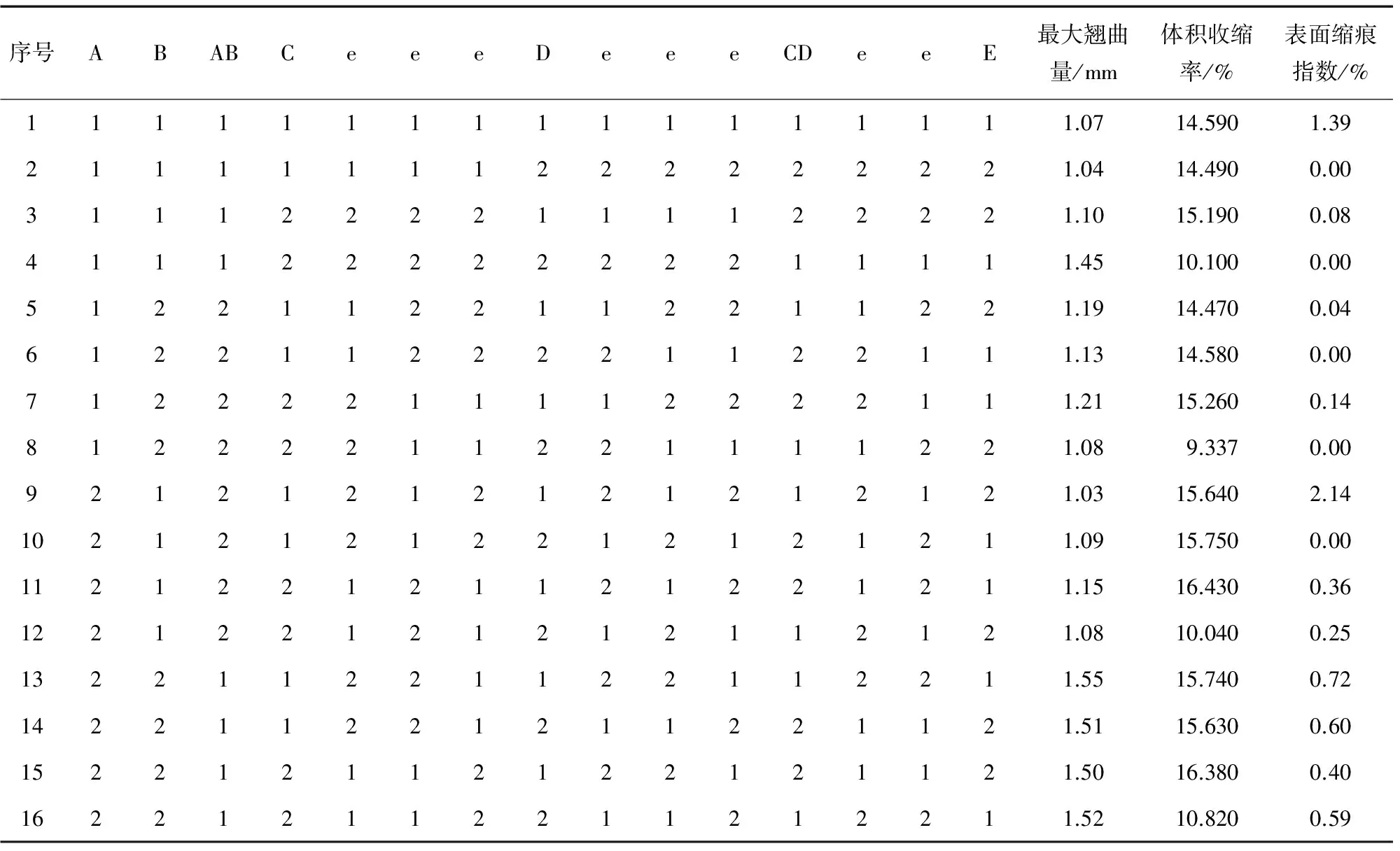
表4 正交试验方案及模拟结果Tab.4 Experiment design and simulation results of orthogonal test
3.2 正交试验结果分析
采用信噪比S/N研究各水平对目标值的影响,分别计算出不同水平目标值的信噪比,并将其作为衡量因子重要性的指标,信噪比越大表示因子对目标值的敏感程度越小。为了使注射件获得更好的质量,需保证各目标值最小,因此引入望小特性的信噪比,即信噪比越大,各目标值就越小,注射件质量越好,其计算公式为
(2)
式中:yi为第i次试验的目标值;n为试验方案次数。
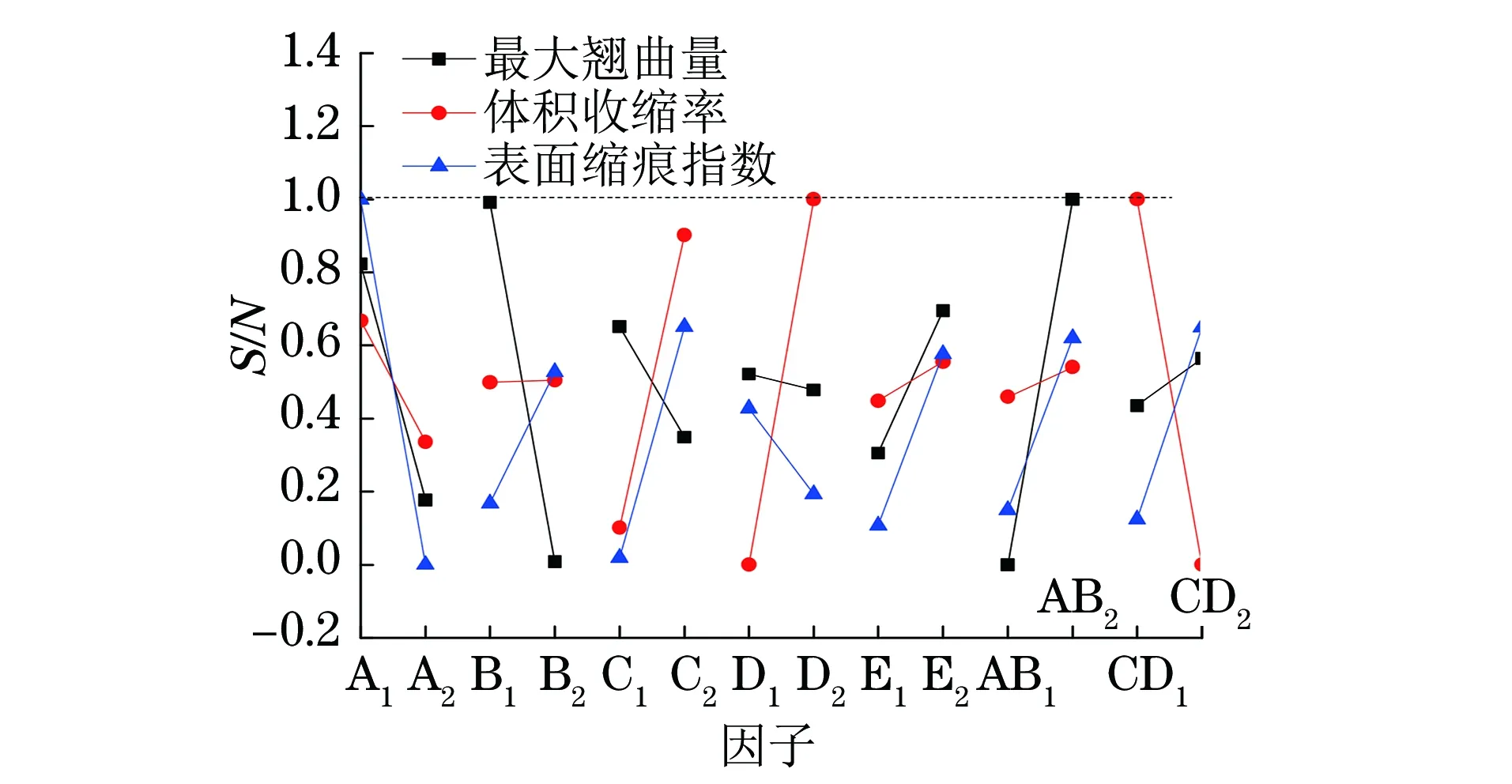
图6 目标值的信噪比分析Fig.6 Analysis of signal-to-noise ratio of object values
计算出各目标值的信噪比后进行归一化处理,如图6所示。由图6可以看出:某些交互因子对目标值的影响大于单因子的。但是该图仅适用于单因子最优方案的分析,因此需要进一步研究交互因子对目标值的影响。
对于最大翘曲量:交互因子AB对最大翘曲量的影响程度最大,如图6所示,因此根据表5,交互因子取A2B1;若仅考虑单因子C,D的影响,取C1和D1为最优方案,但交互因子CD的影响大于单因子D的,如图6所示,因此由表5可得最优方案为C1D2。综上所述,其最优方案为A2B1C1D2E2。
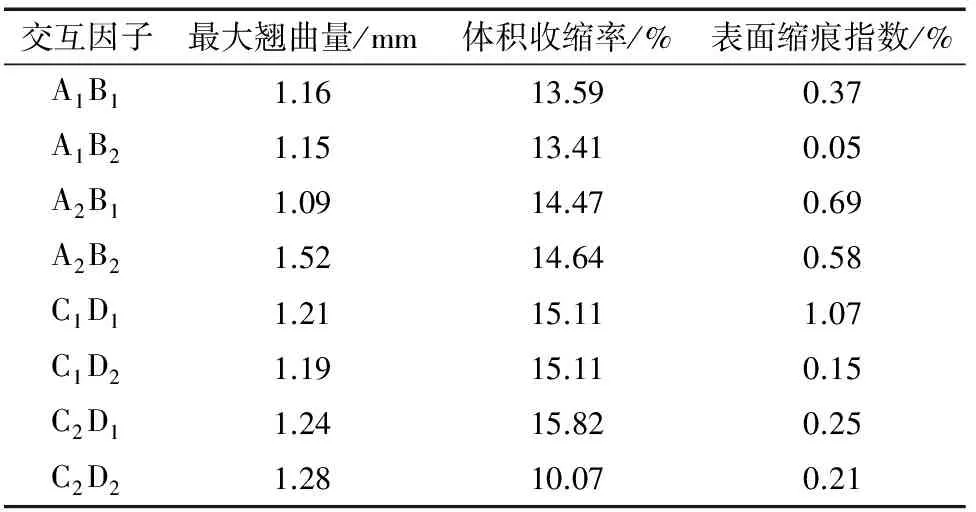
表5 交互因子的目标均值Tab.5 Average object values of interaction factors
对于体积收缩率:交互因子CD的影响程度最大,如图6所示,因此根据表5,交互因子取C2D2;若仅考虑A,B单因子的影响,A1和B2为最优方案,但交互因子AB的影响大于B的,如图6所示,因此由表5可得最优方案为A1B2。综上所述,其最优方案为A1B2C2D2E2。
对于表面缩痕指数:单因子A的影响程度最大,C次之,因此由图6可得A1和C2为最优方案;若仅考虑单因子的影响,B2和D1为最优方案,但交互因子AB和CD的影响程度大于单因子B的和D的,因此由表5可得最优方案为B2和D2。综上所述,其最优方案为A1B2C2D2E2。
由上述模拟结果并根据综合平衡法可得,PP/EPDM复合材料注射成型工艺的最优方案为A1B2C2D2E2,即当熔体温度为220 ℃、模具温度为40 ℃、注射时间为2.0 s、保压时间为25 s、保压压力为60 MPa时,注射件的质量最优。
4 优化工艺验证
由图7可知,在优化工艺下模拟得到的注射件位移场分布更加均匀,卡扣平面的变形减小,卡扣处左右翘曲量的差值由0.65 mm减小为0.05 mm。这是由于模具温度由35 ℃升高到40 ℃后,减少了注射件的内应力和聚合物分子的取向度,同时注射时间由1.8 s延长至2 s后,更多的塑料熔体进入型腔中,起到了补缩的作用,从而减小了翘曲量。
由图8可知:在原工艺方案下模拟得到注射件不同位置的体积收缩率相差较大,最大体积收缩率为8.38%,最小体积收缩率为1.61%,相差6.77%;在优化工艺下,体积收缩率分布均匀,最大体积收缩率为2.23%,最小收缩率为1.00%,两者相差仅1.23%,体积收缩率变化很小。这是由于保压时间由10 s延长至25 s后,改善了浇口附近由于温度不均而产生的内应力。同时,保压压力由144 MPa降到60 MPa后,提高了注射件的表面质量并能够有效防止注射件过分收缩。
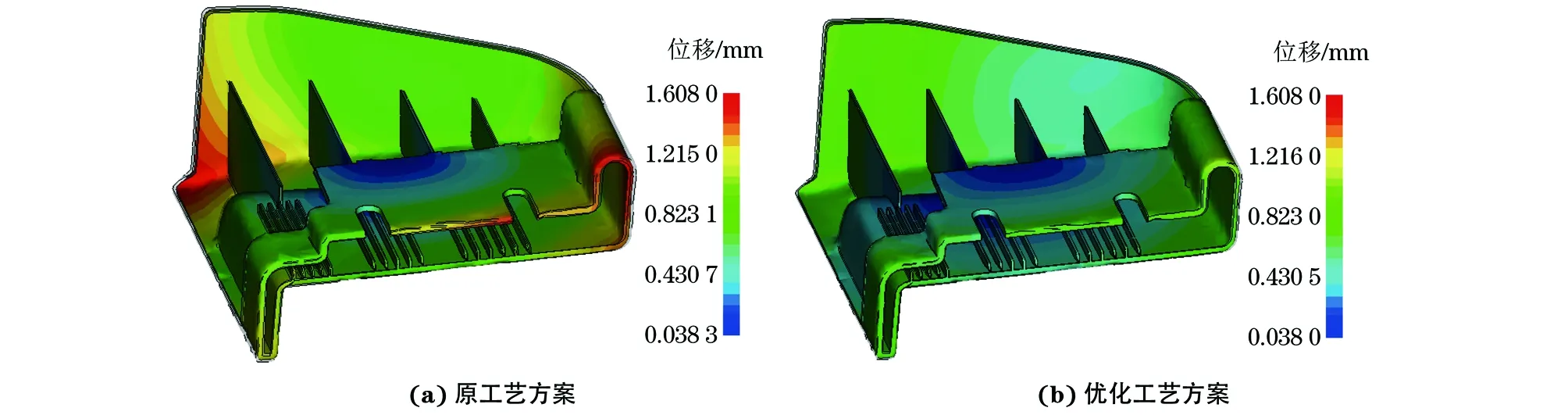
图7 在原工艺方案与优化工艺方案下模拟得到注射件的翘曲量分布Fig.7 Simulated warpage distribution of the injection molded part with the original (a) and the optimal process (b)
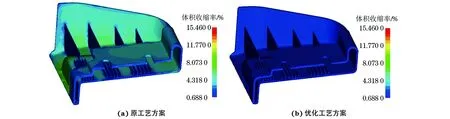
图8 在原工艺方案与优化工艺方案下模拟得到注射件的体积收缩率分布Fig.8 Simulated volume shrinkage distribution of the injection molded part with original (a) and the optimal process (b)
由图9可知:在原工艺方案下模拟得到的注射件浇口附近存在缩痕;在优化工艺方案下,注射时间的延长使塑料熔体对缩痕处进行充分补缩,保压时间的适当延长防止了注射件收缩,模具温度的提高改善了表面粗糙度,从而使表面缩痕消失。
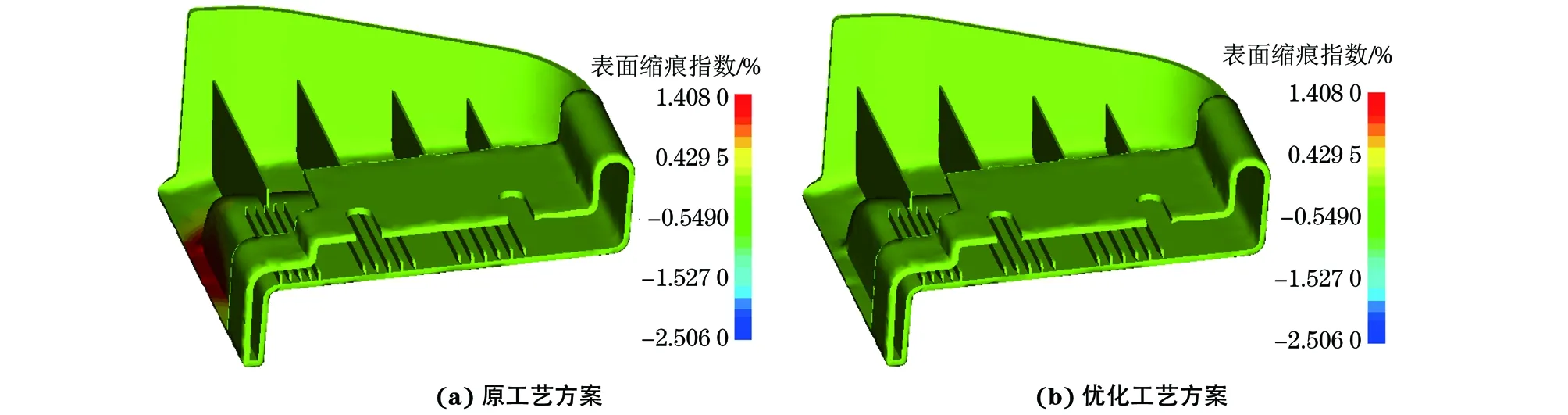
图9 采用原工艺方案与优化工艺方案模拟得到注射件的表面缩痕指数分布Fig.9 Simulated surface sink mark index distribution of the injection molded part with original (a) and the optimal process (b)
由图10可以看出:与采用原工艺方案相比(见图4),优化工艺方案下模拟得到的注射件的温度分布更加均匀,消除了加强筋处由于收缩不均匀而产生的残余拉应力,显著降低了裂纹产生的概率。
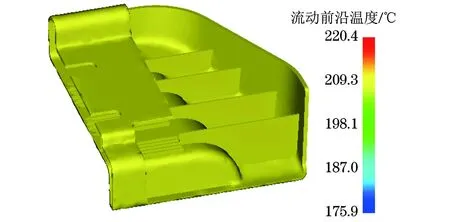
图10 优化工艺下模拟得到注射件的流动前沿温度分布Fig.10 Simulated flow front temperature distribution of the injection molded part with the optimal process
模拟结果表明:工艺优化后注射件的最大翘曲量为1.07 mm,与原工艺方案的(1.61 mm)相比,减小了33.21%;优化后其体积收缩率为9.34%,与原工艺方案的(15.46%)相比,下降了39.61%;优化后其表面缩痕指数为0,消除了表面缩痕,工件的质量显著提高。采用优化后的工艺进行试制,得到的注射件如图11所示,可以看出其卡扣平面处的翘曲减小,注射件表面平整光滑,无裂纹等加工缺陷,质量显著提高,与模拟结果一致。

图11 采用优化工艺注射成型后端盖的外观形貌Fig.11 Appearance of the end cap after injection molding with the optimal process
5 结 论
(1) 采用有限元模型模拟汽车侧踏板端盖的注射成型,模拟得到注射件的翘曲和冷却收缩结果与实际注射件的一致,验证了该模型的准确性。
(2) 基于析因设计得到对目标值影响显著的主因子为熔体温度、模具温度、注射时间、保压时间和保压压力,交互因子为熔体温度与模具温度、注射时间与保压时间。
(3) 最优注射成型工艺为熔体温度220 ℃、模具温度40 ℃、注射时间2.0 s、保压时间25 s、保压压力60 MPa,模拟得到端盖的最大翘曲量比原工艺方案的减小了33.21%,体积收缩率降低了39.61%,表面质量显著提高。
[1] 张志莲, 江波. 注射成型工艺参数之间的交互作用[J]. 化工学报, 2006, 57(2):448-452.
[2] HARRY D H, PARROTT R G, HARRY D H,etal. Numerical simulation of injection mold filling[J]. Polymer Engineering & Science, 1970, 10(10):209-214.
[3] TADMOR Z, BROYER E C, GUTFINGER C. Flow analysis network—A method for solving flow problem in polymer processing[J]. Polymer Engineering & Science, 1974, 14(9):660-665.
[4] HIEBER C A, SHEN S F. A finite-element/finite-difference simulation of the injection-molding filling process[J]. Journal of Non-Newtonian Fluid Mechanics, 1980, 7(1):1-32.
[5] SEOW L W, LAM Y C. Optimizing flow in plastic injection molding[J]. Journal of Materials Processing Technology, 1997, 72(3):333-341.
[6] YAMAKAWA S, SHAW C, SHIMADA K. Layered tetrahedral meshing of thin-walled solids for plastic injection molding FEM[J]. Computer-Aided Design, 2005, 38(4):245-255.
[7] GUPTA A, KELLY P. Optimal galerkin finite element methods for non-isothermal liquid composite moulding process simulations[J]. International Journal of Heat & Mass Transfer, 2013, 64:609-622.
[8] 戴亚春, 王匀, 周建忠, 等. 微齿轮注塑成型正交优化及数值模拟[J]. 材料工程, 2010(7):46-48.
[9] 王善凯, 李晶, 胡激涛, 等. 基于Moldflow汽车配件注塑工艺参数优化[J]. 西安工程大学学报, 2015, 29(6):692-697.
[10] 刘色容, 林有希, 卢月美, 等. 工艺参数对模内覆模注塑件翘曲变形的影响[J]. 工程塑料应用, 2015, 43(7):46-51.
[11] 刘朝福, 刘建伟, 何玉林. 基于正交试验的PP车门内饰板注塑工艺参数优化[J]. 合成树脂及塑料, 2015, 32(1):50-53.
[12] 党玉春, 丁清国, 刘泓滨. 基于DOE因子交互作用的注射成型工艺参数优化研究[J]. 新技术新工艺, 2013 (10):75-78.
[13] 林权. 基于综合平衡法的注塑工艺参数多目标优化设计[J]. 塑料科技, 2011, 39(1):84-88.
[14] 叶久新, 王群. 塑料成型工艺及模具设计[M]. 北京: 机械工业出版社, 2008:62-63.
[15] 王首绪, 龙琰, 郭四泽. 基于t分布理论的公路定额数据小样本容量的收敛条件[J].长沙理工大学学报(自然科学版), 2007, 4(2):13-15.
[16] 张瑞江, 张业旺, 闻崇炜, 等. 正交试验设计和分析方法研究[J]. 实验技术与管理, 2010, 27(9):52-55.
