城市轨道交通骨干线路开通对票务清分影响研究

易燕妮

成都轨道交通集团有限公司，四川成都 610058

网络化运营管理条件下，客流数据的准确清分是分析网络客流分布特征、制定合理的网络运营计划、提高各线路运营协调性、发挥系统的整体能力和综合效益以及应急处置能力的重要基础[1]。

随着成都轨道交通网络化进程的快速推进，结合轨道交通网络结构的复杂性、换乘路径的多元性、客流需求时空分布特点的多重性等特征，研究骨干线路开通后新网络条件下清分模型和参数的优化，从而准确、合理地确定网络化运营条件下的客流性质、时空分布特点及规律，对于制订列车运行计划、进行合理的运能配置和运营成本控制、提高运输组织水平和客运服务水平具有极其重要的作用[2]。

1 国内轨道交通清分方法及客流分析模型

北京、上海两地的轨道交通系统建设最早、规模最大，并率先进入网络化运营管理阶段，其各自所采用的轨道交通网络清分系统在国内具有代表性。下面重点对北京、上海地铁清分情况进行介绍。

1.1 北京地铁

2008年之前，北京轨道交通系统无明显的清分模型。2008年北京奥运会之后，随着轨道交通路网呈现网络化发展、客运量不断增大、运营商多样化，北京轨道交通运营管理部门开始采用基于多路径概率选择的“两阶段、双比例”的清分模型。

2014年前后，北京轨道交通通过总结分析现有客票清算管理中心（ACC）和路网指挥调度中心（TCC）系统的技术条件、数据组成、开通运营至今所积累的大量客流基础数据及现有清分模型的客流计算结果，提出采用“推定型”清分模型计算客流分布，根据乘客的出行时间与实际列车运行图相匹配以非集计的思想对客流分布情况进行计算和统计，提升清分模型的准确性与合理性。但由于推定型模型约束较多计算复杂，在轨道交通系统进行票款清分时仍然保留了计算相对简便且同样能够保证网络整体分配可靠性的“分配型”模型。

1.2 上海地铁

上海城市轨道交通网络清分方法及模型从无到有、发展至今，主要经历了四个阶段：无清分阶段（1993-2000年）、人工分账阶段（2001-2005年）、最短路清分阶段（2006-2007年）、多路径清分阶段（2008年至今）。从2008年至今上海轨道交通采用了多路径清分模型。

上海轨道交通多路径清分模型在对网络进行描述时，需要形成综合阻抗函数以衡量各条路径的出行代价。在计算路径阻抗时要对影响乘客出行路径选择的各种因素进行综合考虑，这是由于影响乘客出行选择行为的因素众多，每条路径的代价（或者效用）都难以由单一因素衡量，因此有必要明确主影响因素，将其作为路径选择规则，并且将其他影响因素转化为与之统一的度量衡，从而形成可选路径的综合阻抗。

乘客在选择出行路径时总会按照一定的规则，如出行总里程最短、出行总时间最少、所经车站数最少、所需换乘次数最少、舒适度最好拥挤度最小等。上海现有清分模型中路阻函数是以里程为阻抗，将各项影响因子折算为里程计算路径代价。

2 成都地铁现状

成都地铁ACC清分系统支持最短路径算法、最短时间算法、多路径概率清分算法等多种算法模型。根据线网发展规划，可在不同时期、不同的网络结构特点下，选用合适的算法模型，其中多路径概率清分法即是为成网后复杂线路情况下的清分准备的，前期“基于出行距离换乘次数的权重比例法”为简化版的多路径概率清分法，仅使用较少参数参与算法计算。

骨干环线7号线开通后，“基于出行距离换乘次数的权重比例法”将不再适应新网络布局下的数据清分，有限条件下的数据清分难以迎合“井+网”状线网结构的复杂需求，有必要启用其他影响路径分配的关键要素，并在有效路径搜索过程中增加对阈值的设定，来最终确定真实反映乘客出行行为的有效路径。

3 成都地铁ACC清分算法模型和参数设置

通过横向对比，目前国内网络化运营的地铁基本采用的多路径概率清分法，诸如北京、上海、广州等地铁。多路径概率清分法考虑了乘客出行路径的多样性，确定几条乘客可能选择的合理路径，根据一定的原则确定每条路径的客流分配比例，进而结合各线路承担的运输里程计算出清分比例[3]。该算法适用于线网复杂程度高、路径选择繁复多样情况下的数据清分，能贴切展现乘客乘车路线的实际选择情况和各方收益分配，体现了更加科学、准确、客观、公平地分配客流及收益原则。

根据ACC前期系统设计及当前国内地铁清分情况，成都地铁ACC迫切需要向全面的多路径概率清分法扩展。

3.1 ACC清分算法模型

经研究及归纳总结，成都地铁多路径概率清分法主要通过以下步骤完成清分：

3.1.1 综合出行阻抗函数的建立与计算

以出行时间为标尺，把区间运行时间、停站时间、换乘走行时间、换乘放大系数通过参数标定建立综合函数关系，计算得出综合出行阻抗值。综合出行阻抗为乘客出行路径选择的主要依据，一般来说，阻抗值越小，乘客趋向于选择这条路径的意愿越强[4]；反之亦然。

3.1.2 有效路径的判断与比例计算

通过综合出行阻抗函数值，判断及筛选出最短时间路径，再根据乘客路径选择时考虑综合出行阻抗对于最短路径的相对和绝对上界，即阻抗相对阈值和阻抗绝对阈值，来确定有效路径范围，比如某个OD最短时间路径用时10min，当比最短路径多出60%的时间，或多出5min时，乘客不会选择该路径，则阻抗相对阈值为160%，阻抗绝对阈值为5，那么用时范围在10～15min的所有路径均为有效路径。

有效路径选择出来后，以各路径的综合阻抗函数值为基础，设置正态分布标准差参数的取值，按照一定的算法及概率分布模型，确定各有效路径分担某一OD客流的比例[5]。正态分布标准差参数取值越小，有效路径承担客流比例的差异程度越大，反之客流在各条有效路径间的分配越平均，该参数通过乘客调查拟合，一般取0.2～0.3。

3.1.3 线路清分比例的确定

在计算各条线路的客流及收益清分比例时，应考虑运营成本，而运营成本主要与承担的运营里程相关，因此，采用基于线路承担里程数的客流分配方法更为合理。在确定了每条有效路径的分配比例之后，通过计算每条有效路径中每条线路的分配比例，再将所有有效路径中相同线路的分配比例汇总，得到其线路在一个OD中的客流分配比例。

3.2 清分参数设置

对上述清分算法模型进行梳理，涉及的参数情况如表1所示。

表1 清分参数

区间运行时间等参数是依据特定的数据进行取值，换乘走行时间参数是通过实地测量得出，但换乘放大系数等四个参数的取值范围是通过研究和数据测算所得。

7号线开通初期，在参考其他地铁的参数设置经验基础上，根据7号线开通的路径清分结果影响及灵敏度分析，建议将换乘放大系数等四个参数按表 2取值进行系统参数设置。

表2 参数取值

根据上述取值，对各参数在ACC测试环境进行部署后，以202万的进站客流进行模拟计算，换乘系数为1.5744，客运量为318万，如表 3所示。

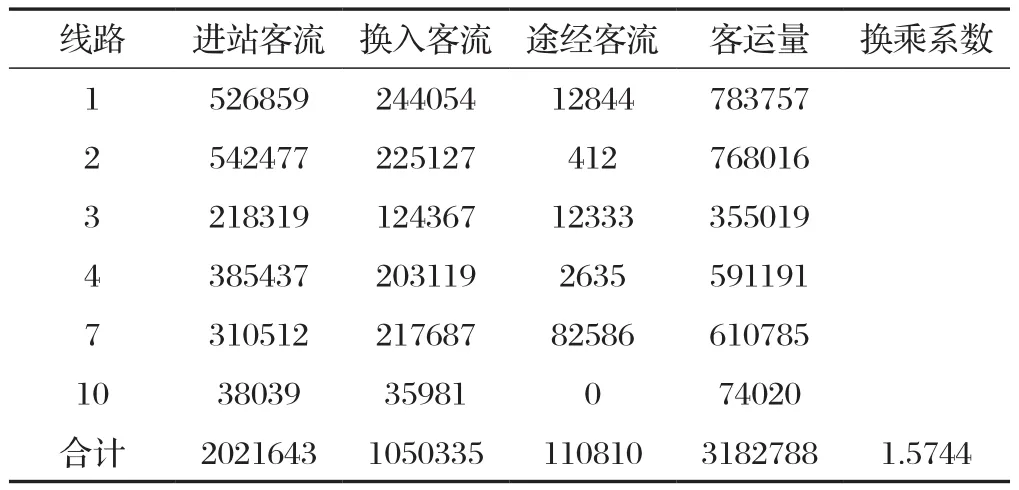
表3 换乘系数

部分OD清分比例情况列举如表 4所示。

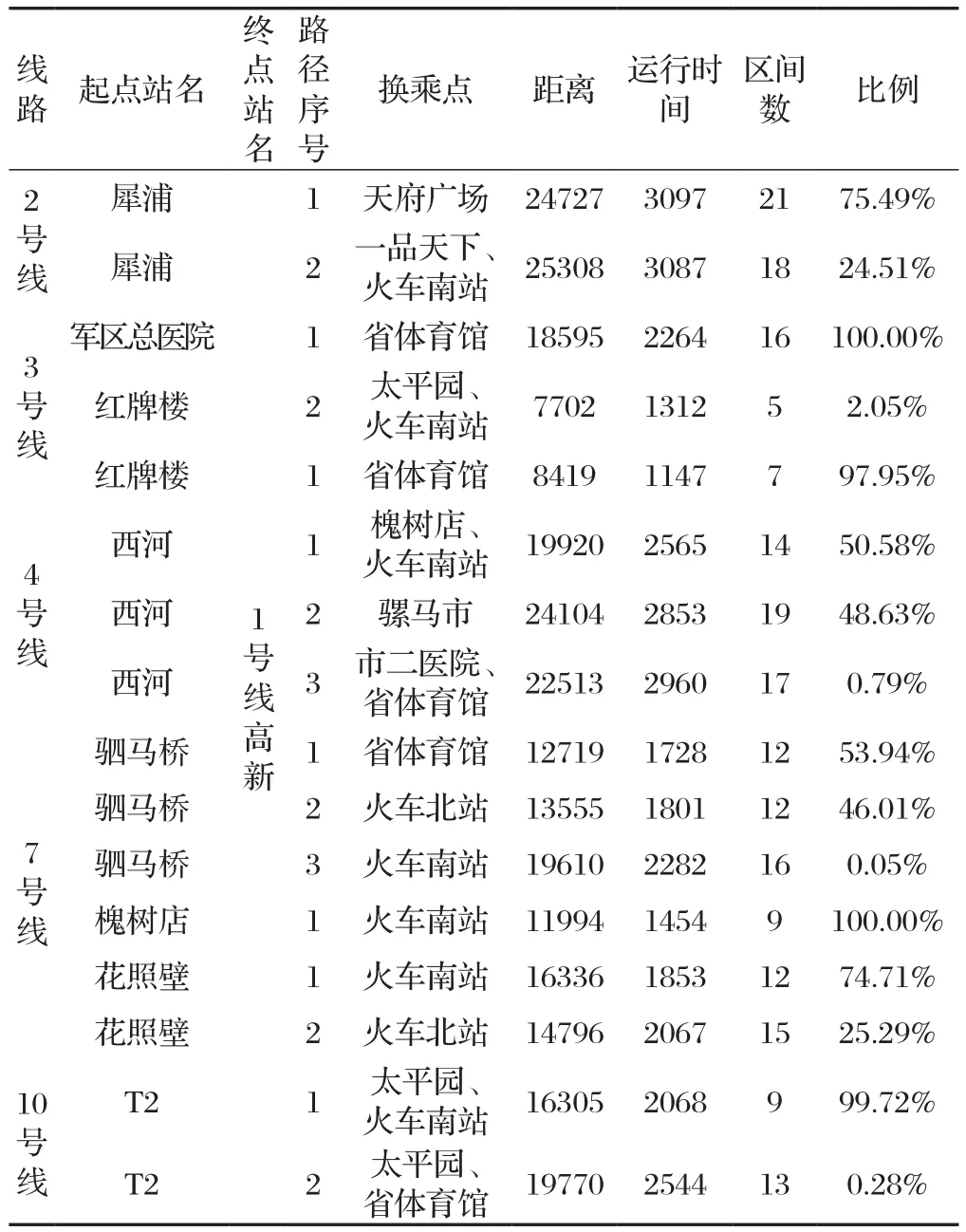
表4 部分OD清分比例

3.3 参数优化

地铁7号线开通之后，还需根据7号线的实际客流数据及乘客调研数据，再次对ACC清分算法模型进行优化调整，其中主要进行模型中参数系数/权值设置的准确性分析，对产生偏差的参数系数/权值再次调整修正。由于新线开通，乘客出行的可行路径也将随之发生变化，在保证参数系数/权值设置合理的前提下，重新计算全线网的有效路径集，并修正各路径的客流分配比例。

4 结语

本课题旨在研究当前成都地铁ACC模型中尚未纳入考虑，但由于线网变化对清分计算结果有显著影响的清分因素，从而确定清分算法模型中所需的基础参数数据，如换乘站的换乘走行时间、换乘次数、列车发车间隔等，并根据已有的客流数据进行模型实时分析及算法推导，验证模型中参数系数/权值设置的合理性，以保证清分模型的计算结果最大化地反映实际轨道交通网络的客流分布及收益分配情况。

[1] 徐瑞华，罗钦，高鹏. 基于多路径的城市轨道交通网络客流分布模型及算法研究[J].铁道学报，2009（4）：110-114.

[2] 刘小霞. 城市轨道交通网络突发客流传播影响分析[D].北京交通大学，2011.

[3] 赵路敏，郝庆玲，杜世敏.北京市轨道交通线网客流及票款清分方法[J].都市轨道交通，2009（12）：58-60.

[4] 杜世敏，赵路敏.北京城市轨道交通清分方法及结果应用[J].城市轨道交通研究，2014（2）：106-110.

[5] 卢曙光.深圳市轨道交通清分方法研究[D].西南交通大学，2012.