从积温角度看《黄帝内经》客运太少排序的合理性

2018-03-22柯资能章燕辉

中国中医基础医学杂志 2018年2期

周志，柯资能△，吕游,章燕辉

(1. 中国科学技术大学科技史与科技考古系，合肥 230026； 2. 上海市青浦区人民检察院，上海 201700)

《素问·六元正纪大论》中，每年的客运之初运由中运确定，按照角徵宫商羽五音相生的顺序确定其余四个运，其太少则是由初运的太少分别向前和向后相生而得，“客运太少相生只限于客运初运所在的这一五行周期之内的从角至羽”[1]，下文中称“内经版”。一些学者或以为内经版排序不够直观、合理，改为确定初运之后直接向后太少相生而得，下文中称“创新版”。两个版本的太少排序差异较大，如戊年，内经版：太徵、少宫、太商、少羽终、少角初；而创新版：太徵、少宫、太商、少羽、太角。两个版本哪个更合理，本文根据全国有60年完整气象数据的120多个站点数据作一个验证。

1 资料

笔者从中国气象科学数据共享服务网获取了自1954～2013年间具有完整逐日平均气温记录的129个站点的数据，其中东北24个，西北20个，华北9个，中南23个，华东22个，西南31个。

在这129个站点中，具有完整逐日最高气温记录的有123个站点，其中东北24个，西北20个，华北8个，中南21个，华东20，西南30个；具有完整逐日最低气温记录的有122个，其中东北24个，西北20个，华北8个，中南21个，华东19个，西南30个。

2 方法

2.1 建模与假设

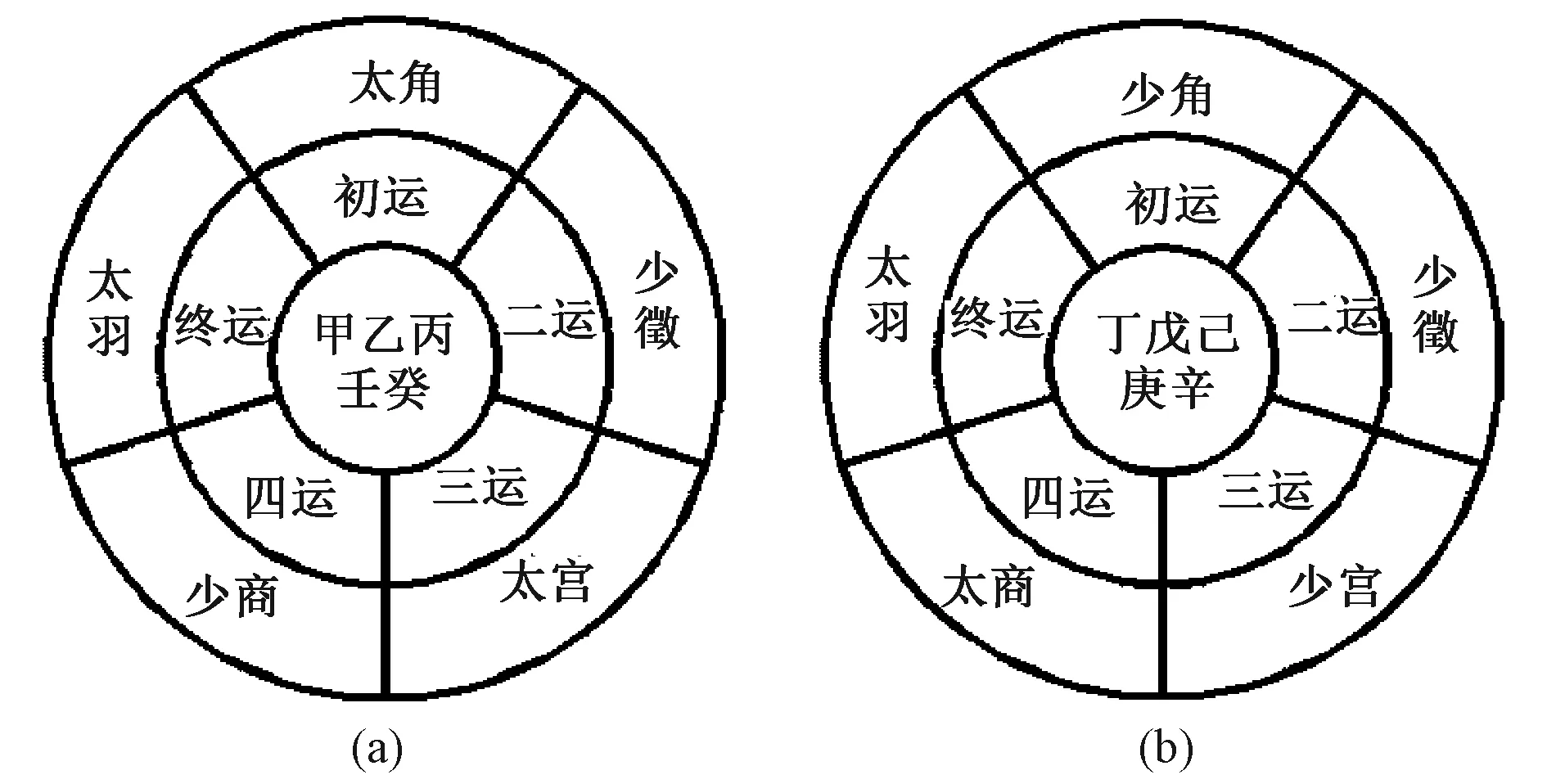
图1 《黄帝内经》客运五步模型图

表1图1显示，根据《素问·六元正纪大论》原文，可以将每年客运五步的规律总结为五音建运和太少相生，具体的五步之运递推见图1，凡逢甲乙丙壬癸五年则见图1(a)，里层的圆环不动，将最外层圆环与当年天干年岁运对应的五音顺时针旋转到初运位置，则该顺序即为当年客运五步；凡逢丁戊己庚辛年则见图1(b)如是操作。客运初运起于大寒日，每运各主73天零5刻(古人将一天分成100刻)，五步合计365天零25刻。天干10年1周期，因此客运五步也是10年1周期。一天干周期内的客运年年不同，但岁运相同年客运五步的五音是相同的，太少正好相反。笔者将其中五音相同但太少正好相反的五步之运称为1个太少对，而1个天干周期有25个太少对。

表1 太少对

温度是最重要的气象因子之一，一个时段的积温反映该地区获得的总热量，可以刻画该时段的寒温特征[]，每一运的积温，即指在这一运之内逐日温度的总和，计算公式为：

其中z表示站台，k表示一年的客运五步，i表示当年的每一天，tz,i表示逐日气温，Tz,k表示每运积温。

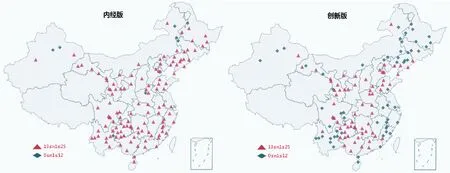
图3 平均气温客运站点分布图

利用上面的数据，求出每个站点每一运的积温，再对所得结果依据相同天干所纪六年求平均，求平均使客气的影响互相抵消，这样得到的是6个天干周期每一运的平均积温，然后对得到的结果依据表1所示比较每一太少对积温的大小。将太时段的积温小于少时段的太少对个数记为n1，太时段的积温大于少时段的太少对个数记为n2，则n1、n2的取值范围为0≤n1,n2≤25，且n1+n2=25。一个n1值惟一确定一个n2值，故分析n1与分析n2值等效，本文选择分析n1值。

图2显示，从数学的角度考虑，一个P=0.5的伯努利事件重复25次是一个服从于x～B(25,0.5)的二项分布。

图2 二项分布的概率函数

为方便讨论，笔者将n1值介于[0,12]之间归为一类，将n1值介于[13,25]之间归为第二类。假如n1的取值是随机的，那么P(0≤n1≤12)=P(13≤n1≤25)=0.5，进一步对多个站点观测到n1值的频数也有P(0≤n1≤12)=P(13≤n1≤25)=0.5，表明客运的排列没有任何实际意义；假如站点n1值的频数显现出偏向性，则表明客运的排列有特殊性。可知在一个天干周期内有50运，则两种方案有20运的太少不同，即有10对太少对的正负值不同，从而n1值不同。笔者将验算“内经版”和“创新版”两种方案下的n1值分布情况，分别对平均气温、最高气温、最低气温3组数据求出每个站点在2种排列方案下的n1值，并依据n1值大小(0≤n1≤12,13≤n1≤25)绘制站点分布图。

3 结果

3.1 站点分布

图3显示，平均气温下“内经版”有121个站点13≤n1≤25，只有8个站点0≤n1≤12，这8个站点分别是郑州、嫩江、白城、奇台、乌鲁木齐、博客图、乌兰浩特、盘县，“创新版”却有接近一半的站点0≤n1≤12。

图4显示，最高气温下“内经版”有113个站点13≤n1≤25，只有10个站点0≤n1≤12，这10个站点分别是兖州、安阳、郑州、开封、齐齐哈尔、白城、临夏、乌兰浩特、海拉尔、思南，“创新版”却有较多的站点0≤n1≤12。

图4 最高气温客运站点分布图

图5显示，最低气温下“内经版”有116个站点13≤n1≤25，只有6个站点0≤n1≤12，这6个站点分别是哈尔滨、章党、丹东、奇台、围场、海拉尔；“创新版”却有接近一半的站点0≤n1≤12。

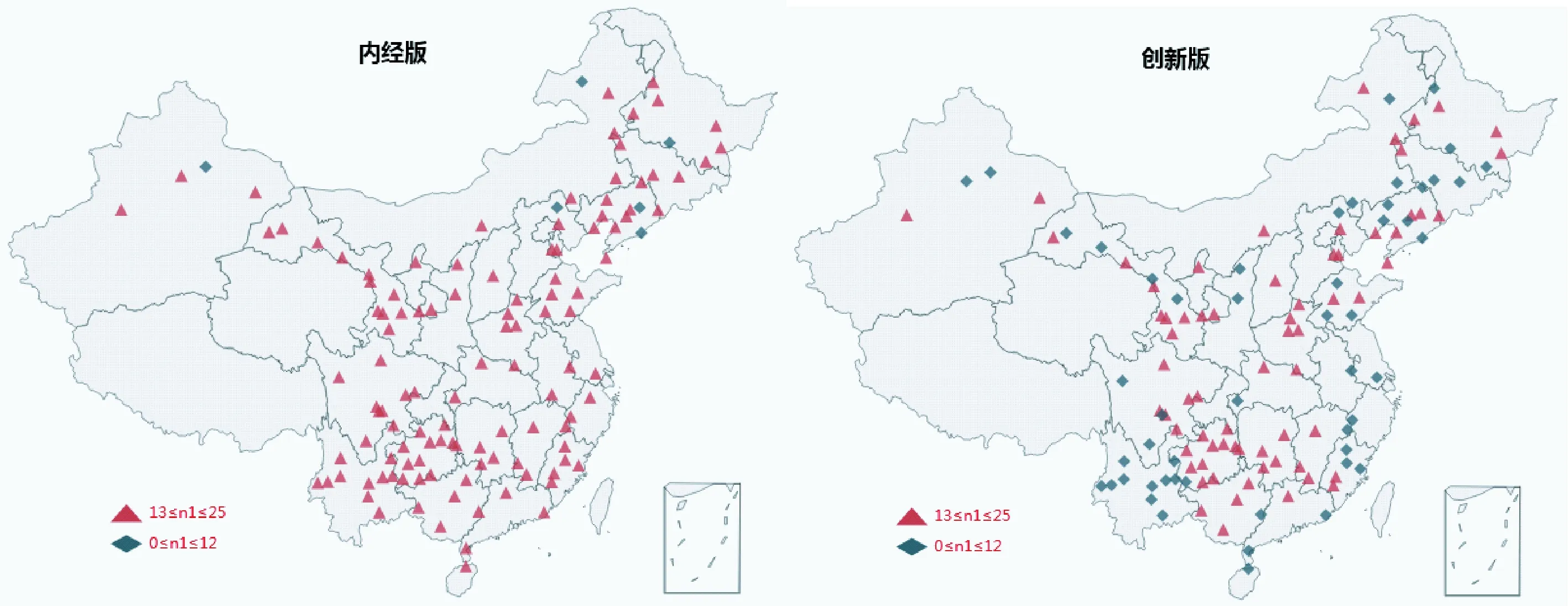
图5 最低气温客运站点分布图

3.2 比例分布

图6～8显示，两种方案在3个气温维度上有很大差异，“内经版”中平均气温维度下0≤n1≤12的站点只占6%，而13≤n1≤25的站点占94%；最高气温维度下0≤n1≤12的站点只占8%，而13≤n1≤25的站点占92%；最低气温维度下0≤n1≤12的站点只占5%，而13≤n1≤25的站点占95%。“创新版”中平均气温维度下0≤n1≤12的站点占47.2%，而13≤n1≤25的站点占52.7%；最高气温维度下0≤n1≤12的站点占28.5%，而13≤n1≤25的站点占71.5%；最低气温维度下0≤n1≤12的站点占43.4%，而13≤n1≤25的站点占56.6%。

图6 平均气温下两种方案比例分布

图7 最高气温下两种方案比例分布

图8 最低气温下两种方案比例分布

表2 “内经版”的站点分布比例

3.3 假设检验

表3显示，笔者对“内经版”的站点分布即n1值的频数作二项式检验，设每个站点的n1值落在[0,12]的概率为0.5，即令原假设H0:P(0≤n1≤12)=0.5，备择假设H0:P(0≤n1≤12)≠0.5，利用SPSS得到每个气温尺度下的显著性值，P均远远小于α=0.001，故拒绝原假设，认为n1落在[13,25]的概率远大于0.5，结果有统计学意义。

表2 “创新版”的站点分布比例

表3 《内经》版客运排列的二项式检验

表4 创新版客运排列的二项式检验

表4显示，依据如上方法，笔者再对“创新版”的站点分布即n1值的频数作二项式检验。

“创新版”在平均气温和最低气温维度下的显著性值P值都大于0.05，故接受原假设。可见，这种情况下n1值的频数大致满足P(0≤n1≤12)=P(13≤n1≤25)=0.5，即n1的取值是随机的。出现n1的取值区间落在[13,25]偏高的原因，是在“创新版”的排列方式下，有部分顺序与“内经版”的排列方式是一致的。这种随机性则反证了这种排列方法的错误。

4 讨论

客运五步循环相生，每运短暂地主司一步的气候变化，相较于主运，客运对异常气候可能有更明显的反映。客运随中运变化而年年不同，而岁运变化反映到客运有两个明显的特征，其一是每一步的本气变化，其二则是该本气太过不及的变化。太少对的本气相同，太过不及正好相反，一个太少对2个运的积温变化正好反映了太过和不及的差别。由《内经》中的客运排列方式来看，一个周期25个太少对中太的积温小于少的积温的对数总是占多数，即n1值落在区间[13,25]的概率远大于0.5，证明客运的这种排列有其特异性。

值得注意的是，太过和不及并不像平时理解的那样，太过积温偏高，太时段的积温小于少时段的积温反而占绝大多数。细品其因，太过主发散，热量积累不足；不及主收敛，积累热量反而多，故而整体上太少对在客运是太的时段的积温比客运是少的时段要低。