面向星表探测的航天服关节系统概念设计

王振伟，胥任杰，刘双印，徐利梅，谢晓梅，范守文

（电子科技大学航空航天学院，成都611731）

1 引言

航天服是航天员进行星表与太空作业的重要生命支撑保障系统。与太空作业不同，星表作业要求航天服上下肢关节系统都具备较好的运动性和灵活性，以便完成星表行走、探测、维修、搬运等任务。在内压作用下，航天服多层织物刚性将明显增强，材质物理属性和力学特性都将发生变化，导致航天服关节系统产生较大的运动阻力，增大星表作业难度。以美国STS航天服为例，在29.67 kPa内压情况下，关节运动范围平均减少约15%［1］。为了提高航天服关节活动性，航天服关节通常采用织物褶皱［1⁃2］、活动框架［3⁃4］和旋转轴承结构［5⁃6］等，如美国“水星”航天服、“双子星”航天服、“MARK III”、“Z⁃1”、“Z⁃2”、俄罗斯“海鹰”航天服、中国“飞天”航天服等。围绕航天服关节系统，目前许多研究工作主要集中在关节设计［6］、阻力／阻力矩分析［7］、动态性能计算［8］、实验测试［9］、 织 物材 料属性［6，9］、 人机交 互性能［10］等方面。随着太空探测任务的不断深入，对其它天体的星表探测存在较大的任务需求，例如月球、火星、土星等星表探测，这对航天服下肢关节系统研究提出了更高的要求。与膝关节和踝关节相比，作为下肢活动的主要部件，髋关节研究相对滞后，有关的设计方法与性能分析引起了学者的广泛关注。

本文提出一种硬式冗余自由度航天服旋转关节系统概念，给出关节系统概念设计依据和自由度配置方案，分析上下肢关节系统的运动范围和包络，建立航天服关节系统的概念设计模型，并完成运动仿真分析，以验证方案可行性。

2 航天服整体、上肢及视野的概念设计

本文提出的航天服关节系统的概念设计模型如图1所示。提出的航天服概念设计模型主要包括：头盔、照明摄像系统、生命支撑保障系统、手套、肩关节、肘关节、上躯干、下躯干、腕关节、肘关节、腰关节、髋关节、膝关节、大腿、小腿、踝关节、靴子等组件，具有24（2×12）个自由度。本文将重点研究航天服关节设计。

为了提高进出舱效率，采用“后背进入式”的舱门设计方案，舱门由腰关节上部开始，一直延展到头盔顶部。相比“腰背进入式”的舱门设计方案，“后背进入式”设计方案具有结构紧凑、进出方便、节省空间、平衡性好等特点，是目前较为认可的设计方案。

图1 航天服整体概念设计模型Fig．1 Conceptual design model of space suit

通常，男用／女用航天服是存在差异的，设计参数具有不同的参考要求，如肩宽、腰围、臀围等，因此，它们的设计参数选取需区别对待。目前，NASA已建立了面向星表作业的人机工程设计参考规范和文档，形成了完整的人机功效测试分析方法与流程。考虑到航天员个体的差异，NASA人机工程设计规范很难适用于我国航天服的设计需求，因此，本文采用我国颁布的有关人机工程标准或规范作为设计依据。我国人机工程标准或规范规定了较多的参考指标和测量项目，因此需对这些指标和测量项目进行设计需求的筛选，提取出紧密相关的设计参数项目。这里，选取了与躯干、上肢和下肢关节设计有关的8个主要数据，并以＞95%样本区间作为参数选取依据，力求最大限度地涵盖设计数据项。

具体而言，选取了我国《GB／T 10 000－1988人体主要尺寸和立姿人体尺寸数据》［11］作为航天服关节系统概念设计的参照标准，选取了我国《GB／T5703－1999人体测量基础项目》［11］作为关节系统设计参数的换算分析依据。根据该标准的推荐统计数据，在26～35岁区间，我国成年男性身高主要集中1755～1776 mm区间，女性身高主要集中在1642～1661 mm区间。考虑到该标准颁布时间较早，目前人体身高数据可能要比推荐数据大一些，这里选取推荐区间的上限值作为航天服关节系统的设计依据。拟定的男航天员参考设计身高为1776 mm，女航天员参考设计身高为1661 mm。然后，运用线性插值法确定其它的主要设计参数，具体计算结果如表1所示。考虑到男用／女用航天服设计理论与方法的相似性，下文将主要以男用航天服为对象，论述航天服关节系统的概念设计与建模。

表1 航天服的主要设计参数Table 1 The main design parameters of space suit ／mm

依据表1中的相关设计参数，拟定了航天服上肢关节系统主要包括肩关节、肘关节和腕关节。其中，肩关节设计为3个自由度，肘和腕关节各设计为1个自由度。设计参数指标为：外摆／内摆活动范围为＋180°～－30°、上摆／下摆活动范围为＋180°～ －45°、前摆／后摆活动范围为 ＋140°～－40°、下臂与上臂间的弯曲／伸展范围为＋145°～－0°。通过肩关节、腕关节与肘关节的配合操作，上肢关节系统完成双手触头盔、双手提物、双手胸前交叉、双手举物、单手触肩、直臂等动作，具体情况如图2所示。由于航天服肩关节设计角度尺寸的限制，在单手触肩动作中，手臂活动极限位置为肩部锁骨处，未达到肩关节的最大位置。因此，躯干与头盔的设计需以上述手臂的极限位置作为强尺寸约束，并将照明装置和摄像装备布置在上躯干与头盔连接处的强尺寸范围内。这里，照明与摄像装备均采用外置人工操控的设计方案，航天员根据实际情况进行操作。相比内置式设计方案，外置式方案的照明效果、成像质量和控制方式更为灵活、高效。

为了获得较宽的观察视野，采用了大直径球头盔的设计方案。此外，大直径球头盔的设计方案，与NASA Z系列的椭球头盔相比，具有良好加工性、力学性能和实用性，便于保护罩和遮阳罩的设计、制造和安装。头盔设计选取了我国《DL／T 575.2－1999直接视野范围》［11］中的推荐指标作为设计依据。具体而言，选取标准中的最大水平观察视野要求作为头盔的横向极限定位尺寸和生命保障支持系统的极限宽度，将双眼极限范围设计为 ＋110°～－110°，将单眼极限范围设计为＋140°～－140°，上述参数范围涵盖了最佳水平观察视野要求（＋55°～－55°）；选取标准中的最大垂直观察视野要求作为头盔的纵向极限定位尺寸和生命保障支持系统的极限高度，将头部垂直极限范围设计为＋30°～－40°，其对应观察范围为＋100°～－90°，上述设计参数涵盖了最佳垂直观察视野要求（＋50°～－50°），观察视野范围分布如图3所示。

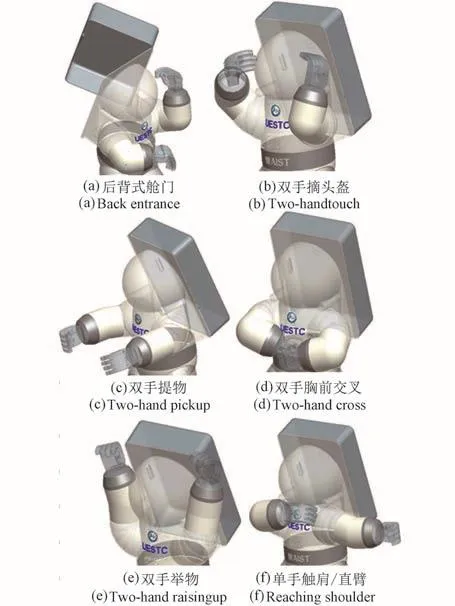
图2 航天服上肢关节系统的动作分类Fig．2 Mobility examples of upper limb joints

3 航天服下肢髋关节概念设计

3.1 髋关节配置方案

髋关节是影响航天服下肢活动的重要部件，它的活动范围和灵活性将直接影响未来星表作业的效率和安全性。通常，髋关节和肩关节可采用相同设计方案，如织物褶皱软关节、硬质轴承关节或半硬关节结构。但是，应该根据它们的功能和作用，选取相应的概念设计方案。肩关节和髋关节的主要差别：1）髋关节主要功能是承载躯干重量和提供下肢活动能力；除了搬运重物，肩关节不承载躯干重量，外界载荷较小且作用时间短，重点是灵活性。2）髋关节通常需具备较好的动态性能，以保证星表作业的安全性和高效性，最大限度地降低星表作业的阻力或阻力矩，节约航天员体能；肩关节的平衡性和安全性需求不很明显，较小的受力承载使得运动阻力和阻力矩较小，有时可以忽略，主要关注上肢活动的精确性。3）左右肩关节的间距相对较远，互相关涉概率较小，肩关节设计空间较大，设计约束较松弛；髋关节的左右腿较为接近，互相关涉问题较为明显，因此，髋关节设计空间较为狭小，运动空间的约束限制较为严格。

图3 观察视野Fig．3 View range of space suit

就髋关节设计而言，需考虑星表环境、任务需求、平衡性能等因素。对于未来星表探索任务，航天服下肢关节系统可能面临比地面更大或等量的重量载荷。例如土星引力加速度系数约为地球引力加速度系数的2.53倍、木星引力加速度系数约为地球引力加速度系数的1.07倍。因此，若采用软式髋关节的设计方案，由于它的承载能力有限，使得航天员将承担大部分航天服自重。相反，硬式髋关节则可利用自身结构强度，承担航天服自重，减轻航天员载荷负重，甚至可以起到自主支撑的作用。以NASA Z系列为例，其重量范围为64.9 kg ～71.2 kg［12］，未来火星探测任务（其引力加速度系数是地球的0.38倍）中髋关节将承担24.6 kg～26.9 kg的航天服重量。可见，航天服重量载荷是较为明显的，尤其是高引力系数的星表探测。

综上所述，采用硬式髋关节的设计方案是合理的，能较好地满足低重力星表探测的任务需求，最终拟定的航天服关节系统的配置方案如表2所示。此外，硬式关节具有较好的动态特性，能在关节活动过程中保持容积不变，避免服内压力波动所引起的阻力与阻力矩，提高关节的活动性和灵活性。由于软式关节设计开发研究较早，技术较成熟，已得到了实际应用，在此不赘述。下面，主要论述硬式髋关节的设计原理与参数计算。

表2 航天服关节系统配置Table 2 Design scheme of joint system

3.2 髋关节方案设计

针对下肢髋关节，提出了“硬式冗余自由度旋转关节”概念设计方案，以期获得较为宽泛的活动性和较强的灵活性，如图4所示。主要包括旋架J0、旋架J1、旋架J2、旋架 J3、若干旋转轴承等部件。在各旋架的上下连接面，分别设计轴承连接孔和轴承安装孔，用来实现旋架之间的装配连接。4个旋架之间通过旋转轴承实现连接。髋关节的不同运动状态被分解为旋架间的相对旋转运动，即实现了髋关节弯曲运动到旋架相对转动的运动转换。4个旋架采用了“半球冠平面斜截”的设计方法，即在半球冠上，做通过球冠某一直径的斜平面，选取斜平面与直径面之间部分作为旋架模型。4个旋架具有相同的装配轴，它们都位于初始旋架J0的直径面切线上。

图4 硬式髋关节概念设计模型Fig．4 Conceptual design model of hard hip join

由图4可见，旋架的设计构型比较简单，主要设计参数为：初始旋架J0的半径R0和斜平面倾角α。根据表1的设计参数，这里令所有旋架具有相同的斜角α＝20°（根据设计需要，也可采用不同斜角）。令初始旋架J0为半径R0＝110 mm。由几何关系可知，所有旋架的斜角之和就是髋关节运动的极限范围，因此，髋关节运动范围为＋80°～－80°。在此基础上，按髋关节的弯曲／伸展设计要求，确定腰关节连接安装面的倾斜角度。令髋关节的弯曲／伸展的设计要求为140°／20°，则下躯干腰关节连接面的外倾斜角度为20°。

下面，将讨论各旋架的轴承连接孔设计尺寸的计算公式。根据髋关节的概念设计模型，在髋关节各旋架轴承安装孔中心处，分别建立相应的局部坐标系（xi， yi， zi），i＝ 1，2，3，4。 在旋架 J0的轴承安装孔中心处，建立全局坐标系（x，y，z），坐标系统分布如图5所示。

由于髋关节为球冠对称结构，设旋架轴承安装孔平面为xy平面，各旋架轴承安装孔中心设为相应坐标系的原点。初始状态下，所有坐标的yz坐标面处于同一个平面，即各个坐标系的x轴相互平行。从设计构型来看，这是髋关节的极限运动状态。另外，分别连接旋架轴承连接孔中心与轴承安装孔中心，形成了各旋架中心矢量Hi，i＝1，2，3，4。设各旋架中心矢径Hi与相应的局部坐标系（xi， yi， zi）的 z轴夹角分别为 θi。 连接全局坐标系原点O和旋架J4的轴承连接孔中心C，形成了方位矢量S。令各旋架球冠半径Ri，i＝1，2，3，4。由旋架上下连接面的几何关系，可得到各旋架轴承连接孔的设计尺寸为：R1＝R0cosθ1，R2＝R1cosθ2，R3＝ R2cosθ3，R4＝ R3cosθ4。

观察上述各式，通过算式迭代，可得旋架轴承连接孔尺寸的计算公式如式（1）所示：

依据髋关节数学模型（图5），可对髋关节自由度进行分析。从运动原理来讲，髋关节各旋架的运动可看作为刚体定轴转动，且各旋架轴承连接孔中心矢量长度不变，只是旋转姿态各不同。因此，髋关节运动状态可采用空间多刚体系统理论进行分析计算。为了获得髋关节的运动规律，采用欧拉角描述各旋架的运动姿态。设欧拉角分别为进动角φ、章动角θ和自旋角ω。这样，各旋架姿态可表达为（φi， θi， ωi），i＝1，2，3，4。 由旋架J0与基座的连接关系，旋架J0上局部坐标（x1， y1， z1）与全局坐标系（x， y， z）相重合，其 z坐标轴为旋架固定旋转轴。因此，旋架J0的姿态为（0，0，w1），w1为独立自由变量。 旋架 J1 上的局部坐标系（x2， y2， z2）相对全局坐标系（x， y，z）进行定轴转动，初始状态下它们的x轴是相互平行的，旋架J2围绕局部坐标系的z2轴定轴旋转。 因此，旋架 J1 的姿态为（0， θ1， w1），w2为独立自由变量。同理，可分别得到旋架J2和J3的姿态（0， θ1＋ θ2， w3）和（0， θ1＋ θ2＋ θ3， w4），其中w3和w4为独立自由变量。

综上，硬式旋转髋关节设计方案具备4个独立自由变量 w1、w2、w3和 w4，或者说存在一个冗余自由度。因此，空间任意方位向量S可表达为式（2）：

其中，Ti和分别为对应旋架相对全局坐标系的旋转矩阵和中心矢量Hi在相应局部坐标系中的相对矢量。由空间坐标变换和矢量关系，可以得到Ti和表达式如公式（3）：

将公式（3）带入公式（2），便可得到方位向量S计算表达式。然后，采用数值计算方法，获得髋关节任意空间方位向量所对应各旋架的姿态解。旋架姿态通常采用数值计算方法，从而得到姿态的数值解。限于篇幅原因，具体数值计算过程不再讨论，详细数值计算方法和过程可参见多刚体系统文献［13］和［14］。

在上述内容基础上，基于Pro／E三维建模和仿真系统进行了航天服下肢关节系统的仿真验证。所提出的航天服下肢系统可实现步态行走、屈膝下蹲、双手拾物、外展、内收、内弯等活动，具体的仿真验证结果如图6所示。可见，所设计概念模型满足下肢运动的指标要求。需要指出，在双手拾物动作中，由于设定腰关节活动范围为＋5°～－5°，因此上肢运动范围略短。针对不同作业距离要求，需将腰关节活动范围适当增大。理论上讲，由于髋关节存在4个自由度，就任意空间方位矢量S而言，4个旋架可能存在3组不同的姿态解，即（wi，wj，wk），i≠j≠k，i，j，k ＝ 1，2，3，4。这是由冗余自由度所引起的不定解现象。冗余自由度设计方法不但可满足髋关节3个旋转运动需求，而且极大地改善了髋关节的活动性和灵活性。但是，冗余自由度的存在可能导致机构运动的不确定性，也可能导致旋架与外界物体的意外接触。因此，应尽量将各旋架的运动包络限制在合理范围内。由公式（1）可知，所提出的髋关节旋架轴承连接孔的最大直径是依次递减，最大包络面直径为2R0，具有明确的极限运动范围。因此，髋关节运动是完全可控的。

图6 航天服下肢关节系统的动作示例Fig．6 Mobility examples of lower limb joint

综上，所提出的硬式冗余自由度旋转髋关节设计方案是合理、可行的，满足星表作业环境下的航天服下肢活动需求。

4 结论

1）针对未来星表作业，提出了硬式冗余自由度旋转关节的航天服关节系统概念设计模型。它由肩、肘、腕、髋、腰、膝、踝等关节组成，共具有24（2×12）个自由度，可完成头盔放置／摘取、胸前工作台器具操作、双手抬举物体、单手触肩、直臂取物等上肢活动，满足未来星表作业上肢运动需求。

2）以航天服下肢髋关节为对象，提出了“半球冠斜平面截取”的硬式关节设计方法，给出了髋关节重要尺寸的设计与计算方法，完成了髋关节的冗余自由度分析。仿真表明，所提出的髋关节可实现步态行走、屈膝下蹲、双手取物、内收、外展、内弯等下肢活动。

3）未来工作主要集中在航天服关节系统的动态特性分析，以及生命支撑保障系统的重心平衡设计，为航天服关节系统的优化设计提供技术支撑。

（

）

［1］ Schmidt P B.An Investigation of Space Suit Mobility with Ap⁃plications to EVA Operations［D］.Massachusetts Institute of Technology，1996.

［2］ Vykukal H C.Shoulder and hip joint for hard space suits：U.S.， 4594734［P］.1986.

［3］ Vykukal H C.Shoulder and hip joint for hard space suits and the like： U.S.， 4598428［P］.1986.

［ 4 ］ Vykukal H C.Hard Space Suit： U.S.， 3405406［P］.1966.

［5］ Vykukal H C.Elbow and knee joint for hard space suits：U.S.， 4598427［P］.1986.

［6］ Vykukal H C.Spacesuit mobility joints： U.S.， 4091464［P］.1978.

［7］ Anderson I P，Stoklitsky A Y，Barer A S，et al.Essential as⁃pects of space suit operating pressure trade⁃off［C］ ／／Pro⁃ceedings of the international conference on Environmental sys⁃tems， U.S.， 1994：125⁃130.

［8］ Webb G，Kurdila A，Lagoudas D.Adaptive hysteresis model for model reference control with actuator hysteresis［J］.Jour⁃nal of Guidance， Control， and Dynamics， 2000， 23（3）：459⁃465.

［9］ Heather N.Bradshaw1，Dr.David L.Akin.A range of mo⁃tion study and human⁃suit correlation analysis supporting the morphing spacesuit concept［C］ ／／41st International Confer⁃ence on Environmental Systems， U.S.： 2011：17⁃21.

［10］ Möller P， Loewens R， Abramov I P， et al.EVA suit 2000：A joint European／Russian space suit design［J］.Acta astro⁃nautica， 1995， 36（1）： 53⁃63.

［11］ 秦大同，谢里阳.机械设计手册（第6卷）［M］.北京：化学工业出版社，2010.Qin Datong， Xie Liyang.Machine design handbook （Vol.6）［M］.Beijing： Chemical Industry Press， 2010.（in Chinese）

［12］ Pierre J Bertrand， Allison Anderson， Alexandra Hilbert， et al.Feasibility of spacesuit kinematics and human⁃suit interac⁃tions［ C］ ／／44th International Conference on Environmental Systems， Holland： ICES， 2014： 13⁃17.

［13］ 刘延柱，潘振宽，戈新生.多体系统动力学［M］.北京：高等教育出版社，2014.Liu Yanzhu， Pan Zhenkuan， Ge Xinsheng.Multi⁃body Dy⁃namic［M］.Beijing： High education Press， 2014.（in Chi⁃nese）

［14］ 洪嘉振.计算多体系统动力学［M］.北京：高等教育出版社，1999.Hong Jiazhen.Computation Multi⁃body Dynamic［ M］.Bei⁃jing： High Education Press， 1999.（in Chinese）