降低数字集成电路测试功耗的向量排序方法

张建文

（华润赛美科微电子(深圳)有限公司，广东深圳，518000）

0 引言

随着微米技术的深度发展，逐渐提升了集成电路的复杂程度，降低占用面积，加强运行效率，在实际测试期间需要全面注重功耗这一技术参数。在设计集成电路的各个环节当中能够全面展现出多样化的低功耗技术。在集成电路生产当中最重要的就是测试环节，功耗能够在测试模式影响下会加大其消耗程度，在实际测试期间，被测电路如果出现较大的功耗，将会损坏芯片，并且进一步降低测试的可靠性，逐渐减少使用时间。在设计测试环节当中如何更好地降低功耗已经成为现阶段大多数研究学者关注的热点问题。

1 测试功耗向量排序法概述

功耗测试能够分为静态和动态两种方式，动态功耗会受到测试向量排序的影响，该种消耗主要是由于电路内部各个门逐渐转化状态时出现的现象。在对向量进行测试时首先需要确定，测试向量的正常排序在较大程度上会对动态功耗产生影响。如果没有对测试向量的排序进行优化，将会导致其出现较大的测试功耗。现阶段在向量排序方式主要包括海明距离测试法以及在测试向量时统计电路内部每一份节点的状态，之后按照以上状态对测试向量进行排序，这样能够减少电路内部状态的翻转次数。该种测试方式主要应用在较小规模的电路上，然而由于现阶段逐渐增大电路规模，出现了非常强大的节点数量，因此在实际测量排序时需要对n个向量进行排序，此时就需要使用逻辑模拟方式进行，并且在对两向量之间的距离所花费的时间进行计算时，将会提升计算时间，降低工作效率。

2 功耗模型

现阶段，CMOS电路在运行期间产生的功耗大多数都是由于电路内部出现的逻辑门状态产生变化，使其出现充放电消耗功率，如果改变测试向量，将会导致电路消耗的功率改变为以下：

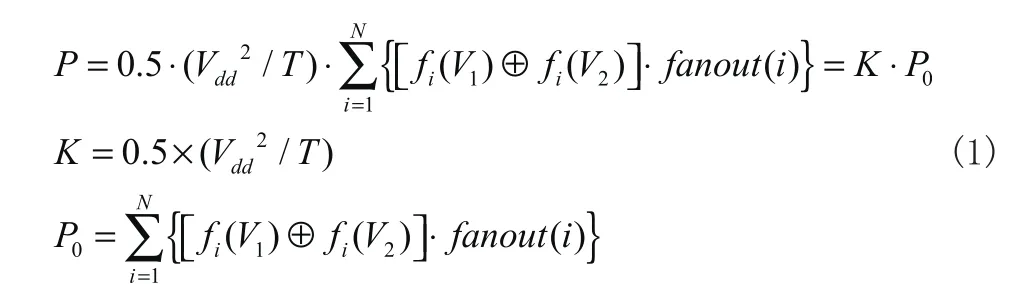
在以上式子当中，ddV 表示电路的供电电压，T表示电路的时钟周期，N表示电路中门的数量，i表示某一个门。

3 影响度系数的确定

3.1 电路状态变化与结构之间的关联性

下图为该电路的结构图，输入端有5个，与非门有6个，各个门的状态与输入端（c）有关，这就表明输入端（c）如果产生变化，将会导致6个与非门状态都产生变化。但是，a与e只和其中2个门有关联，因此如果这两个出现变化将会导致2个门状态发生改变。由以上可以看出，功耗与电路结构之间存在较大的关联性。

3.2 电路状态与测试集之间的关联性

在对这两个指标进行研究时，需要使用到1号与非门进行分析，如果测试集已经明确，并且测试向量当中c值为0，那么在此情况下，如果a出现变化情况将不会对g的状态产生影响。如果c值为1，如果a出现变化情况将会对g的状态产生影响。由以上分析可以看出，测试集当中的输入取值与门的状态之间存在较大的关联性。以上存在的影响关系可以称为输入与电路活性之间的关系，在表示各输入端变化情况时采用影响度系数，这样能够全面展现出电路活动性的影响程度，进一步按照影响度系数排列测试向量。

图1 电路结构

3.3 明确输入端与电路状态变化的影响度系数

由于单个背侧点苦当中存n个原始输入，并且在每一门当中存在m个门，g主要是表示电路级数，T为故障测试集，测试集当中的测试向量为Vi。定义：电路第i个原始输入对门变化状态的影响度系数为：

在以上式子当中，xy主要是表示门的直接输入，Wix表示i对x的影响度系数，p( y = k ey)表示在实际测试期间y取key的概率。对与门来说，如果key的值为0时，针对缓冲门和非门来说由于只存在一个直接输入，因此需要将输入假设为x，那么此时Wiy= Wix。在电路当中，所输入门主要是由2个输入门组成，需要对其影响度系数进行分别计算。原始输入度g值为1的门影响度系数与输入取key中的概率相同。

定义：当电路第i个原始输入对电路变化状态的影响度系数为

按照下图所示，当中测试集为 {（10100），（01000），（01110），（01010）......}时，b对电路状态变化影响度系数由b对门2.6.7.9.10状态的影响度系数；b对2门的影响度系数为1，对6门的影响度系数为 Wb2× p( h =1)。对7门的影响度系数为Wb2× p( j =0)，对9门的影响度系数为Wb2× p( k=0)……，在以上影响度系数当中，h，j，i，k都是该门的key值的概率，这样就能够对各个原始输入对电路状态变化的影响度系数进行计算。

图2 被测电路

4 优化测试集排序

上文主要对所有原始输入都给予了对应的影响度系数，该值主要包括原始输入比阿奴啊影响电路状态变化的程度。可以通过该值对海明距离进行修正，这样就能够想成加权海明距离，之后需要借助于等效的排序返回事故会优化测试集。按照以下步骤进行。

该环节的研究主要是将图2的被测电路作为研究对象，将测试量分别记作 V1, V2, V3, V4, V5, V6，之后需要将各个原始测试向量对应原始输入。在两向量之间的海明距离为不同取值范围内的原始输入数量。例如在V1和V2之间的海明距离值为3，在加权海明距离当中需要按照位求异或处理两向量，之后需要对各个原始的影响范围按照位乘进行处理，之后再进行求和处理。

在排序测试集时可以通过贪心算法进行，该测试方式与海明距离排序方法比较类似，下图为加权海明距离测试向量排序方法的流程，。在选择第一个测试向量时主要是通过随机选取向量的方式。，之后在选择下一个向量时需要按照海明距离最小的向量进行选择，需要将回溯算法加入到算法当中，如果两向量的加权海明距离远远超过最大距离的二分之一，那么在选取首个测试向量时需要选择第i个向量，之后再进行排序处理。在完成排序之后，就会明显缩小测试集的加权海明距离，这样能够避免电路在测试期间产生较大的变化，进一步降低测试功耗。

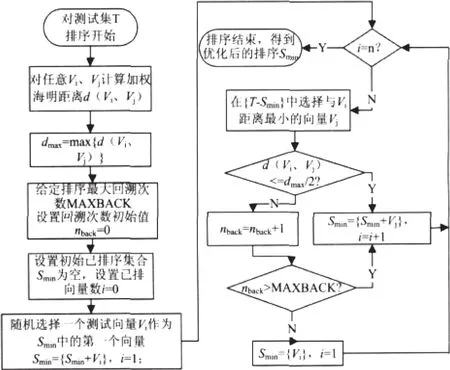
图3 加权海明距离的测试向量排序算法

在下图当中，被测电路为s1488，内部加权跳变数为：

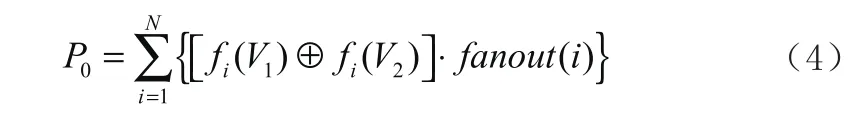
从以上分析可以看出，如果P0越小，在实际测试期间就会降低消耗功率，从上图能够看出，随着不断缩小的加权海明距离，也会相应缩小被测电路内部加权跳变数，因此也会相应降低消耗功率。在对测试集进行优化时能够通过加权海明距离实现，这样能够在较大程度上降低测试期间产生的功耗情况。

5 实验结果与分析

此次研究主要是使用ISCAS85的部分电路，在测试设计阶段主要是通过全扫描方式，测试集主要是应用MINTEST，提过Mat lab软件对程序进行优化，在实际优化期间使用贪心算法，在评价各电路活动性时主要是将被测电路内部加权跳变系数作为标准。

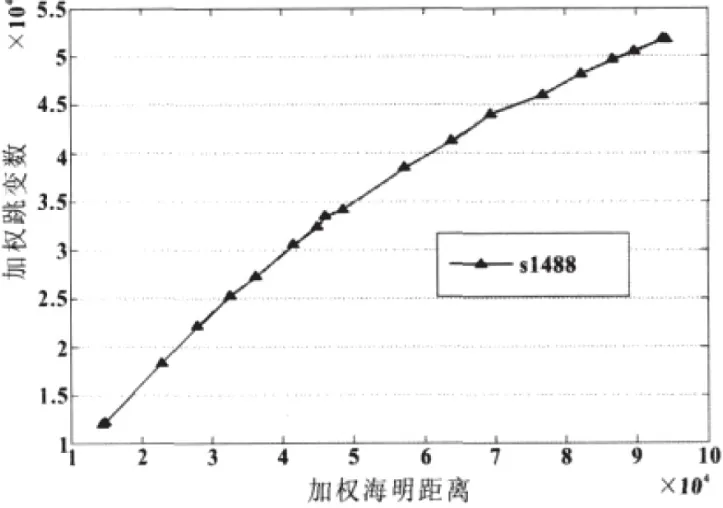
图4 电路加权变数与加权海明距离之间的关联性

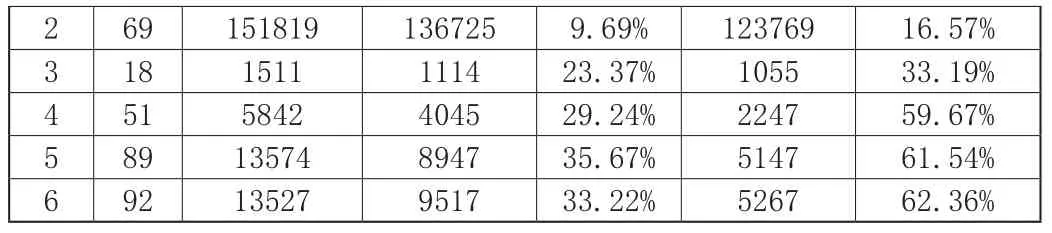
下表主要是对比分析各个电路的海明距离测试期间电路活动性，此研究方法，电路原排序以及测试集当中存在的向量数量，还包括原测试集在测试期间被测电路出现的加权跳变数。由以上可见，相比于海明距离法，此次研究所应用的方法，在优化电路活动性方面存在较大的优势，在测试时间方面，两种测试方式所需时间的差异性较小。

表1 对比分析测试排序方法的结果

2 69 151819 136725 9.69% 123769 16.57%3 18 1511 1114 23.37% 1055 33.19%4 51 5842 4045 29.24% 2247 59.67%5 89 13574 8947 35.67% 5147 61.54%6 92 13527 9517 33.22% 5267 62.36%

6 结论

在此时数字集成电路时，需要全面深入研究其产生功耗的原因以及来源，并且在原有的设计基础之上进行优化和改善，提出新的向量排序测试方法。该种测试方式能够对电路结构以及测试集信息进行全面分析，阐述电路内部状态变化和输入端之间的关联性，之后按照该种关联性重新对测试集进行排序，这样就能够实现对测试集的优化。在完成排序之后需要减少在实际测试期间电路状态翻转次数，这样能够最大限度降低测试前电路的功率消耗问题。该种测试方式最大优势在于不会对测试集产生改变，不会影响故障覆盖率。

[1]张帆.一种低功耗数字集成电路自检电路设计方法[J].科技经济导刊 ,2017,18(16)：76+72.

[2]严梓扬,苏成悦,张宏鑫.Vhd l在数字集成电路设计中的应用分析[J].自动化与仪器仪表,2017,19(05)：131-133.

[3]李娜.数字集成电路低功耗优化设计解析[J].通讯世界 ,2016,22(15)：56.