振动对管内流体对流传热影响实验研究

吕 平， 刘 文 杰， 张 博， 杨 竹 强

( 大连理工大学 能源与动力学院， 辽宁 大连 116024 )

0 引 言

振动是机械设备运转中不可避免的现象．从振动产生的原因来看，主要有以下两类:一类是由设备的动力装置如电机、压缩机的运转而引起的；另一类是由流体绕流固体时，比如换热器中的管束流体诱导振动引起的．研究振动作用对实际的生产和生活有广泛的意义，而对于设备自身振动过程，人们以往倾向于抑制振动，消除其对设备安全性的危害，对于振动对传热影响的研究较少．然而忽视振动对这类传热过程的影响将会导致较为严重的安全性和经济性问题．

振动对传热影响的研究可以追溯到20世纪60～70年代，对于自然对流，振动条件下换热系数可以增加2～5倍[1-2]；其中Penney等[2]还发现相对水平的加热丝而言振动对垂直方向的影响更大，但其没有给出更详细的解释，现在可知这与边界层的发展和变化有关．圆管作为换热器的基础部件，有学者实验研究了振动圆管在静止或流动的流体中自然对流和强制对流换热，结果显示换热系数最大提升了4倍[3-7]．Scanlan[8]研究了垂直于换热平板的振动对传热的影响，显示换热系数增强3倍，换热与振幅成正比，最佳换热频率为100 Hz．随着计算机科学技术的发展，现阶段又出现了大量的仿真计算，为研究振动与流动和传热之间耦合作用机理提供了帮助．Shi等[9]研究了自由柔性振动片在流体通道内的换热情况，使用CFD和CSD求解器相耦合的方法，利用ALE处理变形网格，得出流道传热强化90.1%．吴艳阳等[10]采用Fluent动网格技术研究了振动圆管内流体流动与换热特性，并采用场协同的方法进行分析，发现振幅1～5 mm，频率2～10 Hz，振动能强化传热，且传热效果随振动频率和振幅的增加而增强，传热系数最多提高71%，并指出当相位为90°时场协同性最好，传热效果最好．

国内外学者虽对此进行了大量的研究，但很少有人使用振动加速度进行共振频率的测量，对于管内层流流动在高频低振幅条件下的对流换热也鲜有人研究，而在实际过程中，管内流动换热经常出现在高频振动中，因此有必要进行实验，开展相关的研究．

1 实 验

1.1 实验系统

实验系统主要包括实验测试部分、振动部分、电加热部分、水循环系统部分、温度和振动信号数据采集部分．实验系统示意图如图1所示．

(1)实验测试部分

实验采用TP2型铜管，测试段长度为1 m，外径为9.52 mm，内径为8.72 mm，测试段如图1圆内所示．外层为发泡树脂泡沫保温材料，内部包含高温布，内层为35 Ω/m的电加热系统线圈，均匀紧密缠绕在铜管上，加热温度最高50 ℃，出口和进口处需要钻一个开口放入点式K型热电偶，使用专用的导热性能好的热电偶胶Satlon D-3和催化剂606快速凝固封口．

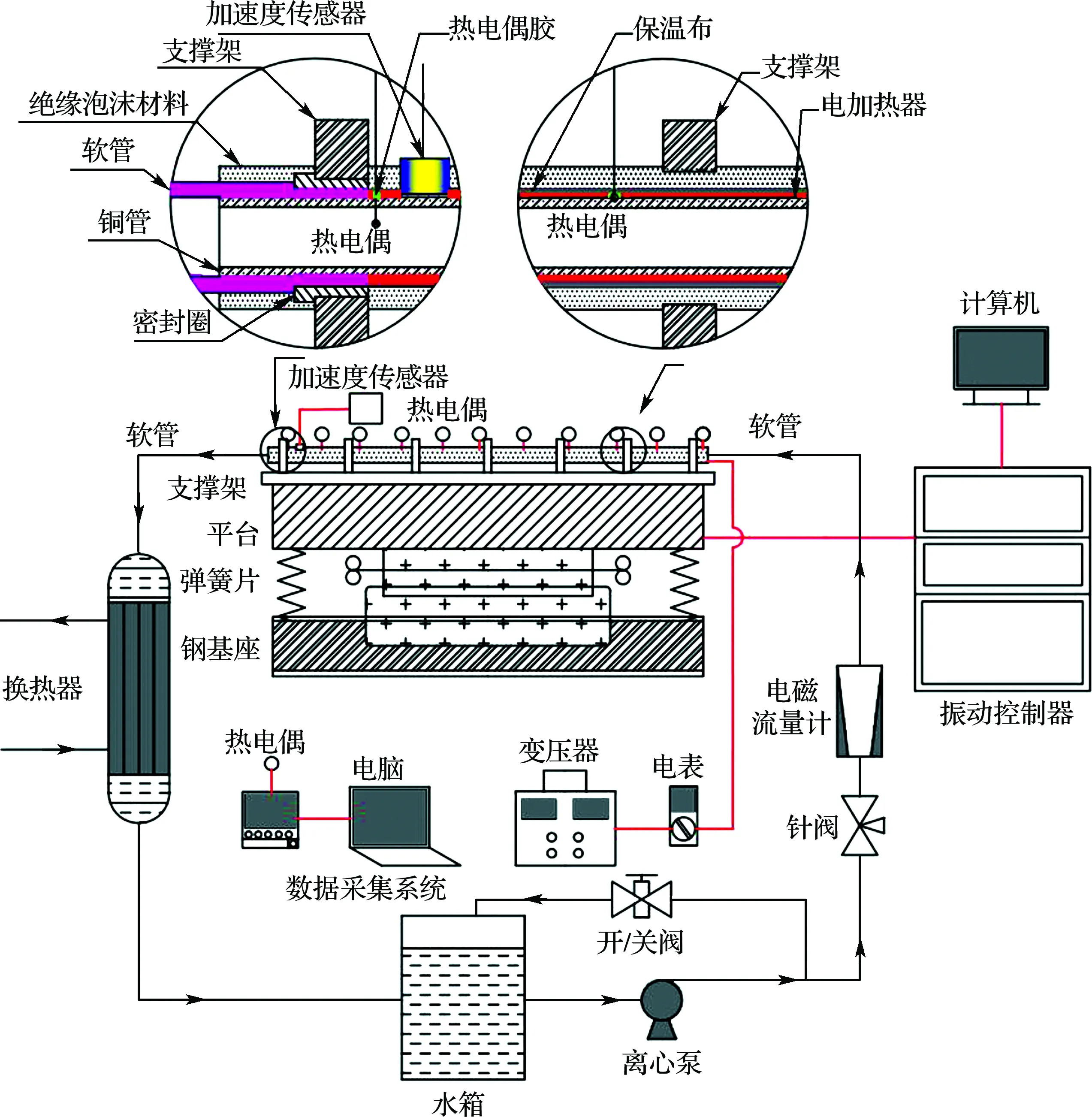
图1 实验系统示意图Fig.1 Schematic diagram of the experiment system

(2)振动部分

采用ES-10D-240型振动系统，可测量频率范围是5～5 000 Hz，最大加速度1 000g．该振动系统包含钢基座、弹簧片、振动器、振动台面及振动控制器．

(3)电加热部分

电加热部分采用35 Ω/m、直径3 mm的加热线均匀紧密缠绕在铜管上，用量程最大为250 V的直流电压调节器调节电压以改变加热功率，使用功率表测量功率．

(4)水循环系统部分

使用净化的蒸馏水作为循环介质，在实验段以外的部分，利用透明弹性软管进行连接，离心泵从水箱中抽取经过冷凝的常温水，使用针阀精确调节流体流量．

(5)振动加速度信号测量系统

利用PCB 208振动信号传感器测量振动加速度信号，经过过滤器和放大器后传入HP3567a型动态信号分析仪中进行处理，记录该信号．

(6)温度测量系统

温度测量系统包含测量进口和出口各1个液体温度测点，9个壁面温度测点，采用点式K型热电偶测量进出口液体温度，热电偶安装在液体中，壁面温度测点距离内壁面0.2 mm，温度数据采集使用YOKOGAWA HR1300记录仪，设置响应频率为1 Hz，可满足定频或定加速度的稳态振动记录需求．

针对本实验系统，首先进行不通水静态测试，测量烧空管情况下圆管的散热损失量；其次，进行通水静态实验，计算得到该条件下管内的对流换热系数；最后，启动振动控制器，分别改变振动频率、振动加速度和水的质量流量进行实验，采集不同实验条件下的温度信号．

1.2 实验数据处理

实验测量的主要参数有温度、流量、振动频率、振动加速度，通过数据采集系统实时将实验数据输入计算机．待实验工况稳定后，进行数据采集．

流体管内加热量为

(1)

管内对流换热系数：

(2)

Nusselt数：

Nu=hd/λ

(3)

流体雷诺数：

Re=udρ/μ

(4)

式中：Q为加热量，ρ为流体密度，d为圆管内径，cp为比定压热容，T″f为出口液体温度，T′f为进口液体温度，h为管内对流换热系数，A为圆管横截面积，u为流体速度，l为管长，λ为导热系数，μ为流体动力黏度．

由于实验过程中所测量的量具有误差，在进行雷诺数Re、管内对流换热系数h、加热量Q、Nu的计算时都具有一定的不确定度．间接测量的参数，往往受到直接测量误差的影响发生误差传递现象，假设间接测量量由有限个直接测量量决定：

F=f(x1+x2+…+xn)

(5)

直接测量量不确定度分别为U1，U2，…，Un，则相对不确定度为

(6)

根据以上方法，进行相关参数的误差分析．经计算得出，Re的不确定度为3.18%，Nu的不确定度为4.51%，h的不确定度为4.52%，热流密度q的不确定度为4.57%．

2 实验结果与讨论

2.1 散热损失公式拟合

散热损失可由流体的进出口温差和输入的电功率得出，亦可通过不通流体加热空管测量，本实验采用加热空管来计算散热损失．当管内为空时，由于空气的导热系数较小，进行通电加热，测量通电功率和测量管表面及环境温度的差值，绘制温差及通电功率之间的关系曲线，拟合相关关系式．当环境温度和壁面温度的差值ΔTaw一定时，就可以计算出散热损失．根据实验数据计算结果绘制如图2所示散热损失随温差的变化曲线．

图2 环境和壁面温差ΔTaw和散热损失Qloss的关系

Fig.2 The relationship of temperature difference ΔTawbetween wall and environment and heat lossQloss

散热损失和温差的拟合关系式如下式所示：

(7)

温差和散热损失公式拟合相关性为0.995 6．

2.2 静态管内流体传热实验验证

在进行振动实验之前，先进行管内流体传热的静态实验，本实验用圆管长为1 m，管内层流流动处于入口段范围，将本实验结果与Sieder等[11]和Bejan等[12]确定的层流入口段实验关联式进行对比，验证实验的准确性．

如图3所示，分别为Sieder等、Bejan等所做实验关联式所描述的曲线和本文实验测量值的曲线，本文实验值位于两个关联式所描述曲线之间，在相同Re情况下，本文实验所得Nu与两种关联式所得结果的最大偏差为22%，满足实验要求，静态实验的结果具有较高的可信度．

2.3 FFT圆管振动分析

快速傅里叶变换方法(FFT)在机械振动分析方面具有广泛的应用，可大大减少计算时间和复杂度．本文实验首先确定圆管在扫频条件下的瞬态动力特性，得到其振动加速度和时间的关系，然后根据加速度的时域信号，使用Matlab编写FFT方法的程序，将时域信号转换为频域信号，即得出振动频率和振动加速度之间的关系．其波形如图4所示．

图3 管内层流流动实验结果与实验关联式计算的Nu比较

Fig.3 Data verification ofNufor laminar flow in tube with those of correlations

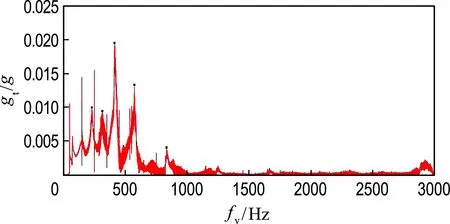
图4 经过FFT方法变换后的加速度频域信号Fig.4 Frequency domain signal of acceleration transferred by FFT methods

从图中可以看出，在频率变化的过程中振动加速度出现了多个峰值，频率为412 Hz左右时，振动加速度达到最大，说明此段为此谐波的共振频率范围．其余出现的峰值分别为二次、三次谐波的频率．振动加速度变化幅度较大的区域在0～1 000 Hz，因此，将该区域振动作用对传热的影响作为研究重点．

2.4 振动加速度gt、振动频率fv与圆管内对流换热系数间的关系

振动参数的改变和流体流速的变化会影响流体的传热性能．图5反映了不同振动频率、振动加速度在不同Re条件下Nu的变化情况．由图可知，4种Re条件下表现出相同的特性，即随着振动加速度的增大，Nu稍有增大；随着振动频率的增大，Nu先增大，到达一个峰值之后，出现下降的趋势，然后趋于平缓．

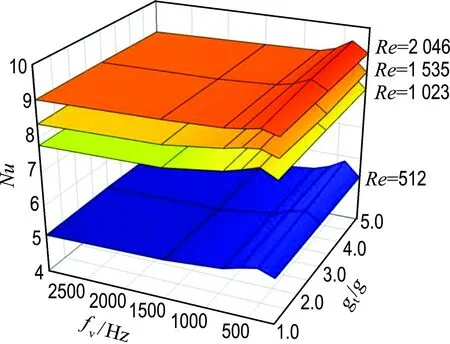
图5 振动频率、振动加速度以及Re与Nu间的关系

Fig.5 Overall preview ofNuas a function of vibration frequency, acceleration andRe

从现象上可大致得出：振动加速度对Nu的影响不及振动频率和Re的影响．共振频率对传热的影响很大．

图6为Re=512时，不同振动加速度下Nu随振动频率的变化规律．

图6Re=512，振动频率、振动加速度和Nu间的关系

Fig.6 The relationship between vibration frequency, acceleration andNuatRe=512

从图6中可以看出，振动加速度和振动频率都对传热特性产生很大的影响．随着振动频率的增大，Nu先增大，在400 Hz时达到最大，最大增加14.94%，然后迅速减小，到达1 500 Hz之后缓慢减小，最终趋于稳定．这主要是因为振动使圆管壁面附近的流体边界层发生扰动，进而改变热边界层的发展，传热效果得到改善．而随着频率的增大，振动愈加强烈，当达到共振频率时振动最强烈，对边界层的扰动最大，传热效果最好．此外，从图中也可看出，增强效果较为明显的频率区域为200～1 000 Hz．考虑振动加速度对传热的影响，随着振动加速度的增大，Nu增大，管内对流换热系数增强．如图6所示，5g条件下管内对流换热系数最大．此外，相对比测试段的振动加速度动态测量得出的共振频率为412.7 Hz，实验测试值400 Hz较接近于共振频率．

图7所示为振动加速度为3g时，不同Re下，Nu增强率随振幅变化的曲线．

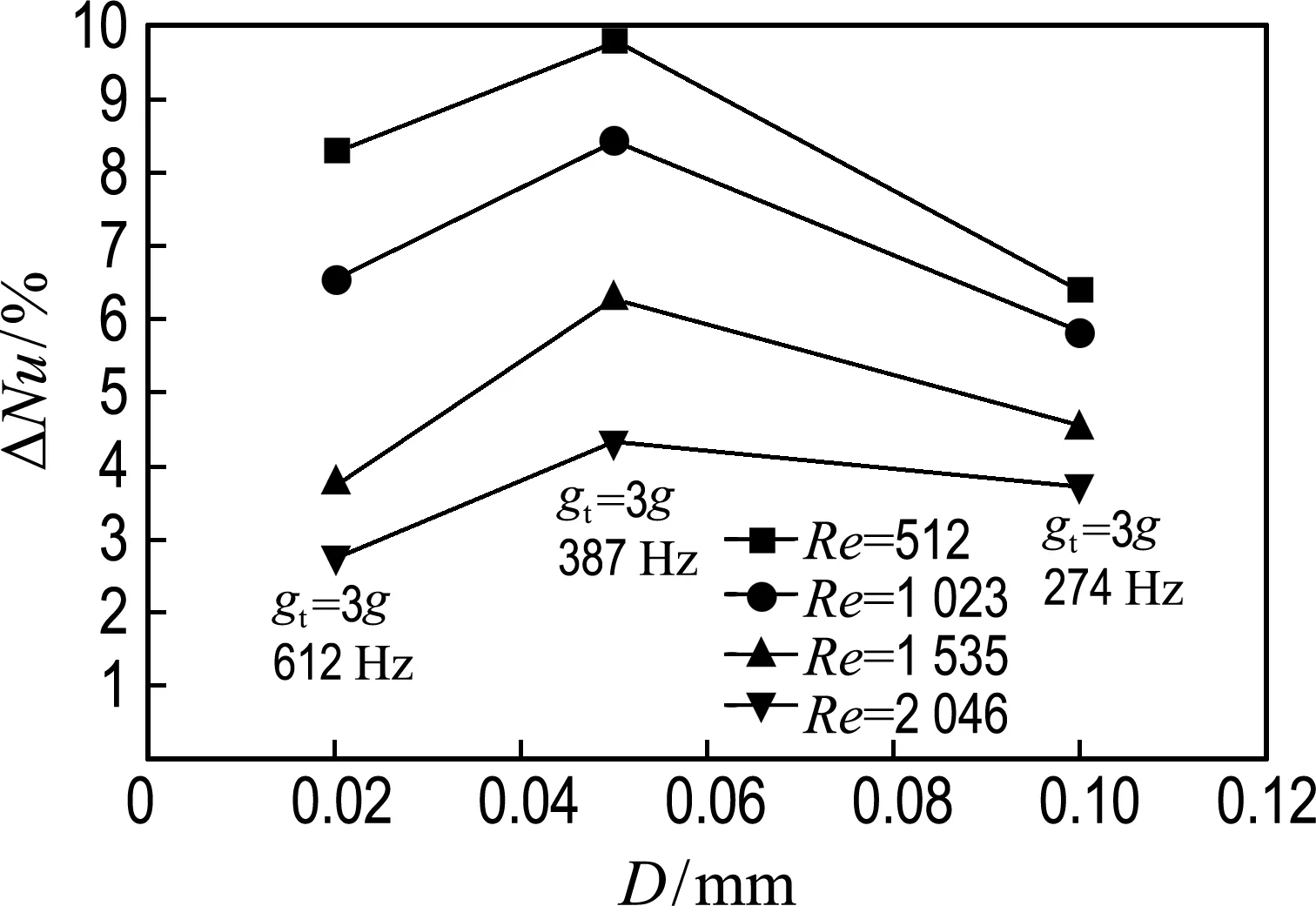
图7 振动加速度为3g时振幅D与ΔNu间的关系

Fig.7 The relationship between vibration displacementDand ΔNuat vibration accelerationgt=3g

从图中可以看出，随着管内流动Re的增大，Nu的增强率减小，振动对流体的流动有扰动作用，增强了管内液体的掺混，从而增强了流体与管内壁面间的换热，在小Re时，Nu增强效果较为明显．随着振幅的增大，Nu增强率先增大后减小．由于本实验的振幅较小，且对实验的影响无规律可循，对此没有进行更深入的探究．本文主要研究振动加速度、振动频率对传热的影响．

2.5 实验关联式拟合

本实验中，在频率为400 Hz时，振动作用对管内传热增强效果最好．与之后根据实验测量值计算得到的共振频率412.7 Hz相近，因此，取关联式中共振频率fn=400 Hz，需要拟合的Nu增强率与3个变量有关，ΔNu=F(gt，fv，Re)．根据实验所得数据拟合的关联式如下：

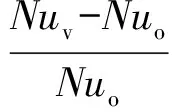
(8)

拟合得出

A=49.31，B=0.943，C=3.168，

Z=217.875，E=-0.525，fn=400 Hz

实验验证范围为

512≤Re≤2 047， 1g≤gt≤5g， 158 Hz≤fv≤3 000 Hz

数据拟合相关性系数为0.82，根据实验数据和关联式计算得出Nu误差率，如图8所示．

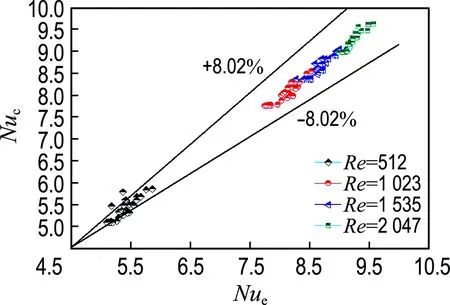
图8 Nu关联式所得结果与实验结果误差比较Fig.8 Experimentally Nusselt number vs calculated result from correlation

通过120组不同工况下的实验数据进行计算，将拟合公式得出的结果和实验结果进行比较，可以得出关联式的最大误差在8.02%附近，所拟合的关联式较好地吻合了实验结果．该实验关联式适用于高频低振幅管内层流流动，将会给工程应用提供有用的参考．

3 结 论

(1)计算了稳态情况下，管内层流流动对流换热Nu随Re的变化趋势，并将实验结果与前人的关联式结果进行了比较，偏差最大为22%．

(2)在高频低振幅条件下，振动频率对传热的影响强于振动加速度．随着振动频率的增大，Nu增大，当振动频率达到共振频率(本实验400 Hz)时，Nu增强率达到峰值14.94%；在定频条件下，Nu随着振动加速度的增大而增大；在较小的Re条件下，振动作用对传热的影响效果较为明显．

(3)根据实验数据拟合得到Nu增强率与振动频率fv、振动加速度gt、流动Re之间的关系式，与实验结果进行比较，Nu增强率的最大误差率为8.02%左右．该关联式可为相关工程应用提供参考．

[1] LEMLICH R. Effect of vibration on natural convective heat transfer [J].IndustrialandEngineeringChemistry, 1955,47(6):1175-1180.

[2]PENNEY W R, JEFFERSON T B. Heat transfer from an oscillating horizontal wire to water and ethylene glycol [J].JournalofHeatTransfer, 1966,88(4):359-363.

[3]HSIEH R, MARSTERS G F. Heat transfer from a vibrating vertical array of horizontal cylinders [J].TheCanadianJournalofChemicalEngineering, 1973,51(3):302-306.

[4]SAXENA U C, LAIRD A K. Heat transfer from a cylinder oscillating in a cross-flow [J].JournalofHeatTransfer, 1978,100(4):684-689.

[5]CHENG C H, CHEN H N, AUNG W. Experimental study of the effect of transverse oscillation on convection heat transfer from a circular cylinder [J].JournalofHeatTransfer—TransactionsoftheASME, 1997,119(3):474-482.

[6]SWANSON V H. The effect of oscillation and gas content on free convection from horizontal cylinders in water [D]. Corvallis: Oregon State University, 1962.

[7]GRAVES D L. Effect of vibration on forced convection to water from a cylinder at Reynolds numbers in the range of stable vortex shedding [D]. Corvallis: Oregon State University, 1964.

[8]SCANLAN J A. Effects of normal surface vibration on laminar forced convective heat transfer [J].IndustrialandEngineeringChemistry, 1958,50(10):1565-1568.

[9]SHI Junxiang, HU Jingwen, SCHAFER S R,etal. Numerical study of heat transfer enhancement of channel via vortex-induced vibration [J].AppliedThermalEngineering, 2014,70(1):838-845.

[10]吴艳阳,刘利军,喻九阳,等. 振动圆管内对流传热特性及场协同分析[J]. 石油化工设备, 2011,40(6):1-5.

WU Yanyang, LIU Lijun, YU Jiuyang,etal. Convective heat transfer characteristics and field synergy analysis inside vibration circular tube [J].Petro-ChemicalEquipment, 2011,40(6):1-5. (in Chinese)

[11]SIEDER E N, TATE G E. Heat transfer and pressure drop of liquids in tubes [J].Industrial&EngineeringChemistry, 1936,28(12):1429-1435.

[12]BEJAN A, KRAUS A D.HeatTransferHandbook[M]. New York: John Wiley & Sons, Inc., 2002.