关于柔性悬索桥主缆静力计算方法的探讨

■陈国柱

（广东中誉设计院有限公司，广州 511500）

1 前言

近年来，很多景区为增加游客游览的趣味性开始新建景观悬索桥。大多新建的悬索桥采用平面桁架的形式（即采用的不设置加劲梁或较小的加劲梁且梁高较小的桁架形式），采用该结构形式的悬索桥主梁刚度较小不能与主缆协同受力，使得该种类型的悬索桥受力情况有区别于刚性悬索桥（即有足够刚度加劲梁、主缆与加劲梁共同受力的超静定结构）而称之为柔性悬索桥。

2 项目概况

某人行景观柔性悬索桥，桥梁总长219m，设计荷载采用人群荷载P为3.0kPa。桥跨组合为（16.5+186+16.5）m，主跨长度L=186m，主缆矢高f=6m，矢跨比为S0=f/L=1/31，主缆间距 3.1m。 主缆采用 14根 Φ42（6×19+IWS）的 A类镀锌钢丝绳，单根主缆截面积19386.4mm2，钢丝绳标准强度1870MPa，弹性模量2.0×105MPa。抗风主缆由Φ42（6×37S+IWR）组成，每岸通过2根锚桩锚碇于两岸山坡岩体内。抗风拉索选用1Φ20（6×37S+IWR），A类镀锌标准。拉索通过抗风主缆和主梁上的转向滑轮形成受力的、大小不等的三角形从两侧绷紧主桥，抗风索主缆的初张力50kN，风缆与水平面夹角30°。人行道净宽2.5m，横梁间距3m，横梁采用采用]25c钢，纵梁采用]14b钢，桥面板采用规格为5mm厚钢板桥面板，人行道系采用4.5cm厚防腐木。本桥全桥采用不设置吊杆的上承式受力形式。由于受地形限制，主缆通过高度较小的转向墩转到锚碇方向，故不设置桥塔，主缆在主跨方向倾角为φ=7.24°，边跨方向倾角为φ=20°。桥梁锚碇采用隧道和锚碇板的组合式锚碇形式，主缆与锚碇板间的通过拉杆及灌锌铜铝合金套筒进行连接。桥型布置图详见图1。

图1 桥型布置图（单位：cm）

2 计算方法

本文采用弹性理论和有限位移理论，以及几何非线性分析方法进行计算分析。

2.1 弹性理论方法的基本假定

弹性理论方法是基于以下假定条件：

（1）假定主缆为完全柔性，吊杆沿跨密布。

（2）假定主缆曲线状态和纵坐标在加载后保持不变。

（3）加劲梁沿跨径悬挂在主缆上，其截面的惯性矩沿跨不变。

（4）一般加劲梁是在主缆和吊杆安装完毕后才分段吊装就位，最后连成整体，所以加劲梁等恒重已由主缆承担，加劲梁中仅有活载、风力和温度变化产生的内力。

2.2 有限位移理论方法的基本假定

有限位移理论方法基于以下假定条件：

（1）全部应力在比例极限以下。

（2）各杆件为等截面。

（3）材料服从胡克定律。

（4）结构无面外屈曲。

（5）钢缆及吊杆完全为柔性。

（6）荷载集中于节点。

2.3 几何非线性分析方法

结构在大位移工况下，当结构的变形影响结构刚度时，采用线性理论进行结构内力求解求得的结果将出现较大的偏差。几何非线性分析方法是用全拉格朗日列式法（T.L列式法）或修正拉格朗日列式法（U.L列式法）建立有限元方程，采用增量法或迭代法（Newton-Raphson）求出结构在平衡状态的结构内力，以解决结构在大位移影响结构刚度时的内力求解问题。

2.4 弹性理论方法与有限位移理论方法计算柔性悬索桥的差别

采用弹性理论方法计算柔性悬索桥时，需把柔性悬索桥假定为静定或超静定结构，然后采用结构力学的方法求解内力；需要把加劲梁假定为等截面的梁。

有限位移理论则只是在材料强度容许值内对结构不存在面内结构屈曲及面外结构失稳进行了假定，计算柔性悬索桥内力时用几何非线性分析计算。

在实际工程中，柔性悬索桥在外加均布荷载工况下主缆将出现下挠，下挠数值呈现主跨跨中最大，越靠近桥塔挠度越小；在半跨偏载工况下，加载侧主缆下挠，未加载侧主缆上拱，并伴随着顺桥向位移，主缆呈现S型；在半幅偏载工况下，由于加劲梁刚度及自重较小，主缆在加载侧挠度较大，未加载侧挠度较小，横桥向将出现横坡。在外加荷载作用下，几何非线性特征明显，因此认为有限位移理论方法进行几何非线性分析得出的计算结果比弹性理论方法得出的计算结果更接近于实际情况。

3 静力分析

3.1 计算参数

（1）主索：Φ42mm，单位重 7.037kg/m，单侧 14 根全桥28 根， 单根长 186.51m。 总重：2×14×186.51×7.37=38488kg≈384.88kN

（2）索夹：10615.7kg≈106.15kN

（3）横梁：][25C 槽钢，单位重 70.5 kg/m，根数 62根，单根长度3.7m；横梁缀板：320×224×30钢板，单根横梁34.5kg；224×220×10 钢板，单根横梁 39.3 kg。 总重：70.5×62×3.7+62×（34.5+39.3）=20748.3kg≈207.4kN

（4）［14b 纵梁：单位重 16.73 kg/m，根数 3 根，单根长186.51m。 总重：3×16.73×186.51=9360.9kg≈93.61kN

（5）踢脚梁

侧板：1000×140×10mm，单位重 11 kg/m，根数 4 根，单根长度186.51m；面板：1000×183×10mm单位重 14.4 kg/m，根数 2 根，单根长度 186.51m。 总重：4×186.51×11+2×186.51×14.4=13577.9kg≈135.779kN

（6）桥面板：2500×1000×5mm 花纹钢板，单位重98.125kg/m,根数1根，单根长度186.51m。总重量：98.125×186.51=18301.3kg≈183kN

（7）桥面铺装：2500×1000×45mm 防腐木板，单位重61.88kg/m,根数1根，单根长度186.51m；40×100mm防腐木龙骨，单位重 2.2kg/m,根数5根，单根长度 186.51m；L56×36×5 角钢，单位重 3.47kg/m，根数 3660 根，单根长度 0.2m。总重量：61.88×186.51+5×2.2×186.51+3660×3.47×0.2=16132kg≈161.3kN

（8）全桥栏杆总重：18492.4kg≈184.92kN

（9）风缆（含拉索及抗风主缆）： 4267kg≈42.6kN

（10）平衡索：6058.1kg≈60.58kN

（11）主桥恒载总重：

384.88 +106.15+207.4+93.61+135.779+183+161.3+184.92+42.6+60.58≈1550.2kN

恒载每延米重g=1550.2/186≈8.3kN/m

3.2 采用弹性理论方法进行静力分析

3.2.1 主缆内力计算

（1）恒载作用下单根主缆水平拉力Hg：

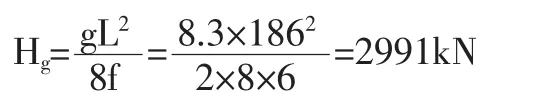
（2）人群荷载作用下单根主缆水平拉力 ：

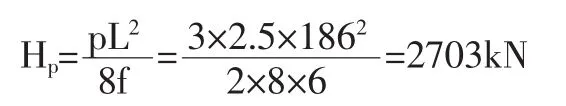
（3）单根主缆水平内力标准组合 H（g+p）：

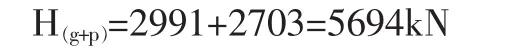
（4）主索鞍处的最大内力 Tp+g：

主跨方向（取主跨向水平夹角7.24°）

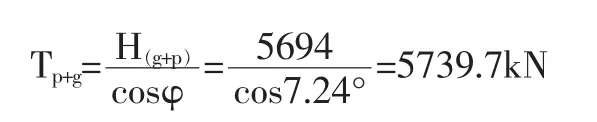
边跨方向（取主跨向水平夹角20°）

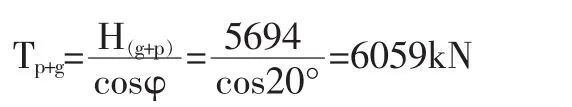
3.3 采用有限位移理论方法进行几何非线性静力分析

结构的计算分析采用“Midas/Civil 2015”有限元程序进行空间静力分析。钢梁、转向墩采用梁单元模拟，主缆及风缆采用索单元模拟。边界条件：转向桩基底及地锚处采用完全固结；桩基侧采用土弹簧进行模拟（X、Y向）；主缆与转向墩之间采用刚性连接。

计算过程中，采用倒拆法进行模型建立，采用Newton-Raphson法进行迭代计算，控制位移收敛精度为1mm。先采用全桥恒载均摊至主缆进行初步找型得出主缆在恒载作用下的刚度及初始平衡状态，再建立桥梁的其他构件进行精确平衡。在建模过程中，做到每个施工阶段都收敛，最终得到成桥状态的精确平衡。计算模型见图2。主缆成桥坐标图见图3。

图2 计算模型

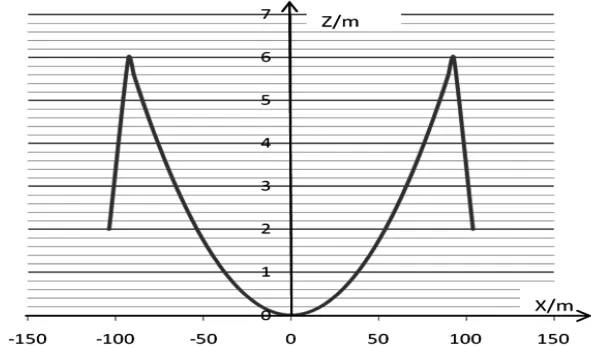
图3 主缆成桥坐标图

为分析有限位移理论方法与弹性理论方法的区别，本次分析计算采用三个工况：工况一只考虑恒载作用时主缆内力；工况二只考虑人群作用时主缆内力；工况三同时考虑恒载和人群荷载作用时主缆的内力。

3.3.1 工况一：只考虑恒载作用时主缆内力

只考虑恒载作用时，主缆最大内力为边跨方向，单根主缆内力为3216kN。恒载作用下主缆内力见图4。

3.3.2 工况二：只考虑人群作用时主缆内力

只考虑人群作用（全桥满人荷载3kPa）时，主缆最大内力为边跨方向，单根主缆内力为2715kN。人群荷载作用下主缆内力见图5。

图4 恒载作用下主缆内力图

3.3.3 工况三：同时考虑恒载和人群荷载作用时主缆的内力。

同时考虑恒载和人群荷载作用 （全桥满人荷载3kPa）时，主缆最大内力为边跨方向，单根主缆内力为4447kN。恒载和人群荷载共同作用下主缆内力见图6。

图5 人群荷载作用下主缆内力图

图6 恒载和人群荷载共同作用下主缆内力图

4 计算结果分析

4.1 计算结果汇总

三种方法内力计算结果汇总表，见表1。

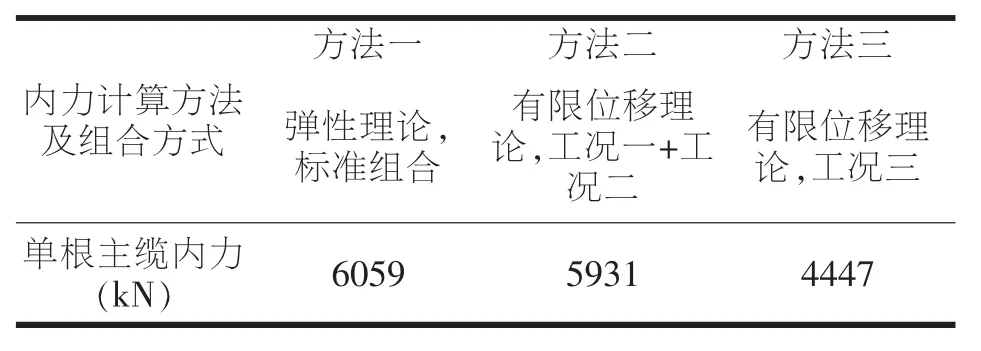
表1 计算结果汇总表

4.2 计算结果比较

现以计算方法一（即弹性理论，标准组合）作为参照，对三种计算方法结果进行比较结果如下表2：

表2 计算结果对比表

4.3 对比结论分析

计算方法一与计算方法二计算结果差值在3%范围内，在结构可靠度允许误差范围内，计算结果基本一致，判定计算模型无误。计算方法三与计算方法一进行比较，主缆内力较方法一小26.6%。

鉴于柔性悬索桥为几何非线性结构，在外加荷载作用下整体结构变形较大。采用弹性理论方法计算或有限位移理论进行几何非线性分析计算后线性叠加未考虑活载作用产生位移引起的内力重新分配对主缆的影响等诸多因素，依据主缆内力公式当增加时主缆内力将减小。采用有限位移理论进行几何非线性分析计算方法在以永久作用确定结构刚度后，再计算各种可变作用的效应，这可以有效的减少可变荷载作用下对主缆内力的影响，得到更精确的计算结果。分析认为计算方法三得出的计算结果较接近实际，更精确；计算方法一、二得出的计算结果偏于安全。

5 结语

弹性理论计算方法采用人工计算较为便捷，能快速的得出计算结果，计算结果精度一般，但在工程可行性研究报告、方案设计或初步设计阶段完全能满足精度要求。采用有限位移理论进行几何非线性分析计算，计算结果较为精确。由于采用人工计算工作量较为繁重，在计算机技术迅猛发展的今天，采用计算机代替人工计算也能较快的得到计算结果，特别是施工图设计阶段采用该计算方法将取得较好的精确效果。

[1]徐君兰.桥梁计算示例集-吊桥.北京：人民交通出版社，1991.

[2]周远棣,徐君兰.钢桥.北京：人民交通出版社，2003.

[3]程翔云.桥梁设计与计算.北京：人民交通出版社，2007.

[4]中华人民共和国交通运输部.JTG/T d65-05-2015,公路悬索桥设计规范[S].北京：人民交通出版社股份有限公司，2015.

[5]宋迎军.大跨径吊桥的静力特性与动力特性分析[J].交通建设与管理,2015（04）.