山西西里北铁矿矿体资源储量估算中斜楔形体积公式的应用

2018-03-21朱明海

现代矿业 2018年2期

郭旻朱明海

(五矿矿业(安徽)工程设计有限公司)

在固体矿产勘查过程中，最重要的工作是进行矿产资源储量估算，由于矿床的多样性和矿体形态的复杂性，使得勘查方法多种多样，相应的资源储量估算方法也种类繁多[1-5]。传统的估算方法主要有几何法和统计分析法[6-9]，几何法应用相对较广[10]。几何法是将形态复杂的矿体描绘成与该矿体体积大致相等的几何形体，利用简单的数学公式计算其体积，利用体积与矿石平均体积体重来估算资源储量，主要方法有垂直断面法、平行断面法、块段法等[11-14]。在采用垂直断面法时，采用的体积计算公式主要有梯形体积公式、截锥体积公式、锥形体积公式和楔形体积公式。本研究发现，对于既不作锥形尖灭，也不作楔形尖灭的矿体，仅采用锥形体积公式和楔形体积公式对块段体积进行估算，易存在偏差。本研究以山西省临汾市西里北铁矿为例，采用斜楔形体积公式估算资源量，以提高矿体块段资源储量估算的准确性。

1 矿床地质特征

西里北铁矿位于华北地台南缘，秦岭—大别山活动带北缘[15-16]。矿区地表大部分被第四系覆盖，仅在矿区东部出露二叠系上统石千峰组长石砂岩。二叠系下统下石盒子组泥岩、细砂岩、粉砂岩，上统上石盒子组粉砂岩、细砂岩；石炭系上统山西组泥页岩、太原组长石石英砂岩；奥陶系中统峰峰组薄层—厚层灰岩、上马家沟组泥质灰岩、泥灰岩等地层仅在钻孔有揭露。矿区地表仅在南部发育一条压性正断层，深部由钻孔控制，断层倾角为70°～80°，穿过二叠系地层。矿区内地表岩浆岩仅在北部出露巨斑正长岩，深部主要为闪长岩、辉石二长闪长玢岩，均属燕山期产物，侵位于奥陶系下统下马家沟组顶部至二叠系上统石千峰组[15]。岩体侵位形成似背型隆起，走向为NE向，在与灰岩的接触带内形成了接触交代型磁铁矿床，成为矿区成矿母岩。矿床为中型隐伏接触交代型磁铁矿床，矿体产于燕山期闪长玢岩与奥陶系中统灰岩的接触带上。由于受岩体与灰岩接触带控制，矿体分层明显，总体呈似层状产出，空间上表现为波状起伏[15]。目前，矿区自上而下圈定了4个矿体，编号分别为Ⅰ#、Ⅱ#、Ⅲ#、Ⅳ#，各矿体的形态特征见表1。

表1 西里北铁矿矿体特征[15，17]

2 资源储量估算

2.1 斜楔形体块段几何形态及体积计算公式

同一块段的2相邻剖面(1个剖面为有效面积，另1个剖面为无效面积(面积为0))即可构成斜楔形体块段[18]，斜楔形体几何形态见图1。

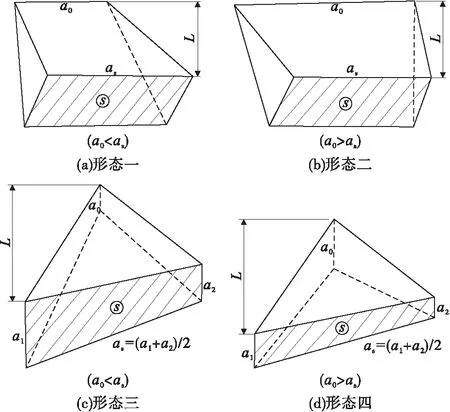
图1 斜楔形体几何形态

斜楔形体积计算公式为

式中，V为矿体块段体积，m3；a0为无效面积尖灭长度或矿层厚度，m；as为有效面积的对应边长或有效断面之平均矿层厚度，m；S为有效断面面积，m2；L为线距或外推距离，m。

2.2 斜楔形体积公式的应用

西里北铁矿存在诸多斜楔形体矿块，故而不宜笼统地采用楔形公式或锥形公式进行资源储量估算，本研究采用斜楔形体积公式进行资源储量估算。该铁矿主矿体的资源储量估算平面如图2所示。由图2可知：Ⅰ#矿体中涉及的斜楔形体块段主要为332-3、333-1、333-4、333-5、333-6、333-7，Ⅱ#矿体中涉及的斜楔形体块段主要为332-1、333-1、333-5、333-6；Ⅲ#矿体中涉及的斜楔形体块段主要为332-1、332-2、332-3、332-4、333-1、333-10；Ⅳ#矿体中涉及的斜楔形体块段主要为332-1、332-4、333-1、333-10。上述斜楔形体的资源储量估算结果见表2。

3 讨论

3.1 斜楔形体积计算公式的应用条件

(1)当矿体沿走向或倾向作无限外推时(如本研究矿床中各矿体中333级别块段)，外推块段体积应采用斜楔形体积公式进行计算。

(2)当1个剖面有2个或2个以上工程控制，另1个剖面有1个工程控制时，如本研究各矿体中332级别块段体积宜采用斜楔形体积公式进行计算。

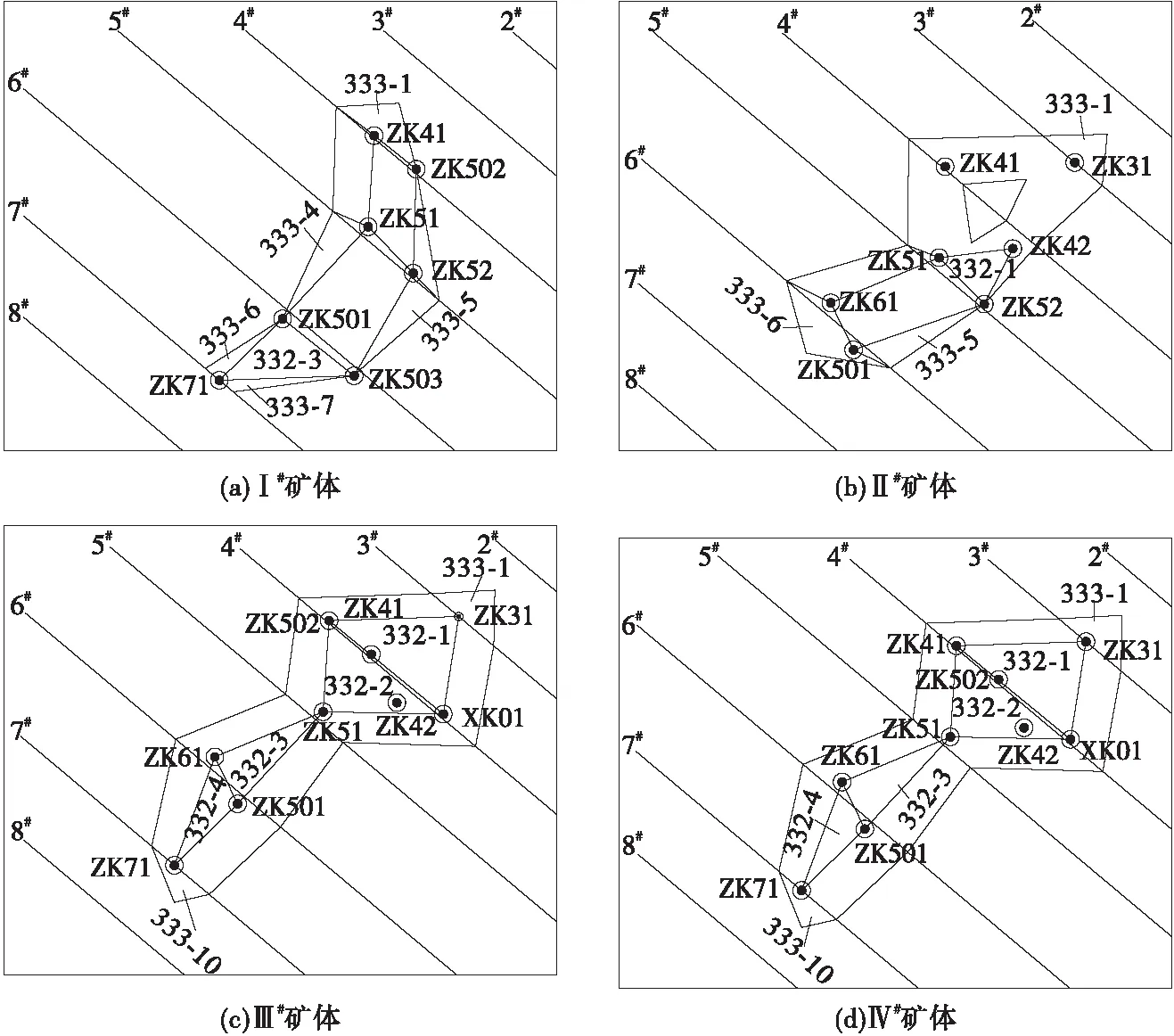
图2 西里北铁矿各矿体资源储量估算水平投影

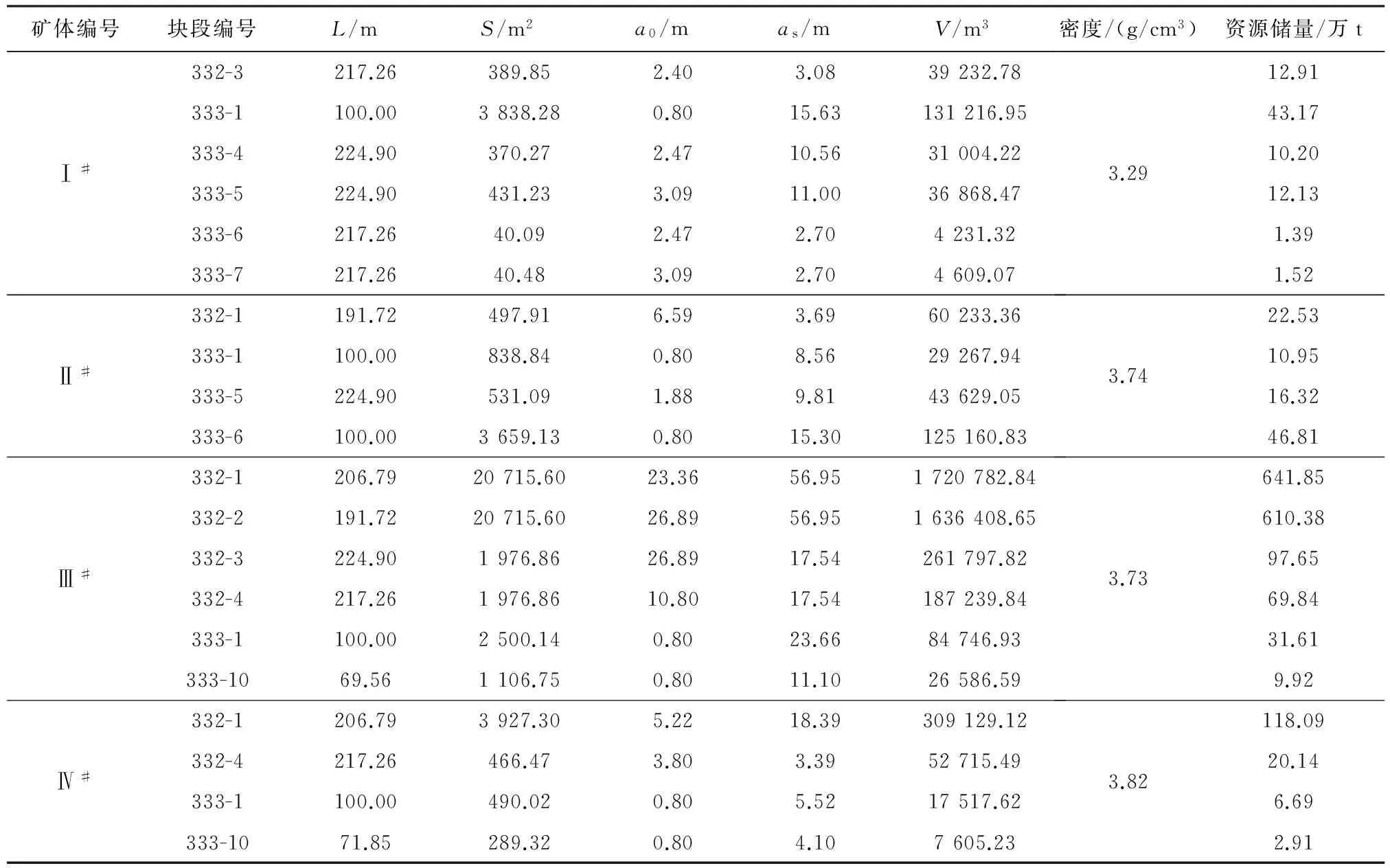
表2 西里北铁矿斜楔形体块段资源储量估算结果

3.2 斜楔形体积公式验证

当无效面积呈直线a0尖灭，而a0小于有效面积对应的块体厚度as(图3(a))时，可将图3(a)中EF延长至G点，使得EG=as，则FG=as-a0，则块段体积计算公式即为本研究斜楔形体积计算公式。

当无效面积呈直线a0尖灭，而a0大于有效面积对应块体厚度as(图3(b))时，斜楔形体积公式仍可采用上式进行计算。

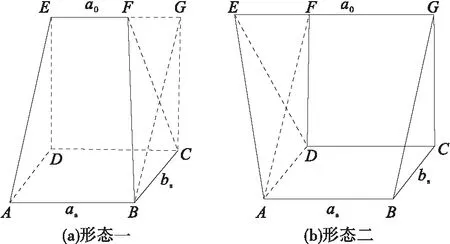
图3 斜楔形体形态

当a0=0时，则V=L·S/3，即为锥形体积公式；当a0=as时，即为楔形体积公式。由此可知，对于同一块段的2相邻剖面，1个剖面为有效面积，另1个剖面为无效面积(面积为0)时，斜楔形体积公式具有普遍意义，锥形体积公式和楔形体积公式仅为斜楔形体积公式的特例。

4 结语

分析了山西省临汾市西里北铁矿的矿床地质特征，并采用斜楔形体积公式估算了主要矿体各矿段的资源储量，在此基础上进一步分析了该公式的应用条件。研究表明，在资源储量估算中，常使用的锥形体积公式和楔形体积公式仅为斜楔形体积公式的2个特例，应用斜楔形体积公式对于提高矿体部分特殊块段资源储量估算的合理性及准确性有一定的实际意义。

[1] 曹建洲，赵远由，谢环宇.地质块段法在固体矿产资源储量估算的应用探讨[J].矿产勘查，2015，6(4)：466-470.

[2] 袁勇，王志龙.储量计算克立格法与SD法的对比分析[J].内蒙古石油化工，2009，35(4)：42-43.

[3] 刘晓明，吕太含冰，陈建宏，等.基于地质统计学的资源储量估算参数优选研究[J].矿冶工程，2015，35(2)：23-28.

[4] 马爱玲.矿产资源储量估算方法SD法与传统几何法之差异[J].科技与企业，2011(8)：22-24.

[5] 白瑞和.固体矿产资源储量计算方法的探讨[J].中国非金属矿工业导刊，2010(6)：59-61.

[6] 王建文，郑焜曦，秦海.基于矿体垂直纵投影地质块段法的矿产资源储量估算[J].内蒙古煤炭经济，2013(5)：107-108.

[7] 赵增玉，潘懋，田甜，等.固体矿产资源储量估算系统中垂直断面法的实现[J].地质与勘探，2010，46(3)：547-552.

[8] 王小丹，王标，牛水源.常用资源储量估算方法的对比分析[J].四川有色金属，2015(2)：5-7.

[9] 张灼，依龙静，王靖文.矿产资源储量简化计算法[J].矿业工程，2015，13(1)：42-43.

[10] 李守义，叶松青.矿产勘查学[M].北京：地质出版社，2003.

[11] 杨金富，周仕雄，薛力鹏.基于DIMINE的会理拉拉铜矿三维地质建模及储量估算[J].金属矿山，2016(8)：114-118.

[12] 汪昌亮.印度尼西亚某金矿矿体三维实体建模及资源量估算[J].现代矿业，2016(2)：136-147.