The value of dual mean Minksowski measure of symmetry at the critical Minkowski points of a convex body
2018-03-21LIUJianguoGUOQi
LIU Jianguo,GUO Qi
(School of Mathematics and Physics,SUST,Suzhou 215009,China)
1 Introduction
Let C⊂Rn(the n-dimensional Euclidean space) be a convex body(i.e.a compact convex set with non-empty interior).Denote bythe determining family of C,i.e.[1]

One of the important geometric invariants of convex bodies,the Minkowski measure function of asymmetry as∞(·),is defined by

where “int” denotes the interior(the definition of this form is from[1],see[2-4]for other equivalent definitions),and the Minkowski measure of asymmetry as∞(C) of C is so defined as
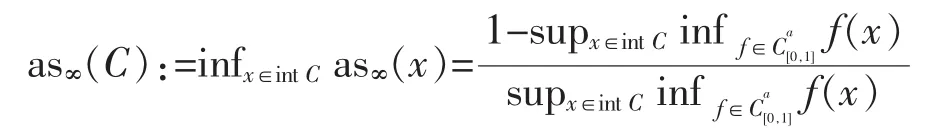
A point x*∈int C such that as∞(x*)=as∞(C) is called a ∞-critical point (or Minkowski-critical point by other authors).The set of all∞-points of C is called the ∞-critical set of C,denoted by C∞,which is a nonempty closed convex subset of C[2-3].Given x*∈C∞,an f*∈Ca[0,1]satisfying f*(x*) =intf∈Caf(x*) (in turn as∞(C)=[0,1](1-f*(x*))/f*(x*)) is called a critical function of C with respect to x*(w.r.t.for brevity).Denote by C*∞(x*) the set of critical functions of C w.r.t.x*(in general C*∞(x*) varies as x*varies).Observe that,for any f*∈C*∞(x*),

There are numerous generalizations,extensions of the Minkowski measures (see[8-11]and the references therein),among which Toth's work in[6],Guo and Toth's work in[7]are of particular value.The measures they defined provide information not only for the convex bodies themselves but also for their low dimensional sections or orthogonal projections.
Given a convex body C∈Kn(the family of convex bodies),for each m≥1,we call a multi-set{f0,…,fm}⊂Ca[0,1](repetitions are allowed) an m-support configuration of C i{fi≤0}=Ø,where{fi≤0}:={x∈Rn|fi(x)≤0}.The family of m-support configurations of C is denoted byEom=ECo,m.Then we have the following definition[7,12].
Definition 1Let C∈Kn.For m≥1,its m-th dual mean Minkowski measure fucntionint C→Ris defined by
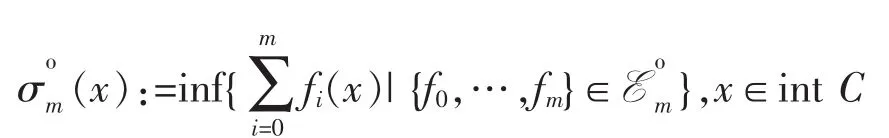
A point x*∈int C satisfyingis called a σom-critical point of C.Denote by Comthe set of-critical points of C.It is easy to check that Comis a closed convex subset of C[7].
Both ∞-critical points and σon-critical points are of some interesting properties[3,13].So it is meaningful to provide methods in finding these critical points.There are already some practical criterions for detecting the∞-critical points,however,there are not many for the σom-critical points.Fortunately,some clues lead to a Conjec-ture:for any C∈Kn,
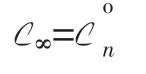
This conjecture is still open.One of the important steps for confirming this conjecture is to find the precise value of σonat the ∞-critical points.So,in this paper,we give explicit value of σonat the∞-critical points in terms of the Minkowski measure of asymmetry.
For notation and terms unmentioned above we refer to[14-15].
2 Critical n-support configurations
In this section,we focus on the nth dual mean Minkowski measures and show the existence of some particular n-support configurations.
Definition 2Let C∈Knand x*∈C∞.If{f0,…,fn}∈Eonsatisfies fi∈C*∞(x*),then{f0,…,fn}is called a critical n-support configuration of C (w.r.t.x*).
The following is the main result of this section.
Theorem 1Let C∈Kn.For each x*∈C∞,there is at least one critical n-support configuration w.r.t.x*.
To prove Theorem 1,some more preparations are needed.First,we rewrite (3.1) and (3.2) in[3]as one lemma with our notation.
Lemma 1[3]Let C∈Knand x*∈C∞.Then
To see Lemma 1 is indeed equivalent to (3.1) and (3.2) in[3],one needs only to observe that a closed half space G belongs to the family W appearing in[3]iff G={f≤0}for some f∈C*∞(x*).
Then,we show a theorem of Helly's type for families of half spaces,which,besides being needed in the proof of Theorem 1,is of its own significance.Some notation and terminologies first:recall that a function f:Rn→Ris affine iff there is a unique (u,b)∈Rn×Rsuch that f(·)=〈u,·〉+b and that f is invertible iff u≠o,where “o” denotes the origin or zero vector.A family{fi}i∈Λwith fi(·)=〈ui,·〉+bi,where Λ is any nonempty index set,is called compact if{(ui,b)}i∈Λis compact inRn×R.
Theorem 2Given C∈Kn.Let{fi=〈ui,·〉+bi}i∈Λ⊂Ca[0,1]be compact.Then,the following statements are equivalent:
(2)For each u∈Rn,〈ui,u〉≤0 for some i∈Λ.
(3)The origin o∈ri(conv{ui0,…,uil}for some afinely independent ui0,…,uil,1≤l≤n,i.e.,there are positive
(4)cone{ui0,…,uil}=lin{ui0,…,uil}for some afinely independent ui0,…,uil,1≤l≤n.
Lemma 2Let fi(·)=〈ui,·〉+bi,i=0,1,…,m be non-trivial affine functions.Then,for any (um+1,bm+1)∈cone{(u0,b0),…,(um,bm)},we have
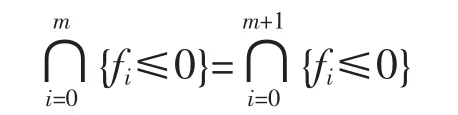
Proof.,then the equality is obvious.If,then this is just a reformulation of the well-known generalized Farkas lemma[15].
Proof of Theorem 2We point out first that{(ui,bi)}i∈Λ⊂Rn×Ris compact iff both {ui}⊂Rnand{bi}⊂R are compact.
(2) ⇒ (3):Consider the linear space V:=cone{ui}i∈Λ∩(-cone{ui}i∈Λ).If V={0},then by the separation theorem for closed cones (cone{ui}i∈Λis closed since{ui}i∈Λis compact),there is u∈Rnsuch that{ui}i∈Λ∈{x|〈u,x〉>0},which contradicts (2).So dimV≥1.Now,it's easy to see by induction that V=cone{ui0,…,uis}for some ui0,…,uis(1≤s≤n).
Thus,since-ui0∈lin{uis}sk=0=cone{uis}sk=0,we have-ui0=α0′ui0+,which leads to o=We now let l be the smallest positive integer such that

for some ui0,…,uilwith αik>0 and claim that ui0,…,uilare affinely independent.Suppose ui0,…,uilare not affinely independent,thenfor some (not all zero) βi0,…,βilwith
2.1.1 磷酸氢二钾用量对多酚提取率的影响 在磷酸氢二钾乙醇双水相中,下相由溶解后的磷酸氢二钾及少量乙醇构成,上相则由乙醇和水构成,易溶于乙醇相的多酚提取出后进入上相.双水相的形成是磷酸氢二钾与乙醇争夺水分子的过程.随着磷酸氢二钾用量的增加,盐对水的束缚能力增强,使上相中乙醇的相对体积分数增加[5].从图2可以看出,随着磷酸氢二钾用量的增加,总多酚得率先上升后下降,磷酸氢二钾过少,双水相萃取能力低,磷酸氢二钾过多导致多酚进入下相造成损失;在磷酸氢二钾2.5 g时,多酚的提取率达到最高值.
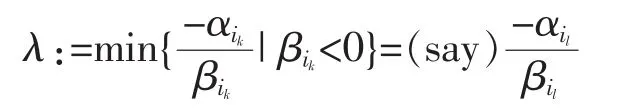
then
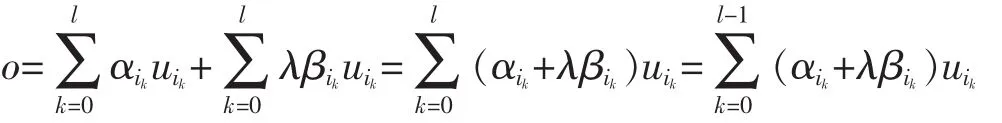
where αik+λβik≥0,(0≤k≤l-1),and at least one of them is positive,a contradiction to the choice of l.It follows from (**) that

l≤n clearly since ui0,…,uilare affinely independent.
(3)⇒(4):Suppose that ui0,…,uil,l≤n,are affinely independent and 0∈ri(conv{ui0,…,uil}),i.e.,with αik>0.Then for each 0≤k≤l,we have-uikuij∈cone{ui0,…,uil}.Thus lin{ui0,…,uil}=cone{ui0,…,uil}.
(4)⇒(1):Suppose lin{ui0,…,uil}=cone{ui0,…,uil}with affinely independent ui0,…,uilfor some 1≤l≤n,with at least one αijpositive.Thus,settingby Lemma 2 we have

where we used the fact that{fi0≤0}∩{fil+1≤0}=Ø since{fil+1≤0}⊂{fi0>0}which follows from that
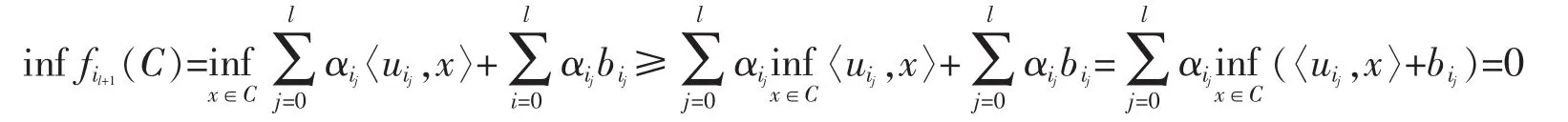
Lemma 3Let C∈Knand x*∈C∞.Then both Ca[0,1]and C*∞(x*) are compactly located.
Proof.It was shown that Ca[0,1]is compact (Lemma 1 in[1]).So we need only to show that C*∞(x*) is closed.Let the sequenceThen f∈Ca[0,1]by the closedness of Ca[0,1]and which implies f∈C*∞(x*)and so C*∞(x*)is closed.
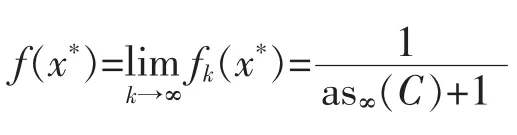
Proof of Theorem 1First,by Lemma 1,Then,since C*∞(x*) is compact by Lemma 3,the origin o∈ri(conv{ui0,…,uil}) for some affinely independent ui0,…,uil,1≤l≤n by (1)⇒(3) in Theorem 2,where fij(·):=〈uij,·〉+bij∈C*∞(x*) for some bij∈R.Now,by applying (3)⇒(1) in Theorem 2 to the family{fij}lj=0,we haveObserving l≤n,we finally obtainfor any fil+1,fil+2,…,fin∈C*∞(x*),i.e.{fi0,…,fil,fil+1,…,fin}is a critical n-support configuration.
3 Main theorem and its proof
In this section,we present our main result:
Theorem 3Let C∈Knand x*∈C∞.Then we have
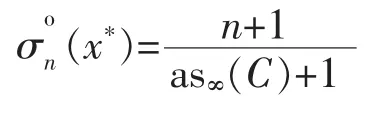
Proof.On one hand,for any n-support configuration{f0,f1,…,fn}∈Eon,fixing an f*∈C*∞(x*),we have by(*) in Section 1,
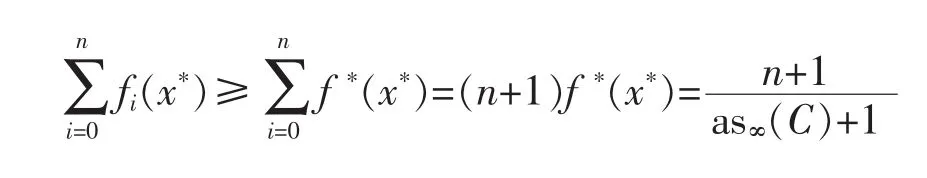
Thus
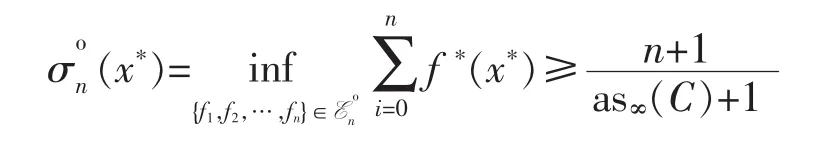
On the other hand,there is a critical n-support configuration{f0*,f1*,…,fn*}by Theorem 2.Thus we have
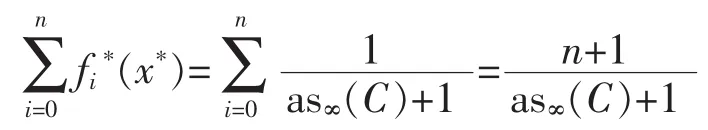

[1]GUO Q.Stability of the Minkowski measure of asym
[2]GRÜNBAUM B.Measures of symmetry for convex set[J].Convexity Proceedings of Symposia in Pure Mathematics,1963,7:233-270.
[3]KLEE V L.The critical set of a convex set[J].Amer J Math,1953,75:178-188.
[4]GUO Q,KAIJSER S.On asymmetry of some convex bodies[J].Discrete Comput Geom,2002,27:239-247.
[5]HIRIART-URRUTY J B,LEMARÉCHAL C.Fundamentals of Convex Analysis[M].Berling-Heidelberg-New York:Springer Verlag,2001.
[6]TOTH G.Simplicial intersections of a convex set and moduli for spherical minimal immersions[J].The MichiganMathematical Journal,2004,52(2):341-359.
[7]GUO Q,TOTH G.Dual mean Minkowski measures of symmetry for convex bodies[J].Science China:Mathematics,2016,59(7):1383-1394.
[8]TOTH G.Measures of symmetry for Convex Sets and Stability[M].New York:Springer,2015.
[9]GUO Q.On p-measures of asymmetry for convex bodies[J].Adv Geom,2012,12:287-301.
[10]GROEMER H.Stability theorems for two measures of symmetry[J].Discrete Comput Geom,2000,24:301-311.
[11]GROEMER H,WALLEN L J.A measure of asymmetry for domains of constant width[J].Beitrage Algebra Geom,2001,42:517-521.
[12]YAO D,GUO Q.Measures of asymmetry dual to mean Minkowski measures of asymmetry for convex bodies[J].Comm Math Res,2016,32(3):207-216.
[13]GUO Q,TOTH G.Dual mean Minkowski measures and the Grüunbaum conjecture for affine diameters[J].Pacific Journal of Mathematics,2018,292(1):117-137.
[14]SCHNEIDER R.Convex Bodies:The Brunn-Minkowski Theory[M].2th ed.Cambridge:Cambridge University Press,2014.
[15]HIRIART-URRUTY J B,LEMARÉCHAL C.Fundamentals of Convex Analysis[M].New York:Springer Verlag,2001.
