The graph polynomials and their equivalence
2018-03-21PENGYanling
PENG Yanling
(School of Mathematics and Physics,SUST,Suzhou 215009,China)
1 Introduction
A graph G=(V(G),E(G)) is given by the set of vertices V(G) and a symmetric edge-relation E(G).We denote by n(G) the number of vertices,and by m(G) the number of edges[1-2].Graph polynomials are graph invariants with values in a polynomial ring,usually Z[X]with X=(X1,…,Xr).
The first graph polynomial,the chromatic polynomial,was introduced in 1912 by G.Birkhoff to study the Four Color Conjecture.Later on R.C.Read did research on chromatic polynomial deeply and got many important results[3].The characteristic polynomial[4]and the matching polynomial[5]were introduced with applications from chemistry[6-7].These graph polynomials are studied for various reasons[8]:graph polynomials can be used to distinguish non-isomorphic graphs;new graph polynomials are used to model the behavior of physical,chemical or biological systems.In this paper,we introduce these graph polynomials and the equivalence of these graph polynomials.Meanwhile,we discuss the connections between these graph polynomials and give some examples about equivalence of these graph polynomials.
2 Graph polynomial
In this section we introduce some graph polynomials and discuss the connections between them.
Definition 1[9]Let G be a graph with n vertices,λ be the number of colours of colouring the vertices of G,c(G,k) denote the number of distinct colour-partitions of V(G) into k colour-classes,and (λ)kbe the number of ways of choosing the colors.The chromatic polynomial of G is the function defined by

where (λ)k=λ(λ-1)(λ-2)…(λ-k+1).
Some simple properties of the chromatic polynomial follow directly from its definition.For example,if G has n vertices,then the coefficient of λnis 1;hence P(G;λ) is a monic polynomial of degree n.
The chromatic polynomial P(G;λ)=c(G,k)(λ)kcan be expressed as follows

Proposition 1[9]Let G be a graph of girth g,having m edges and η cycles of length g.Then,with the above notation for the coefficients of the chromatic polynomial of G,we have
The coefficients in the above chromatic polynomial relate to the structure of a graph.For example,the coefficcient b1is-m,where m is the number of edges of G.
Definition 2[10]Let G be a graph with n vertices.A k-matching in a graph G is a set of k edges,no two of which have a vertex in common.The number of k-matchings in G will be denoted by m(G,k).We set m(G,0)=1 and define the matching polynomial of G by

Remark 1If we put x=y,then we get the following polynomial

which is called the simple matching polynomial.
Remark 2There are several versions of the univariate matching polynomial such as the matching defect polynomial and the matching generating polynomial(see Example 2).
Theorem 1(λ)kbe the chromatic polynomial of the complement of G and be the simple matching polynomial of G.Then a(G,k)=m(G,k)if G is triangle free.
Proof.Since m(G,k) is the number of matchings of G with k components,and a(G,k)is the number of color partitions of G with k color-classes,we need to prove that,when G is triangle free,for each matching of G with k components,there exists an unique color partition of G with k color-classes,and vice versa.
Observe that a matching in G is a spanning subgraph of G,each of whose components consists of a single edge or a single vertex.Now,for each component in a k-matching of G,we have a color class of two vertices or one vertex in a k color-partition of G.Therefore,for each matching of G with k components,there exists a unique k color-partition of G.Conversely,since G is triangle free,for an arbitrary k color-partition of G,each color class of this partition contains no more than two vertices.Therefore,for each color class in a k color-partition of G,we have a single edge or a single vertex in a k-matching of G.i.e.for each color-partition of G with k color-classes,there exists a unique matching of G with k components.So,a(G,k)=m(G,k).
Remark 3Theorem 1 gives a link between the chromatic polynomial and the matching polynomial.
Definition 3[9]Let A be the n×n adjacency matrix of graph G.The characteristic polynomial det(λI-A)will be referred to as the characteristic polynomial of G,and denoted by χ(G;λ).
Proposition 2[10]Then the coefficients of λn-rare given by

where the summation is over all elementary subgraphs γ of G with r vertices.An elementary graph is a simple graph,each component of which is regular and has degree 1 or 2.Comp(γ) is the number of components in γ and cyc(γ) is the number of cycles in γ.
The characteristic polynomial of a graph is an algebraic construction which contains graphical information.For example,a1=0,-a2is the number of edges of G,-a3is twice the number of triangles in G,and a4=na-2nb,where nais the number of pairs of disjoint edges in G,and nbis the number of 4-cycles in G.
Lemma 1[9]Suppose that Σciλn-iis the characteristic polynomial of a tree with n vertices.Then the odd coefficients c2r+1are zero,and the even coefficients c2rare given by the rule that(-1)rc2ris the number of ways of choosing r disjoint edges in the tree.
By this lemma,it is easy to get the connection between the characteristic polynomial and matching polynomial,as shown in the following theorem.
Theorem 2Let Σciλn-ibe the characteristic polynomial of G and μ(G;x)m(G,k)xn-kbe the matchings polynomial of G.If G is a forest,then (-1)rc2r= m(G,r).
3 Equivalence of graph polynomials
In this section we introduce the equivalence of graph polynomials and give some examples about equivalence of graph polynomials.
Definition 4[11]Two graphs G1and G2are called similar if they have the same number of vertices,edges and connected components.
Definition 5[11]Two graph polynomials P(G;X1,…,Xr) and Q(G;Y1,…,Ys) are equivalent in distinctive power (d.p.-equivalent) if for every two similar graphs G1and G2we have

iff

Definition 6[11]Let P and Q be two graph polynomials.
(ⅰ)P is more distinctive than Q,Q≾d.p.P if for all pairs of similar graphs G1,G2with Q(G1)=Q(G2) we also have P(G1)=P(G2);
(ⅱ)P and Q are d.p.-equivalent or equally distinctive,P~d.p.Q,if both Q≾d.p.P and P≾d.p.Q hold.
Next,we will give some examples of equivalent graph polynomials.
Example 1Let P(G;x) be the chromatic polynomial of graph G with integer coefficients and

where X(i)is the falling factorial function X(i)=X(X-1)…(X-i+1).We denote by ai,biand cithe coefficients of these polynomials and by zithe roots of these polynomials with their multiplicities.We note that the four presentations of the chromatic polynomial P(G;x) are all d.p.-equivalent.
Example 2Let μ(G;x) be the matching defect polynomial

and g(G;X) be the matching generating polynomial
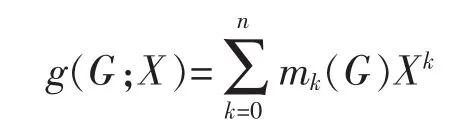
Then,it is easy to get μ(G;x)=Xng(G;(-X-2)).It follows that g(G;X) and μ(G;x) are equally distinctive.
[1]BOLLOBÁS B.Modern Graph Theory[M].Berlin:Springer,1998.
[2]BONDY J A,Murty U S R.Graph Theory with Applications[M].London:Macmil-lan Press LTD,1976.
[3]READ R C.An introduction to chromatic polynomials[J].J Combinatorial Theory,1968,4:52-71.[4]BROUWER A E,HAEMERS W H.Spectra of Graphs[M].New York:Springer Univeristext,2012.
[5]LOVÁSZ L,PLUMMER M D.Matching theory[J].Annals of Discrete Mathematics,1986,29:121-142.
[6]BALABAN A T.Solved and unsolved problems in chemical graph theory[J].Ann Discrete Math,1993,35:109-126.
[7]TRINAJSTIC N,Chemical Graph Theory[M].2th ed.Boca Raton:CRC Press,1992.
[8]SOKAL A D.Bounds on the complex zeros of chromatic polynomials and Potts-model partition functions[J].Combin Probab Comput,2001,10:41-77.
[9]BIGGS N.Algebraic Graph Theory[M].Cambridge:Cambridge University Press,1993.
[10]GODSIL C D.Algebraic Combinatorics[M].New York:Chapman&Hall,1993.
[11]MAKOWSKY J A,RAVVE E V,BLANACARD N K.On the location of roots of graph polynomials[J].European Journal of Combinatorics,2014,41:1-19.
