基于改进t-Copula模型的一篮子信用违约互换定价研究

周士元

（1.复旦大学 应用经济学博士后流动站，上海 200433；2.河南大学 战略管理研究所，河南 开封 475004）

0 问题的提出

随着全球金融市场与金融产品创新的进一步细化，金融风险在金融投资主体间转移逐渐成为一种趋向。信用违约互换定价规模自2006年以来呈现逐步上升趋势，并且一直保持快速的增长。2010年10月，银行间货币市场交易商协会发布的信用风险缓释工具相关指引，标志着中国版CDS信用衍生产品市场正式启动，有利地助推了信用风险的释放。信用违约互换定价作为金融信用衍生品的一种，使风险资产的信用风险可以与资产所有权分离，转移信用风险的市场化安排使风险资产具有了流动性的特征，在银行信贷组合管理和上市企业金融风险控制方面发挥了重要作用。因此，如何进一步利用一篮子信用违约互换定价为上市企业提供金融风险的预期定价值规避渠道，具有一定的研究意义。

现有研究[1-6]主要侧重于信用违约互换定价的应用及应用方法，研究重点主要集中在利用一定的样本检测Copula模型的信用违约互换定价的适用性。但对于如何利用Copula模型进行进一步的时序分析有所不足。为此，本文按照时序节点分解不同程度的上市公司一篮子信用互换定价信息，结合信用违约行为与周边观测点的耦合互动，针对一篮子信用违约互换定价进行排列优化，来进一步验证上市公司一篮子信用违约互换定价基于时序改进Copula模型的应用精确性。

1 t-Copula模型设定与修正

1.1 Copula基本模型

假定上市企业个体样本对应的n个样本参照的违约时间分布在各个时序点，考虑到直接用联合分布函数很难直接表达上市公司一篮子信用违约互换定价的内部因子，因此通过Copula方法进行解决。Copula方法主要是通过向已知边际分布函数构建Copula函数，来解决违约时间矩阵元素以向量集的方式获得。

按照Copula原理，需要在构建过程中形成变量与时序节点在矩阵元素中的逻辑映射。而上市公司一篮子信用违约互换定价在时间节点中的定价分位数正好符合这一要求，从而使得定价问题变成一个基础Copula模型的分位数元素对称矩阵问题。由此，随机变量进行的随机分布函数假设符合Copula方法的逆函数特征，这一特征确保了一篮子信用违约互换定价能够顺利实现预测。具体过程如下。

按照上市企业在不同时序内的募股筹资行为进行违约时间的分点切割。即通过每一个矩阵元素对应的时序点映射一篮子信用违约行为，并从资产、收益率、随机变量等角度设置相应变量序列，再通过上述序列设定联合分布：

其中，τ1，τ2，...，τn分别对应为随机变量结构的转换系数，负责刻画上市公司一篮子信用违约互换定价在矩阵元素量向Copula模型间的转化程度；同时，鉴于上市公司一篮子信用违约互换定价过程是一个信息互换过程，必然包含上市公司经营所面临的共同经济影响，以及时序Copula验证中的时序特征。由此，获得t-Copula模型在整个验证过程中的测度效应系数为：

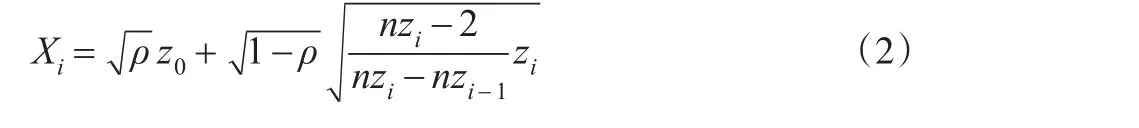
式（2）中，zn随机变量负责刻画的是上市公司一篮子信用违约互换定价形成价格向量集信息，再根据其是否符合标准正态分布函数集Φ(·)，进一步按独立同分布构造一个随机变量集，即 z1，z2，...，zn；由于上市公司一篮子信用违约存在定价不稳定价格线，也即是相应的随机分布特征，用分布函数测度不同于传统随机向量集的定价信息分布情形，即：

nzi负责描述基于上市公司一篮子信用违约背景下的随机变量自由度，也就是当一个随机变量落入定价预先设定的定价范围时，随机变量表现出的正向信息，否则表现出负向信息，即：

1.2 t-Copula模型修正

考虑到一个样本观测点实施的违约行为有可能与周边观测点形成相互影响的信用违约互换定价耦合的情形，本文主要从上市公司一篮子信用协议的视角进行了基于式（5）的排列优化。从排列中寻找适合上市公司的基准信用违约定价的趋势区间特征，从而突出每一个信用违约互换时间节点向平滑数列趋近的曲线特性，再从中找出关联规律。这里主要按照上市公司每一个发生一篮子信用违约互换定价行为的时间节点进行降序排列，并重新以全排列数据进行分布函数发生时，式（4）所对应时间节点的累积，即：

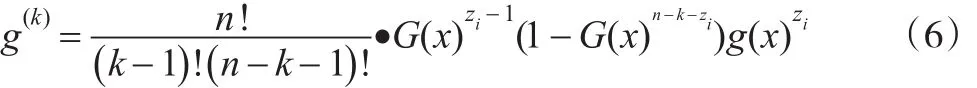
由此可以引出遍布整个统计分析时序内的连续违约分布函数，其对应的连续统计量为 τ1，τ2，...，τn。此时形成了具有联系样本分析意义的分布函数：

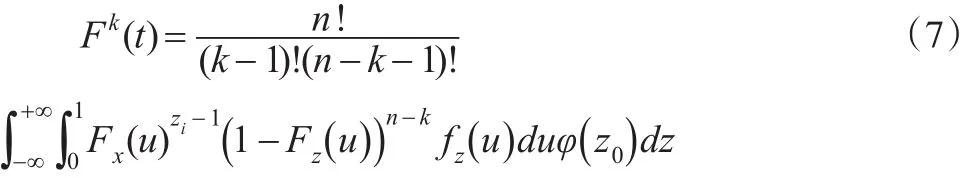
1.3 参数估计

根据上述分析，得到上市公司组合资产在不同时序节点形成一篮子信用违约实践的联合分布：

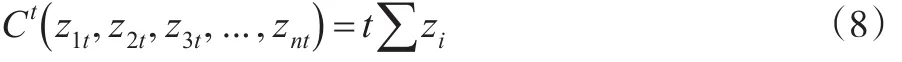
式（8）主要描述的是按照平滑向量集构成的连续函数，而每一个发生信用违约互换定价的行为都构成了上述连续函数的变量。由此，该组连续函数描绘的联合分布具备针对上市公司一篮子信用违约互换定价行为特征的描述能力。当然，需要进一步考虑在对上市公司进行定价行为预测时的多资产组合特性对预计价格范围的影响。本文将上述关于平滑向量机构成的连续函数以反函数的形式，实施密度函数分布的进一步解析，具体过程如下。

首先，将连续分布函数中的每一个节点作为测度向量集的矩阵构成元素，每个元素主要描述的是形成更为加密的、平滑的上市公司一篮子信用违约互换定价节点价格信息。由此可以结合式（2）、式（6）进行相应的矩阵转化。在结合每一个信用违约互换定价生成时的单分布作为单变量，其反函数按照表示为：

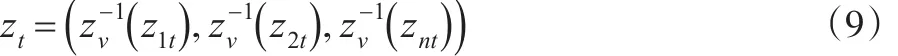
按照独立同分布视角筛选上述符合上市公司一篮子信用违约互换定价反函数单一序列的信号元素，并将其重新组合比较，构建出组合联合分布；再以z1t对应的第一段联合函数为基础，进行对应全时序阶段的验证，获得

；由这一参数逐次累计、结合正态分布样本进行相关系数的确定性验证，获得对应的后置一阶参变量系数；从而进一步细化上市公司一篮子信用违约实践与行为之间的逻辑关联。由此可以获得面向上市公司一篮子信用违约互换定价Copula模型相关联参数矩阵：

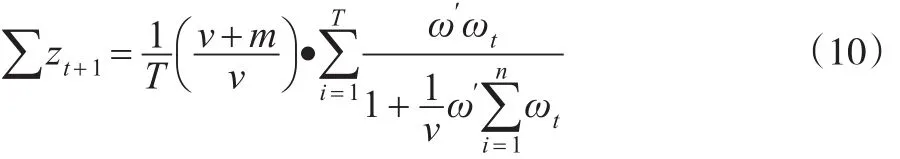
其次，将上市公司一篮子信用违约互换定价进行数值折算，即通过密度函数概率值。结合式（10）进行相应的折算，具体过程如下。

按照违约定价行为确定联合概率位于概率函数预期定价之外的边界。假定zi作为一个向量基础单元接触预期定价边界ui，然后结合式（4）进行相应的概率测算。

按照定义对应的参变量集中在一个可预测集τi，作为评估上市公司在一个特定时序内获得一篮子信用违约互换定价是否落入预期价格的范围。同时，按照可预测集的可控范围修正上述信用违约互换定价的偏离程度，即：

式（11）作为可控范围，测定对应的违约定价时间。并按照每一个可预测集τi逐步构建各个样本点对应的上市公司一篮子信用违约互换定价联合概率，由此可以获得对应上述偏离程度的评估集。该集合是对所有上市公司一篮子信用违约互换定价行为的偏离程度估计总集合。经过集合评估，形成对应随机变量的概率函数，并满足如下分段函数条件：

由此可以建立其每一种样本对应的随机分布函数在不同时序节点形成的上市公司一篮子信用违约互换定价的违约时间。用违约概率函数表示，即：

那么，按照每一个上市公司样本点分别进行前述改进Copula函数违约时间测度，即：

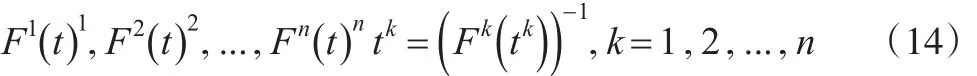
最后，重复上述步骤，对照式（11），形成一组对应顺序的一篮子信用违约互换定价预期时间随机概率组合。

2 实证分析

2.1 数据与指标

本文从2009年1月5日至2015年7月4日交易样本提取数据，按照对应统计时序获取共计2341个样本点数据。同时按照是否被ST将所有样本分为两大组别，即安全组别与非安全组别。检验数据主要源自上述上市公司的季度财务报表中涉及的股权结构、流动负债比、长期负债比、每股净资产收益等指标。

2.2 描述性统计

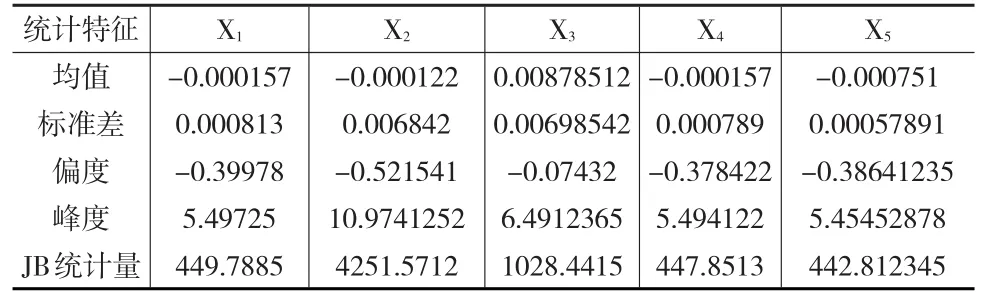
表1 数据描述性统计分析

从表1中可以发现，所选指标的均值偏度均不为零，且其对应的峰度超过了5，表现出数据样本显著的尖峰厚尾局部样本特征。而其中，第二个指标的JB统计量表明其显著地拒绝正态性分布假设。为此，针对上述样本进行了平稳性与独立性检验。首先进行相应的样本序列单位根ADF检验，结果如表2所示。整体而言，表中数据反映所选样本表现出基于时序Copula模型的平稳序列适应性。另外，也可以从表中数据反映的结果看出，样本均为非独立分布，其对应的上市企业在一篮子信用违约互换定价出现抽样的集聚现象，不存在样本点随机分布，可以进行进一步的一篮子信用违约互换定价验证。

2.3 单个样本的一篮子信用违约时间测度

根据上文分析，针对每一个密度函数对应的上市公司一篮子信用违约互换定价进行了时间节点的测度。按照样本点是否发生违约作为测度信号，进行基于泊松变化过程的强度评估，再按累积指数进行相应的分布函数测度，即：

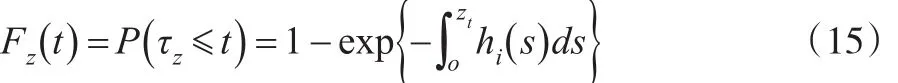
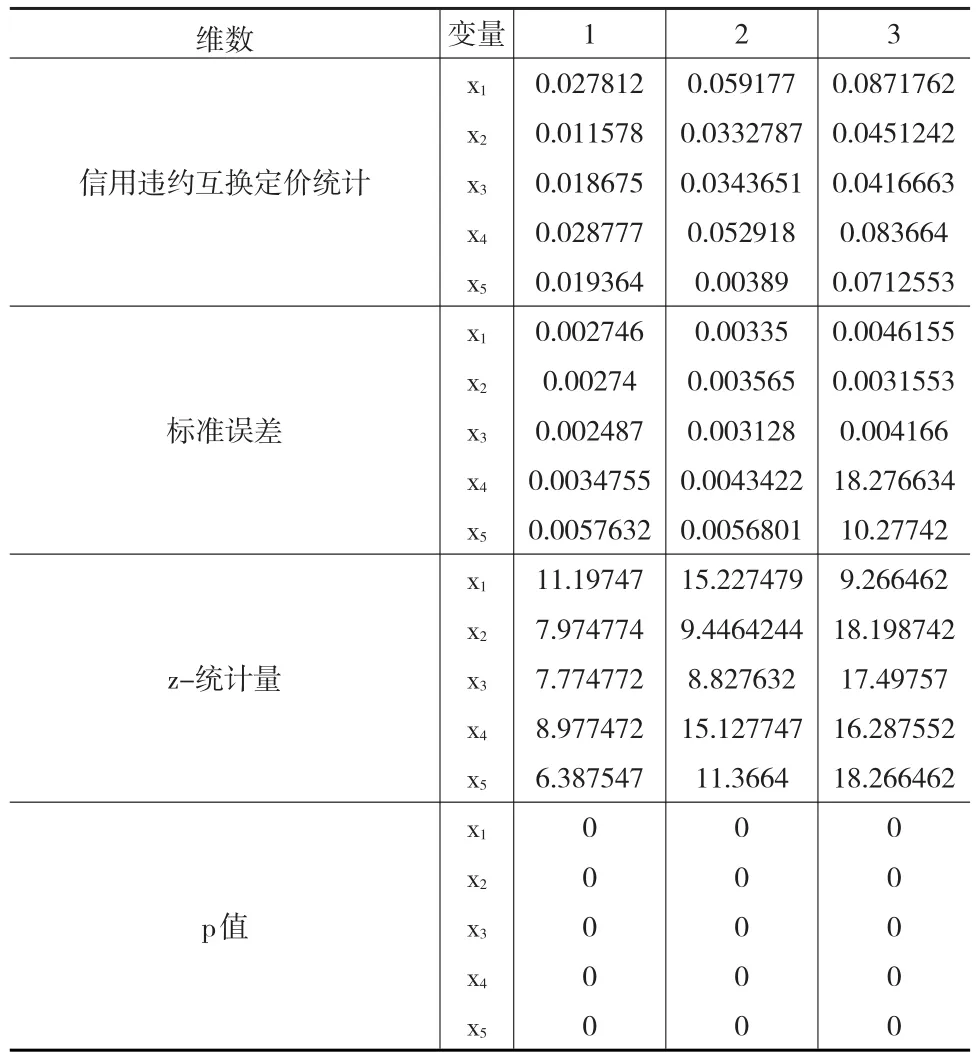
表2 信用违约互换定价copula序列检验

式（15）利用Copula模型进行了面向统计样本的期望，并将自初始期到第i个时序变化期内的联合违约概率作为期望基本变量；同时利用τz控制每一个落入预期价格区间的上市公司一篮子信用违约互换定价信号，即τz≤t，以此形成的总期望概率进行不同程度的上市公司一篮子信用联合违约行为所对应的不同分布函数验证。

按照每一组联合违约对应的一维变量进行修正Copula关联验证。假定每一个节点对应的输入量是一个联合违约概率的基本参变量，则基于式（11）改进的联合违约概率可以表示为：

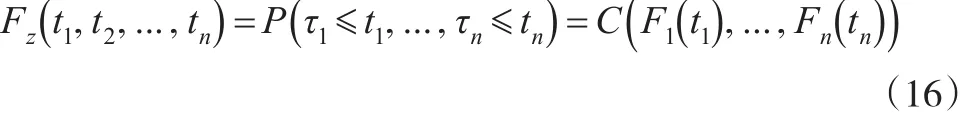
考虑到现阶段我国上市公司一篮子信用违约互换定价行为处于相对普遍的情形，按照不同程度映射的定价利率所反映的节点市场利率不同，可以通过不同节点市场利率映射上市公司一篮子信用违约互换定价行为波动，并利用微分将其进一步节点利率测度，从而简化上市公司一篮子信用违约互换定价行为，即：

由于Copula模式能够获得面向有序随机联合违约概率的节点利率波动，由此影响模型对于t-Copula在不同时序节点的验证表现。而此时，利用各组样本中对应节点的无风险利率可以采集上市公司一篮子信用违约互换定价行为中符合设定预期利率的部分，从而获得相应与其利用范围内的利率对应节点比例。

从下页图1可以看出，我国上市公司一篮子信用违约互换定价经历了3～5年显著性最为突出的利率对应节点比例波动，说明3～5年是上市公司进行一篮子信用违约预期定价波动频率最高的时序节点。

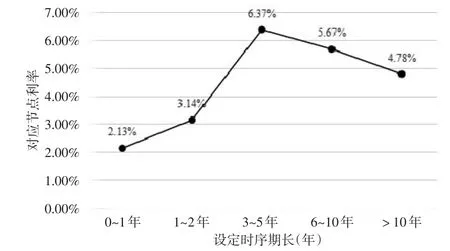
图1 上市公司一篮子信用违约互换定价经历

0～1年作为上市公司一篮子信用违约互换定价相对而言，其相关行为对应的信用违约互换定价相对不足。

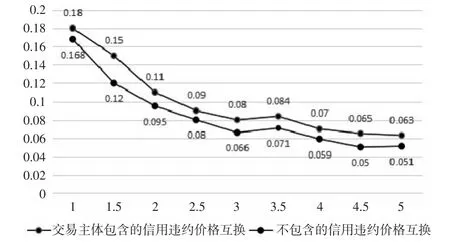
图2 上市公司一篮子信用违约互换定价分析

从图2中可以看出，无论是包含交易主体，还是不包含交易主体的t-Copula模型改进，上市公司一篮子信用违约互换定价都基本保持类似的走向趋势。还可以看出，经过时序修正的t-Copula模型解决了一个类似发展频率的两类上市公司一篮子信用违约互换定价行为，具有较长期限的测度精度的难题。同时，第三年的验证结果与先前验证的基本符合，此时，上市公司一篮子信用违约互换定价的交易样本6.37%节点利率。而相应的，基于时序Copula改进的上市公司一篮子信用违约互换定价分别是0.08和0.066，说明按照不同节点利率进行的信用违约互换定价相对集中，适合于3年期预期定价实践。

2.4 基于违约频次的一篮子信用违约互换定价解

本文结合选取样本以及节点利率和一篮子信用违约互换定价节点适应期限，利用社会统计软件SPSS12.0进行以3年为代表的上市债券验证。其面值设定为1个单位，每组变量的随机违约信号样本回收率为45%，而包含交易主体的信用违约利率报告为3.1%，设定频率仍然为0.5自然年。由此可以获得以基点为利率的对应违约价格信号组，具体如表3所示。

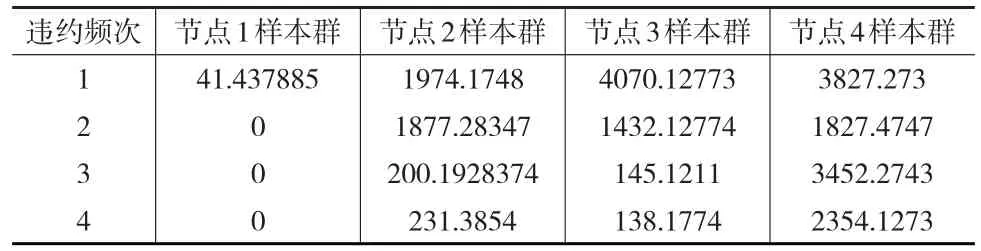
表3 基于违约频次的t-Copula模型对节点样本群信用违约互换定价的影响

从表3中可以看出，位于第一频次的信用违约互换定价的显著高频发生在第三节点样本群；而相比之下，样本所对应的节点样本群较其他样本具有更高违约频次，比此背景下的稳定互换定价影响显著性衰减。此时，节点四对应的是2～2.5年，因此，经过违约频次的t-Copula模型对节点样本群信用违约互换定价，相比原先的包含交易主体或不含交易主体的t-Copula模型测度结果提前了。由此可知，上市企业在今后的信用位于互换定价中应该逐步加强为以2年为监管周期的风险控制；而在实施信用违约互换定价实践中，应该逐步将互换定价的前期实践风险控制延展至3～3.5的周期。这样不仅有助于前移上市公司交易主体间互换定价的风险控制，还能进一步拓展非交易主体在交易环境和信用违约互换定价信号充沛的环境下，获得交易风险控制提示，从而弱化信用违约交易风险。

3 结束语

随着金融衍生产品的进一步丰富化和全球金融协作趋势向个体经营与金融产业协同渗透方向的不断迈进，越来越多的信用违约互换定价问题逐步显现。2016年9月23日，中国版CDS——信用风险缓释工具（Credit Risk Mitigation,CRM）正式发布，这种新的信用风险缓释品种的出现能够有效地丰富市场和企业风险管理的手段，进一步促进风险分担的市场化，大力推动金融体系的效率提升、促进我国实体经济“去杠杆化”的有效实现，也标志着我国国金融领域的创新进入了一个新阶段。新的金融衍生产品对信用违约风险控制提出了更高的要求。本文针对上市公司一篮子信用违约互换定价在不同设定节点间对应的预期定价进行分解，并结合时序Copula函数进行相应的频次影响评估。当然，由于造成上市公司一篮子信用违约互换定价的因素不仅受到外部宏观条件和环境因素的影响，更受到上市公司内部信用违约互换定价机制的相互作用，单纯通过预期定价效益的分解评估，并不足以解释复杂的信用违约互换定价问题。因此，进一步探究时序Copula模型以及相关的EVT、KMV等工具对这一问题的应用，有利于更进一步细化极值分布、商业信用向金融风险的流动性过渡以及二次违约联合违约信用概率的独立判断等问题。

[1]苟红军,陈迅,花拥军.基于GARCH-EVT-COPULA模型的外汇投资组合风险度量研究[J].管理工程学报,2015,29(1).

[2]张茂军,赵雪妮.基于t-Copula的一篮子信用违约互换定价模型[J].经济数学,2014，(4).

[3]闫东玲,申文旭.信用违约互换在商业银行中的应用——基于中小企业融资难问题[J].甘肃科学学报,2016,28(2).

[4]马俊美,梁进.一篮子信用违约互换定价的偏微分方程方法[J].高校应用数学学报,2008,23(4).

[5]王倩,吴承礼.“信用违约互换”裸卖空的风险与管制[J].深圳大学学报:人文社会科学版,2016,33(3).

[6]刘向华,李林娜.基于KMV-GARCH-t-Copula模型的上市公司BDS定价研究[J].统计与决策,2015,(3).