基本概率预期下灰霾治理的最小化风险策略

王 夙

（工业和信息化部中国电子信息产业发展研究院 政策法规研究所，北京 100846）

0 引言

我国经济的快速增长在提高人们生活水平的同时，也给自然环境的承载能力带来巨大压力。随着我国逐渐步入工业化后期发展阶段，劳动密集型产品的生产处于历史转折点，此阶段工业生产对自然环境的污染表现出最为严重的现象，雾霾污染也成为影响人们生活质量提升的重要因素。如何对灰霾治理的成本和收益进行比较研究，得到灰霾治理的最小化风险策略是当前面临的重大现实问题。传统的算法因限于线性函数的设定及定量化数据的要求，无法对灰霾治理进行科学有效地测度。本文试图结合概率论和统计学的知识提出基本概率预期下灰霾治理的最小化风险策略模型，对当前的灰霾发展及治理提供较为准确的算法，并甄别出最佳治理方案。

1 灰霾治理最小风险策略的数学表达式

最小风险模型最早来源于1985年Sleator提出的竞争比分析方法，该分析方法通过计算机终端设备进行最优的算法计算，能够对所要分析的每一个因素变化所带来的最优方案变动给出一定的优化区间，在此区间内求出风险最小时方案的最优解，相对于传统的优化算法具有特殊的优势。最小风险模型的基本算式可以用以下公式表述：

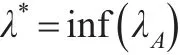
随着灰霾现象的不断发展，对人们生活质量的提升造成的消极影响越来越大，政府部门和企业都对该现象给予高度重视，灰霾的治理需要投入一定的治理费用，产生的收益则是清洁的空气和舒适的生活环境，而灰霾治理费用的投入及收益的大小伴随一定的治霾风险，因此在灰霾治理过程中一定要考虑治理风险问题。传统的算法并未考虑到治理风险的承担问题，只是探讨无风险情况下的灰霾治理问题，本文把灰霾治理的风险加入到竞争比算法中，试图构建一种比竞争比分析方法计算更为精确的模型，求出比竞争比分析结果更优的解。借用机会成本的概念对风险策略下的竞争比进行量化研究，用公式表述如下：

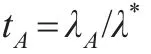
其中λA表示考虑风险的最优竞争比，λ*表示未考虑风险的最优竞争比，当该比值越大时表示该治理方案的风险也越大，该比值越小时表示该治理方案的风险越小。这就是最小风险模型的基本原理，预期是最小风险模型中的一个重要概念，由于人们认知的有限性，预期F总是不能全部覆盖所有可能的因素I，即预期F是所有影响因素I的子集：

当预期越接近于事实时，该方案的风险就会越小，即：

最小风险模型下的最优竞争比可用如下方式表述：

最小风险模型下治理收益的表达方式为：

最小风险模型不仅考虑灰霾治理的投入和收益，而且能通过公式算法求出最小风险。本文使用概率预期对上述的模型预期进行表述，假设决策者的决策集I为：

其中Fi表示决策者的预期决策，且满足以下条件：

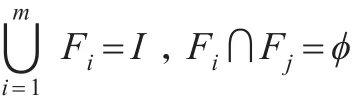
Fi决策出现的概率为Pi，且

该模型下Fi决策的最优竞争比和预期收益额表达方式分别为：

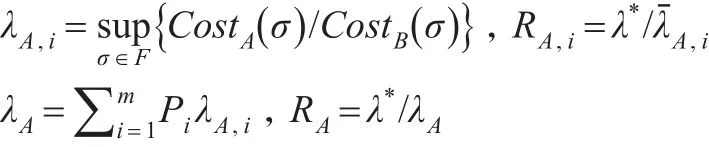
使用上述最优竞争比和预期收益公式可以设计出灰霾治理的最小风险策略：

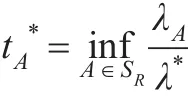
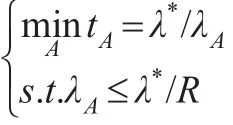
2 基本概率预期下灰霾治理的最小风险策略

假设灰霾治理的固定投入为C，变动投入为B，造成的环境污染成本为L，雾霾污染量为Z，且：

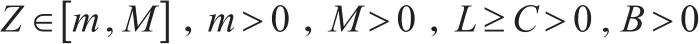
根据最小风险模型可知灰霾治理量为Q时的竞争比为：

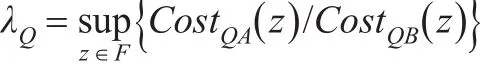
需要治理的灰霾量Q的策略集合S为：

在存在风险的情况下，灰霾治理的数量具有一定的不确定性，此时：

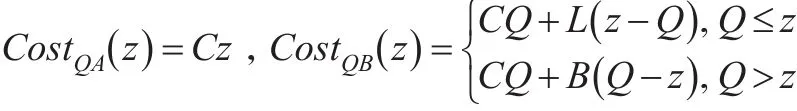
由于灰霾治理区间为[m，M]，可求出此时灰霾治理的最优竞争比为：

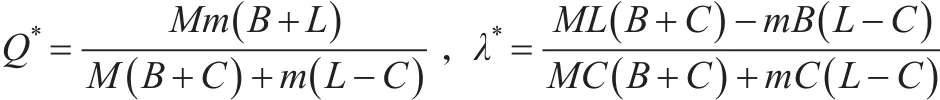
把灰霾治理区间分为两部分：[m,a]和[a,M]，则：

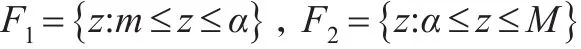
每个区间的概率设定为P1和P2，且P1+P2=1，当区间为[m,a]时灰霾治理的最优竞争比为：

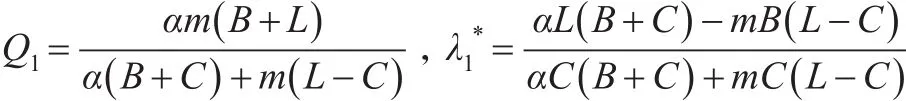
当区间为[a,M]时灰霾治理的最优竞争比为：

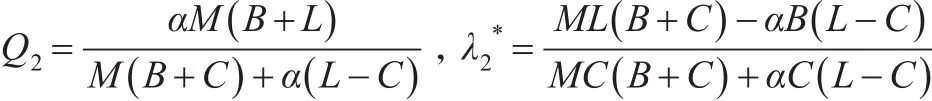
假设灰霾治理的收益为R，此时最小风险策略Q**满足以下条件：

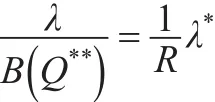
当P等于0时灰霾治理的最小风险策略Q**满足以下公式：

3 灰霾治理最小风险策略的统计学分析

为了论证本文构建的基本概率预期下灰霾治理的最小风险策略的科学性，把基本概率预期进行无限程度的细分从而得到灰霾治理的统计分布，假设概率预期的表述形式为：

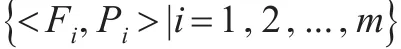
对Fi进行无限程度细分后满足以下条件：

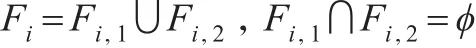
其中 Fi，1和 Fi，2的概率预期分别是 Pi,1和 Pi,2，且二者之和为Pi：

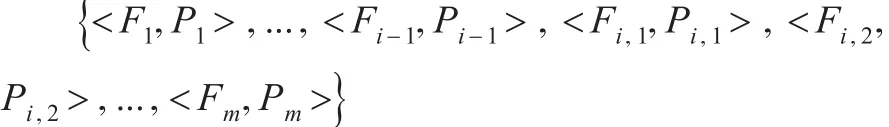
假设灰霾治理量属于一种随机分布，用X表示灰霾治理随机变量，用F（z）表示灰霾排出量的概率分布，f（z）表示灰霾排出量的概率密度函数，则灰霾治理的概率竞争比为：

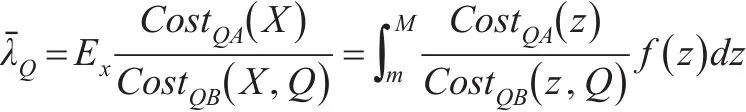
考虑风险时灰霾治理的概率竞争比为：

假设确定一个灰霾治理的预期收益R，此时灰霾治理的最小风险策略Q**的形式可以表述为：

把灰霾治理的所有可行的策略集SR表述为：

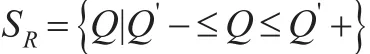
当Q≤Q*时tQ是单调递减的，当Q>Q*时tQ是单调递增的，因此灰霾治理的最小风险策略可以表述为：

当灰霾治理的预期收益R确定后，概率密度函数f（z）的形式为：

4 算例

假设灰霾治理的预期收益为R，灰霾治理的固定成本C为20个标准单位，灰霾治理的变动投入B为17个标准单位，灰霾污染的环境成本L为31个标准单位，灰霾排出量的区间范围为每天[2500，5000]个单位，且满足以下条件：

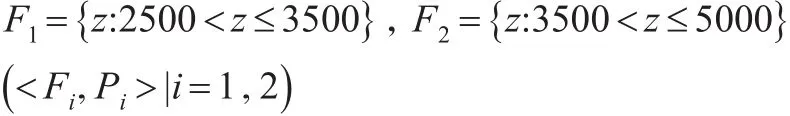
通过对F1和F2的概率进行变动来求解最小风险策略，同时对不同的概率取值本文设定不同的预期收益，算例计算结果见表1。

表1 基本概率预期下灰霆治理的最小风险策略

表1中第1列为F1预期情况下的概率P1，第2列为F2预期情况下的概率P2，第3列为灰霾治理的最大预期收益水平，第4列为灰霾治理设定的收益水平，第5列为灰霾治理的最小风险策略，第6列为灰霾治理的最小风险。当灰霾治理的收益水平预期较大时由于不能求出最优解，因此此种情况下没有最小风险策略。为了求出灰霾治理的最小化风险策略，第4列设定的灰霾治理收益均稍小于最大的预期收益。首先，当P满足以下条件时本文称为小概率：

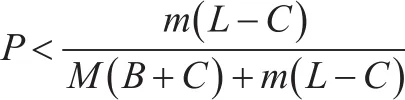
根据上式可以求出表1中P1的值为0.1～0.2时是小概率，亦即表1中的第2～5行。第2～5行的结果显示当灰霾治理的预期收益较大时也会承担较大的风险，概率为0.1时预期收益为1070，最小风险为1.57，预期收益为1060，最小风险为1.45。概率为0.2时预期收益为1040时最小风险为1.66，预期收益为1030时最小风险为1.50。因此在小概率情况下，预期收益为1060时的风险最小为1.45，此时的最小风险策略为215.66。

当P满足如下条件时表示灰霾治理的大概率：

表1中第6～14行为灰霾治理的大概率，从第6～14行的算例结果可以看出，当P1固定后，灰霾治理的最小风险策略随着预期收益设定的增加而减小，此时的灰霾治理的风险则随着预期收益的增加而变大。具体来看，当P1为0.4～0.9时属于灰霾治理的大概率情况，此时灰霾治理的设定的最大收益R为概率为0.9时的1270，此时最小风险策略为217.37，最小风险为1.39；最小风险策略Q**出现在概率为0.4时的183.76，此时最大收益为1000，最小风险为1.40；最小风险t出现在概率为0.8时的1.26，此时最大收益为1080，最小风险策略为249.10。

表1的算例结果表明当灰霾治理为小概率情况时，可以求出唯一的灰霾治理最小风险策略，而当灰霾治理为大概率情况时，灰霾治理的最小风险策略不唯一。为了检验大概率情况下的灰霾治理的最小风险策略，假设雾霾治理属于均匀分布函数，进行算例计算求解，此时参数的设定和表1中的参数设定相同，求出的最小风险策略和最小风险见表2。

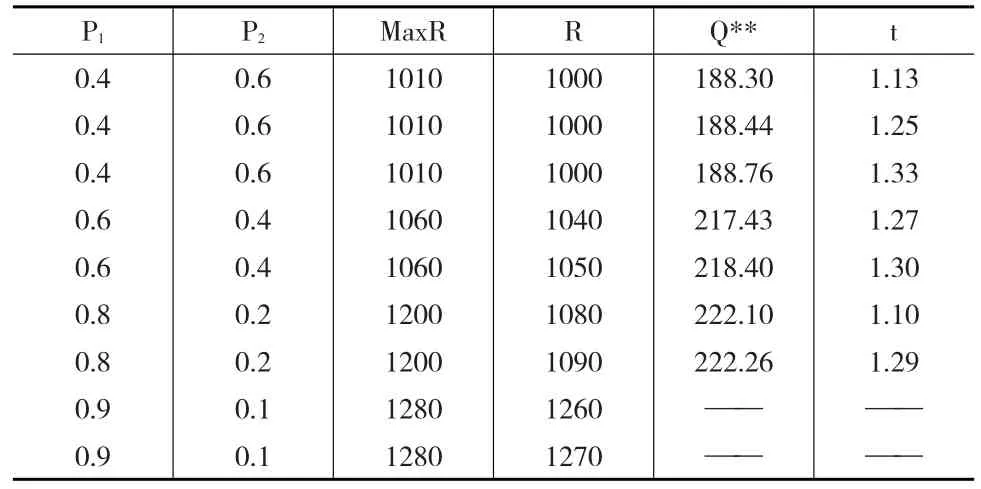
表2 均匀分布条件下的最小风险策略

从表2的算例结果可以看出，最小风险随着预期收益的增加而变大，当预期收益达到1260时出现无解情况，最小风险出现在概率为0.8时的1.10，此时的预期收益为1080，最小风险策略为222.10，虽然预期收益不是最大但和最大收益1090相差10个标准单位，出现次优解。而这个次优解正是基本概率预期模型下的其中一个解，因此可以最终确定大概率情况下的灰霾治理的最小风险策略。

5 结束语

本文在Sleator提出的竞争比分析方法的基础上进行拓展研究，构建基本概率预期下灰霾治理的最小风险策略模型，对灰霾治理的最优策略进行论证分析。认为当灰霾治理的收益水平预期较大时不能求出最优解，因此此种情况下没有最小风险策略，当灰霾治理的收益预期小于最大水平时，可以分为小概率情况和大概率情况两种类型分别求解，小概率情况下可以使用基本概率预期模型求出灰霾治理的最小风险策略，而此时大概率情况容易出现多重解，使用统计学算法可以对多重解进行甄别，最终确定大概率情况下的灰霾治理的最小风险策略。

随着我国逐渐步入工业化后期发展阶段，劳动密集型产品的生产处于历史转折点，此阶段工业生产对自然环境的污染表现出最为严重的现象，雾霾污染也成为影响人们生活质量提升的重要因素，如何对灰霾治理的投入和收益进行比较研究，求出灰霾治理的最小化风险策略是当前面临的重大现实问题。传统的测度方法因限于线性函数的设定及定量化数据的要求，无法对灰霾治理进行科学有效地测度。本文提出的基本概率预期下灰霾治理的最小化风险策略模型结合了概率论和统计学的知识，可以对当前的灰霾发展即治理提供较为准确的测度，并甄别出最佳治理方案。

[1]Hoonoum M,Zhang A M,Zhang Y M.Optimal Demand for Travel Lease of City Eco-tourism[J].Transportation Research,2014，(6).

[2]Geyrre D A.Is Employment Travel Risk Expenditure Productive?[J].Journal of Monetary Economics,2015，(23).

[3]Gienrue.Is Travel Risk Expenditure Stimulative?[J].Contemporary Pol⁃icy Issues,2015，(7).

[4]Nye S S.The Effect of Finance Risk CPI in the City Analsis of Cargo Hanling Operations[J].Physica-VerlagHD，2000，(4).

[5]Weber P.Theory of the Travel Industry Location of City[M].Chicago:The University of ChicagoPress,2007.

[6]Kiuejnr E M.The Location of Travel in Economic Activity of Inflation[M].New York:Mc Graw-Hill,2010，(4).

[7]Wardman H.Interurban Travel Demand Elasticity and Employment Risk Competition in Great Britain:Evidence From Direct Demand Models of City[J].Transportation Research,2013,5(4).

[8]孟庆春，黄伟东，戎晓霞.基于合作博弈的山东省灰霾治理收益及补偿机制研究[J].经济研究,2017,(6).

[9]毛敏娟,刘厚通,徐宏辉等.多元观测资料融合应用的灰霾天气关键成因研究[J].数量经济技术经济研究,2017，(5).

[10]张桂清,徐寅峰.概率预期下在线报童问题的最小风险策略[J].南开经济研究,2017，(7).