基于联合随机过程模型的个人账户替代率研究

梁志伟，黄健元

（河海大学a.理学院；b.公共管理学院，南京211100）

0 引言

为了应对人口老龄化的压力，我国城镇职工基本养老保险制度由现收现付制转为“统帐结合”的部分积累制，个人账户养老金成为职工退休后基本养老金的重要组成部分，保障着退休人员的生活水平，而这种保障水平主要以个人账户替代率来衡量。目前个人账户替代率取决于个人账户养老金的计发方式，而计发方式则是根据个人账户基金精算平衡原理设置的。个人账户基金精算内容主要包括基金缴费精算现值以及给付精算现值，这涉及到资金的时间价值，因此利率是重要的变量之一。

现有文献对个人账户替代率的研究主要有王海东（2013）在研究退休年龄政策对个人账户替代率的影响中，通过建立个人账户基金精算模型得出不同情况下个人账户替代率计算公式，认为提高退休年龄能够显著提高养老金替代率。宋世斌等（2006）同样地建立个人账户精算模型对个人账户政策调整前后的替代率进行了精算分析，发现调整后的替代率水平有所下降。他们的研究中都是将利率作为固定常数处理，这主要是因为我国利率长期处于管制状态，将利率作为固定常数有其合理之处。但是考虑到我国市场经济不断发展，利率市场化改革不断推进，未来的利率将实现完全市场化，此时利率将具有随机性，若仍将利率作为常数处理则会产生一定偏差，因此有必要将随机利率引入个人账户基金精算模型中。正如王茶香（2015）研究随机利率对养老金个人账户的影响时，就是将利息力积累函数作为随机变量处理，得出相同条件下随机利率比固定利率模型计算出来的养老金个人账户积累值要大，但是其并没有考察随机利率下个人账户替代率情况，而且在利息力积累函数中只加入了单一的随机过程，所以本文试图在利息力积累函数中加入不同随机过程，得出基于联合随机过程模型的个人账户替代率精算表达式。

1 个人账户养老金替代率精算模型

1.1 固定利率下个人账户基金精算模型

个人账户基金精算平衡是指：参保职工在职期间缴费在某一时刻的精算现值与退休后未来给付在这一时刻的精算现值相等。根据这一原理在计算缴费精算现值时假设职工参加工作就开始缴纳养老保险金，参加工作年龄为a岁，退休年龄为b岁。工作第1年工资为Wa，个人账户缴费率为cr，记账利率为r，x岁职工在未来k年仍活着的概率为kpx，工资年增长率为g。

则工作第1年初的缴费在参加工作时的精算现值为：

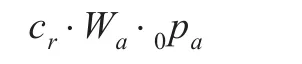
工作最后一年的缴费在参加工作时的精算现值为：

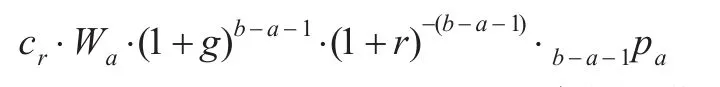
于是a岁职工在职期间缴费在参加工作时的精算现值I为：

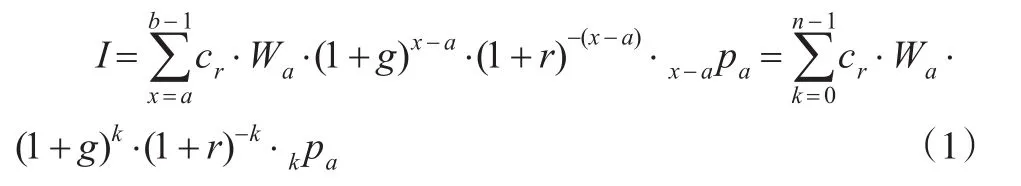
其中，n=b-a。

同时在计算给付精算现值时假设职工生存的极限年龄为ω岁，退休后每年从个人账户领取的养老金为Q，固定利率下个人账户替代率为Ti。

则退休后第1年年初养老金给付在参加工作时的精算现值为：

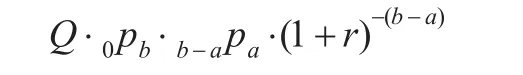
退休后第ω-b年年初养老金给付在参加工作时的精算现值为：

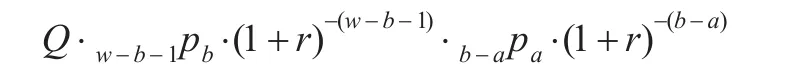
于是a岁职工退休期间养老金给付在参加工作时的精算现值E为：

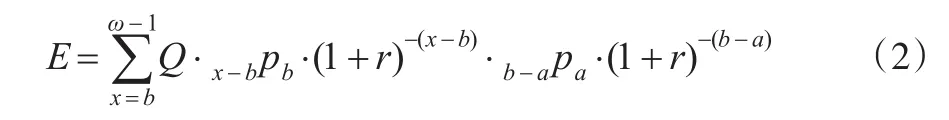
又因为Q=Ti·Wb-1，即养老金等于个人账户替代率乘以退休前一年的工资。则：

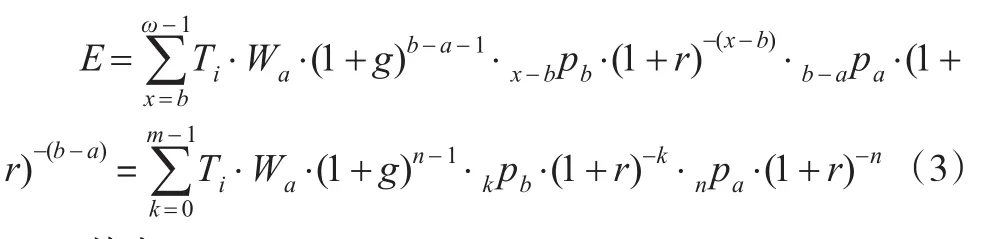
其中，m=ω-b。

当个人账户基金处于精算平衡时，即I=E，由此可得：

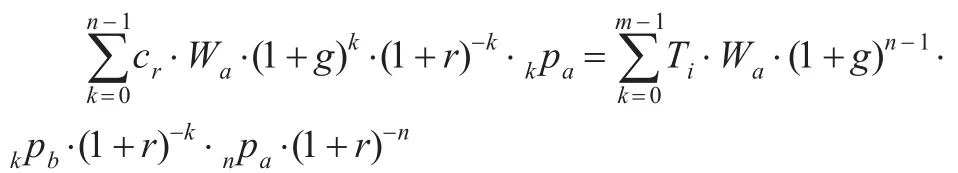
于是固定利率下个人账户替代率Ti表达式为：

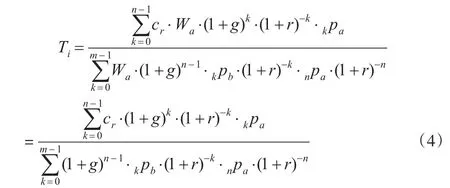
1.2 随机利率下个人账户基金精算模型

所谓随机利率，就是把利率作为随机变量来处理，将不同的随机过程引入到利息力积累函数R(t)中，由此得到随机利率下个人账户基金精算模型。由于一般金融数学文献大多以布朗运动来对随机利率进行刻画，因此本文在R(t)中引入标准Wiener过程，同时考虑到一些非预期因素对利率的影响，因此将Poisson过程也纳入其中。本文接下来给出这两种随机过程的相关结论。

引理1：设W(t)为标准的Wiener过程，a≥0为常数，则：

证明：W(t)为标准的Wiener过程，则W(t)～N(0，t)，所以：

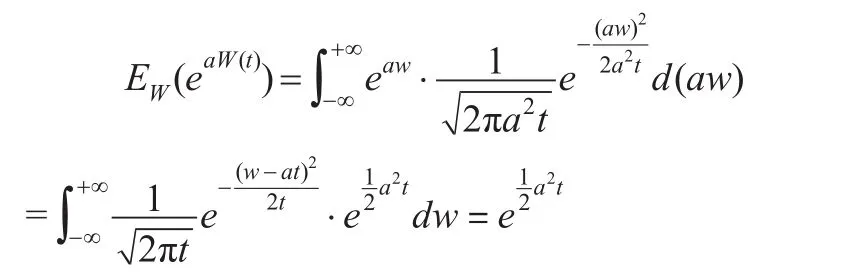
引理2：设P(t)为一个Poisson过程，且参数为λ(λ＞0)，a为常数，则：

证明：P(t)是服从参数为λ的Poisson过程，则P(t)的分布函数为：

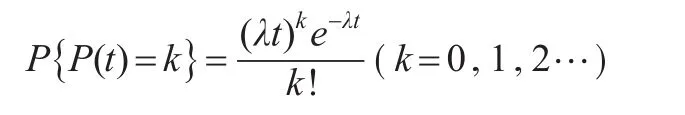
所以：

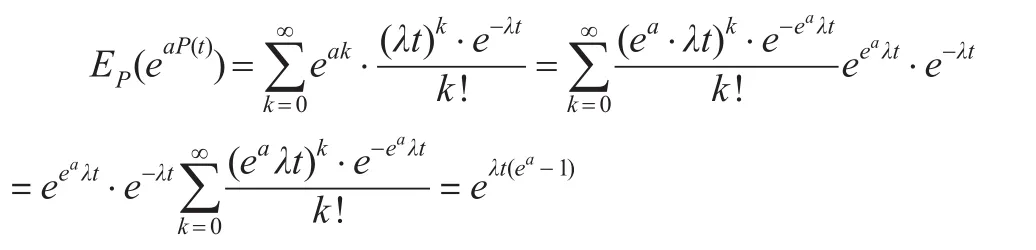
接下来建立联合标准Wiener过程和Poisson过程下个人账户基金精算模型。

设利息力积累函数为：

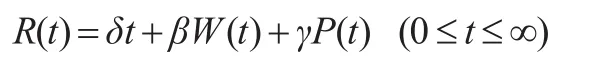
其中，W(t)为标准的Wiener过程，P(t)为Poisson过程，δ，β，γ均为常数。

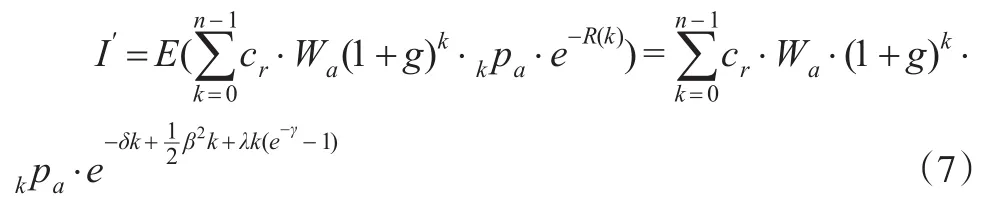
根据公式（3）可知随机利率下个人账户基金给付精算现值E′为：

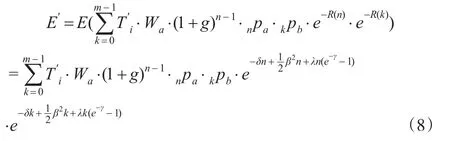
当个人账户基金处于精算平衡时，即I′=E′，由此可得：

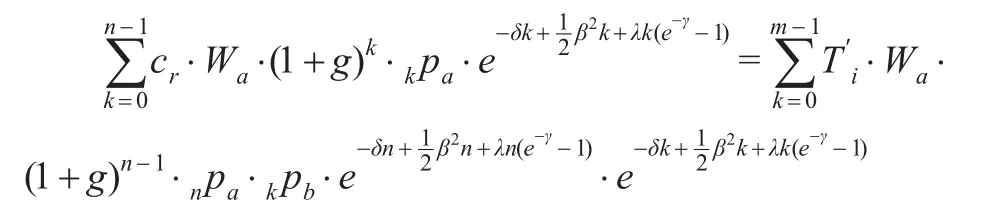
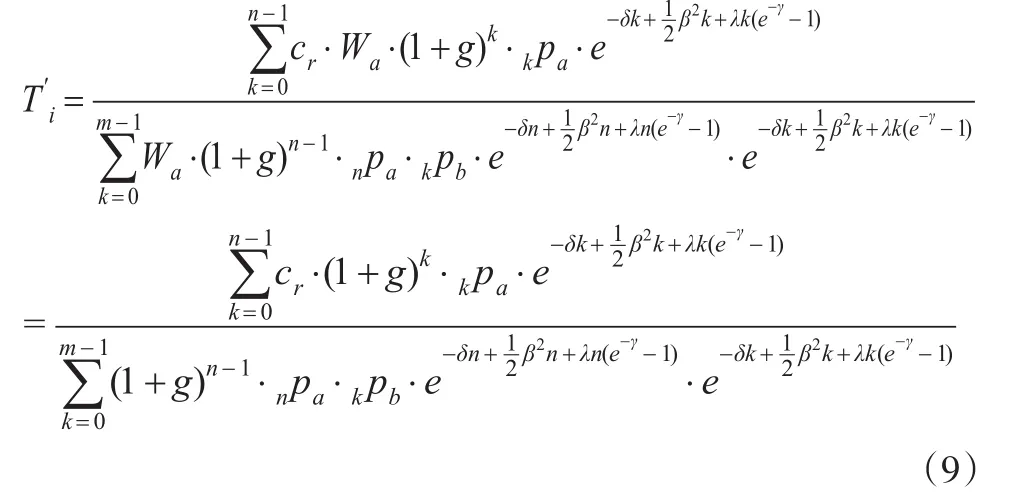
由此得到联合标准Wiener过程和Poisson过程下个人账户替代率的精算表达式。

2 实证分析

2.1 参数设定

（1）假设职工开始参加工作的年龄为20岁，为了考察不同退休年龄下个人账户替代率情况，本文将退休年龄区间设定为[50,65]。

（2）假设职工工作第1年工资设为1，且职工每年工资平均增长率为8%。

（3）人口死亡率数据来源于《中国2010年人口普查资料》中的城镇人口死亡数据，同时本文将极限年龄设定为90岁。

（4）个人账户的缴费率为8%。

（5）为了考察不同利率水平下个人账户替代率情况，本文假设固定利率分别取3%、4%和5%三种情况。

（6）利息力积累函数R(t)=δt+βW(t)+γP(t)(0≤t≤∞)中δ取值对应于固定利率下的水平，即δ取值分别为3%、4%和5%，考虑到经济环境中随机因素对利率影响强度并不是太大，因此将β和γ均设为0.1，其中Poisson过程的λ取为0.01。

2.2 不同利率处理方式下个人账户替代率情况

根据上述参数设定情况，本文首先将利率作为固定常数处理，根据公式（4）计算得出固定利率下不同退休年龄的个人账户替代率情况（见表1）。

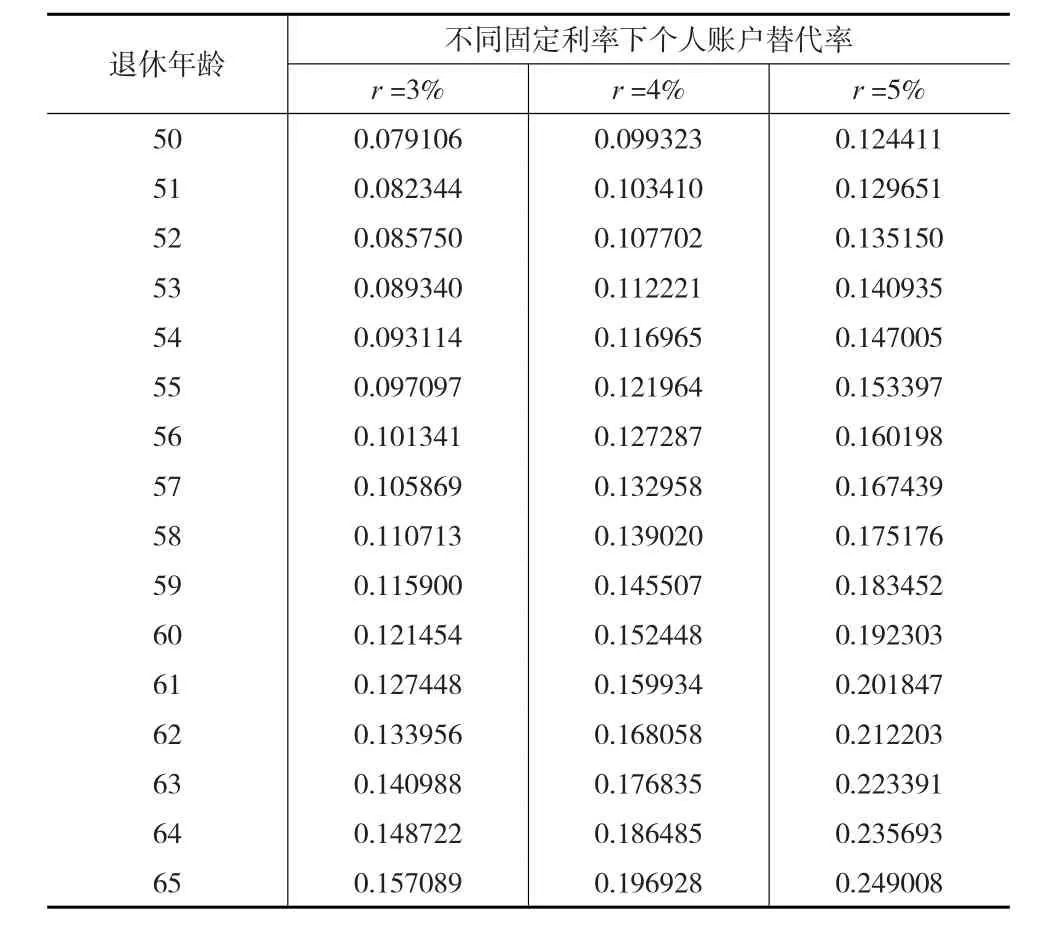
表1 固定利率下不同退休年龄个人账户替代率情况

由表1可知，当利率不变的情况下，随着退休年龄的提高，个人账户替代率水平也相应提高，以固定利率水平4%为例，50岁退休时个人账户替代率不到10%，而选择60岁退休，则替代率水平将超过15%，而到了65岁退休个人账户替代率会接近于20%，这主要是因为退休年龄越高，个人账户基金的积累时间越长，基金累积额越多，所以替代率也越高。从这方面来看个人账户的设置对延迟退休具有一定的激励作用。另一方面可以发现当退休年龄不变时，固定利率水平越高，个人账户替代率水平也越高。同样地以60岁退休为例，当利率水平分别为3%、4%和5%时，个人账户替代率水平分别达到12.15%、15.24%和19.23%。由此可见利率水平对个人账户替代率的提高效用较为明显。这是因为个人账户实行的是完全积累制，利率越高说明基金收益率越高，因此基金累积额越多，替代率就会越高。

以上是将利率作为固定常数处理时得到的个人账户替代率情况，接下来将利率作为随机变量来处理，根据公式(9)计算随机利率下不同退休年龄的个人账户替代率情况（见表2）。

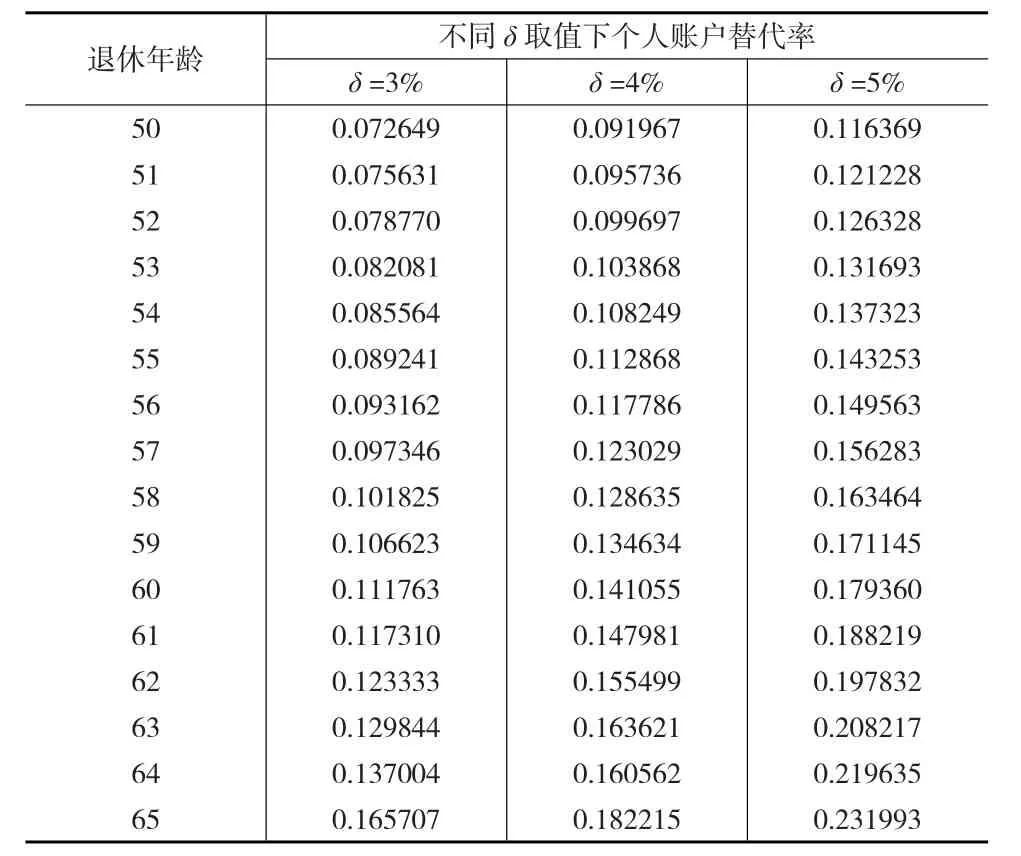
表2 随机利率下不同退休年龄个人账户替代率情况

通过表2的计算结果发现与固定利率情况相类似的是：当δ的取值相同时，退休年龄越高，个人账户替代率也越高。可见不管利率采取哪种方式进行处理，延迟退休都有助于提高替代率水平。但是从具体数值来看，以δ取值为4%，退休年龄60岁为例，固定利率下的个人账户替代率水平为15.24%，随机利率下的替代率水平为14.11%，两者之间相差一个百分点左右。由此可见随机利率下的个人账户替代率有所降低，但幅度并不大，这是因为随机利率考虑到了市场对利率的复杂影响，较低的替代率水平实际上体现了一定的利率风险，即利率变动时，较低的替代率水平更能够实现个人账户基金自身的收支平衡，有效避免个人账户出现基金缺口。同样地由表2可知，当退休年龄相同时，δ取值越大，个人账户替代率水平越高，原因与固定利率情况相同，这也说明对于完全积累制的个人账户来说，加强基金管理与运营，提高基金收益率，能够有效提高替代率水平。

2.3 随机过程参数的敏感性分析

通过表1和表2，本文分析了不同利率处理方式下个人账户替代率情况，然而本文更为关注的是联合随机过程（标准Wiener过程和Poisson过程）模型下个人账户替代率的变化情况，因此有必要对随机过程的参数进行敏感性分析，进而考察随机过程参数变动对替代率的影响程度。本文对参数β和γ分别取0.1、0.2和0.3进行不同组合，同时退休年龄选取50岁、55岁、60岁和65岁作为代表，而δ的取值则取中间水平4%，通过这样的设置便能深入分析不同退休年龄下随机过程参数变动对个人账户替代率的影响情况（见表3）。

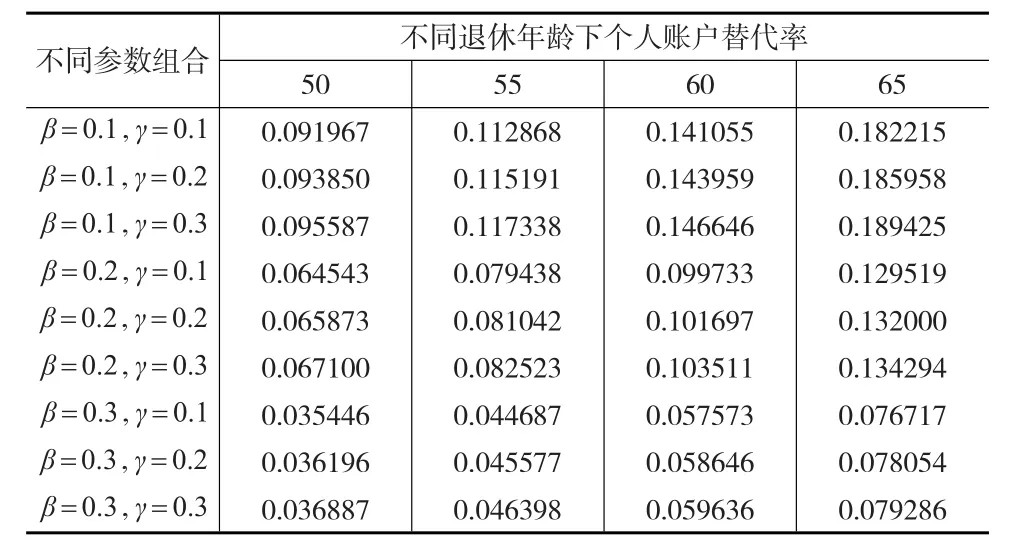
表3 随机过程参数对个人账户替代率的影响情况

根据表3的结果首先分析当退休年龄固定时标准Wiener过程参数β的变动对个人账户替代率的影响情况，以γ取0.2，退休年龄60岁为例，当β取值分别为0.1、0.2和0.3时，个人账户替代率分别为14.40%、10.17%和5.86%。可见参数β值越大时，个人账户替代率越低，此处β每增加0.1，替代率水平降低4%左右。同样地可以分析Poisson过程参数γ的变动对个人账户替代率的影响情况，以β取0.2，退休年龄60岁为例，当γ取值分别为0.1、0.2和0.3时，个人账户替代率分别为9.97%、10.17%和10.35%。可见与参数β不同的是参数γ取值越大时，个人账户替代率水平越高，但是提高幅度不大，此处γ每增加0.1，替代率水平提高约0.2%。由此可见个人账户替代率对参数β的敏感性更强，这是因为Poisson过程体现了实际利率变化过程中的一些非正常的利率干扰因素，但从长期影响来看，这样的干扰因素对利率的影响是比较小的。

通过对不同退休年龄下个人账户替代率变动情况的考察可以发现：退休年龄越高时，随机过程参数变化对个人账户替代率的影响越大。由于参数γ对替代率的影响并不大，此时主要分析参数β的变化对替代率的影响，以退休年龄50岁和65岁为例，当退休年龄为50岁时，β每增加0.1，替代率降低3%左右，而退休年龄为65岁时，β每增加0.1，替代率降低5%左右。这主要是因为退休年龄越高，个人账户基金积累的时间越长，市场的随机因素对利率的影响也更加明显，因此会出现上述情况。综上分析可知当利率处于较强随机干扰状态（参数β较大）时，个人账户替代率水平明显下降，对于基金积累时间较长情况下更是如此，因此稳定市场利率水平对于提高个人账户替代率水平而言显得尤为重要。

3 结论

（1）本文首先根据传统精算理论构建了固定利率下个人账户基金精算模型，但考虑到未来利率市场化的实现，因此有必要考虑利率的随机性，所以本文将利率作为随机变量处理，在利息力积累函数中加入标准Wiener过程和Poisson过程构建随机利率下个人账户基金精算模型，并且根据不同利率处理方式下的精算模型得出相应的个人账户替代率的精算表达式。

（2）通过个人账户替代率精算表达式中的相关参数进行设定，实证分析了不同利率处理方式以及不同退休年龄下个人账户替代率情况。结果发现：当利率水平不变时，退休年龄越高，替代率水平越高，例如退休年龄从50岁提高到60岁，替代率水平将提高5%；当退休年龄固定时，利率水平越高，替代率水平越高，例如利率从4%提高到5%，替代率水平将提高4%。其次，当其他条件一致时，随机利率下的替代率水平低于固定利率下一个百分点左右。最后对随机过程参数进行敏感性分析发现：标准Wiener过程参数β取值越大，替代率越低；而Poisson过程参数γ取值越大，替代率越高。但是个人账户替代率对参数β的敏感性更强，β每增加0.1，替代率水平降低约4%，而γ每增加0.1，替代率水平提高约0.2%，并且当退休年龄越高时，参数β的变化对替代率水平的影响更大。因此延迟退休年龄、加强基金管理与运营以提高基金收益率、稳定市场利率水平等政策能够有效提高个人账户替代率水平。

（3）本文基于联合随机过程模型所得出的个人账户替代率水平，考虑了未来利率的随机性，可以为未来个人账户基金管理以及给付提供一定的参考，比如可以调整不同退休年龄下个人账户养老金的计发月数，使得个人账户替代率达到基金精算平衡下的合理水平。但是由于影响利率的因素过于复杂，本文只考虑两种随机过程，这是本文的局限所在，同时也是本文进一步研究的方向。

[1] 王海东.我国退休年龄政策及其对个人账户替代率的影响研究[J].保险研究，2013,(5).

[2] 宋世斌，冯羽，彭俊.养老保险个人账户调整的精算分析[J].统计与决策，2006,(18).

[3] 王茶香.随机利率对养老金个人账户的影响分析[J].上饶师范学院学报，2015,(6).

[4] 高建伟，丁克诠.社会养老保险中个人账户养老金给付标准精算模型及模拟分析[J].南方金融，2005,(3).

[5] 邱菀华，高建伟.个人账户中养老金给付精算模型及其应用[J].北京航空航天大学学报:社会科学版，2002,(3).

[6] 王晓军.社会保险精算原理与实务[M].北京：中国人民大学出版社，2010.

[7] 张思锋.社会保障精算理论与应用[M].北京：人民出版社，2006.