基于累积前景理论的属性关联犹豫模糊TOPSIS方法
2018-03-21阙翠平王应明蓝以信
阙翠平,王应明,蓝以信
(福州大学决策科学研究所,福州350116)
0 引言
自Tversky等[1]于1978年提出前景理论后,一些基于有限理性的行为决策理论相继被提出。如后悔理论[2],失望理论[3],累积前景理论[4]和第3代前景理论[5]等。其中累积前景理论通过模型函数和参数调整来准确描绘决策者偏好风险(面对收益时)和厌恶风险(面临损失时)的心理特征,更符合在不确定环境下决策者所做出有限理性的决策行为。目前,已有学者将累积前景理论运用于决策分析,如刘思峰等[6]运用累积前景理论解决动态风险灰靶决策问题;樊治平等[7]运用累积前景理论解决具有决策者期望的混合型多属性决策问题;Li[8]提出一种基于累积前景理论和D-S理论的决策分析方法。但现有的研究并未对累积前景理论与犹豫模糊集相结合的多属性决策问题进行探讨。
本文就属性值为犹豫模糊集且属性间存在关联的风险型决策问题为背景,结合决策者的主观风险态度,提出一种基于累积前景理论的属性关联犹豫模糊TOPSIS风险型多属性决策分析方法。首先,对属性值进行规范化处理,确定正、负理想解为决策参考点,定义了犹豫模糊数的前景价值函数,同时结合累积决策权重函数计算针对犹豫模糊信息的累积前景矩阵。然后,通过2可加模糊测度对属性集的权重建模,应用Choquet积分的思想,对经典逼近理想解法进行改进,给出属性关联下方案与理想解的距离公式,并以此计算各个方案的改进型关联度。最后,对备选方案进行优劣排序,并结合例子分析证明该方法的可行性。
1 基础理论
1.1 模糊测度和Choquet积分
定义1[9]:设P(X)为X={x1,x2,…,xn}的幂集,μ为定义在P(X)上的集函数,μ:P(X)→[0,1],若μ满足以下性质:
(1)μ(ϕ)=0,μ(X)=1;
(2)若A⊆B⊆X,则μ(A)≤μ(B)≤μ(X);
则称μ为定义在P(X)上的模糊测度。
利用模糊测度对单个属性的全局重要度建模,不仅要考虑单个属性的测度值,还需考虑属性集测度值。即:假设X为某个多属性决策问题的指标集,则对于任意A,B∈P(X)且A∩B=ϕ,μ(A)和μ(B)可以解释为属性集A,B的权重或者重要程度。若μ(A)+μ(B)<μ(A∪B),则说明属性(集)A,B间存在补充关系;若μ(A)+μ(B)>μ(A∪B),则说明属性集A,B间存在冗余关系;若μ(A)+μ(B)=μ(A∪B),则说明属性集A,B相互独立。
定义2[10]:设μ为定义在P(X)上的模糊测度,离散Choquet积分定义为f:A→R+关于μ的映射:
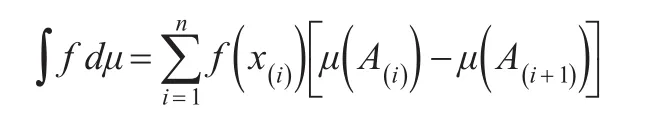
1.2 犹豫模糊集的基本知识
定义3[11]:设X是给定的论域,称|x∈X}为X上的犹豫模糊集,其中hH(x)是由区间[0,1]上几个不同的数构成的集合,表示x属于集合H的若干种可能的隶属度。)为一个犹豫模糊数,犹豫模糊数h的补为hc=H{1-γ1,1-γ2,…,1-γl},其中l表示犹豫模糊数h中元素个数。
定义4[12,13]:对任一犹豫模糊数h=H{γ1,γ2,…,γl},其得分函数s(h)和方差函数v(h)分别定义为:
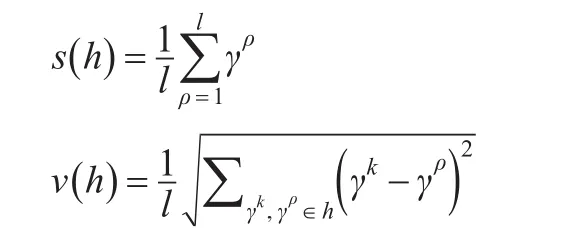
在方差函数和得分函的基础上,犹豫模糊数的排序规则为:对于任意两个犹豫模糊数h1和h2,s(h1)和s(h2)分别是犹豫模糊数h1和h2的得分值,v(h1)和v(h2)分别是犹豫模糊数h1和h2的方差,则:
(1)若s(h1)<s(h2),则h1≺h2
(2)若s(h1)>s(h2),则h1≻h2
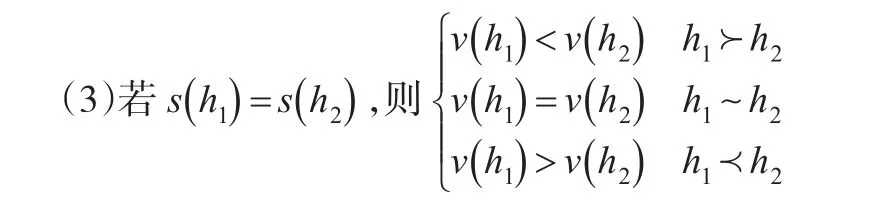
定义5[13]:对于任意的三个犹豫模糊元h、h1和h2,它们的基本运算法则如下:(其中θ是一个常数)
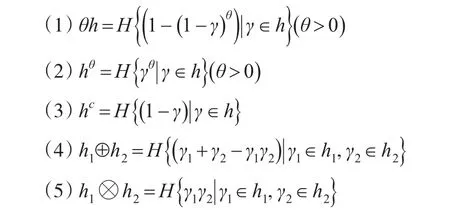
定义6[14]:设犹豫模糊数假设其中的元素按增序排列且具有相同个数,即l1=l2=l。距离测度用犹豫模糊欧氏距离测度表示(其中分别为犹豫模糊数h中第ρ小的值),即:
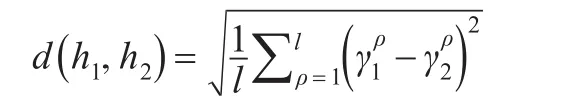
1.3 累积前景理论
累积前景理论在“有限理性”的基础上,体现决策者的主观风险偏好。累积前景值V(f)主要由两部分组成,即价值函数υ和决策权重函数π。
Tversky等提出用幂函数替代价值函数υ(Δx),体现了决策者在面临收益时更倾向于风险规避以及面临损失时更倾向于风险追求的特性,即:
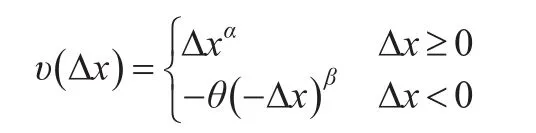
其中,Δx为x偏离某一参考点x0的大小,Δx≥0,表示获益;Δx<0,表示获弊。α,β体现了决策者对利、弊的敏感性程度。θ表示决策者对损失和收益敏感度比较来说,决策者更敏感于损失。且α,β,θ的取值范围分别为α>0,β<1,θ>1。
在多属性决策过程中,若属性值表示为犹豫模糊数,则通过利用犹豫模糊欧氏距离测度衡量各个方案偏离决策参考点的大小,定义犹豫模糊环境下的价值函数,如下所示:
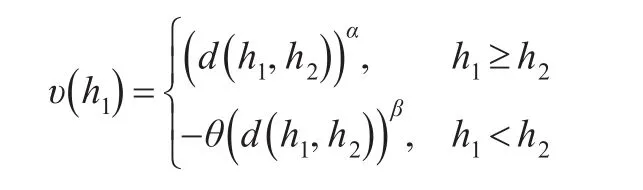
累积前景理论中的决策权重函数这一概念,体现了累积前景理论相比于前景理论的优势所在,就是不再依靠单个概率而是通过累积概率进行决策权重计算。即:根据Δx的大小将前景f表示为有序序列,使得Δx(1)≤Δx(2)≤…≤Δx(k)≤Δx(k+1)≤…≤Δx(n),收益和损失的决策权重函数表达式为:
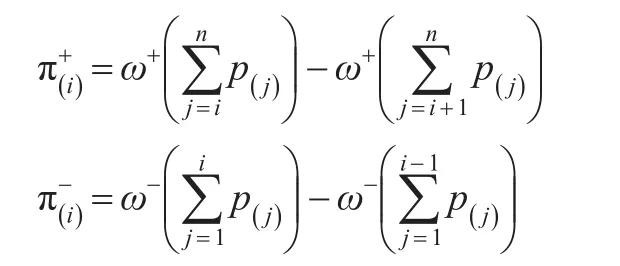
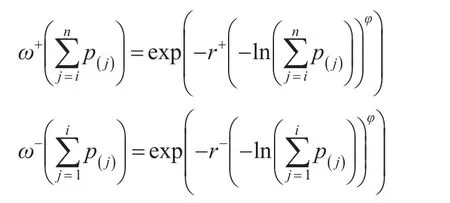
2 属性关联下犹豫模糊TOPSIS决策模型的构建
2.1 问题描述
例如一个犹豫模糊风险多属性决策问题包括m个备选方案和n个评价属性。令X={x2,…,xm}(i=1,2,…,m)表示方案集,C={c1,c2,…,cn}(j=1,2,…,n)表示属性集,且属性集不再是加性独立,而可能存在着某种关系。对于每个属性Cj有tj种可能的状态{s2,…,stj},属性cj在自然状态sk下出现的可能性为pjk。基于属性cj和自然状态sk,决策方案xi的属性值为犹豫模糊数hijk,其中hijk表现为犹豫模糊数形式,即:hijk=H{,…,,lijk表示hijk中元素个数。
2.2 犹豫模糊环境下累积前景值的计算
随着社会的发展,由于受到日益复杂化的决策问题和决策者自身的思维模式局限性的影响,决策者往往难以表达其偏好信息。同时,决策者做决策时,一般根据自身的风险偏好进行裁决。因此,本文针对风险型决策问题,提出一种犹豫模糊环境下累积前景值的计算方法,旨在解决上述问题,具体步骤如下所示:
步骤1:构造样本数据的标准化犹豫模糊决策矩阵M。
将犹豫模糊数内的各个元素按照增序方式进行排列,然后采用Xu和Xia[16]的拓展方法扩展元素个数较少的犹豫模糊数,使其具有相同的元素个数,即lijk=l。
步骤2:对标准化犹豫模糊决策矩阵M进行归一化处理。
在风险型多属性决策问题中,评价属性主要分为两大类,即效益型和成本型。为了排除不同变量对决策结果的影响,将成本型属性通过犹豫模糊数规范化方法[17]转化为效益型属性,得到归一化犹豫模糊决策矩阵,即:对效益型属性有=hijk;对成本型属性有=(),且
步骤3:决策参考点的选取。
在累积前景理论中,决策者主要根据参考点来判别各个方案的收、失情况。因此,正确选择参考点对决策结果起到至关重要的作用。本文以正负理想解作为决策过程中的参考点。
设X+为正理想解,X-为负理想解,则在属性cj和状态sk下可得:
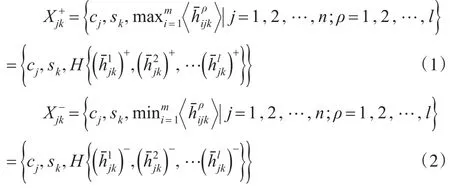
步骤4:确定方案在各状态下属性的收益、损失矩阵。
用犹豫模糊欧氏距离计算方案xi在属性cj下与决策参考点的距离。令D(xi,)和D(xi,)分别表示方案xi在属性cj下与正理想解X+和负理想解X-之间的距离集,即:
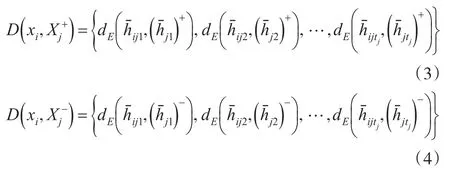
通过累积前景理论中价值函数概念以及行为经济学可以得到如下:若采用正理想解为参考点,各方案基于正理想解是损失的;反之,采用负理想解为参考点,则是获益的,即:
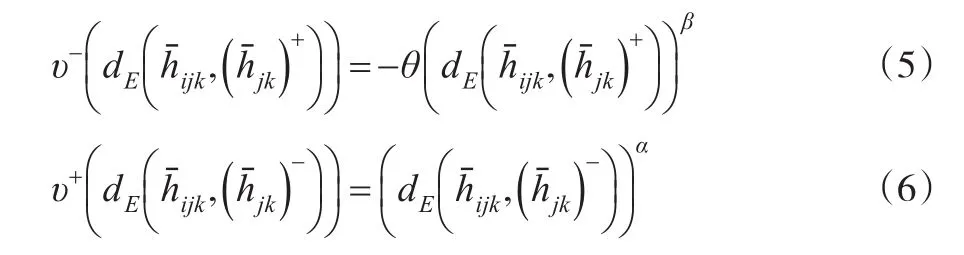
其中α=β=0.88,-0.48112[5]。
步骤5:计算各方案在各个属性下的累积前景值。
由累积前景理论可知,为计算方案xi在属性cj下的累积前景值,需根据小分别将方案xi在属性cj下的前景f表示为有序序列,使得:
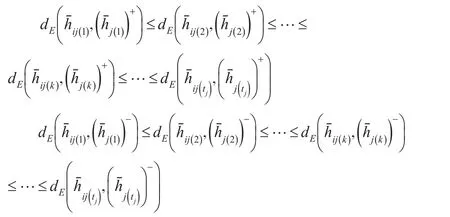
若以正、负理想解为决策参考点,得到方案xi在属性cj下的正累积前景值和负累积前景值,则有方案xi在属性cj下的累积前景值为两者之和,即:
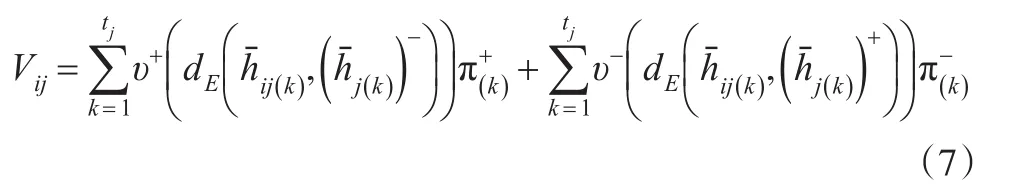
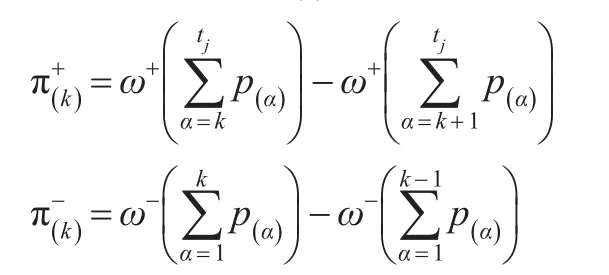
且ω+和ω-函数如下:
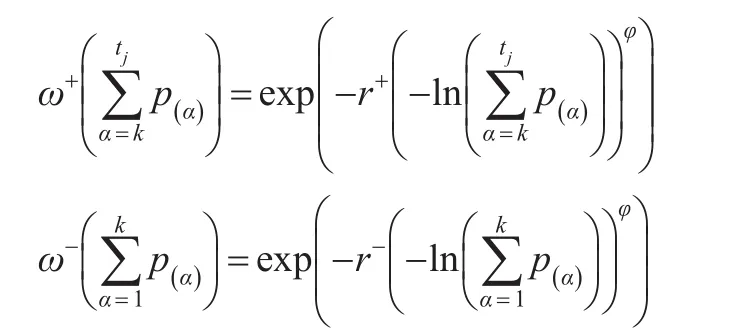
其中r+,r-,φ分别取值为r+=r-=0.8,φ=1.0[18]。
2.3 属性关联下基于累积前景理论的TOPSIS排序方法
在现实风险多属性决策中,不同属性之间总是存在着某种相互作用或关系[19]。基于此,本文在2可加模糊测度和逼近理想点法的基础上,提出一种属性关联下基于累积前景理论的TOPSIS风险决策方法,如下所示:
步骤1:依据累积前景矩阵V,确定正理想解和负理想解。设V+为正理想解,V-为负理想解,则有:

步骤2:通过2可加模糊测度对属性集的权重建模,应用Choquet积分的思想对经典逼近理想解法中计算方案到正、负理想解的距离公式进行改进。
已知专家给定属性的Shapley值和交互作用指标,对属性集权重建模。即:对属性集合C={c2,…,cn},设μ是定义在X上的2可加模糊测度,则∀A⊂X,有:然后应用Choquet积分的思想对计算方案xi到正理想解V+和负理想解V-的距离公式进行改进,表示为:
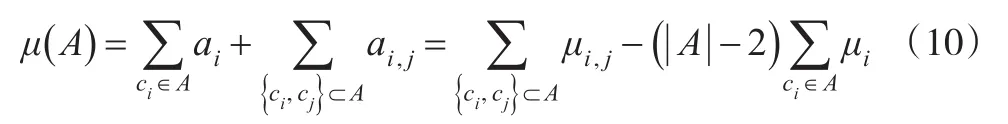
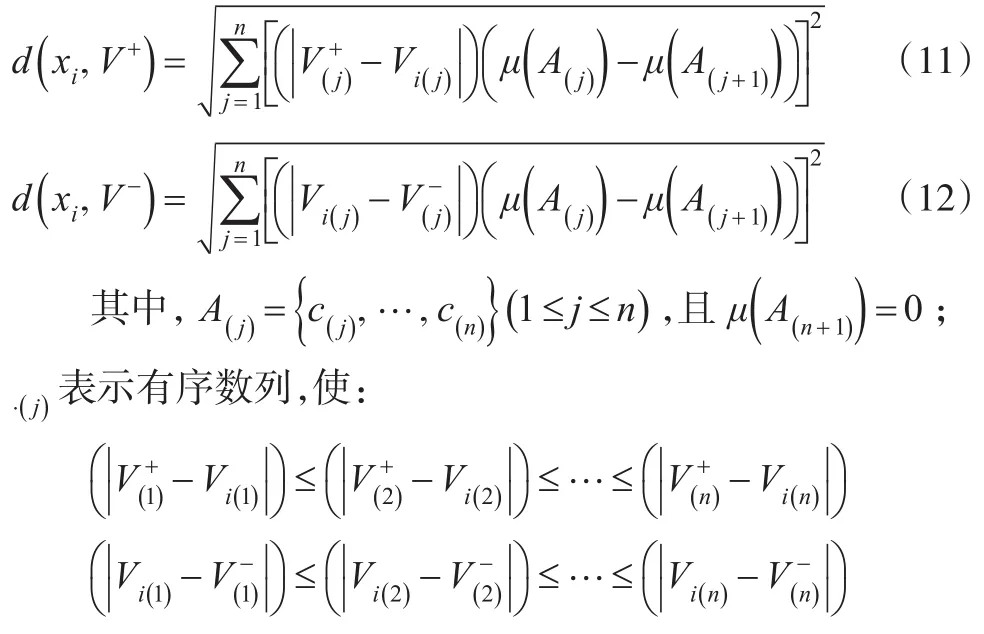
步骤3:计算各方案的改进型关联度,并对方案排序。
基于经典逼近理想点法,可得到方案xi与正、负理想解的关联度为:
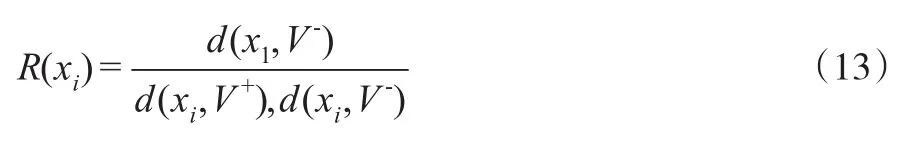
然而,学者Hadi-Vencheh和Mirjaberi[20]指出由于决策问题的复杂性以及人类自身认知的局限性,在一些现实风险型多属性决策问题中,经典逼近理想解法的相对贴近度最大的方案可能并不满足与正理想解最近、与负理想解最远。因此,基于这个思想,对于犹豫模糊环境下基于累积前景理论的TOPSIS方法,给出一种改进型关联度:
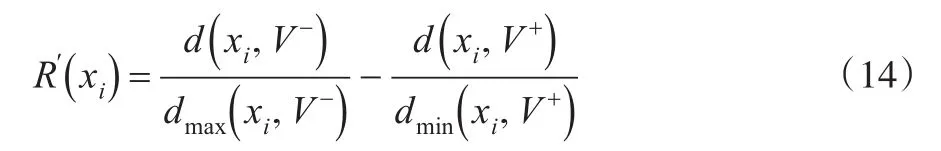
3 算例分析
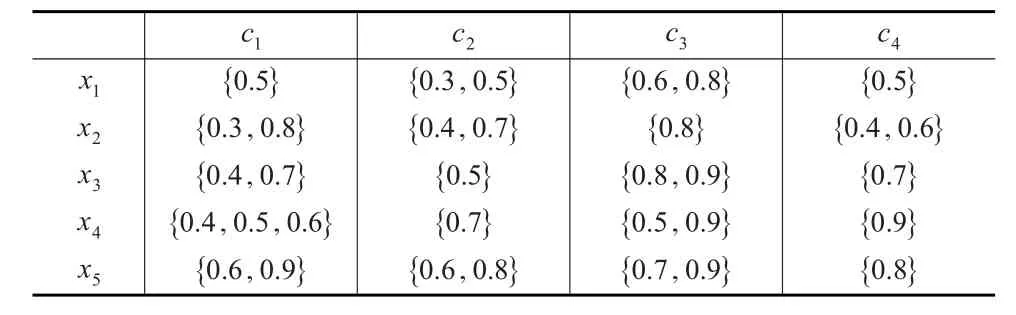
表1 s1性能决策矩阵
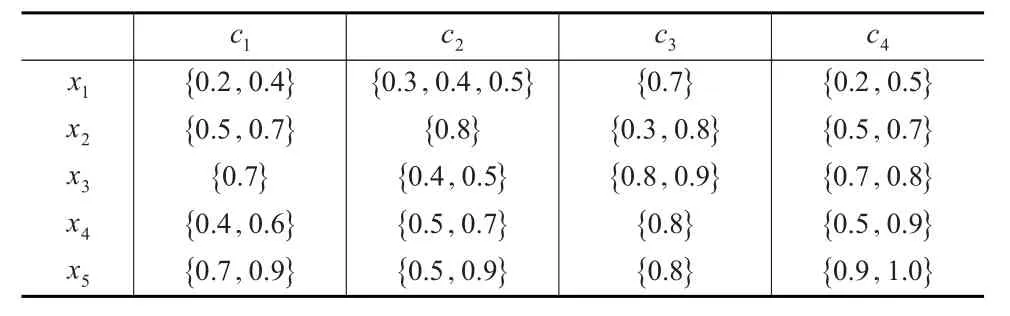
表2 s2性能决策矩阵
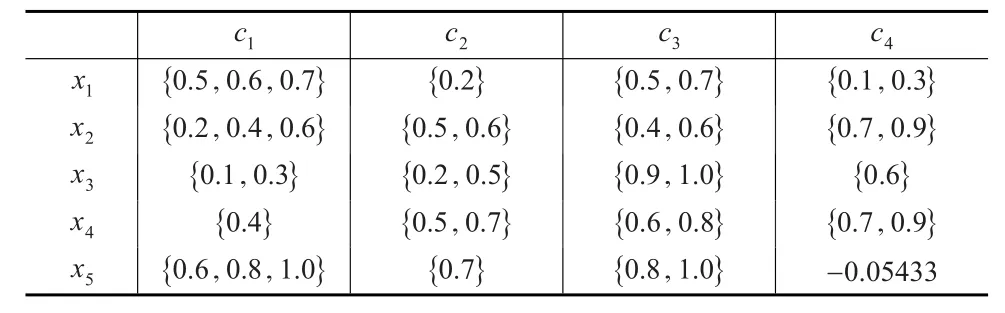
表3 s3性能决策矩阵
其中,矩阵中的元素H{0.5,0.6,0.7}表示决策组织在评价S3性能状态下方案x1满足属性c1的程度时,评估值可能是0.5或0.6或0.7,其他的数据具有类似的意义。
为了正确测度犹豫模糊数之间的欧氏距离,对样本数据进行标准化和归一化处理。不失一般性,如果决策者是风险规避型,可以通过反复增加具有较少的元素的犹豫模糊数中的最小元素,使犹豫模糊数内的所有元素具有相同的个数。
(1)根据上文中犹豫模糊环境下累积前景值的计算方法,在决策过程中以正、负理想解作为决策参考点,确定方案在各状态下属性的收益、损失矩阵,计算各方案在各个属性下的累计前景值,如表4所示。
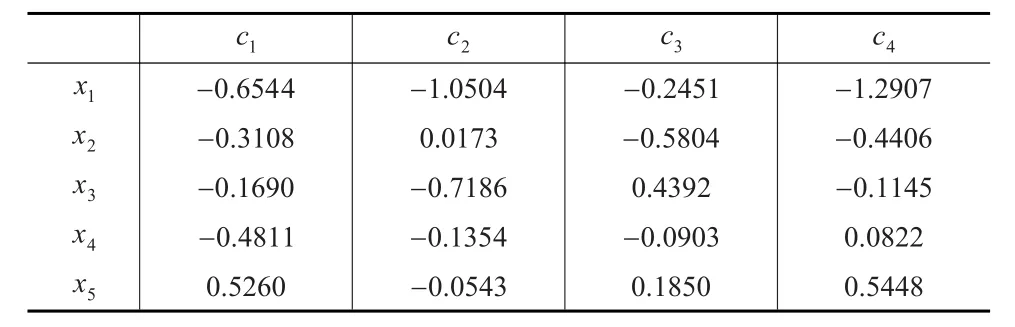
表4 累积前景矩阵V
(2)已知专家给定属性的Shapley值和交互作用指标,其中Shapley={0.18,0.25,0.36,0.21},交互作用指标为I12=-0.08,I23=-0.125,I24=-0.1,I13=I14=I34=0。根据式(10)对属性集权重建模,得到属性集所有子集的2可加模糊测度如表5所示。
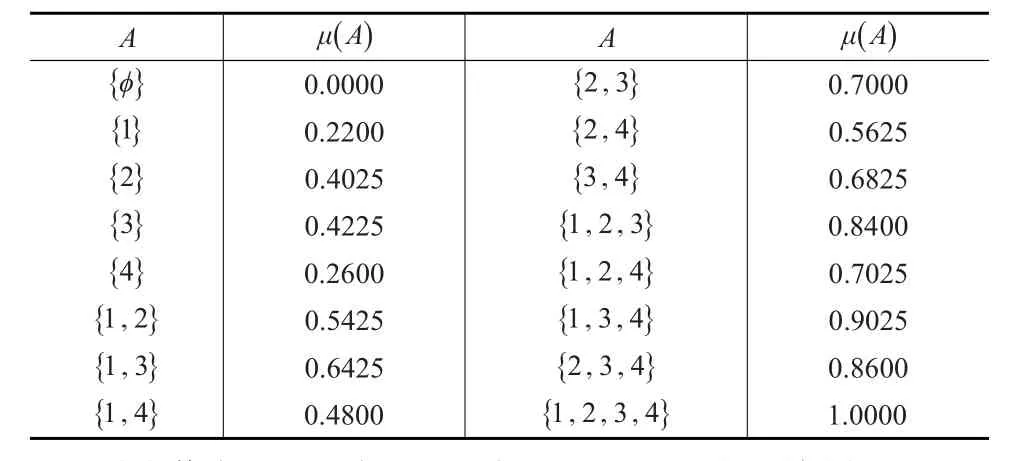
表5 属性集所有子集的2可加模糊测度值
(3)依据上文中属性关联下基于累积前景理论的TOPSIS排序方法,分别计算方案xi到正理想解V+和负理想解V-的距离,从而得到各方案的改进型关联度:
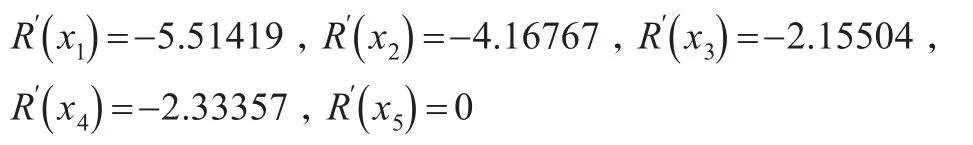
确定各方案的优劣排序为x5≻x3≻x4≻x2≻x1。因此,x5为该风险投资企业的最优选择。
为说明本文提出的方法的有效性,首先,考虑决策者的主观风险偏好和属性间的关联性,运用式(13)计算各备选方案的经典关联度。接着,只考虑决策者在决策过程中的主观风险偏好,而不考虑属性间的关联性,使用文献[21]中的方法,通过将犹豫模糊决策矩阵转化为得分矩阵,并在此基础上计算备选方案的综合前景值;再者,同时不考虑决策者的主观风险偏好和属性间的关联性,根据文献[22]的方法,设属性的权重值W={w1,w2,w3,w4}={0.18,0.25,0.36,0.21},计算备选方案的相对贴近度。以上两种方法得到的结果同本文方法得到经典关联度和改进型关联度的比较如表6所示。
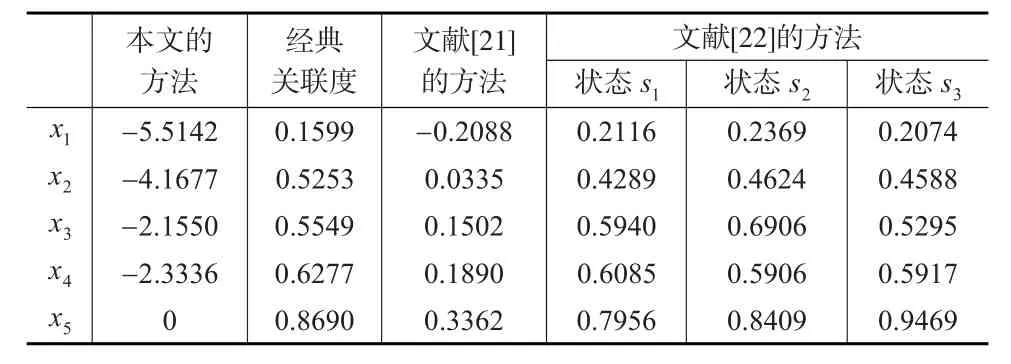
表6 不同决策方法的结果比较
由以上不同决策方法的比较研究中发现:利用基于经典关联度的决策分析方法得到的方案排序与正文方法得到的排序存在差异,可以看出犹豫模糊环境下运用改进型关联度对方案排序有一定的影响。文献[21]的方法通过计算备选方案的综合前景值进行排序,与本文方法排序不完全一致,原因在与文献[21]的方法没有考虑各属性间存在的关联性。文献[22]的方法只能针对不同风险状态得出相应的结论,且决策结果各不相同,难以为实际决策提供支撑。且其假设决策者对损失和收益持有相同的风险偏好以及属性间完全相互独立,与实际不符。
从数据中可知,在各性能状态下方案x4的c2属性值都优于方案x3的属性值,c1,c3,c4属性下方案x4与方案x3的属性值差别不大。因此,本文的方法综合考虑三种状态,同时将决策者的主观风险态度和属性的关联性引入决策中,得到x5≻x3≻x4≻x2≻x1的排序结果更加符合实际决策情形。
4 结论
本文针对属性间存在关联的犹豫模糊风险型决策问题,给出一种基于累积前景理论和改进型逼近理想解法的决策方法。依据累积前景理论,将决策者的“有限理性”引入到犹豫模糊多属性决策问题中,提出一种犹豫模糊风险环境下累积前景值的计算方法。并在此基础上,结合2可加模糊测度的概念,通过计算各方案的改进型关联度得到方案的排序结果。
[1] Tversky A,Kahneman D.Prospect Theory:An Analysis of Decision Under Risk[J].Econometrica Journal of the Econometric Society,1979.
[2] Bleichrodt H,Wakker P P.Regret Theory:A Bold Alternative to the Alternatives[J].The Economic Journal,2015,125(583).
[3] Bell D E.Disappointment in Decision Making Under Uncertainty[J].Operations research,1985,33(1).
[4] Tversky A,Kahneman D.Advances in Prospect Theory Cumulative Representation of Uncertainty[J].Journal of Risk and Uncertainty,1992,5(4).
[5] Schmidt U,Starmer C,Sugden R.Third-generation Prospect Theory[J].Journal of Risk and Uncertainty,2008,36(3).
[6] 闫书丽,刘思峰,方志耕等.基于累积前景理论的动态风险灰靶决策方法[J].控制与决策,2013,28(11).
[7] 樊治平,陈发动,张晓.基于累积前景理论的混合型多属性决策方法[J].系统工程学报,2012,27(3).
[8] Li X,Wang F,Chen X.Trapezoidal Intuitionistic Fuzzy Multiattribute Decision Making Method Based on Cumulative Prospect Theory and Dempster-Shafer Theory[J].Journal of Applied Mathematics,2014.
[9] Xu Z.Choquet Integrals of Weighted Intuitionistic Fuzzy Information[J].Information Sciences,2010,180(5).
[10] Murofushi T,Sugeno M.An Interpretation of Fuzzy Measures and the Choquet Integral as an Integral With Respect to a Fuzzy Measure[J].Fuzzy Sets and Systems,1989,29(2).
[11] Torra V.Hesitant Fuzzy Sets[J].International Journal of Intelligent Systems,2010,25(6).
[12] Xia M,Xu Z.Hesitant Fuzzy Information Aggregation in Decision Making[J].International Journal of Approximate Reasoning,2011,52(3).
[13] Liao H,Xu Z.A VIKOR-based Method for Hesitant Fuzzy Multi-cri⁃teria Decision Making[J].Fuzzy Optimization and Decision Making,2013,12(4).
[14] Xu Z,Xia M.On Distance and Correlation Measures of Hesitant Fuzzy Information[J].International Journal of Intelligent Systems,2011,26(5).
[15] Prelec D.The Probability Weighting Function[J].Econometrica,1998.
[16]Xu Z,Xia M.Distance and Similarity Measures for Hesitant Fuzzy Sets[J].Information Sciences,2011,181(11).
[17] Zhu B,Xu Z S.Hesitant Fuzzy Bonferroni Means for Multi-criteria Decision Making[J].Journal of the Operational Research Society,2013,64(12).
[18] Goda K,Hong H P.Application of Cumulative Prospect Theory Im⁃plied Seismic Design Preference[J].Structural Safety,2008,30(6)
[19] Sugeno M.Theory of Fuzzy Integral and Its Applications[D].Tokyo Tokyo Institute of Technology,1974.
[20] Hadi-Vencheh A,Mirjaberi M.Fuzzy Inferior Ratio Method For Multiple Attribute Decision Making Problems[J].Information Scienc⁃es,2014,(277).
[21] 马庆功.基于前景理论的犹豫模糊多属性群决策方法[J].计算机工程与应用,2015,51(24).
[22] Xu Z,Zhang X.Hesitant Fuzzy Multi-attribute Decision Making Based on TOPSIS with Incomplete Weight Information[J].Knowl⁃edge-Based Systems,2013,(52).
