均方误差意义下预检验两参数估计的优良性

常新锋

（江苏大学 财经学院，江苏 镇江 212013）

1 问题的提出

考虑线性模型：

其中y是n×1的响应向量，X是n×p的列满秩设计矩阵，β是p×1的未知参数向量，ε是n×1服从正态分布的随机误差向量，ε的期望为E(ε)=0，方差为E(εε′)=σ2I，σ2＞0，I是n×n的单位矩阵。

模型（1）中参数向量β带有的附加信息为以下等式约束：

其中r为q×1的随机向量，R为q×p的行满秩矩阵，且q＜p。

模型（1）中β的最小二乘估计和σ2的无偏估计分别为：

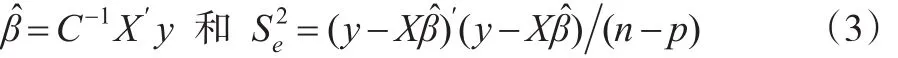
其中C=X′X。

当研究者不能确定关于样本信息的等式约束条件（2）是否成立时，考虑参数的假设检验H0:r=Rβ和备择假设H1:r≠Rβ。原假设H0对应备择假设H1的似然比检验统计量为。当备择假设H1成立时，似然比检验统计量F为自由度为(q,n-p)的非中心F分布，非中心参数为(1 2)Δ ，其中

对附加信息为等式约束的线性模型（1），Judge和Bock[1]提出了基于F检验的预检验估计。结合预检验估计和岭估计，Saleh和Kibria[2]提出了基于F检验的预检验岭估计。Yuksel和Akdeniz[3]得到了基于F检验的预检验Liu估计。进一步地，Kibria和Saleh[4]提出了基于W，LR和LM检验的预检验岭估计，并对估计的偏差和均方误差等性质做了研究。Kibria和 Saleh[5]，Saleh[6]，Yang 和 Xu[7]，Kibria[8]，Arashi等[9]对各类预检验估计的性质进行了研究。

本文在Yang和Chang[10]提出的两参数估计的基础上，运用预检验估计的思想，提出预检验两参数估计，新的估计包含了预检验估计，预检验岭估计和预检验Liu估计。进而，在均方误差准则下，给出预检验两参数估计优于预检验估计，预检验岭估计和预检验Liu估计的充分条件。

2 预检验两参数估计

为了克服模型（1）中的复共线性，Yang和Chang[10]提出的两参数估计为：

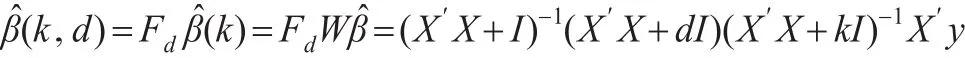
考虑带等式约束条件（2）的模型（1），结合Kaciranlar等[11]得到约束最小二乘估计的方法，提出约束两参数估计为：

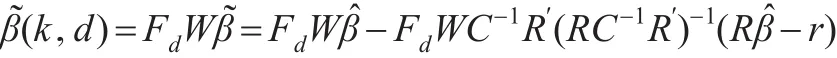
其中为约束最小二乘估计。

当对模型（1）的约束条件（2）是否成立不确定时，结合两参数估计，约束两参数估计和预检验估计的思想，得基于F检验的预检验两参数估计为：

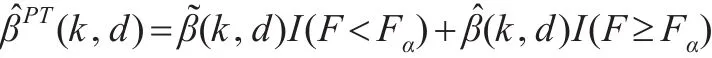
其中I(A)为事件A的示性函数，Fα表示自由度为(q,n-p)的中心F分布的上α分位数。

根据预检验两参数估计(k,d)的定义可知，当k=0 ，d=1，预检验两参数估计(0,1)即为Judge和Bock[1]提出的预检验估计；当d=1，预检验两参数估计(k,1)即为 Saleh 和 Kibria[2]提出的预检验岭估计；当k=0，预检验两参数估计(0,d)即为Yuksel和Akdeniz[3]提出的预检验Liu估计。

预检验两参数估计(k,d)的期望，偏差和均方误差为：

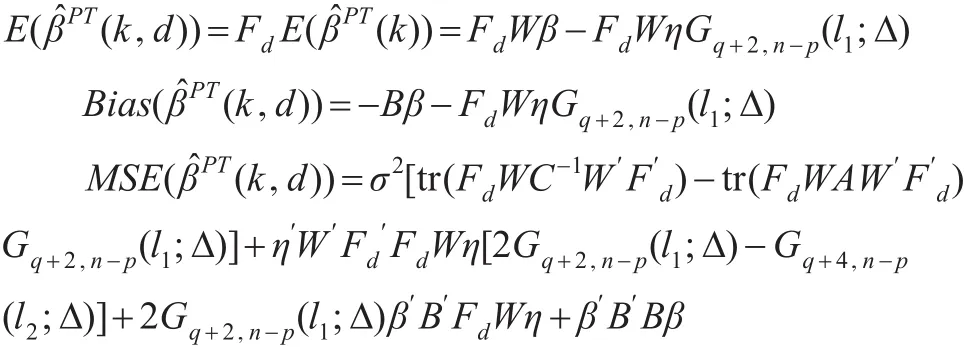
其中B=(C+I)-1[(k+1-d)C+k)](C+kI)-1，η=C-1R′(RC-1R′)-1(Rβ-r)，C(k)=X′X+kIp，A=C-1R′(RC-1R′)-1RC-1，l1=(q/(q+2))Fq,n-p(α) ，l2=(q/(q+4))Fq,n-p(α) ，Gm,n(·;Δ)表示自由度为(m,n)非中心参数为(1 2)Δ 的F分布的累计分布函数。

3 估计的优良性

在均方误差准则下，本文分别对预检验两参数估计与预检验估计，预检验岭估计和预检验Liu估计的优良性作比较。为了研究方便，引入以下记号与引理。

存在正交矩阵P，使得P′CP= Λ=diag(λ1,…,λp)，λ1≥ … ≥λp＞0 ，θ=P′β=(θ1,…θp)′，=P′η=(1,…)′，且有：

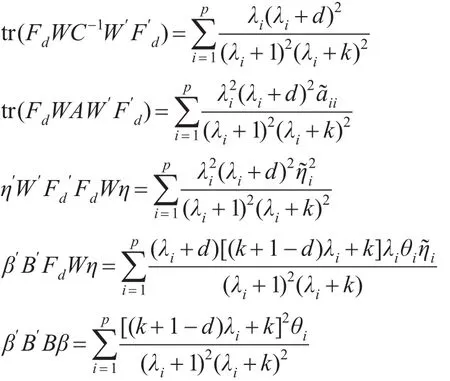
引理1[12]：设矩阵A，B均为n×n的实对称阵，且B为正定矩阵，对任意n×1的非零向量x，有成立，其中λ1(AB-1)和λn(AB-1)分别表示矩阵AB-1的最大特征值和最小特征值。

3.1 预检验两参数估计PT(k,d)与预检验估计 PT

当原假设H0成立时，预检验两参数估计(k,d)和预检验估计的均方误差之差为：

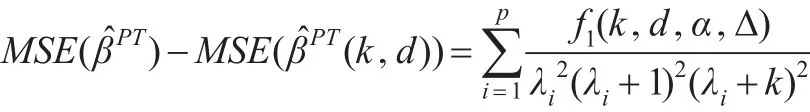
其中：

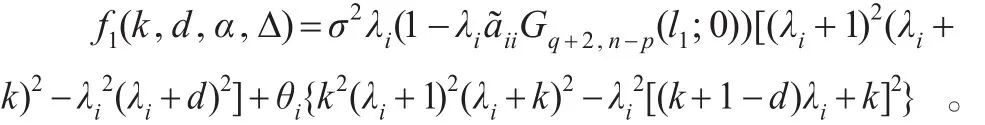
在备择假设H1成立的情况下，预检验两参数(k,d)和预检验估计的均方误差之差为：

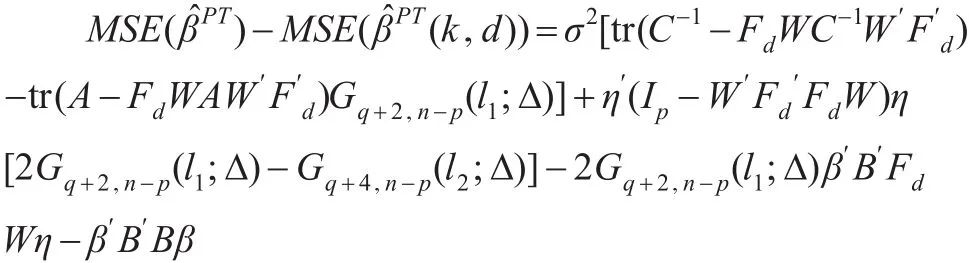
注意到Gq+2,n-p(l1;Δ)＞0 ，2Gq+2,n-p(l1;Δ)-Gq+4,n-p(l2;Δ)＞0 ，则MSE()-MSE((k,d))≥0 当且仅当：

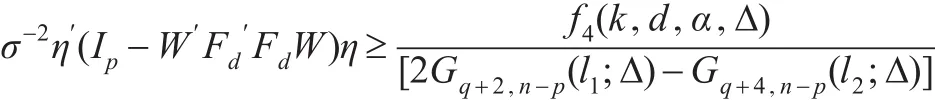
其中：

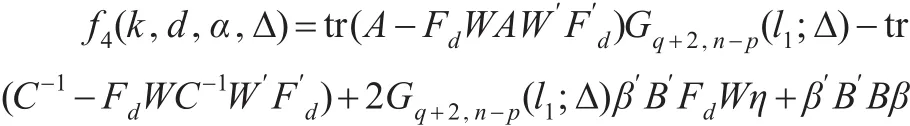
根据引理1，可知：

综合以上叙述，得以下定理：

定理1：当原假设H0成立，对k＞0和 0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验估计，即MSE()-MSE((k,d))≥0 只需 (d-1)λi2+k2λi+k2＞0成立。

定理2：当备择假设H1成立，对k＞0和0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验估计，即MSE()-MSE((k,d))≥0 只需 Δ ＞ Δ1成立。

3.2 预检验两参数估计 PT(k,d)与预检验岭估计PT(k)

当原假设H0成立时，预检验两参数估计(k,d)和预检验岭估计(k)的均方误差之差为：

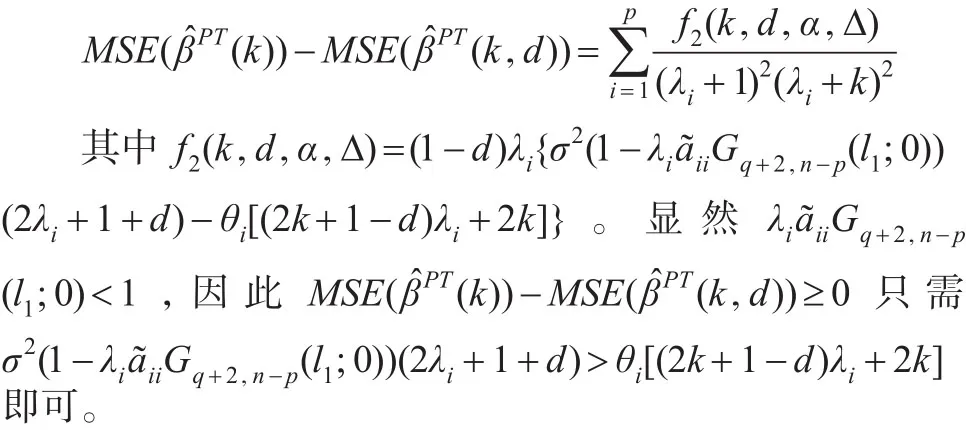
当备择假设H1成立时，预检验两参数估计(k,d)和预检验岭估计(k)的均方误差之差为：

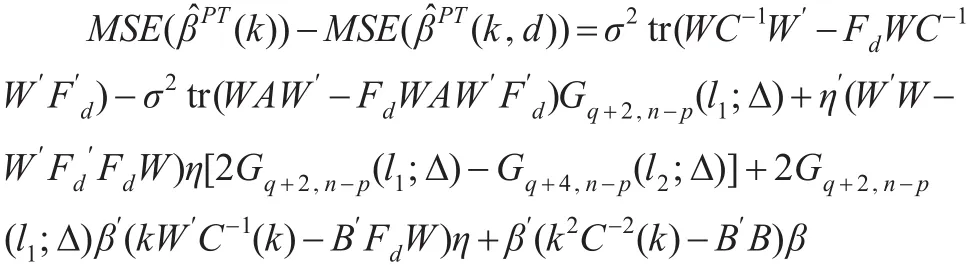
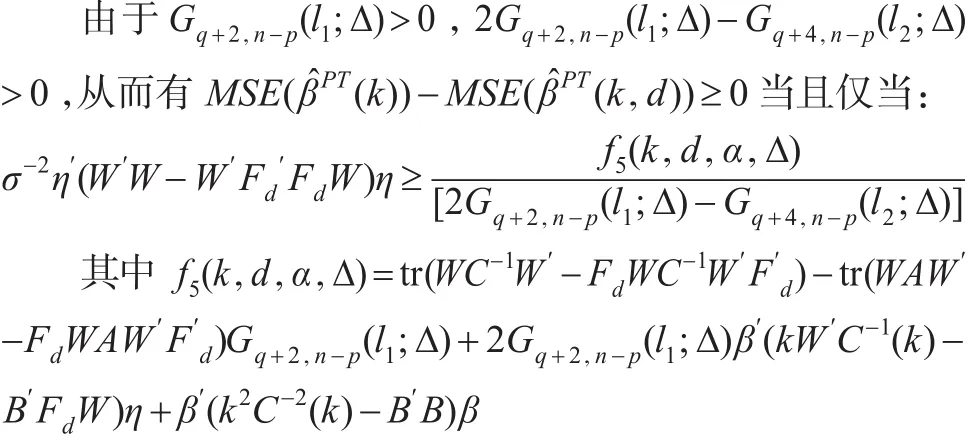
根据引理1，可知：

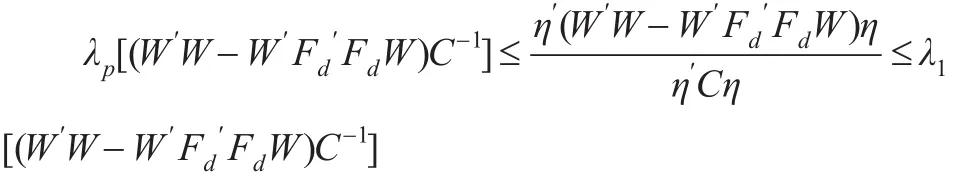
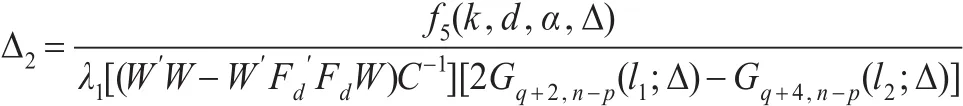
综合以上叙述，可得以下定理：

定理3：当原假设H0成立，对k＞0和 0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验岭估计(k)，即MSE((k))-MSE((k,d))≥0 只需σ2(1-λiiiGq+2,n-p(l1;0))(2λi+1+d)＞θi[(2k+1-d)λi+2k]成立。

定理4：当备择假设H1成立，对k＞0和0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验岭估计(k)，即MSE((k))-MSE((k,d))≥0 只需Δ＞Δ2成立。

3.3 预检验两参数估计PT(k,d)与预检验Liu估计PT(d)

当原假设H0成立时，预检验两参数估计(k,d)和预检验Liu估计(d)的均方误差之差为：

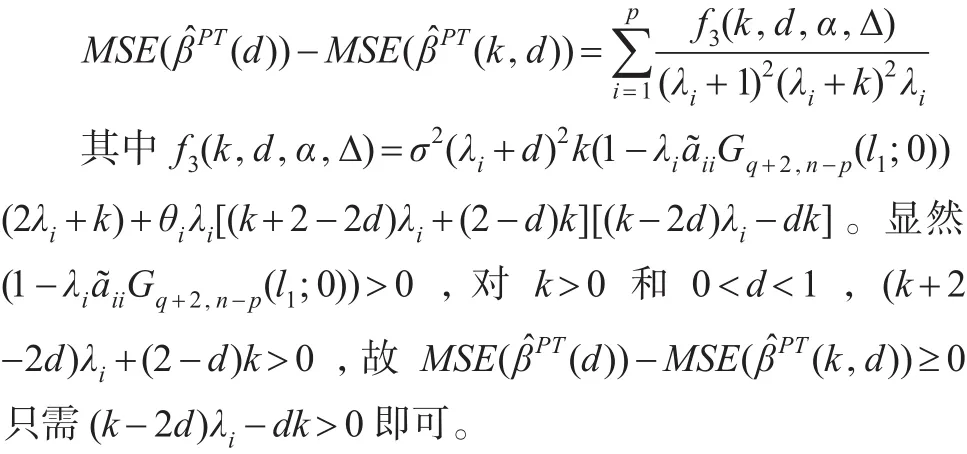
当备择假设H1成立时，预检验两参数估计(k,d)和预检验Liu估计(d)的均方误差之差为：

根据引理1，可知：

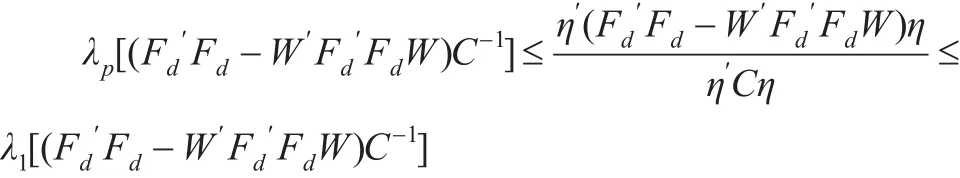
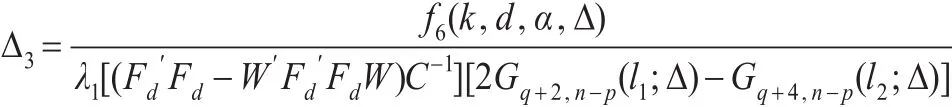
综合以上叙述，可得以下定理：

定理5：当原假设H0成立，对k＞0和 0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验Liu 估计(d)，MSE((d))-MSE((k,d)) ≥ 0 只需(k-2d)λi-dk＞0成立。

定理6：当备择假设H1成立，对k＞0和0＜d＜1，在均方误差准则下，预检验两参数估计(k,d)优于预检验Liu 估计(d)，即MSE((d))-MSE((k,d)) ≥ 0 只需Δ＞Δ3成立。

4 结论

本文首先通过运用预检验的思想，提出了线性模型参数的预检验两参数估计，可以看到预检验两参数估计包含了预检验估计，预检验岭估计和预检验Liu估计。最后，在均方误差准则下，给出了预检验两参数估计优于预检验估计，预检验岭估计和预检验Liu估计的充分条件。因此，预检验两参数估计在理论和应用上都是有意义的。

[1]Judge G G,Book M E.The Statistical Implications of Pre-test and Stein-rule Estimators in Econometrics[M].Amsterdam:North-Holland Publishing Company,1978.

[2]Saleh A K,Md E,Kibria B M G.Performances of Some New Preliminary Test Ridge Regression Estimators and Their Properties[J].Com-munications in Statistics-Theory and Method,1993,(22).

[3]Yuksel G,Akdeniz F.Properties of Some New Preliminary Test Liu Estimators and Comparisons With the Usual Preliminary Test Estimators[J].Journal of Statistical Research,2001,(35).

[4]Kibria B M G,Saleh A K,Md E.Effect of W,LR,and LM tests on the Performance of Preliminary Test Ridge Regression Estimators[J].Journal of the Japan Statistical Society,2003,(33).

[5]Kibria B M G,Saleh A K Md E.Preliminary Test Ridge Regression Estimators With Student’S T Errors and Conflicting Test Statistics[J].Metrika,2004,(59).

[6]Saleh A K,Md E.Theory of Preliminary Test and Stein-type Estimation With Applications[M].New York:John Wiley,2006.

[7]Yang H,Xu J.Preliminary Test Liu Estimators Based on the Conflicting W,Lr and Lm Tests in a Regression Model With Multivariate Student-t Error[J].Metrika,2011,(73).

[8]Kibria B M G.Some Liu and Ridge-type Estimators and Their Properties and the Ill-conditioned Gaussian Linear Regression Model[J].Journal of Statistical Computation and Simulation,2012,(82).

[9]Arashi M,Kibria B M G,Norouzirad M,et al.Improved Preliminary Test and Stein-rule Liu Estimators for the Ill-conditioned Elliptical Linear Regression Model[J].Journal of Multivariate Analysis,2014,(126).

[10]Yang H,Chang X.A New Two-parameter Estimator in Linear Regression[J].Communications in Statistics-Theory and Method,2010,(39).

[11]Kaciranlar S,Sakallioglu S,Akdeniz F,et al.A New Biased Estimator In Linear Regression and a Detailed Analysis of the Widely-analysed Dataset on Portland Cement[J].Sankhya,1999,(61).

[12]Anderson T W.An Introduction to Multivariate Statistical Analysis(2nd ed)[M]New York：John Wiley,1984.