基于思维进化算法径向基函数神经网络的土壤有机质空间异质性研究
2018-03-21江叶枫
江叶枫,郭 熙
(江西农业大学 江西省鄱阳湖流域农业资源与生态重点实验室,江西 南昌 330045)
受生物[1]、气候[2]、母质[3]和地形[4]等因素影响,土壤性质具有高度的空间异质性。即使在相邻位置,土壤性质也会受复杂的环境因素影响而产生较大差异[5-6]。对土壤性质空间异质性的充分了解不仅是有效管理土壤、科学规划土地利用和精准农业施肥的基础[7],而且可为农业生产、生态环境保护和土壤质量的修复与改善提供重要依据。目前,基于实地采样获取的土壤性质空间分布信息远不能满足土壤性质空间变异研究和环境保护的需要。因此,快速准确地获取区域土壤性质空间变异特征的研究方法——空间插值技术日益受到越来越多国内外学者的关注和重视。
目前,应用于土壤性质的空间插值方法主要有反距离加权法[8-9]、Fisher判别法[10]、趋势面分析法[11]、样条函数法[12]和克里格法[13-14]等,但这些方法前提条件多、主观性强、插值精度低,在实际应用和理论上还有诸多缺陷[5,7]。其中,应用最普遍的普通克里格法(ordinary Kriging)有3个重要前提[15],在实际应用中有许多情况因不满足前提条件而无法进行克里格插值。普通克里格法对土壤性质空间分布突变的区域难以表述,突变区域信息丢失严重[16]。同时,克里格插值的平滑效应也会在一定程度上使得局部土壤性质再表达存在不确定性[17-18]。为解决这一问题,学者们将人工神经网络引入土壤性质空间分布预测中[19-20]。径向基函数神经网络(radial basis function neural network, RBFNN)已经被证实是一种有效且精确的空间插值方法[21-22],因具有极强的非线性逼近能力,在土壤性质的空间分布预测中受到越来越多关注。RBFNN应用的关键在于权值和结构的优化[23]。部分学者尝试利用遗传算法对RBFNN进行初始权值和结构优化[17-18],但由于遗传算法本身的结构问题,依然存在易早熟问题,同时其变异和交叉算子具有双重性,有可能破坏原有基因[24],导致空间插值精度存在不确定性。本研究选取的思维进化算法(mind evolutionary computation, MEC)[25-26]对RBFNN的初始权值和网络结构进行优化。MEC通过模拟人类思维进化过程,设计出有效的趋同和异化算子。该算法具有极强的局部和全局寻优能力,在遗传算法求解存在早熟问题及解决数值和非数值优化方面显示出独特的优越性[24],但将其用于土壤性质的插值模型研究在国内外尚相对较少。
土壤有机质是评价土壤质量的重要指标,是植物矿物质营养和有机质营养的主要来源[27]。受结构性因素和随机性因素的共同作用,土壤有机质在空间分布上往往表现出较大的空间异质性[28-29]。本研究以江西省万年县耕地表层(0~20 cm)土壤有机质为研究对象,以地理坐标和邻近信息作为网络输入,运用MEC优化RBFNN的隐含层节点数、扩展常数等参数,建立基于MEC的RBFNN空间插值方法(MECRBF),并与未优化的RBFNN方法(RBF-Near,以地理坐标和邻近信息为网络输入)和普通克里格方法进行插值结果误差比较,旨在为县域尺度上更加准确地获取土壤性质空间异质性信息提供方法参考。
1 材料与方法
1.1 研究区概括
研究区位于江西省万年县,总面积1 141 km2,地理坐标介于28°30′~28°54′N、116°46′~117°15′E之间,年均降水量1 766 mm,年均无霜期263 d,海拔14~650 m,气候湿润温和,日照充足,素有“鱼米之乡”之称。研究区主要地貌类型为平原,丘陵与山地较少。土地利用类型以耕地和林地为主(图1-a)。土壤类型主要有红壤和水稻土。成土母质包括泥质岩类风化物、石英岩类风化物、碳酸岩类风化物和第四纪红色黏土。
1.2 土壤采样与数据处理
土壤样品采集于2014年8月。在考虑地形部位的基础上,采用“S”形采样、多点混合的方法采集耕地表层(0~20 cm)土壤样品,经充分混合,最后留取1 kg土样,得到960个耕地表层土壤样品(图1-b)。土壤样品经自然风干后,带回实验室磨碎过筛,采用重铬酸钾(K2Cr2O7)油浴加热测定土壤有机质含量[30]。采用阈值法对采样点数据的土壤有机质进行异常值处理(3倍标准差)[31]。后续研究均采用剔除异常值后的数据,总样点共计954个:随机均匀选取4/5样点作为建模点(763个)用于插值;剩下1/5样点作为验证点(191个,不参与插值过程,只在精度分析中出现)用于验证插值精度。

图1 土壤样点分布Fig.1 Distribution of soil sampling sites
1.3 邻近信息提取
利用四方位搜索法(four-direction search method)获取采样点附近土壤有机质含量。四方位搜索法基于反距离加权算法思想和空间自相关理论,根据采样点之间的距离越近影响越大、距离越远影响越小的思想,以采样点为坐标原点、变程a(半方差函数中土壤有机质的变程)为半径,在每个象限内选择一个邻近点土壤有机质含量值P1、P2、P3、P4。四方位搜索算法步骤如下。
1)在Matlab中新建一个Points[]文件,导入所有采样点地理坐标(x,y)和土壤有机质含量(z);
2)从文件中随机抽取一个点,赋值给Mi;
3)在Point[]文件剩余点中随机抽取一个点,赋值给Ni;
4)计算M、N2点之间的欧氏距离,设为d,令VTemp1=VTemp2=VTemp3=VTemp4=a,若d>a,则回到步骤3);
5)若Ni(x)>Mi(x)、Ni(y)≥Mi(y),且d≤VTemp1,则VTemp1=d,P1=Ni(z);
6)若Ni(x)≤Mi(x)、Ni(y)>Mi(y),且d≤VTemp2,则VTemp2=d,P2=Ni(z);
7)若Ni(x) 8)若Ni(x)≥Mi(x)、Ni(y) 9)重复步骤2)~8),直至遍历Point[]文件中所有点,将P1、P2、P3、P4存放在文本中。 四方位搜索法在Matlab R2014a中通过编程实现,出现的空值由其他象限的平均值进行计算。其中:P1、P2、P3、P4分别代表以采样点为坐标原点,4个象限内离采样点最邻近点的土壤有机质含量值;Mi和Ni表示采样点的地理坐标,Mi(x)和Ni(x)表示经度,Mi(y)和Ni(y)表示纬度。 土壤属性空间插值实际上就是根据已知采样点寻找空间曲面的映射函数,然后应用这种映射函数对研究区表面进行拟合。RBFNN具有极强的映射能力,将自变量(本研究为地理坐标和建模点的邻近信息)作为网络的输入层、因变量(本研究为建模点土壤有机质含量)作为网络的输出层,通过RBFNN建立起自变量与因变量的映射关系,从而实现对土壤属性的空间插值。本研究采用MEC对网络的隐含层节点数和扩展常数等参数进行优化。具体实现步骤如下。 1)RBFNN参数改写。将RBFNN的隐含层节点数和扩展常数以函数变量的形式表达,以供最开始进行MEC时调用。 2)产生初始结构群体。设RBFNN结构最大隐含层数目为n(训练样本数),每一隐含层最大隐含层节点数为m(隐含层节点数为0~m)。随机产生K组数作为初始结构群体,每组数包含n个元素,代表RBFNN结构(即一个个体),其中每个元素隐含层节点数均以相同概率P=1/(m+1)从0~m中选取。 3)针对每个群体产生权值并训练。针对每一个个体,在(0~1)中均匀产生L组随机数作为初始群体的权值,然后以目标输出与网络输出之间的均方误差倒数作为个体的得分。将得分高的(A+B)个个体作为优胜者,以前A个优胜者为中心产生A个优胜子群体,以后B个优胜者为中心产生B个临时子群体。每个子群体包含W个个体,即子群体的规模为W=L/(A+B)。在每个子群体中计算每个个体的得分,以得分最高者作为这个子群体的得分。 4)子群体异化。将每个优胜者的得分张贴到全局公告板上供其余个体学习,产生新的子群体,完成优胜和临时子群体的更新,得到全局最优个体和得分。被替代的子群体在进化信息和全局公告板的指导下形成新的临时子群体,并与其他临时子群体进行全局竞争。 5)较优RBFNN结构的获取。当某一结构达到最大迭代次数仍未满足要求时被释放,在满足要求的结构中根据结构简单且性能好的原则找到优胜结构(径向基函数网络参数),即个体的得分。 6)MECRBF空间插值实现。将优化的隐含层节点数和扩展常数输入到RBFNN中,求出建模集和验证集的预测结果,并在[-1,1]之间生成覆盖万年县的二维网格,每个内插点对应一组地理坐标数据,将其作为训练好的神经网络的输入,利用sim函数仿真出每组地理坐标对应的土壤有机质预测结果后进行反归一化。利用meshgrid命令生成研究区空间分布(30 m)。将预测结果保存在txt文本中,导入ArcGIS 10.2转成栅格文件,生成基于MECRBF的空间插值图。 7)RBF-Near参数的确定与普通克里格法参数的确定。以验证样点预测结果的均方根误差最小为约束条件,将RBF-Near模型的隐含层节点数和扩展常数设为10和1。普通克里格法在GS+(version 7)中对半方差函数进行拟合,最后得到的最优模型为线性模型,拟合度0.820,块金值与基台值之比为83.69%,土壤有机质的变程为22.47 km。 8)结果检验。以均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MRE)对建模点和验证点的预测值与实测值进行对比分析,得出精度评价结果。 (1) (2) (3) 如表1所示,研究区土壤有机质含量的平均值为33.33 g·kg-1,值域范围为9.81~56.31 g·kg-1。从K-S检验可以判断,土壤有机质分布接近正态分布。土壤有机质的变异系数在10%~100%之间,表现为中等程度的变异性。对建模集和验证集进行常规统计分析,变异系数分别为23.18%和23.34%,均呈中等程度变异。 在GS+软件中对土壤有机质进行半变异函数拟合,用半变异函数描述其空间变异性。结果显示,土壤有机质的最优模型为线性模型,拟合系数为0.820,拟合效果好。土壤有机质的块金效应值(随机性因素引起的空间变异占系统总空间变异的比值)为83.69%,表明土壤有机质空间变异主要受随机性因素影响,呈弱空间相关性。变程22.47 km,表明土壤有机质空间自相关范围较大。 表1土壤有机质的描述性统计 Table1Descriptive statistics characteristics of soil organic matter 样本Samples样点数Number最大值Maximum/(g·kg-1)最小值Minimum/(g·kg-1)平均值Mean/(g·kg-1)标准差SD/(g·kg-1)变异系数CV/%全部样点Allpoints954563198133337742322建模点Modelingpoints7635631101733477762318验证点Validationpoints191531198132777652334 SD, Standard deviation; CV, Coefficient of variation. 为说明MECRBF在土壤有机质空间分布模拟过程中的拟合能力,将其与RBF-Near和普通克里格方法进行对比。通过建立采样点的预测值与实测值之间的一元回归方程决定系数(R2)来判断这3种方法拟合能力的高低,并对3种方法的预测值进行最小显著性(LSD)检验。 图2与图3分别是土壤有机质在3种方法下建模点与验证点预测值和实测值的散点图。从图2可以看出,MECRBF方法的决定系数达到0.908 3,拟合能力优于其他方法,且预测结果与其他方法有显著差异(RBF-Near,P=0.002;普通克里格法,P=0.004)。RBF-Near与普通克里格法的拟合系数分别为0.581 4和0.324 8,LSD检验结果显示这2种方法的预测结果间没有显著差异(P=0.825)。从图3可以看出,MECRBF方法的决定系数达到0.718 1,拟合能力优于其他方法,且与其他两种方法的结果有显著差异(RBF-Near,P=0.001;普通克里格法,P=0.000 1)。RBF-Near与普通克里格法的预测结果经LSD检验显示无显著差异(P=0.278)。以上结果说明,没有进行网络参数优化的神经网络方法(RBF-Near)虽然在全局部范围内有较好的映射能力,但其逼近效果与普通克里格法相比并无显著改善,在局部方面还有很大的提升空间。 图2 不同方法下建模样点散点图Fig.2 Scatter of modeling samples under different methods 图3 不同方法下验证样点散点图Fig.3 Scatter of validation points under different methods 从表2可以看出:在建模点预测中,MECRBF的RMSE、MAE、MRE较RBF-Near分别降低了2.51 g·kg-1、1.98 g·kg-1、6.67百分点,差异显著(P=0.002),较普通克里格法分别减低了3.87 g·kg-1、2.91 g·kg-1、9.97百分点,亦差异显著(P=0.004);在验证点预测中,MECRBF的RMSE、MAE、MRE较RBF-Near分别降低了0.50 g·kg-1、0.39 g·kg-1、1.40百分点,差异显著(P=0.001),较普通克里格法分别降低了2.59 g·kg-1、1.89 g·kg-1、7.76百分点,差异显著(P=0.000 1)。MECRBF的插值精度优于其他方法,说明经过MEC优化的RBFNN在一定程度上提高了网络的泛化能力。 运用RBF-Near和MECRBF方法预测研究区土壤有机质的空间分布,按照30 m分辨率利用meshgrid命令生成,在ArcGIS 10.2中显示;同时,运用普通克里格法对土壤有机质建模点进行插值,得到分布模拟图(分辨率30 m)。由图4可以看出,3种方法在模拟土壤有机质空间分布时均呈“两边高,中间低”的总体趋势,高低值区域分布大致相同。普通克里格法空间分布模拟图中西北和正南方向土壤有机质含量最高,预测土壤有机质在30~36 g·kg-1之间所占范围最大,预测结果较平滑,难以体现土壤有机质空间分布的异质性。RBF-Near在整个研究区空间分布模拟结果中出现了明显的高值斑块和低值区域,高低值之间的变化较突兀,可体现土壤有机质空间分布的异质性信息,但在局部范围内难以描述土壤有机质的空间变异信息,预测土壤有机质小于33 g·kg-1的区域面积所占比例大。MECRBF预测土壤有机质的变化趋势更接近自然,结合土地利用现状可知,高值区域分布在耕地较为密集的西北区,受耕种和人为调节等因素影响,土壤有机质要高于其他区域,说明MECRBF预测的土壤有机质空间分布可信度较高。MECRBF预测土壤有机质在30~36 g·kg-1之间所占范围最大,高低值呈带状分布,突出了数据的波动性,较RBF-Near在土壤有机质空间分布预测中有较大改善。说明MECRBF通过不断的趋同和异化操作在一定程度上克服了由于初始权值和网络结构的设置无法得到全局与局部最优解的缺点,改善了RBFNN的收敛精度和速度,能够在尊重原始观测数据的基础上更加客观地呈现土壤有机质空间分布的异质性。 表2土壤有机质预测方法精度对比 Table2Precision comparison of different methods 方法Method建模点ModelingpointsRMSEMAEMRE验证点ValidationpointsRMSEMAEMRE普通克里格OrdinaryKriging63949016637385612119RBF⁃Near50339713335294111483MECRBF2521996664793721343 图4 不同方法下土壤有机质空间分布预测结果Fig.4 Maps of soil organic matter by different methods 本研究以万年县为案例区,采用MECRBF对当地耕地表层土壤有机质的空间异质性进行研究,结果表明,案例区土壤有机质含量在9.81~56.33 g·kg-1之间,平均值为33.33 g·kg-1,变异系数为23.22%,呈中等变异。对191个验证样点预测结果的误差分析表明,MECRBF对土壤有机质预测结果的RMSE、MAE、MRE较RBF-Near分别降低了0.50 g·kg-1、0.39 g·kg-1、1.40百分点,差异显著,较普通克里格法分别降低了2.59 g·kg-1、1.89 g·kg-1、7.76百分点,差异显著。 对建模点的拟合结果表明,以邻近信息和地理坐标为网络输入的RBF-Near对建模点的拟合系数明显高于普通克里格法。徐剑波等[18]引入邻近信息和地理坐标为网络输入的RBFNN对土壤属性的空间插值结果表明,RBFNN具有较强的映射能力,这和本研究结果一致。这是因为邻近信息能更好地揭示土壤属性空间分布的局部变化特征,能在提高映射能力的同时更加真实地反映土壤属性空间变异特征。在本研究中,通过引入MEC对RBFNN参数进行优化,其拟合精度较RBF-Near有显著提高。 对验证点的插值误差结果表明,RBF-Near的预测能力明显优于普通克里格法。普通克里格法虽然能够通过邻近相关采样点土壤有机质权重来预测未知点土壤有机质含量,并对预测结果给出误差,但该方法假设研究区为匀值空间,运用条件多,受主观影响大,制图效果和预测精度还不很理想。而MECRBF对网络的隐含节点数和扩展常数等参数进行优化,提高了RBFNN的泛化能力,克服了RBFNN易陷入全局最优的缺点,因而具有更好的预测能力。 从插值效果图来看,普通克里格法与2种RBFNN方法插值得到的土壤有机质空间分布图均呈“两边高、中间低”的总体趋势,但3种方法的效果图局部差异明显:普通克里格法高低值分布较平滑,难以体现土壤有机质空间异质性的细节信息;RBF-Near在一定程度上克服了普通克里格法的平滑效应,高低值分布较突兀,比较符合土壤有机质空间分布的异质性;MECRBF插值模拟图不仅高低值分布明显,而且突出了区域化变量的波动性,同时更加真实地反映了数据的变异性。这是因为MEC的趋同和异化算子通过不断进行“开采”和“勘探”,在局部和全局寻找最优解,同时其记忆机制和定向机制使得进化方向始终朝着最优方向进行。MEC提高了RBFNN的泛化能力,改进了网络的收敛速度和收敛精度,使得MECRBF对土壤有机质空间异质性的描述要优于其他2种方法。 总体来看,普通克里格法对研究区验证点的拟合能力低于2种神经网络方法,对土壤有机质空间异质性的描述能力亦不如2种神经网络方法。这主要是由于神经网络具有极强的映射能力,能以任意精度逼近任意连续函数,因此对土壤有机质的拟合效果、预测精度和异质性的描述均较为理想。但是RBFNN插值实际上是一种基于全局信息的插值过程。前人研究表明,仅基于地理坐标的RBFNN方法只能在全局范围内反映土壤有机质的空间分布特征,并不能在局部描述其空间异质性[5,32]。本研究将邻近信息纳入RBFNN的输入层,对研究区土壤有机质空间分布和异质性的描述较普通克里格法有很大改善。虽然2种方法都是基于建模点提供的土壤有机质信息,但普通克里格法由于理论假设、前提条件多、半变异函数的拟合曲线受主观因素影响大,以及预测精度偏低等,导致2种方法在土壤有机质空间异质性描述时产生较大差异。在应用RBFNN进行土壤性质的空间异质性研究中,初始权值和网络参数的设定会影响土壤性质的空间插值精度与异质性的表达详细程度。本研究利用MEC优化RBFNN的隐含层节点数和扩展常数等参数,建立的MECRBF在土壤有机质的空间插值精度和异质性描述中较RBF-Near和普通克里格法取得了更好的结果。该方法可为今后土壤性质的空间异质性研究提供方法参考。 本文只是对RBFNN的初始权值和网络结构进行了优化,在网络学习规则方面仍有不足,后续研究可结合重采样算法对网络学习规则进行优化。同时,RBFNN无法像地统计学那样定量描述土壤有机质的空间自相关性,这是其不足之处。通过引入更多的变量(如环境因子、土壤结构性因子,甚至时间因子等)作为网络的输入来预测土壤性质的空间分布,可以进一步提高其描述土壤空间分布异质性的准确性。 [1] MCBRATNEY A B, PRINGLE M J. Estimating average and proportional variograms of soil properties and their potential use in precision agriculture[J].PrecisionAgriculture, 1999, 1(2): 125-152. [2] DAI W, HUANG Y. Relation of soil organic matter concentration to climate and altitude in zonal soils of China[J].Catena, 2006, 65(1):87-94. [3] SARKAR S, ROY A K, MARTHA T R. Soil depth estimation through soil-landscape modelling using regression Kriging in a Himalayan terrain[J].InternationalJournalofGeographicalInformationScience, 2013, 27(12):2436-2454. [4] GUO P T, LIU H B, WU W. Spatial prediction of soil organic matter using terrain attributes in a hilly area[C]. 2009 International Conference on Environmental Science and Information Application Technology. Los Alamtios, CA: IEEE Computer Society, 2009: 759-762. [5] 李启权, 王昌全, 岳天祥, 等. 基于RBF神经网络的土壤有机质空间变异研究方法[J].农业工程学报, 2010, 26(1): 87-93. LI Q Q, WANG C Q, YUE T X, et al. Method for spatial variety of soil organic matter based on radial basis function neural network[J].TransactionsoftheCSAE, 2010, 26(1): 87-93. (in Chinese with English abstract) [6] VASQUEZ P J R, BAENA GARCIA D, MENJIVAR FLORES J C. Spatial variability of physical and chemical properties in soils of the experimental farm in the Magdalena University (Santa Marta, Colombia)[J].ActaAgronómica, 2010, 59(4):449-456. [7] XU S, ZHAO Y, SHI X, et al. Map scale effects of soil databases on modeling organic carbon dynamics for paddy soils of China[J].Catena, 2013, 104(2):67-76. [8] BARTIER P M, KELLER C P. Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW)[J].Computers&Geosciences, 1996, 22(7):795-799. [9] ZHOU J, SHA Z. A new spatial interpolation approach based on inverse distance weighting: case study from interpolating soil properties[M]//Geo-informatics in resource management and sustainable ecosystem. Berlin: Springer, 2013:623-631. [10] 刘勋鑫, 王翠红, 廖超林, 等. 土壤重金属特性空间变异性方法研究[J]. 农业网络信息, 2007 (6):106-108. LIU X X, WANG C H, LIAO C L, et al. The research on the methods of heavy metal spatial variation in soil[J].AgricultureNetworkInformation, 2007 (6): 106-108. (in Chinese with English abstract) [11] WANG X J, ZHANG Z P. A comparison of conditional simulation, Kriging and trend surface analysis for soil heavy metal pollution pattern analysis[J].JournalofEnvironmentalScience&HealthPartA, 1999, 34(1):73-89. [12] VOLTZ M, WEBSTER R. A comparison of Kriging, cubic splines and classification for predicting soil properties from sample information[J].EuropeanJournalofSoilScience, 1990, 41(3):473-490. [13] SHAHBEIK S, AFZAL P, MOAREFVAND P. Comparison between ordinary Kriging (OK) and inverse distance weighted (IDW) based on estimation error. Case study: dardevey iron ore deposit, NE Iran[J].ArabianJournalofGeosciences, 2014, 7(9): 3693-3704. [14] GIRALDO R, DELICADO P, MATEU J. Ordinary Kriging for function-valued spatial data[J].EnvironmentalandEcologicalStatistics, 2011, 18(3):411-426. [15] 史舟, 李艳. 地统计学在土壤学中的应用[M]. 北京:中国农业出版社, 2006. [16] 沈掌泉, 施洁斌, 王珂, 等. 应用集成BP神经网络进行田间土壤空间变异研究[J]. 农业工程学报, 2004, 20(3):35-39. SHEN Z Q, SHI J B, WANG K, et al. Spatial variety of soil properties by BP neural network ensemble[J].TransactionsoftheCSAE, 2004, 20(3): 35-39. (in Chinese with English abstract) [17] 董敏, 王昌全, 李冰, 等. 基于GARBF神经网络的土壤有效锌空间插值方法研究[J]. 土壤学报, 2010, 47(1): 42-50. DONG M, WANG C Q, LI B, et al. Study on soil available zinc with GA-RBF-neural-network-based spatial interpolation method[J].ActaPedologicaSinica, 2010, 47(1): 42-50. (in Chinese with English abstract) [18] 徐剑波, 宋立生, 夏振, 等. 基于GARBF神经网络的耕地土壤有效磷空间变异分析[J]. 农业工程学报, 2012, 28(16): 158-165. XU J B, SONG L S, XIA Z, et al. Spatial variability of available phosphorus for cultivated soil based on GARBF neural network[J].TransactionsoftheCSAE, 2012, 28(16): 158-165. (in Chinese with English abstract) [19] WU W, TANG X P, GUO N J, et al. Spatiotemporal modeling of monthly soil temperature using artificial neural networks[J].TheoreticalandAppliedClimatology, 2013, 113(3):481-494. [20] 李启权, 王昌全, 张文江, 等. 基于神经网络模型和地统计学方法的土壤养分空间分布预测[J]. 应用生态学报, 2013, 24(2): 459-466. LI Q Q, WANG C Q, ZHANG W J, et al. Prediction of soil nutrients spatial distribution based on neural network model combined with geostatistics[J].ChineseJournalofAppliedEcology, 2013, 24(2): 459-466. (in Chinese with English abstract) [21] GHOSH-DASTID S, ADELI H, DADMEHR N. Principal component analysis-enhanced cosine radial basis function neural network for robust epilepsy and seizure detection[J].IEEETransactionsonBio-MedicalEngineering, 2008, 55(2):512-518. [22] LEUNGH, LOT, WANG S. Prediction of noisy chaotic time series using an optimal radial basis function neural network[J].IEEETransactionsonNeuralNetworks, 2001, 12(5):1163-1172. [23] 陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2013. [24] ZHANG J, YANG Y P, ZHANG J M. A MEC-BP-adaboost neural network-based color correction algorithm for color image acquisition equipments[J].Optik, 2016, 127(2):776-780. [25] 孙承意, 谢克明, 程明琦. 基于思维进化机器学习的框架及新进展[J]. 太原理工大学学报, 1999, 30(5): 453-457. SUN C Y, XIE K M, CHENG M Q. Mind-evolution-based machine learning framework and new development[J].JournalofTaiyuanUniversityofTechnology, 1999, 30(5): 453-457. (in Chinese with English abstract) [26] SUN C Y, SUN Y, WEI L J. Mind-evolution-based machine learning: frame work and the implementation of optimization[C]//Proceedings of IEEE International Conference on Intelligent Engineering Systems (INES′98). Vienna, Austria, 1998: 355-359. [27] 李启权, 王昌全, 岳天祥, 等. 基于定性和定量辅助变量的土壤有机质空间分布预测: 以四川三台县为例[J]. 地理科学进展, 2014, 33(2):259-269. LI Q Q, WANG C Q, YUE T X, et al. Prediction of distribution of soil organic matter based on qualitative and quantitative auxiliary variables: a case study in Santai County in Sichuan Province[J].ProgressinGeography, 2014, 33(2): 259-269. (in Chinese with English abstract) [28] 宋莎, 李廷轩, 王永东, 等.县域农田土壤有机质空间变异及其影响因素分析[J].土壤,2011,43(1):44-49. SONG S, LI T X, WANG Y D, et al. Spatial variability of soil organic matter and its influencing factors at county scales[J].Soils, 2011, 43(1):44-49. (in Chinese with English abstract) [29] 黄安, 杨联安, 杜挺,等. 基于多元成土因素的土壤有机质空间分布分析[J]. 干旱区地理, 2015, 38(5):994-1003. HUANG A, YANG L A, DU T, et al. Spatial distribution of the soil organic matter based on multiple soil factors[J].AridZoneResearch, 2015, 38(5):994-1003. [30] 张甘霖, 龚子同. 土壤调查实验室分析方法[M]. 北京: 科学出版社, 2012: 8-66. [31] 王政权. 地统计学及在生态学中的应用[M].北京: 科学出版社, 1999. [32] 李启权, 王昌全, 张文江, 等. 丘陵区土壤有机质空间分布预测的神经网络方法[J].农业环境科学学报, 2012, 31(12):2451-2458. LI Q Q, WANG C Q, ZHANG W J, et al. Predict the spatial distribution of soil organic matter for a hilly region with radial basis function neural network[J].JournalofAgro-EnvironmentScience, 2012,31(12):2451-2458. (in Chinese with English abstract)1.4 插值
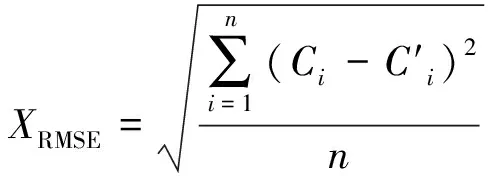

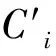
2 结果与分析
2.1 土壤有机质的描述性统计特征
2.2 半变异函数分析

2.3 拟合能力对比分析


2.4 插值精度分析
2.5 空间分布模拟结果


3 讨论
