3种ET0计算方法在海南省的适用性比较

朱潇枭，方朝阳，罗玉峰

(武汉大学水利水电学院，武汉 430072)

海南省处于我国最南端，属热带季风性气候，是发展热带特色高效农业的黄金宝地[1]。海南省虽然降雨充沛，但降雨量在地域和时间上分布不均，且可直接用于农业生产的降雨量较少，严重制约了海南省热带特色农业的发展[1-3]。另一方面，海南是孤岛，淡水资源只能由本省供给，加之全省地形中部高、四周低，淡水资源贮藏量小[2]，因此，推广农业节水灌溉对海南省的农业发展至关重要[1-4]。

参考作物需水量ET0是准确估算作物需水量的关键，对指导作物的适量灌溉具有重要意义[5,6]。联合国粮农组织(FAO)推荐使用Penman-Monteith公式作为标准计算方法[7]，但Penman-Monteith公式需要较多气象数据，故在资料不足的地区难以推广。国内外学者以Penman-Monteith法为基准，对多种ET0计算方法进行了大量研究[7-17]，但不同计算方法的适用性仍存在地域差异。国内的研究区域多数为北方地区而南方较少[11]，针对我国热带地区的研究则更少，并且不同地域适用的公式也不同。例如，谢平等[15]在湛江地区的研究中发现，Priestley-Taylor法和Irmak-Allen法在夏季相关性较好，从全年来看，Hargreaves公式在湛江地区适用性最好。郑汐等[11]认为Irmak-Allen法可作为深圳地区缺少相关气象资料条件下计算ET0较理想的替代方法。Gunston 与Batchelor[16]认为在湿润的热带气候下Priestley-Taylor法作为Penman-Monteith公式的替代方法效果较好。

本文以Penman-Montieth公式计算结果为标准，对海南省7个站点进行Priestley-Taylor法、Irmak-Allen法和Hargreaves-Samani法的适用性评价和对比分析。这有利于海南省实现农业高效节水灌溉，有利于当地热带特色农业的发展，也为ET0计算方法在我国热带地区的适用性研究提供更多理论依据。

1 资料和方法

1.1 数据资料

从“中国气象数据网”(http:∥data.cma.cn)收集了海南省7个站点2000-2014年的逐日气象数据，站点包括：儋州、海口、陵水、琼海、琼中、三亚、东方。各站点的分布位置如图1所示。收集的气象数据包括：最高气温、最低气温、平均气温、平均风速、相对湿度和日照时数共6项数据。

图1 研究站点分布

1.2 计算方法

将FAO-56Penman-Monteith(PM)公式[5]的计算结果作为评价其他公式精度的标准值。PM公式如下：

(1)

式中：Tmean为日平均气温，℃；Rn为太阳净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；γ为干湿计常数，kPa/℃；U2为距离地面2 m处的日平均风速，m/s；es和ea分别为饱和水汽压和实际水汽压，kPa；Δ为饱和水汽压与温度曲线的斜率，kPa/℃。

选用的3种ET0计算方法分别为Priestley-Taylor(PT)法[18]、Irmak-Allen(IA)法[19]和Hargreaves-Samani(HS)法[20]。

Priestley-Taylor公式：

(2)

Irmak-Allen公式：

ET0.IA=0.489+0.289Rn+0.023Tmean

(3)

Hargreaves-Samani公式：

(4)

式中：Ra为大气辐射，MJ/(m2·d)；λ为水汽化潜热，MJ/kg；Tmax和Tmin分别为最高气温和最低气温；C、E、T为Hargreaves公式的3个参数，建议值分别为0.0023、0.5、17.8。

1.3 误差分析方法

计算分析不同ET0计算方法的相关性和精度。本文以平均绝对误差MAE( Mean Absolute Error, mm/d)、平均相对误差MRE(Mean Relative Error, %)作为精度的衡量指标，其形式如下：

(6)

式中：xi为PM公式计算ET0值，mm/d；yi为其他方法计算ET0值，mm/d；n为样本数。

MAE和MRE值越小，相应的计算结果的误差和离散程度越小，精度越高。

2 结果和讨论

2.1 逐日ET0变化规律分析

图2给出了不同计算方法在2000-2014年逐日ET0计算值的变化规律。从图2可知，不同计算方法得到的逐日ET0在年内均呈现出先增后减的变化规律。12-1月份ET0最小，5-7月达到峰值后下降，出现峰值时ET0.PM的变幅较大，超过3 mm/d。在ET0达到峰值期间，PT公式计算结果与PM公式计算结果的吻合程度明显优于IA公式和HS公式。而HS公式在PM公式计算结果过大或过小时会出现较大偏差[17]，原因可能是HS公式仅基于最高和最低气温进行计算，未考虑其他气象要素对ET0值的影响，故导致误差较大。当ET0值较大时，IA公式符合较好，但在冬季出现较大偏差，这可能由于IA公式是基于湿润地区拟定[19]，而海南地区干湿分明，雨季主要集中在6-10月[2]。总体来看，PT公式计算结果与PM公式的计算结果一致性最好。

图2 不同计算方法的逐日ET0变化规律

2.2 误差分析

由表1可知，在海南大部分地区ET0计算方法的计算精度依次为PT公式>HS公式>IA公式。使用PT公式计算ET0的平均绝对误差和平均相对误差分别为0.760 mm/d和24.190%。PT公式在东方的平均相对误差16.947%，为3种计算方法在7个站点得到的平均相对误差的最小值，但平均绝对误差的最小值为HS公式在陵水的误差计算结果。HS公式在陵水的平均绝对误差为0.621 mm/d，低于PT公式在东方得到的0.630 mm/d。而在三亚地区，HS公式的平均绝对误差和平均相对误差分别为0.632 mm/d和21.743%，精度均高于PT公式和IA公式的误差计算结果。这说明，HS公式是PM公式在陵水和三亚地区的最优替代方法。相比PT和HS公式，IA公式的误差最大，平均绝对误差为0.695～0.929 mm/d，平均相对误差为22.591%～37.578%。上述结果表明，总体上，PT公式的精度最高，其次是HS公式，IA公式精度最低。

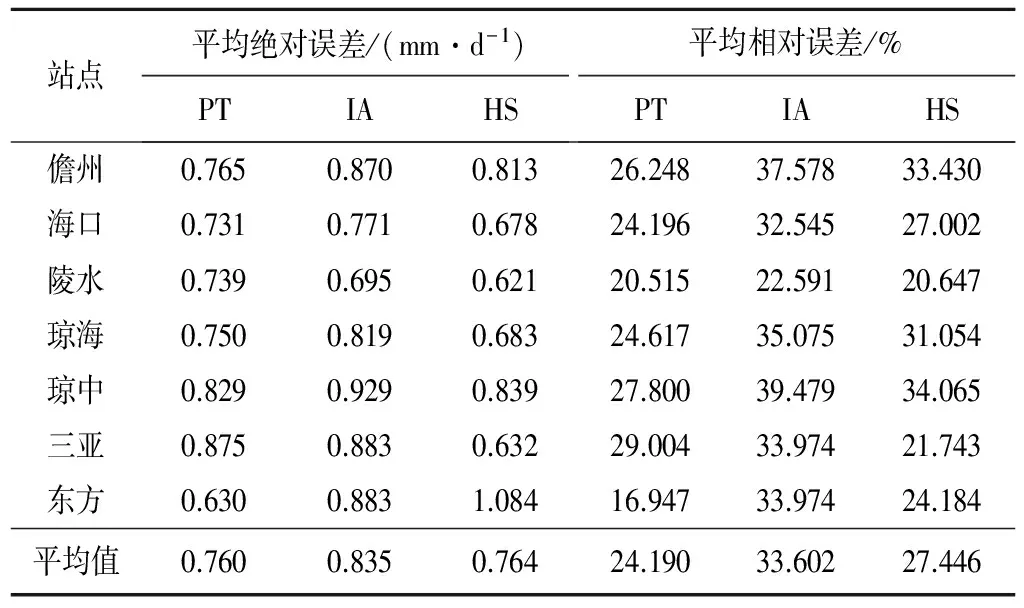
表1 不同站点不同计算方法的误差

2.3 相关性分析

如图3所示为不同计算方法与PM公式的相关性分析。PT、IA、HS公式与PM公式都具有显著的相关性，回归方程斜率分别为1.203、0.883、0.725。不同ET0计算方法在海南省的相关性依次为PT公式>IA公式>HS公式。PT公式与IA公式的相关系数(R2)分别为0.949和0.946，且PT和IA公式的散点分布较HS公式更集中。这说明，PT公式和IA公式在海南地区具有较高的相关性。

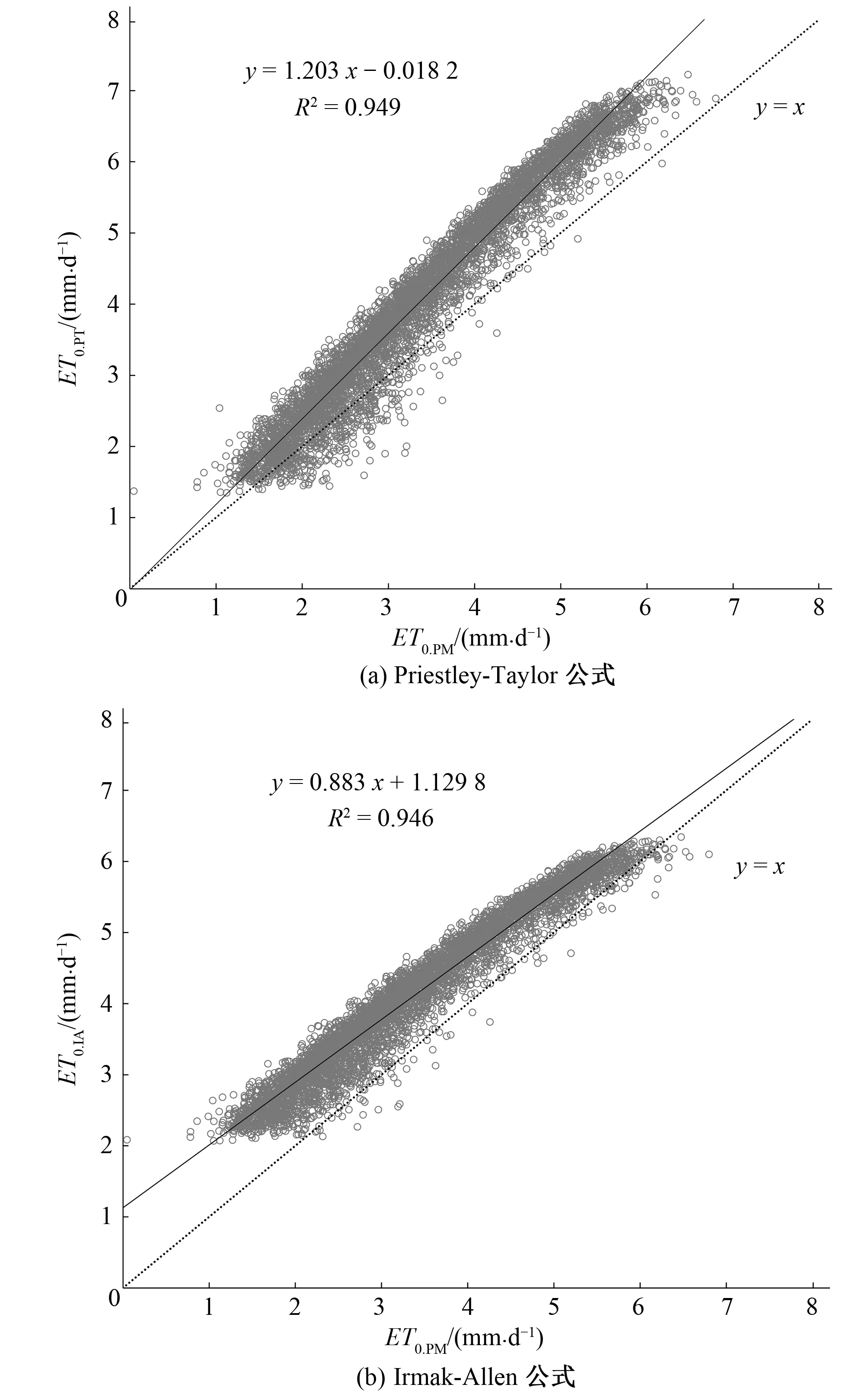
图3 不同计算方法与PM公式的相关性分析

3 结 语

(1)3种ET0计算方法在不同地区估算的ET0的年内变化与PM公式的计算值趋势相同，均为先增加后减小，在12-1月ET0值最小，峰值出现在5-7月。从全年来看，PT公式与PM公式吻合得最好。

(2)ET0计算方法在海南省的相关性依次为PT公式>IA公式>HS公式，其中PT公式和IA公式的相关系数(R2)均大于0.9。总体来看，PT公式为海南省精度最高的ET0计算方法，其平均绝对误差和平均相对误差分别为0.760 mm/d和24.190%。而HS公式是陵水和三亚地区最优的计算方法，平均绝对误差均低于0.64 mm/d，平均相对误差均低于22%。IA公式相关性较好，但整体高估了ET0值，偏差最大。因此，在所选3种计算方法中，PT公式在海南省具有最好的适用性。

[1] 王 文, 林 茂. 海南省农业节水灌溉的发展现状研究[J]. 热带农业工程, 2011,35(1):49-52.

[2] 陈政梅. 海南靠海更要节水[J]. 农机科技推广, 2005,(8):30.

[3] 罗文杰. 海南水资源的农业利用及节水农业的发展对策[J]. 海南大学学报(自然科学版), 2001,19(3):256-259.

[4] 韩 奇, 赵从举, 黄秋如. 1971-2011年海南气候变化特点及其对农业的影响——以海南省儋州市为例[J]. 天津农业科学, 2013,19(2):45-49.

[5] 王乙江, 彭世彰, 徐俊增,等. 神经网络方法计算参考作物腾发量精度分析[J]. 节水灌溉, 2012,(9):37-40.

[6] Droogers P, Allen R G. Estimating reference evapotranspiration under inaccurate data conditions[J]. Irrigation and Drainage Systems, 2002,16(1):33-45.

[7] Allen RG, Periera LS, Raes D, et al. Crop evapotranspiration: guideline for computing crop water requirement[Z]. FAO Irrigation and Drainage Paper 56, 1998.

[8] 高晓丽, 彭世彰, 徐俊增,等. 贵州省ET0计算方法的全局性评价及其率定[J]. 节水灌溉, 2014,(10):69-73.

[9] 刘战东, 刘祖贵, 秦安振,等. 黄淮海地区基于温度的ET0计算方法比较及修正[J]. 节水灌溉, 2014,(4):1-6.

[10] 王晓晨, 朱忠礼, 季 辰,等. 几种蒸散计算方法在怀来地区的适用性研究[J]. 气象, 2016,42(11):1 395-1 401.

[11] 郑 汐, 王 齐, 孙吉雄. 深圳地区参考作物蒸散量计算方法适用性分析[J]. 亚热带植物科学, 2010,39(4):28-32.

[12] Yang J, Liu C, Gao W. Comparison of the Hargreaves-Samani equation and the Priestley-Taylor equation for estimating reference crop evapotranspiration in the North China Plain[M]. Proceedings of SPIE - The International Society for Optical Engineering, 2014.

[13] 薛 璐, 牛文全, 张子卓,等. 简化参考作物蒸发蒸腾量公式在陕西关中地区的适用性研究[J]. 灌溉排水学报, 2015,34(6):62-67.

[14] 秦孟晟, 郝 璐, 施婷婷,等. 秦淮河流域五种参考作物蒸散量估算方法的比较及改进[J]. 中国农业气象, 2016,37(4):390-399.

[15] 谢 平, 陈晓宏, 刘丙军.湛江地区适宜参考作物蒸发蒸腾量计算模型分析[J]. 农业工程学报, 2008,24(5):6-9.

[16] Gunston H, Batchelor C H. A comparison of the Priestley-Taylor and Penman methods for estimating reference crop evapotranspiration in tropical countries [J]. Agricultural Water Management, 1983,6(1):65-77.

[17] 罗玉峰, 李 思, 彭世彰,等. 基于气温预报和HS公式的参考作物腾发量预报[J]. 排灌机械工程学报, 2013,31(11):33-36.

[18] Priestley C H B, Taylor R J. On the assessment of surface heat flux and evaporation using large-scale parameters [J]. Monthly Weather Review, 1972,100:81-92.

[19] Irmak S, Irmak A, Allen R G, et al. Solar and net radiation-based equations to estimate reference evapotranspiration in humid climates [J]. Journal of Irrigation & Drainage Engineering, 2003,129(5):336-347.

[20] Hargreaves GH, Allen RG. History and evaluation of Hargreaves evapotranspiration equation[J]. Journal of Irrigation & Drainage Engineering, 2003,129(1):53-63.