红壤涌泉灌水分入渗试验及数值模拟

赵新宇，吴荣清，梁欣欣，杨彦芬

(南昌工程学院，南昌 330099)

涌泉灌是采用加流量控制器的塑料细管作为灌水器与毛管相连接，并且可以与田间渗水沟辅助，以细流或射流局部湿润作物根区附近土壤，进行灌溉的一种灌溉方法[1]。涌泉灌解决了滴灌灌水器容易堵塞的问题，尤其适用于果树的灌溉，在水果产区应用很多。近年来国内外学者对涌泉灌技术进行了一些研究，如：吴端普进行了龙眼果树涌泉灌的效益分析[2]；谭明在我国西北干旱地区砂质土地上研究了果树涌泉灌的优缺点[3]；杨素哲进行了涌泉灌大田作物的试验研究[4]；蒋岑进行了干旱地区红枣树涌泉灌的技术研究[5]。但目前有关涌泉灌的理论研究还不多，本文通过室内试验与Hydrus-3D软件模拟，以南方红壤土为例，研究了在不同流量下涌泉灌的土壤水分运动规律，其成果可为灌水技术要素的制定提供理论支撑。

1 涌泉灌土壤入渗试验

1.1 供试土壤的物理性质

试验在鄱阳湖水工程安全与资源高效利用国家地方联合工程实验中心开展，试验红壤土样取自江西省进贤县。将试验土样风干、粉碎、过2 mm筛，用塑料薄膜覆盖保存备用。试验开始前测得土壤初始含水率为0.036，容重1.30 g/cm3土样的饱和导水率为2.141×10-5cm/s。使用BT-9300H(激光粒度仪)进行土壤颗粒分析，供试土壤的机械组成见表1。

采用高速离心机测定土壤水分特征曲线，使用定水头法测定土壤饱和导水率，运用VG模型(Van Genuchten)拟合土壤水分特征曲线见表2[6]。

表2 土壤的水力特性参数Tab.2 Hydraulic parameters of experiment soils

1.2 试验装置与方法

试验装置由马氏瓶、支架、玻璃转子流量计和透明玻璃土箱组成。采用量程为10～100 mL/min的玻璃转子液体流量计调节出水流量，调好流量后开始试验，土箱尺寸为 50 cm×50 cm×50 cm。试验装置如图1所示。

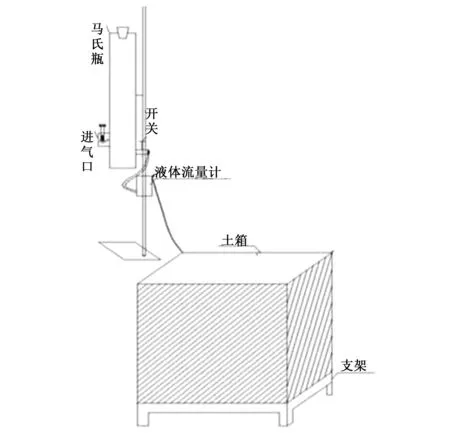
图1 涌泉灌试验装置示意图Fig.1 Experiment equipment for bubbled irrigation

在土壤密度相同，初始含水率相同的条件下，采用2、4、6 L/h等3个流量水平进行试验。实验开始前，用量筒校核出水口流量。试验开始后用秒表计时，记录下湿润锋在水平方向的扩散距离、垂直方向的入渗距离，并读取同时刻马氏瓶的刻度；由于水分入渗较快，逐一测量会存在延迟性造成误差，故先用笔在土箱侧面描绘处湿润锋的位置，待结束供水后在详细测量记录。 当供水流量为4、6 L/h时，会有积水出现。灌水结束10 min后，先用取表层5 cm土样，再用自制取土器按照图2所示位置分别取出土，然后烘干测定所取土壤的含水率。

图2 涌泉灌取样点分布图Fig.2 The schematic diagram of bubbled irrigation sampling points arrangement

2 土壤水分运动数学模型

2.1 土壤水分运动方程

基本假定：试验所用土壤是均质的且各项同性，空气、温度、土壤水分数量和能量关系的滞后对土壤水分运动的影响是忽略的。

涌泉灌水分入渗属于三维非饱和土壤水分运动。根据Darcy定律和质量守恒定律，土壤水分运动用理查兹方程描述[6]：

(1)

式中：θ为土壤体积含水率，cm3/cm3；t为时间，min；x、y、z为直角坐标，cm；K(θ)为土壤非饱和导水率，cm/min；ψm为基质势，cm。

2.2 定解条件

2.2.1 初始条件的设定

假定土壤初始含水率在计算区域内是分布均匀，求解土壤水分运动方程的初始条件是：

h(x,y,z,t)=h0(x,y,z)

(2)

0≤x≤X,0≤y≤Y,0≤z≤Z,t=0

式中：h0(x,y,z)为土壤初始负压力水头，cm。

参照实际试验情况来设定这一参数，同时假定土壤负压力水头均匀分布在计算区内，初始值设为-13 000 cm，相应实测初始含水率0.041 cm3/cm3。X、Y、Z分别对应于模拟区域横向、纵向及垂向坐标，相应的试验土箱，尺寸分别为：X=50 cm,Y=50 cm,Z=50 cm。

2.2.2 边界条件的设定

图3为模拟涌泉灌土壤水分运动计算区域示意图，坐标原点为出水口点O，对应室内试验，不考虑蒸散发及降雨强度，因此上边界OEFG为零通量边界。考虑地下水的埋深，下边界ABCD设置成第一类边界。边界OABG和边界OADE为出水口中心入渗面，由于对称性，为零通量边界。由于比较大的模拟计算区域，故可认为水分无法到达边界CDEF和BCFG，水通量为零，故也为零通量边界。边界条件可表示为：①边界OEFG处，不考虑降雨和蒸发强度时，q=0；②边界ABCD处：h(x,y,z,t)=h0，0≤x≤X，0≤y≤Y，z=-Z，t≥0；③边界CDEF处：h(x,y,z,t)=h0，0≤x≤X， -Z≤z≤0，y=Y，t≥0；④边界BCFG处：h(x,y,z,t)=h0，-Z≤z≤0，0≤y≤Y，x=X，t≥0；⑤边界OABG处：∂h/∂y=0，0≤x≤X，-Z≤z≤0，y=0，t≥0；⑥边界OADE处：∂h/∂x=0，-Z≤z≤0，0≤y≤Y，x=0，t≥0；⑦出水口O处：h=H(动水头边界)。

图3 计算区域Fig.3 Calculation area

2.2.3 数值求解方法

HYDRUS-3D[7]是由Simunek等人开发的有限元计算软件，可用于模拟土壤水流运动、溶质运移、热量传输与根系吸水等过程。采用HYDRUS-3D求解数学模型，数学模型的计算采用迦辽金有限单元法，利用隐式差分法[8]离散时间，迭代规则和容忍误差均按默认设置。采用三棱柱网格划分计算区域，网格大小设为1.50 cm，利用从密到疏的规律配置从上到下的网格。为了同试验结果做对比，同时验证湿润体内部土壤含水率，按照水平间距为5 cm，垂直间距为5 cm在计算区内设置16个观测点，如图4所示。

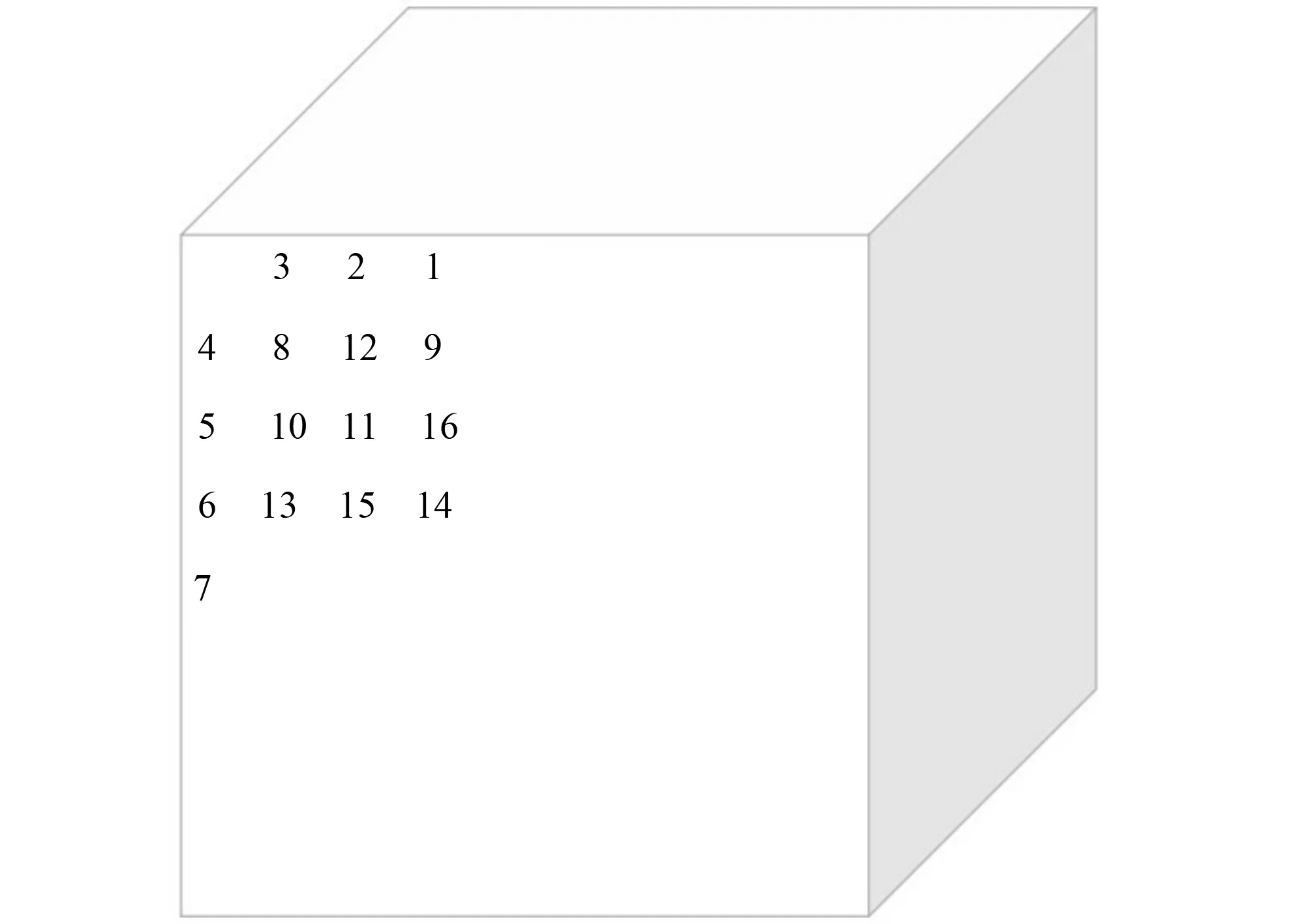
图4 观测点Fig.4 Observation points

3 模型验证

表3列出试验水平Q=2 L/h、Q=4 L/h、Q=6 L/h，T=8 h时，土壤含水率试验实测值和模拟值。可以看出，含水率的试验值和模拟值之间的相对误差在0.08%～13.60%之间，误差在距离出水口较远的地方较大。产生这些误差的主要原因可能是室内土箱装土时，人工夯土不均匀。仪器测量时引起的滞后效应也会产生误差。另外，土壤水势计算时，水分特性曲线转变成土壤含水量也造成一定的误差。总体而言，试验结果与模拟结果误差较小，两者较好的一致性，涌泉灌的土壤水分运动可用该模型来模拟。

表3 土壤实测含水率与模拟含水率的对比 %

4 不同流量条件下土壤水分运动的数值模拟

通过验证的HYDRUS-3D模型，可以对不同的土壤密度、初始含水率、流量等条件下的红壤涌泉灌水分入渗进行数值模拟，为渗泉灌灌水参数的制定提供理论支撑。本文进行了不同流量条件下的土壤水分入渗的数值模拟与分析。

4.1 流量对湿润体形状的影响

模拟灌水流量为Q=2 L/h、Q=4 L/h、Q=6 L/h，灌水时间为T=2 h、T=4 h、T=8 h时湿润体土壤含水量如图5所示。不同流量条件下，随着流量的增大，湿润体形状相应变大；随着时间的推移，入渗的水平半径、入渗的竖直深度渐渐变大；但随时间的增加，入渗的幅度渐渐减小，即湿润体扩散速率在水平和竖直方向不断减小。相同流量下，同一时间内土壤水分向下入渗距离比水平扩散距离大，湿润锋竖直比水平运移距离大，湿润体近似椭球体。随着流量变大，湿润锋在竖直与水平方向的移动距离差异变大，湿润体更趋于扁平。

图5 涌泉灌土壤剖面体积含水率分布Fig.5 Bubble Irrigation volumetric water content in soil profile distribution

随着灌水时间的延长，灌水量不断增多，湿润体逐步扩大，湿润的轮廓线不断向外延伸，但推进的速度的变慢。湿润体内的高含水区的含水量接近饱和值，流量越大，高含水区的范围就越大。这是因为土壤入渗能力小于供水强度，经过一段时间的灌水，出水口土壤表层产生积水，这样就造成在积水区域周围的土壤含水率快速达到饱和状态，促进水平方向的扩散；在重力势能和基质势能的作用下，随着土壤水势梯度递减，土壤水在垂直方向的运动增大，所以随着流量的变大湿润体内高含水区的范围也相应变大。

4.2 流量对土壤含水率的影响

以A点(0，0，-10)和B点(-10，0，-10)为例，分析土壤含水率在不同流量下的变化情况，两点的含水率变化曲线如图6所示。

图6 流量对土壤体积含水率的影响模拟Fig.6 Simulation of the effect of flow on soil moisture content

在位置不同的A、B两点，当湿润锋到达时，含水量迅速增加，随着灌水的时间逐渐增大，变化趋势趋于平缓，最后接近于稳定，这说明随着流量的增加，土壤水分运动特征值也随之变大，变化幅度随着时间的增加而减小。B点至入渗点O的距离较大，在入渗开始阶段，A点的土壤含水量上升较快，随着时间的增长，两点的土壤含水量趋近于相同，当流量为Q=6 L/h时，土壤含水率接近于饱和。

当流量不相同时，流量越大，湿润锋经过A、B两点所需时间越少；流量越大，土壤含水率增加的速率越快；土壤含水率随流量的增大而增大。随着时间的推移，不同入渗流量的三条土壤含水量曲线接近于平行，说明当入渗稳定后，土壤含量与入渗流量呈等比例增加的关系。另外，在距离出水口同一距离，随着土壤在竖直方向的深度增加，湿润体内的含水率渐渐变小；同一土壤深度，距离出水口距离越大，湿润体内含水率越小。

5 结 语

通过不同流量的红壤涌泉灌水分入渗实验与HYDRUS-3D数值模拟，研究了涌泉灌土壤水分运动，研究结果表明：

(1)涌泉灌室内入渗实验与HYDRUS-3D数值模拟的土壤含水率相对误差在0.08%～13.60%之间，两者具有较好的一致性，该模型能比较好地反映涌泉灌的三维土壤水分入渗运动，可以用于红壤涌泉灌水分运动的模拟。

(2)数值模拟说明：土壤水分入渗湿润体的形状接近于椭圆形，湿润体的大小、湿润体内高含水区域的大小随入渗流量的增大而增大；随着土壤竖直深度、水平距离的增大，湿润体内的含水率渐渐变小；随着流量的增加，土壤水分运动特征值增大，变化幅度随时间的增加而减小；入流量越大，湿润锋运移速度越快，土壤含水率增加的速率越大；当入渗稳定后，土壤含水量与入渗流量呈等比例增加的关系。

[1] 杨素哲，沈菊艳，黄宝全，等. 果树涌泉灌溉方式的技术应用[J]. 农业工程学报，2005，21，(S1):68-71.

[2] 吴端普，洪波涛，李晓瑜，等. 龙眼需水量及微喷灌增产效益分析[J].中国农村水利水电，2002，(3):28-30.

[3] 谭 明. 涌泉灌技术应用[J].节水灌溉，2003，(6):24-26.

[4] 杨素哲，陈玉民，黄宝全. 涌泉灌技术在大田作物灌溉中的试验研究[J].节水灌溉，2005，(3):32-34.

[5] 蒋 岑，谢香文，王长新，等. 模糊数学在干旱区成龄枣树微灌技术选择中的应用[J].节水灌溉，2010，(1):9-11.

[6] 李春友，任 理，李保国.利用优化方法求算Van Genuchten方程参数[J].水科学进展，2001，12(4):473-477.

[8] Lubana P P S, Narda N K.Soil water dynamics model for trickle irrigated tomatoes[J]. Agricultural Water Management,1998,37(2):145-161.