水分特征曲线Gardner模型参数的预测模型对比分析

李浩然，樊贵盛

(太原理工大学水利科学与工程学院，太原 030024)

土壤水分特征曲线是描述土壤基质势与土壤含水量之间关系的基本曲线[1]，可以反映出土壤孔隙结构特点与持水能力，对于研究土壤水分动态、溶质运移等有着重要的意义。在对土壤水分特征曲线的研究中，许多学者提出了不同的物理—经验模型用来对土壤水分特征曲线进行描述。目前，常见的经验模型有V-G模型、Gardner模型、F-X模型等，其中Gardner模型由于其简单的结构形式、少量的参数以及较高的精确性等优点，受到众多学者的认同。宋孝玉等[2]通过部分不同区域土壤进行了Gardner模型建立与比较，证明了Gardner模型的准确性与适用性；张露[3]等利用Gardner模型成功拟合出不同复配土壤的土壤水分特征曲线；李逸[4]等利用Gardner模型进行拟合，得出了土壤水分特征曲线的斜率主要由土壤质地决定的结论等。

而在土壤水分特征曲线的研究中，如何准确地获取模型中的参数一直是人们研究的重点。对于模型参数的获取一般有直接法(负压计法、压力膜仪法、砂形漏斗法)与间接法。由于直接方法在对参数的测定中需要耗费较多的人力物力，同时测量的结果易受外界条件的影响，从而导致精度较差。目前，随着土壤传输理论的发展，运用土壤传输函数对土壤特征参数进行预测的间接方法成为了人们研究的焦点。李晓鹏等[5]使用多种不同的土壤传输函数，对不同地区土壤的饱和含水率进行了预测，并成功得出适合各地区饱和含水率的饱和含水率；舒凯民[6]等利用BP神经网络对入渗参数进行预测，并取得了较好的效果；Vereecken[7]运用线性回归分析对土壤水分特征曲线参数进行了研究，即对模型参数进行了线性函数的预测。

根据以上研究可以看出，土壤传输函数可以有效地对土壤的特征参数与运动参数进行推求与预测。但是，对于土壤水分特征曲线Gardner模型参数的研究还鲜有报道。目前，在土壤传输函数的方法中，BP人工神经网络与支持向量机(SVM)是运用相对广泛、精度较高的两种方法。因此，本研究将在不同输入变量的条件下，利用BP神经网络与支持向量机两种预测手段对Gardner模型参数进行预测，并对预测模型的精度进行分析，为土壤水分特征曲线Gardner模型参数的预报模型的创建提供依据和参考。

1 材料与方法

1.1 试验区土壤条件

试验所用土样均来自山西省中西部地区的耕作农田。试验区地貌条件为平原、丘陵和高原等，气候属于典型的温带大陆性气候。土壤类型有黄褐土、棕壤土等；土壤质地类型复杂多样，主要包括粉砂质壤土、砂质壤土等。试验区土壤基本理化参数变化范围如表1所示。

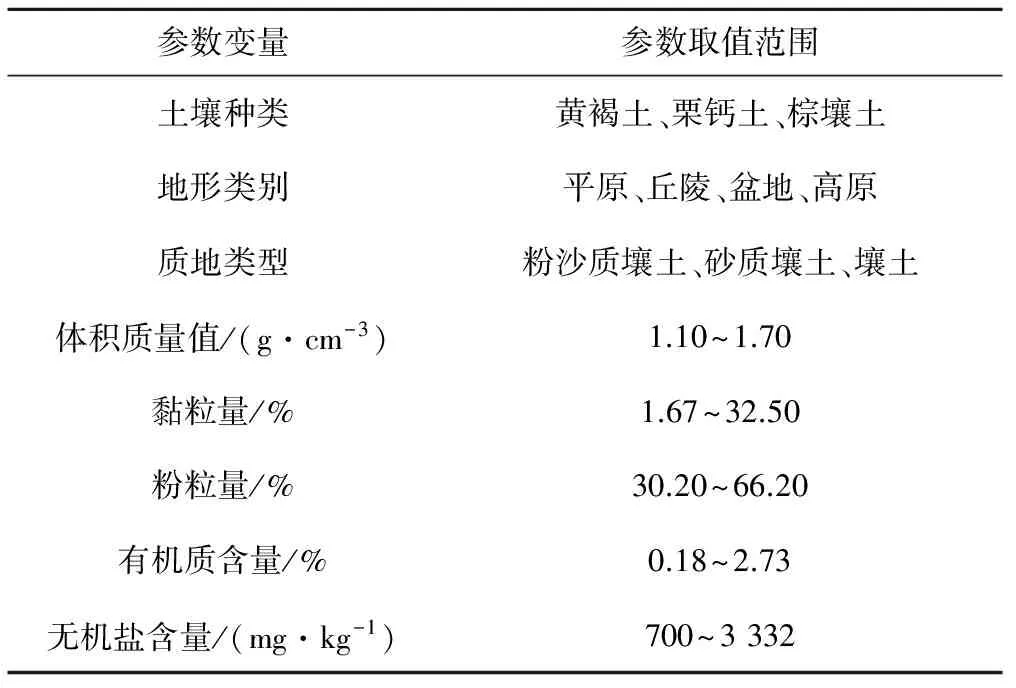
表1 土壤样本数据的取值范围

1.2 试验设备与方法

本文土壤水分特征曲线试验使用1500F压力膜仪进行。首先将土样风干、过筛，并将其装入相应的环刀内，然后将环刀放入仪器中的陶土板中令其吸水以保证土样达到水分饱和。当土样达到水分饱和后，对土样进行固定压力值的施压，以保证土壤中的水分可以充分排出，并间隔固定时间对土样进行称重。当前后称重的土样重量变化小于0.005 g，则认为土样中的水分全部排出，开始进行下一压力值的试验。最后计算含水率，并通过相应的计算拟合得到Gardner模型参数值。

本次试验需要测定的土壤基本理化参数主要包括土壤容重、土壤质地、有机质含量、无机盐含量。其中由于是土样为扰动图，土样容重按照1.10～1.70 g/cm3进行配置；土壤质地通过激光粒度分析仪对土壤中的黏粒、砂粒、粉粒含量进行测定；土壤有机质含量使用重铬酸钾容量法测定；土壤无机盐含量是通过火焰光度计等仪器对八大离子进行测定，并将测定值累加，和值为无机盐含量。

1.3 Gardner模型

Gardner模型是Gardner在1970年提出[8,9]，因其结构简单、精度及较高而广泛应用于实际当中。 Gardner模型的具体表达式为：

h=aθ-b

(1)

式中：h为土壤水吸力，cm；θ为土壤体积含水率，%；a、b均为拟合参数，无单位量纲且均为正数。

1.4 数据样本

通过实验，建立了100组数据的样本，即建立了土壤基本理化参数与Gardner模型参数a、b的一一对应关系，代表性数据样本见表2。

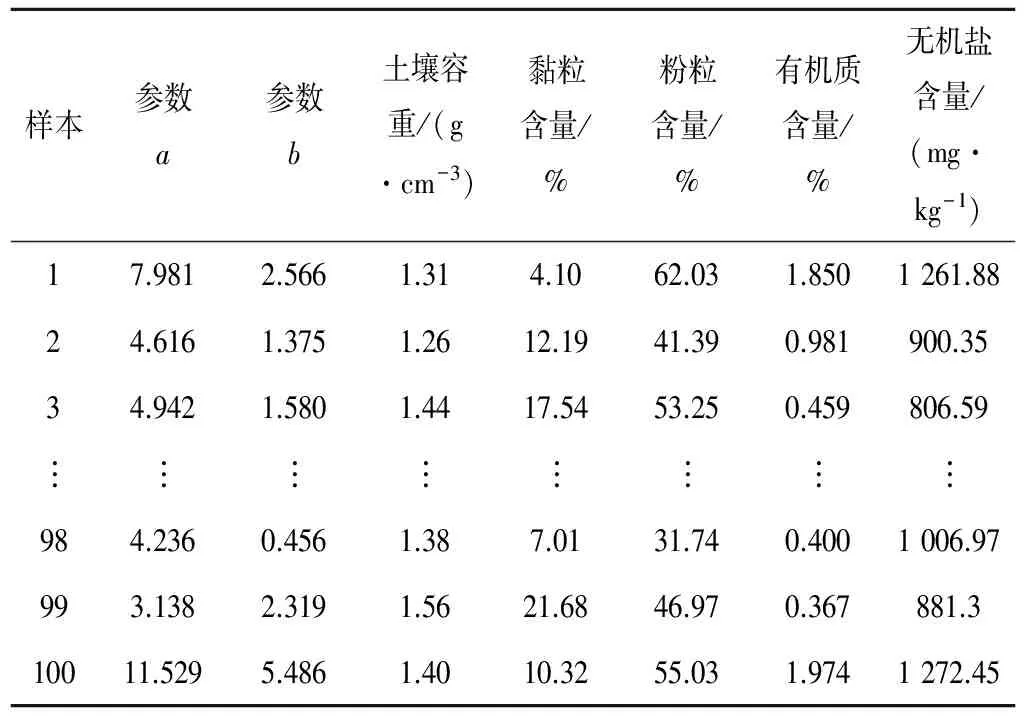
表2 建模样本数据表

2 输入变量情景设计与预测模型的建立

2.1 土壤水分特征曲线主导因素分析

土壤水分特征曲线的过程线决定着Gardner模型的参数，而影响土壤持水性能的土壤基本理化参数的较多。前人[10,11]和本文的分析认为主要的影响因子有土壤质地、土壤容重、土壤有机质含量、土壤无机盐含量等。

(1)土壤质地。土壤质地主要是指土壤中黏粒、粉粒、砂粒的组成情况。对于土壤而言，如果土壤中的黏粒含量与粉粒含量越高，土壤中会形成较多的中小空隙，进而导致土壤中的毛管吸力增大，使得土壤的持水性能增加；另一方面，中小孔隙的增加会增加土壤的比表面积，表面能变大，从而导致土壤颗粒对水分的吸附能力变强。

(2)土壤容重。土壤容重表示的是土壤结构的密实程度与板结程度。对于多孔隙的土壤而言，土壤容重的增大代表着土壤被压缩破坏，土壤中的大孔隙被挤压破坏形成中小孔隙，从而导致土壤的毛管吸力与土体颗粒对水分的吸附能力变强。

(3)土壤有机质含量。土壤中的有机质主要是指土壤内的胶结物质，这些物质会增大土壤的黏性从而改变土壤的内部结构。在有机质的作用下，土壤内的中小孔隙的结构变得比较稳定，因此有着较强的持水稳定性。

(4)土壤无机盐含量。土壤中的无机盐含量主要是指土壤中的八大离子的含量总和，随着土壤中的含盐量的增加，土壤分散度变大，土壤中的大孔隙崩塌，从而形成较多的中小孔隙，从而加强土壤的持水性能。

2.2 输入变量情景设计

为了探究输入变量对于BP神经网络与支持向量机预报模型预测精度的影响，需要对输入变量的选择方面设计了不同的情景模式。

输入变量的情景设计主要以输入变量的数量和类型为原则。根据查阅文献与机理分析，认为土壤持水能力与土壤质地与土壤容重有着直接的关系，因此在设计输入变量的时候，土壤质地与土壤容重是不可或缺的变量；同时，还应考虑到土壤有机质含量与土壤无机盐含量对土壤持水性能的作用，以及输入变量数量的改变对Gardner模型参数预测精度的影响。

将以上因素综合考虑，最终确定的输入变量情景为3种模式，分别为：①土壤质地+土壤容重；②土壤质地+土壤容重+土壤有机质含量；③土壤质地+土壤容重+土壤有机质含量+土壤无机盐含量。

2.3 土壤传输函数预报模型

(1)支持向量机是Corinna Cortes和Vapnik等于1995年首先提出的一种处理小数据、非线性等问题的机器学习方法。支持向量机通过特定的映射，将因变量投影到高纬度的运算空间当中，借助于核函数展开计算，从而解决样本空间的非线性分类与回归分析的问题。支持向量机由于能有效避免预测过程中的“过学习”、“过拟合”等问题，因此在近些年受到广大学者的关注研究。具体预测模型如下：

model=svmstrain(train_Y,train_X, ‘options’)

(2)

式中：svmtrain为向量机训练形式；train_X为自变量训练集属性矩阵，包括输入变量；train_Y为因变量训练集标签，包括Gardner模型参数；options为参数选项，依据核函数类型，主要包括C、ε、σ，其中，C为惩罚因子；ε为不敏感损失函数值；σ为核函数参数。式(2)为支持向量机模型。

(2)BP神经网络是1986年由Rumelhart和McClelland提出的一种按照误差逆向传播算法训练的多层前馈神经网络。BP神经网络因其自身特有的对于非线性关系处理能力与相对简单的组成结构，在众多人工神经网络中研究最为成熟，是目前应用最广泛的神经网络。具体预测模型如下：

net=newff( min max(traininput),[20,2],{‘tan sig’,‘purelin’},‘trainlm’)

(3)

式中：net为本文所创建的BP神经网络模型；newff为在Matlab程序中的BP神经网络函数；min max( ) 为决定输入参数取值范围的向量矩阵；20和2为分别为隐含层和输出层神经元的个数；{‘tan sig’,‘purelin’}分别为隐含层和输出层的传输函数形式；‘trainlm’ 为训练函数形式。式(3)为BP网络模型。

2.4 预报模参数与成果

2.4.1 样本数据预处理

为了方便预报模型的计算以及减少输入因素量纲对预测精度的影响，因此对输入变量的数据进行归一化处理，归一化处理公式如下。

(4)

式中：Y为归一化处理后的数据；X为样本数据；Xmin、Xmax分别为样本数据的最大值与最小值。

2.4.2 BP模型结构与相关参数

(1)BP神经网络的结构主要分为输入层、隐含层、输出层。通过对样本不停地学习与训练，以均方误差最小化作为反馈结果，进而修正调整网络权值和阈值，最终高度拟合数据并得出结果。BP神经网络结构如图1所示。

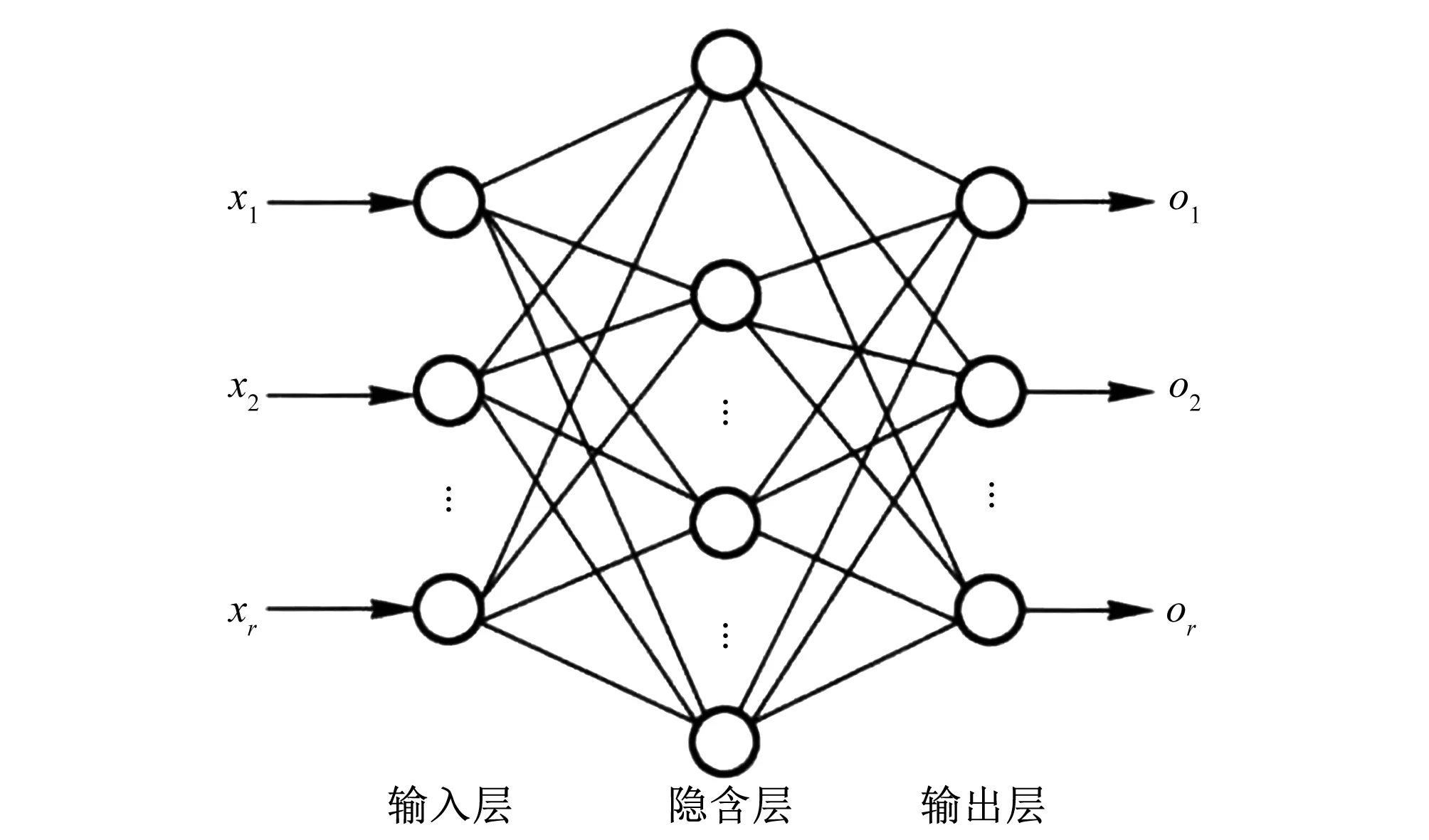
图1 BP神经网络结构图

(2)BP相关参数。本文所用BP神经网络预报模型的参数设定为最大学习迭代次数为1 500次，学习率0.01，训练精度为0.000 5。最终确定的参数如表3所示。

2.4.3 SVM模型相关参数

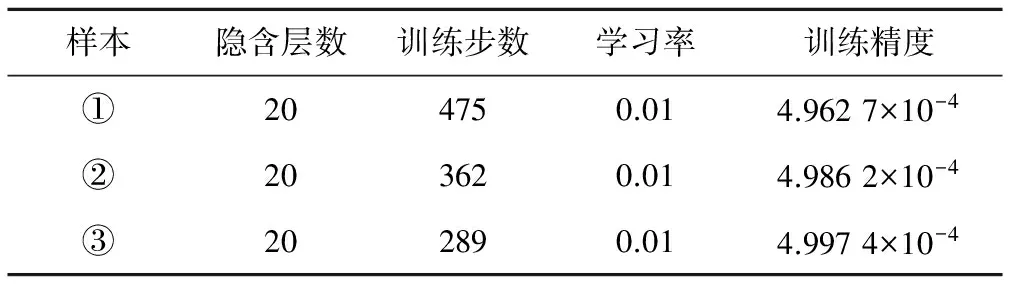
表3 BP神经网络预报模型参数

(1)SVM结构。支持向量机是将输入变量映射到高维空间中，在高维空间中寻找一个最优分类超平面，保证训练样本中不同分属的点可以很好地分布在超平面的不同侧面，从而使空白区域实现最大化，同时此超平面即为支持向量机的结果。支持向量机结构如图2所示。

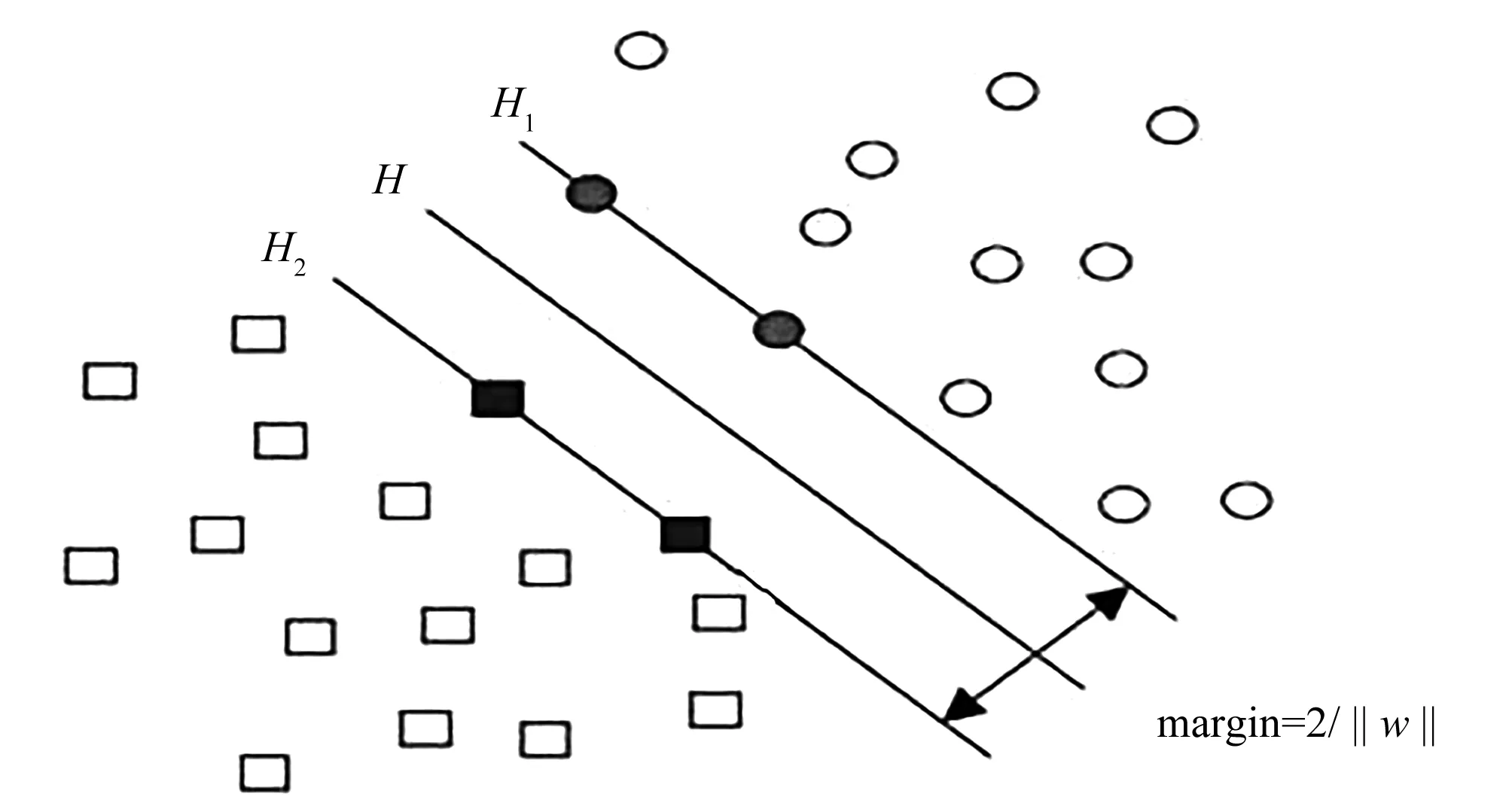
图2 SVM最优超平面示意图

(2)SVM相关参数。本文所用支持向量机预报模型的相关参数主要有C、σ、ε，其中C为惩罚因子，ε为不敏感损失函数值，σ为核函数参数。最终确定的参数如表4所示。

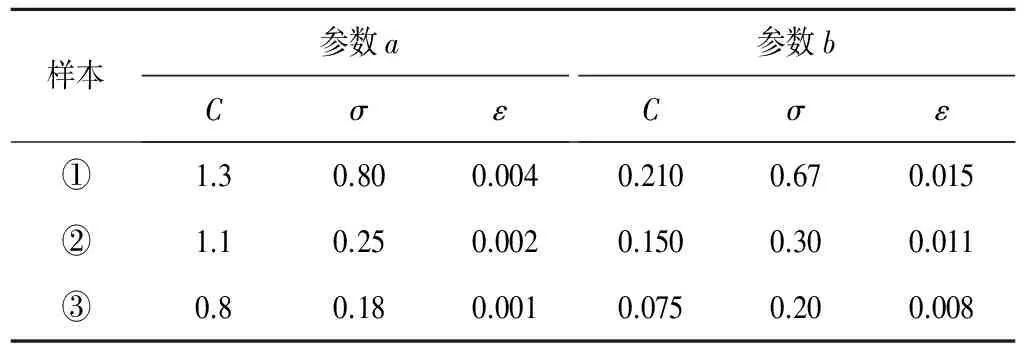
表4 SVM预报模型参数

3 预报模型精度比较

将归一化处理后的样本数据按分别通过支持向量机与BP神经网络的预报模型的预测，并将预测值与实测值进行比较。预测结果的精度比较如表5所示。

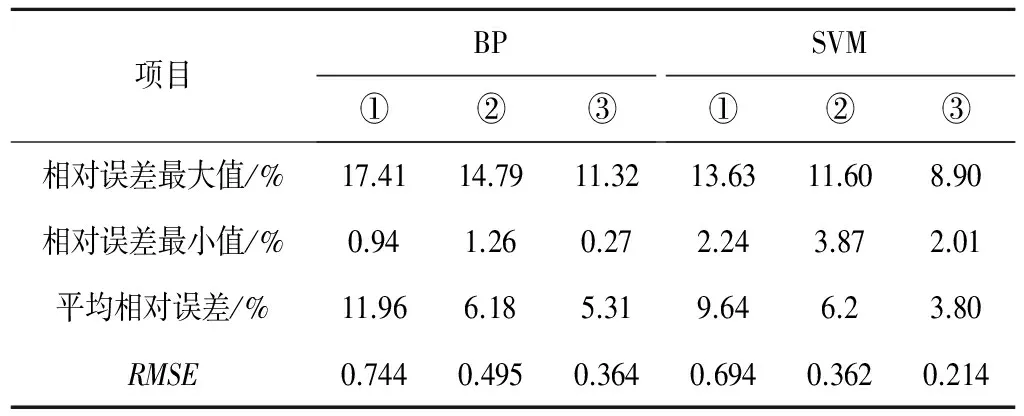
表5 参数a预测误差结果表

注：RMSE为均方根误差。

由表5可知，当输入变量只有土壤质地与土壤容重时，两种模型的平均相对误差分别为11.96%与9.64%，相对误差较大，精度较低；但是随着输入变量种类的增加，无论是BP神经网络预报模型模型还是支持向量机预报模型，对于参数a预测的相对误差值呈现出逐渐下降的趋势，模型的预测精度不断提高，并在输入变量为土壤质地、土壤容重、土壤有机质含量、土壤无机盐含量时，平均相对误差达到最小值，分别为5.31%与3.80%，预测精度较好。这不仅说明输入因子的种类变化对Gardner模型参数的预测精度的影响程度较为明显，同时证明了两种预测模型可以实现对于Gardner模型参数a的预测。

将两个预报模型进行对比，两者的误差相差较小，精度相似。随着输入变量的增加，BP神经网络的相对误差最大值分别为17.41%、14.79%、11.32%，最小值分别为0.94%、1.26%、0.27%；支持向量机的相对误差最大值分别为13.63%、11.6%、8.9%，最小值为2.24%、3.87%、2.01%。可以看出，虽然BP神经网络的最小相对误差值比支持向量机要小，但是就相对误差波动的范围而言，支持向量机的预测结果的波动程度较低，变化幅度较小；另一方面，RMSE是一种反映预测值与实测值之间偏差程度的数学手段，RMSE越小则实测值与预测值之间的离散程度越小，从表5可以看出，无论输入变量的种类有多少，支持向量机对于参数a的RMSE都比BP神经网络小，从而进一步说明支持向量机的预测结果的相对稳定，能够有效的保证预测结果的精度。

如表6所示，与参数a的预测结果相似，无论是BP神经网络还是支持向量机，预测精度均会随着输入变量的增加而提高，最终平均相对误差分别为5.56%与3.76%，预测精度较高，说明了土壤基本理化参数的变化对预测的效果有着明显的影响。而且将两种模型进行对比，BP神经网络预测误差的最大值为19.04%、13.79%、10.58%，最小值为1.07%、0.627%、0.651%；支持向量机预测误差最大值为16.86%、12.56%、7.86%，最小值为3.21%、2.16%、1.27%。同参数a的结果相似，虽然BP神经网络的最小相对误差值比支持向量机的要小，但是支持向量机预测的相对误差区间相对较小，同时根据RMSE的数值可以看出支持向量机对于参数b的预测结果的离散程度较低，吻合度相对较高。

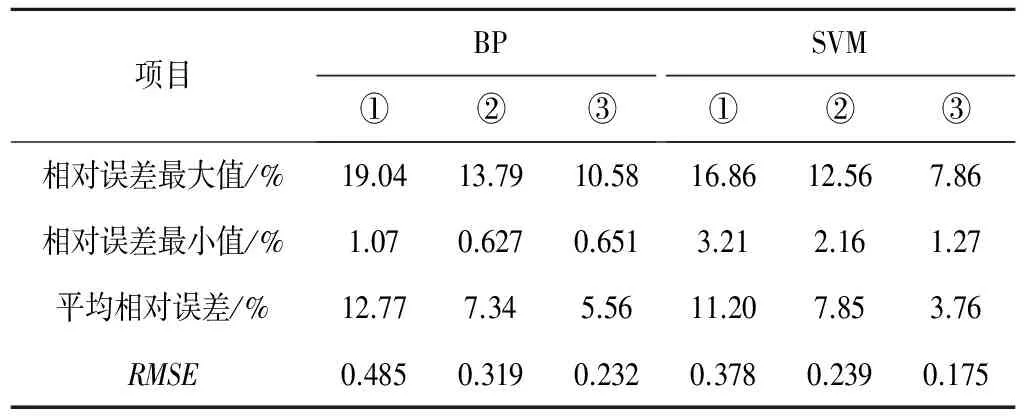
表6 参数b预测误差结果表

综上所述，对于Gardner模型而言，改变输入因子的类型与数量可以有效地提高预测的精度，并且能够有效的对Gardner模型参数进行有效的预测。同时，采用支持向量机算法对Gardner模型参数进行预测，所得到的结果相对稳定，吻合度较好，使得相对误差保持在较小的范围内，相比于BP神经网络的波动性，支持向量机能够使预测结果保持较好的稳定性。

4 结 语

(1)在土壤特征曲线主要影响因素范围内，两种预报模型的预报精度随着输入因子类型的增加而提高，并在输入变量为土壤质地、土壤容重、土壤有机质含量、土壤无机盐含量时精度达到最高，预测结果的平均相对误差均在6%以下。以土壤质地、容重、有机质含量、无机盐含量为输入变量的BP神经网络与支持向量机预报模型都可用于Gardner模型参数的预测。

(2)BP神经网络预报模型的预测误差的最小值小于支持向量机的最小值，但是支持向量机预报模型预测结果的波动较小，RMSE较低，预测结果吻合度较高，支持向量机预报模型相对于BP神经网络模型有着更好的稳定性准确性。

(3)本文研究了BP神经网络与支持向量机预报模型的预测结果，证明了支持向量机对于Gardner模型参数的预测有着更高的精确度。此次研究为土壤水分特征曲线参数预测方法的选择提供了理论依据。在今后的实验中，会尝试不同的预测方法，比如灰色预测模型、BNN预测模型等，对Gardner模型参数进行预测以及对比分析，进一步丰富土壤传输函数理论。

[1] 雷志栋，杨诗秀，谢传森.土壤水动力学[M].北京：清华大学出版社，1988．

[2] 宋孝玉, 李亚娟, 李怀有,等. 土壤水分特征曲线单一参数模型的建立及应用[J]. 农业工程学报, 2008,24(12):12-15.

[3] 张 露, 韩霁昌, 罗林涛,等. 砒砂岩与风沙土复配土壤的持水特性研究[J]. 西北农林科技大学学报(自然科学版), 2014,42(2):207-214.

[4] 李 逸, 金建新. 石羊河流域下游地区土壤水分特征曲线研究[J]. 节水灌溉, 2014,(7):10-11.

[5] 李晓鹏, 张佳宝, 吉丽青,等. 土壤传递函数在计算土壤饱和导水率中的应用[J]. 灌溉排水学报, 2009,28(2):70-73.

[6] 舒凯民, 樊贵盛. 基于Kostiakov二参数入渗模型参数的BP预测[J]. 节水灌溉, 2016,(10):1-5.

[7] Vereecken H J, Maes J, Feyen J, et al. Estimating the soil moisture retention characteristic from texture, bulk density, and carbon content[J]. Soil Science, 1989,148(6):389-403.

[8] Gardner W R，Hillel D，Benyamini Y. Post-irrigation movement of soil water:I. Redistribution[J]. Water Resources Research，1970，6(3):851-861.

[9] Gardner W R，Hillel D，Benyamini Y. Post-irrigation movement of soil water:P. Simulations Redistribution and evaporation[J]. Water Resources Rrsearch，1970，6(4):1 114-1 153.

[10] 苏 杨, 朱 健, 王 平,等. 土壤持水能力研究进展[J]. 中国农学通报, 2013, 29(14):140-145.

[11] 冯永军, 聂俊华, 张 红. 土壤持水性能及影响因素[J]. 山东农业大学学报(自然科学版), 1996,(3):298-302.