基于CFD的映秀湾电站过流部件的分析
2018-03-21张富成
卿 彪,杨 军,唐 军,张富成
(国网四川省电力公司映秀湾水力发电总厂,四川 都江堰 611830)
0 引 言
映秀湾电站在经过多年运行之后,尤其是在经过地震和泥石流灾害之后,映秀湾电站水轮机机组的效率和稳定性都降低,空化空蚀现象特别严重,严重影响了机组稳定和高效运行。因此,为了提高机组的性能,从而确保机组稳定,高效的运行,有必要对映秀湾电站的水轮机组进行改造。在对映秀湾电站水轮机的转轮进行优化分析之后,选择了一个适合于映秀湾电站的高效的转轮A606c。
为了确定新选择的转轮是否符合映秀湾电站水轮机组的尺寸,以及运行中对水流流态的影响,就有完全必要对映秀湾电站原有的过流部件进行分析,从而确定新选择的转轮与过流部件在尺寸上是否匹配,从而找出原过流部件是否有需要进行修型的部位,
从而确保机组的振动和摆度合理,转轮与过流部件的空化性能良好。进而达到映秀湾电站水轮机改造的目的,提高整个机组的运行效率。
映秀湾电站的过流部件主要有蜗壳,固定导叶,以及活动导叶,这些部件都是埋设部件,因此此次分析采用的手段只能是数值模拟,也就是利用计算流体动力学(CFD)。故而此次计算分析主要集中在蜗壳,固定导叶,活动导叶。如表1所示为原水轮机设计参数。
1 控制方程
为了使得此次计算更加的合理,本次计算先对蜗壳和固定导叶进行计算,而后对固定导叶和活动导叶进行联合计算。在计算过程当中涉及的基本控制方程如下[1-3]:
连续方程:
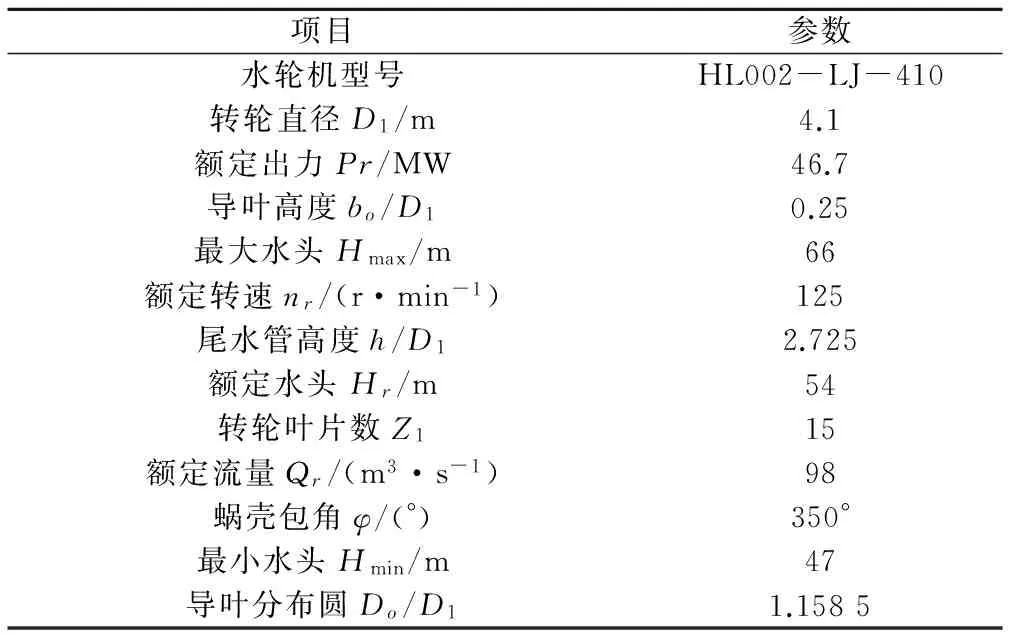
表1 原水轮机设计参数Tab.1 Design parameters of raw water turbine
(1)
动量方程:
(2)
RNGk-ε模型:1986年Yakhot和Orszag提出RNGk-ε模型。Renormalization Group(译为重正化群)的缩写为RNG。修正后的k方程和ε方程形式分别如下:
式中:μt=ρCμκ2/ε为湍流黏度;μeff=μ+μt为有效黏性系数;μt分析了旋转叶轮式流体机械流场效果。
2 CFD计算
2.1 蜗壳与固定导叶的CFD计算
蜗壳是水流进入水轮机的第一个部件,同时它将水流引向导水机构并进入转轮区,因此在电站的改造后应当尽量减少水流在蜗壳当中的水力损失,同时保证水流能够均匀、轴对称地进入蜗壳,提高机组运行的稳定性[4]。映秀湾水电站在重新选择了新转轮之后,新转轮的尺寸和旧转轮的尺寸有一定的差异,因此有必要对现有的蜗壳和固定导叶进行优化分析,而用数值方法研究蜗壳内部流场已经成为改进和优化蜗壳与固定导叶设计的一个重要的手段[5]。
利用三维建模软件UG对映秀湾电站蜗壳进行三维建模[6],ICEM进行网格划分,如图1所示,将划分好的网格导入CFX软件当中进行计算,此次计算工况取Q11=650 L/s(最优工况附近单位流量)和Q11=750 L/s(额定工况附近单位流量),额定工况下蜗壳的计算结果如图1-4所示。

图1 蜗壳三维实体图Fig.1 Three dimensional solid diagram of the spiral case
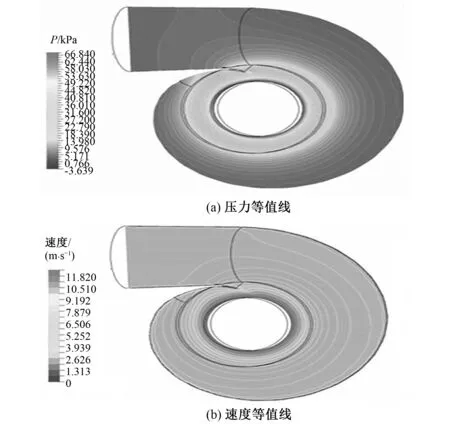
图2 蜗壳压力及速度等值线Fig.2 Spiral case pressure and velocity contour
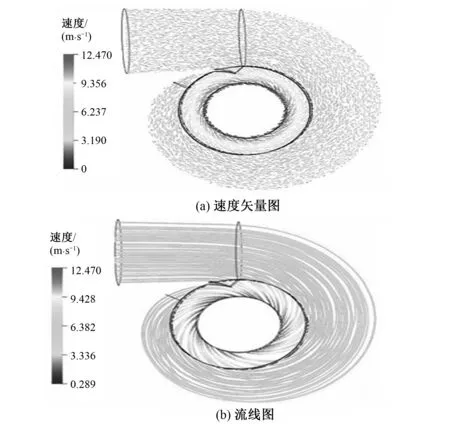
图3 蜗壳速度矢量和流线图Fig.3 Velocity vector and streamline of spiral case

图4 蜗壳断面速度矢量图Fig.4 Velocity vector of the section of the spiral case
根据流场计算结果计算了蜗壳内直径为558.3 mm(模型尺寸D1=350 mm)圆周(固定导叶外切圆)上的出流角。蜗壳出流角与固定导叶进口安放角比较,见图5所示。从图中分析可知,在整个蜗壳包角范围内,蜗壳出流角变化从 23.1~31°左右,角度变化范围在8°左右。同时蜗壳内流态分布也显示出蜗壳压力分布、流线均匀合理。 因此映秀湾电站蜗壳 CFD 计算结果是比较理想的。从图5来看,固定导叶进口安放角约为 27°,与蜗壳的匹配也基本合适。图6为固定导叶头部进口区域速度矢量分布图,从图中也可以得出,固定导叶进口区域内的流线分布也是比较均匀合理的。
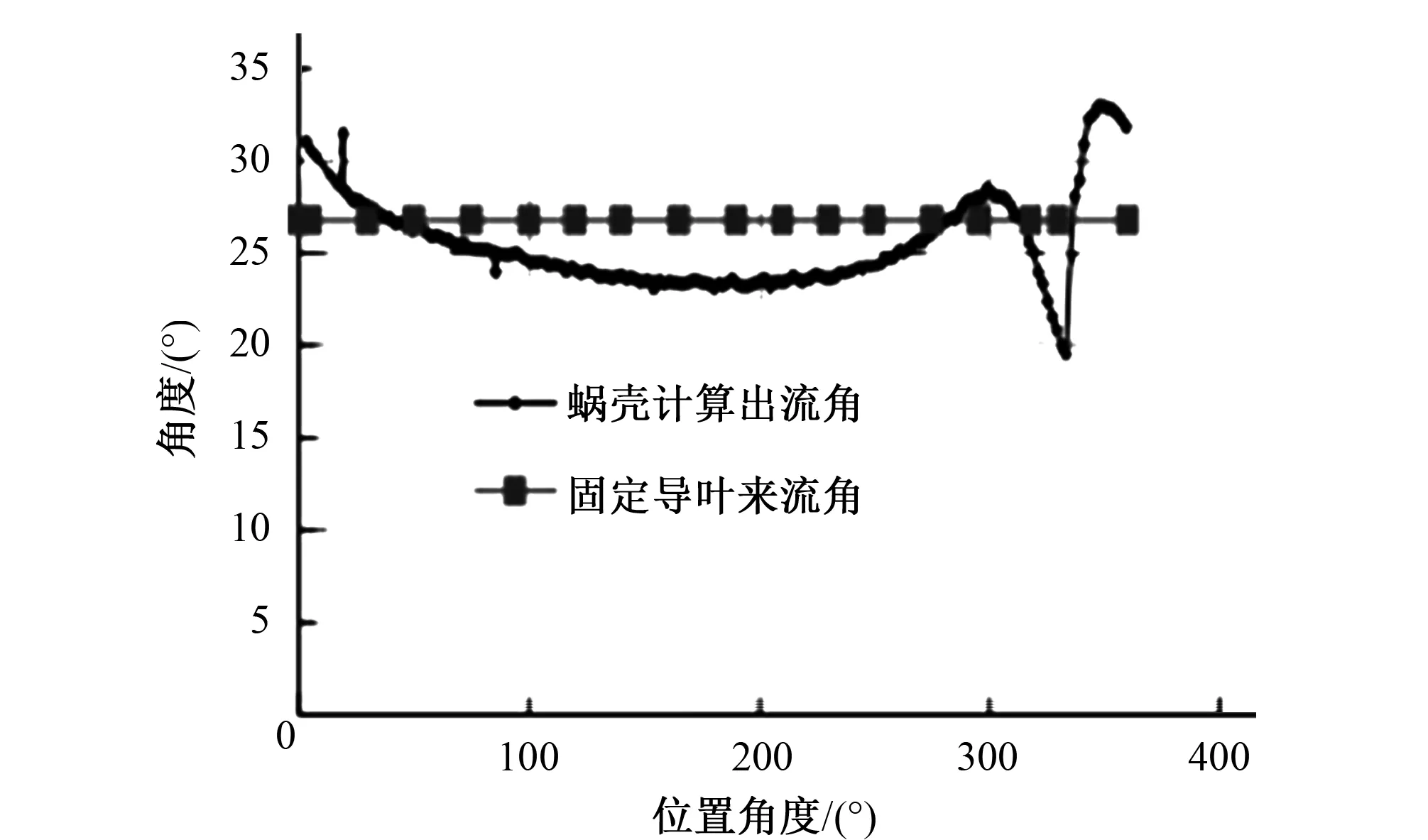
图5 蜗壳出流角与固定导叶进口安放角的比较Fig.5 Comparison between the outlet angle of spiral case and the inlet angle of fixed guide vanes
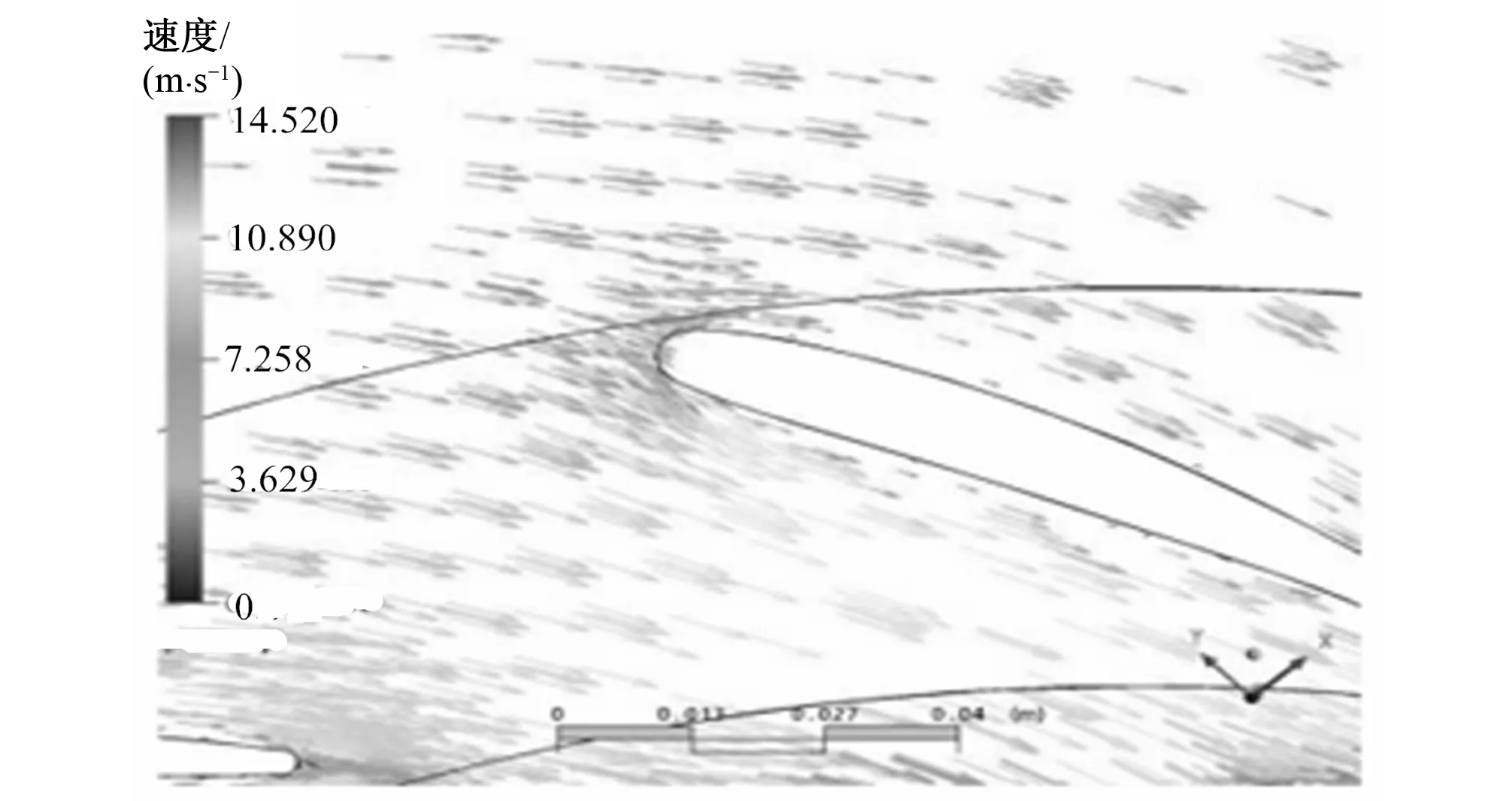
图6 固定导叶头部进口区域速度矢量分布Fig.6 Fixed guide vane head inlet region velocity vector distribution
2.2 固定导叶与活动导叶的CFD计算
在转轮与活动导叶的联合计算分析中,计算了转轮最优效率与开口的对应关系,从中可知,转轮A606c与正曲率导叶相配时,最优开口为16 mm(模型转轮对应的开口值)。
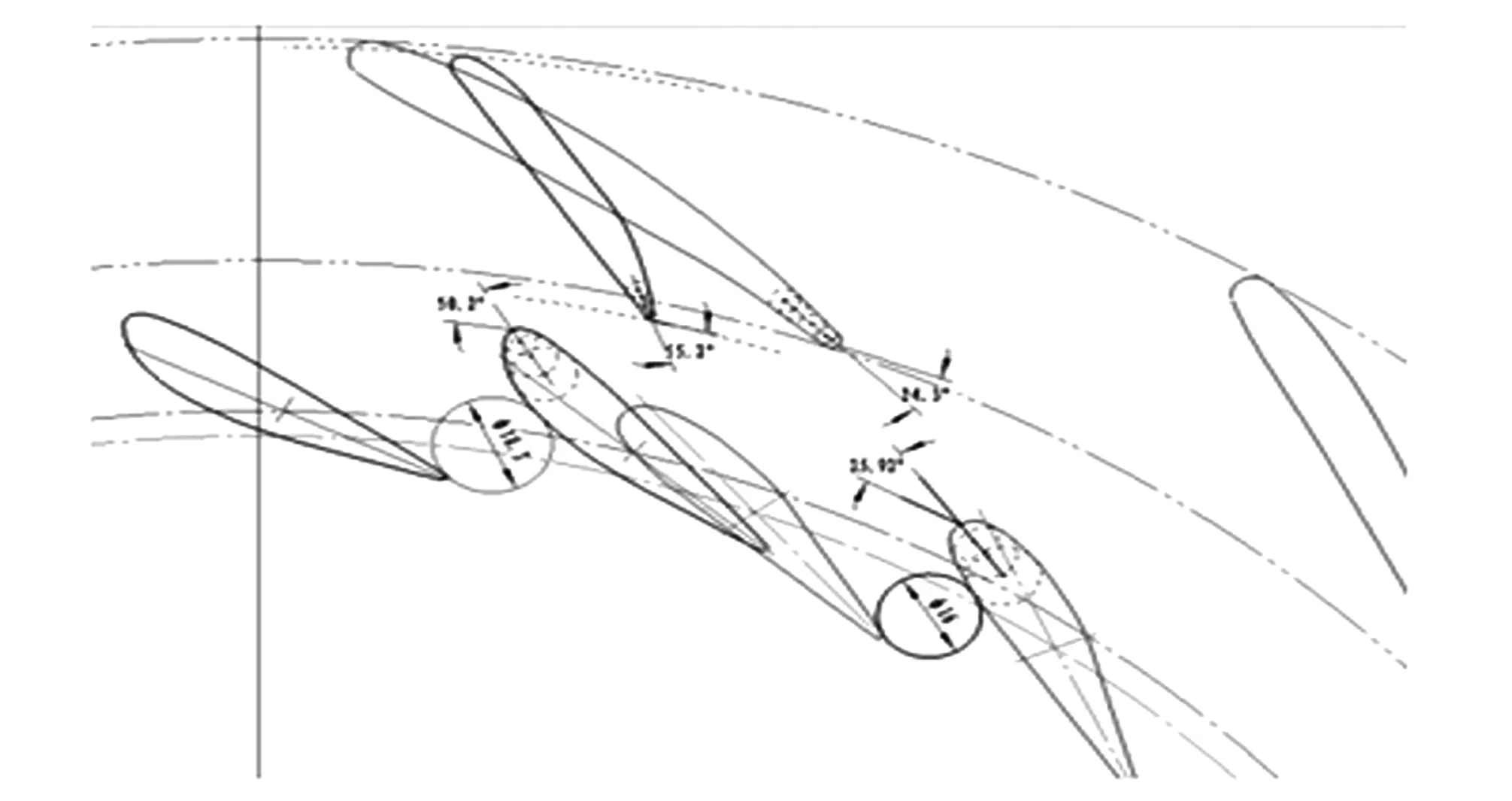
图7 活动导叶最优开口与固定导叶几何关系Fig.7 Geometric relationship between the optimal opening of the movable guide vane and the fixed guide vane
图7是转轮计算得出的导叶最优开口与固定导叶的几何匹配情况。从图中可以清楚地看出,改造后的转轮A606c与正曲率导叶匹配的最优开口16 mm 时,活动导叶进口角约为25.9°,而映秀湾固定导叶出口角为 24.3°,其最优匹配关系很好。由此可以从固定导叶与活动导叶几何位置关系上判断,原固定导叶和活动导叶匹配情况是合理的。为了进一步分析导叶区域流场分布情况,因此做了固定导叶与活动导叶的 CFD 联合计算分析。以下是转轮额定水头、最优开口下的导叶联合计算CFD分析结果(活动导叶开口为最优开口A0=16 mm)。
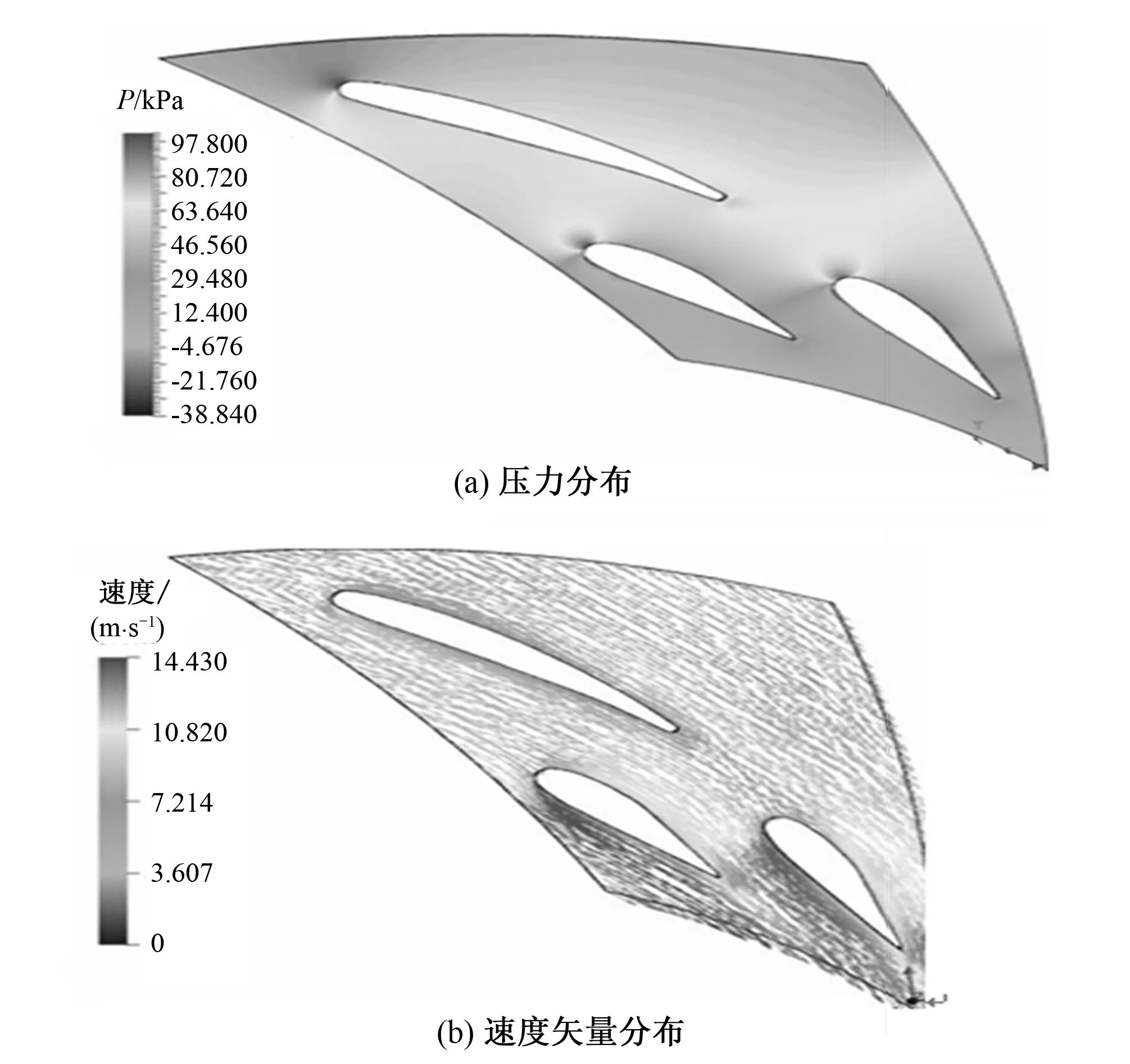
图8 固定导叶和活动导叶压力和速度矢量分布Fig.8 Distribution of pressure and velocity vector of fixed guide vane and active guide vane

图9 固定导叶和活动导叶流线分布(俯视)Fig.9 Distribution of flow lines in fixed guide vanes and active guide vanes(overlooking)

图10 固定导叶和活动导叶区域内部流线分布Fig10 Distribution of flow lines in the area of fixed guide vane and moving guide vane
从导叶CFD分析结果看出,最优开口下,活动导叶进口头部压力驻点基本位 于导叶头部中间附近,速度矢量、流线分布均匀。说明转轮计算最优开口时导叶 区域流态分布良好。 根据 CFD 分析结果,计算了不同开口导叶区的水头损失,并以数值效率的形式表示于图11。由图11 可知,导叶区水头损失最小的开口在17 mm 左右。也就是说固定导叶、 活动导叶联合计算的最优开口与活动导叶、转轮联合计算的最优开口是基本一致的。说明改造后的转轮A606c用于映秀湾电站与其他通流部件的匹配关系是合适的。
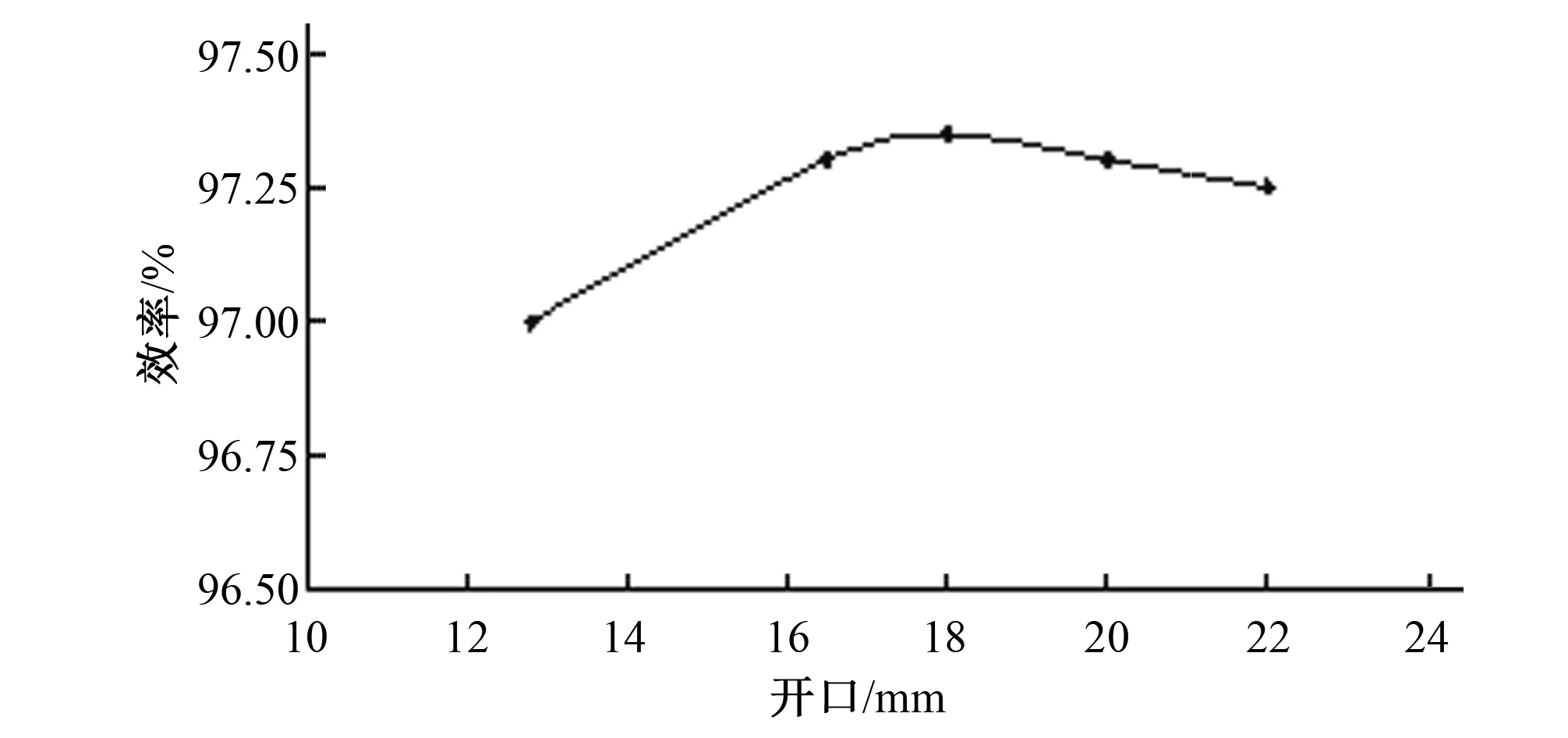
图11 导叶区域数值效率Fig.11 Numerical efficiency of guide vane
3 结果验证
映秀湾电站水轮机机组投入运行之后,对机组运行的相关指标进行监测,如表2所示。待机组停机之后,对机组的过流部件(转轮,固定导叶,活动导叶,蜗壳)进行空蚀检查,如图12 所示。根据表2和图12分析表明,映秀湾电站改造后的机组的相关运行指标都在合理的范围内,过流部件的空化性能良好,说明针对此次改造过程当中的过流部件的分析是合理的,达到了预期的目的。
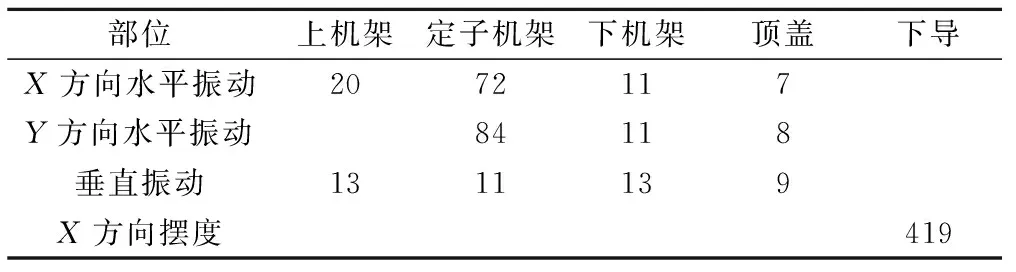
表2 机组运行指标 μm

图12 过流部件空蚀检查Fig.12 Cavitation inspection of overcurrent components
4 结 语
在对映秀湾电站水轮机转轮进行改造之后,利用CFD方法对映秀湾电站水轮机蜗壳,固定导叶,活动导叶进行了计算,得出如下结论。
(1)在对蜗壳和固定导叶进行联合CFD计算表明,蜗壳内的流态以及压力分布情况合理,原蜗壳出流角与固定导叶进口安放角是相匹配的。
(2)在对固定导叶与活动导叶进行联合计算表明,固定导叶与活动导叶的最优开口匹配关系良好。
(3)通过CFD分析发现,在映秀湾电站的改造过程当中,不需要对映秀湾电站水轮机组原过流部件进行修改是合理的,并且在机组的运行监测的数据当中得到了验证。
□
[1] 王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社.
[2] 谢洁飞,李香桂,杨 辉.基于CFD的离心泵内部流场数值模拟与性能预测[J]. 中南林业科技大学学报,2010,30(3):129-132.
[3] 杨敏官,顾海飞,刘 栋,等.离心泵叶轮内部湍流流动的数值计算及试验[J].机械工程学报,2006,42(12):181-185.
[4] 郑 源,鞠小明,程云山.水轮机[M].北京:中国水利水电出版社.
[5] 周晓泉,瞿伦富,吴玉林.水轮机蜗壳和固定导叶内部流动数值模拟[J].清华大学学报(自然科学版),2000,40(8):93-97.
[6] 邓 杰,陈 锐.水力机械UGS NX设计与实例[M].北京:中国水利水电出版社,2009.
