单机十表冗余惯组故障后重构最优估计研究

周维正，李学锋，赵赛君



单机十表冗余惯组故障后重构最优估计研究

周维正1，李学锋1，赵赛君2

（1. 北京航天自动控制研究所，北京，100854；2. 北京无线电测量研究所，北京，100854）

对于单机十表冗余惯组故障后的重构估计，提出一种结合可靠性和精度的重构策略，基于该策略，提出一种在线重构估计方法，对在故障诊断中常用的校验方程残差进行分析；通过时间序列分析的方法确定噪声结构，用卡尔曼滤波对其进行在线估计，估计结果作为重构模型估计精度指标的评价；采用滤波补偿的方法对故障表进行分析计算，该方法绕过了对各轴传感器噪声的估计，直接对投影定理推导的重构模型误差进行分析。仿真结果表明，该算法对传感器精度未知的情况有较强适应性，并有较高精度。

冗余惯组；重构；时间序列分析；Kalman滤波

0 引 言

为提升导航系统可靠性，通常对捷联惯组进行冗余设计。惯组冗余设计方式多样，飞行器领域常见的惯组冗余配置方式有双套捷联惯性测量组合、3套六表捷联冗余方案、单套八表、单套十表、单套十二表捷联惯组方案[1]。本文所说的表个数包括陀螺和加速度计，在分析冗余传感器个数时，不同的冗余配置基于不同的优化指标有不同的安装方式。文献[2]根据导航特性和FDI特性两个性能指标为最优指标，得出正多面体配置方案为最优的结论；文献[3]指出在相同陀螺数的前提下，斜置方案比正交方案可靠性更高。非正交方案虽然有较高的可靠性，但是需要附加计算、精度较正交方案差，另外正交方案有成熟的标定方案和误差模型；文献[4，5]讨论了非正交惯组的标定方法，方案较正交惯组复杂。对于冗余惯组不仅要考虑如何配置，还要考虑如何融合各表信息，输出可靠且精度高的信息，这涉及了故障诊断和重构。故障诊断一直是冗余惯组的研究热点，但重构的研究相对较少。本文首先讨论重构策略，因为重构策略直接影响系统的配置构型、故障诊断的方法和重构的精度，然后对故障后的重构估计给出分析。

本文研究对象是单机十表冗余惯组，由5个陀螺和5个加速度计组成。

1 基础模型

1.1 重构策略

重构策略直接影响系统的配置构型、故障诊断方法和重构的精度。对于五陀螺和五加表的十表构型，本文以陀螺为例，加表的配置与陀螺一致。综合考虑精度和可靠性，五陀螺的配置为三正交轴加两斜置轴的方式。信息输出方式为无故障情况下，选择三正交轴惯性表输出，只在正交表出现故障的情况下，开始重构；重构只针对故障轴。重构流程如图1所示。

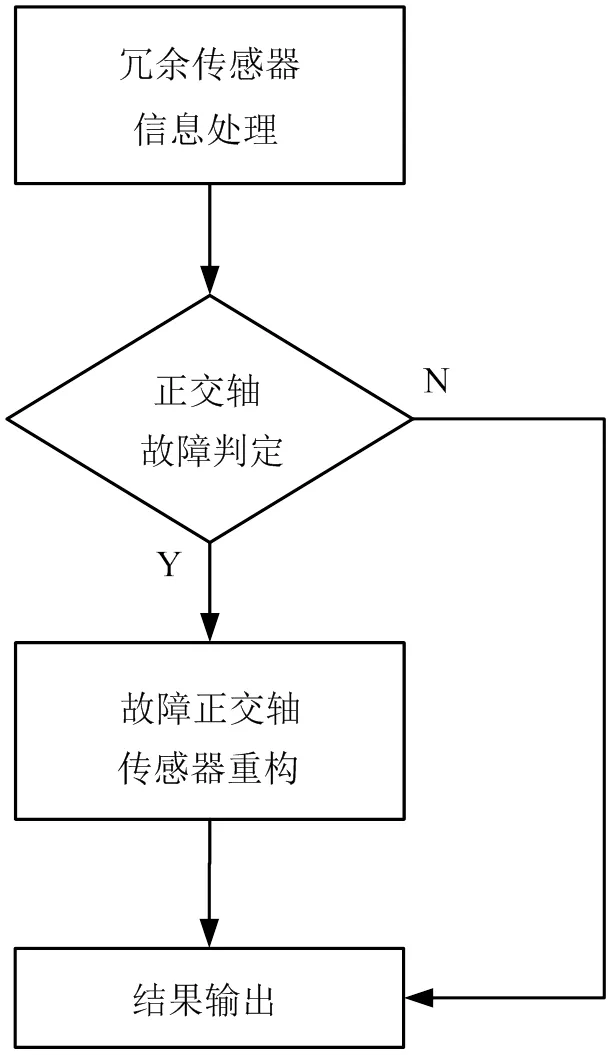
图1 重构策略流程

1.2 冗余配置

三正交两斜置配置结构如图2所示。

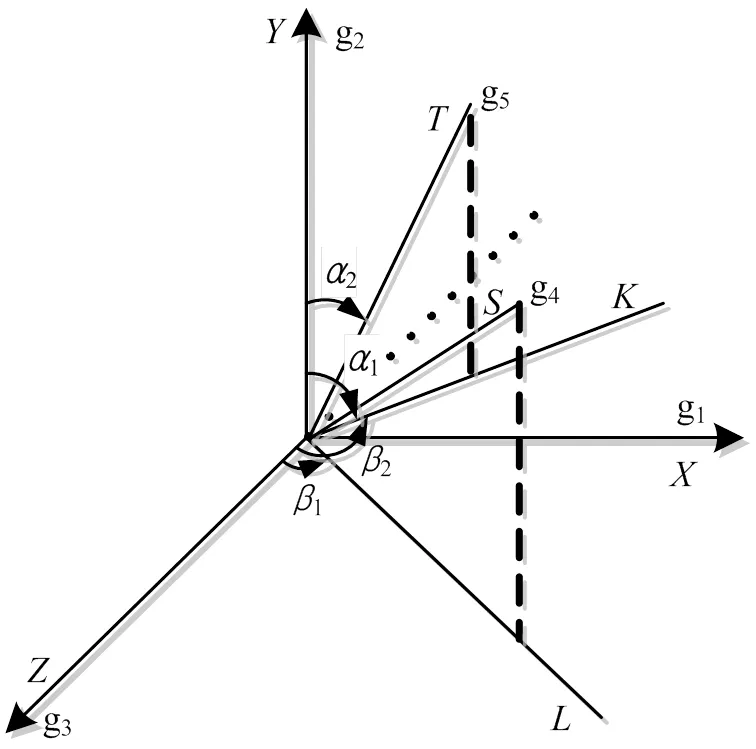
图2 三正交两斜置结构配置示意

g1~g5—陀螺仪，其中g1~g3分别沿，，正交轴正向放置，g4~ g5沿任意方向的两个斜置轴轴和轴布置，惯组坐标指向为向前，向上，与，遵从右手定则；，—g4~g5所在斜置轴，在平面上投影的线；1，2—从轴顺时针旋转至g4，g5所在斜置轴的角度；1，2—从轴逆时针旋转至，的角度

当补偿安装误差参数后，量测方程为

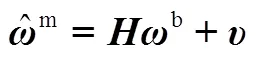
此时的安装矩阵为

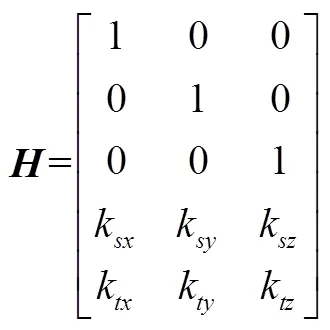
当不考虑异方差的情况下，用式（4）估计三轴导航状态，即：

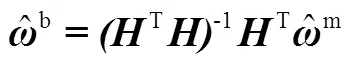
当各陀螺的精度不一致时，不分优劣地使用量测值参与式（4）来估计效果并不是最优，可能还会变差。在量测误差均值为零、方差阵为的情况下，马尔柯夫估计是无偏最优估计[8]：

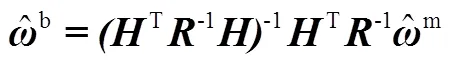
均方误差为

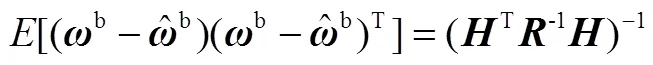
根据冗余配置的基础模型和重构策略，可以看出目前模型的局限性：a）对于噪声的假设过于理想，以在型号中应用较多的光纤陀螺为例，光纤陀螺（FOG）性能主要受常值漂移及随机漂移的影响，其中常值漂移影响FOG的长期性能，可以通过漂移补偿计算消除。随机漂移是一种宽带噪声，可以描述为一阶马尔科夫过程，是影响惯导系统性能的主要因素；b）由于实际应用中，噪声统计特性实时变化，通过离线测定的阵不能实时反应各陀螺的精度信息，需要在线估计值。因此本文针对以上两点研究故障后冗余惯组的最优估计，首先用时间序列分析的方法对校验方程的残差进行分析，残差反映了根据投影原理得到的估计模型的误差，分析该误差对提高重构精度有较大帮助，基于卡尔曼滤波可以对两个重构模型输出给予补偿。

2 校验方程残差时间序列分析建模

对于冗余惯组的故障诊断，通常设计校验方程，通过真值表定位故障表并直接在程序上进行重构，校验公式如式（7）所示。

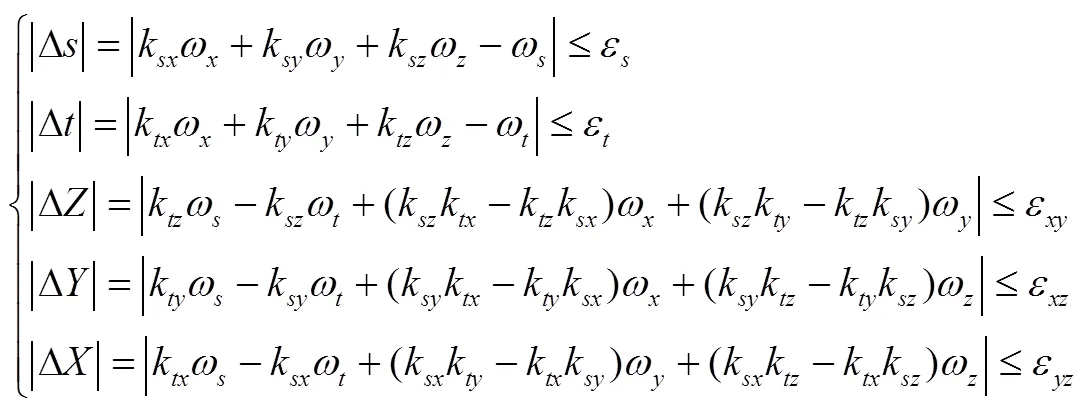
真值表如表1所示。

表1 奇偶校验真值表

Tab.1 Truth Table of Parity Equations Check

失效轴奇偶检测值系统重构的解算程序元 K1K2K3K4K5 无故障00000P0 X00001P1 Y00010P2 Z00100P3 S01000P4 T10000P5 其它故障 —————P6

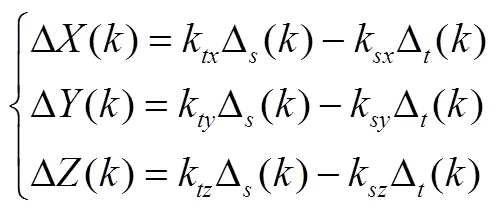
则，估计误差分别为

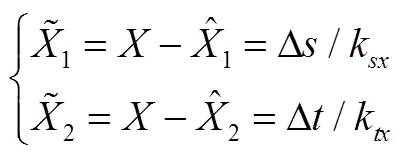
针对残差序列可用来评价所选模型估计的精度，采用时间序列分析的方法对残差序列展开分析。陀螺的随机漂移可用AR(1)、AR(2)表达[9，10]。根据AR模型对校验残差展开建模，确定残差ΔΔ的模型阶数。由于受环境因素以及光纤陀螺稳定性能的影响，光纤陀螺重复启动的随机漂移存在较大的差异，而且单次启动的漂移也会随时间发生变化，导致离线条件下建立的模型不能够很好地应用于实时对准与导航中，确定残差的时间序列结构后，采用在线递推最小二乘法确定模型参数。

3 基于卡尔曼滤波的校验残差评估融合算法

针对残差所建立的时间序列模型建立状态空间模型，以AR(1)模型为例，斜置表的两残差可表示为

转换成卡尔曼滤波的标准形式，则残差状态方程和量测方程分别为

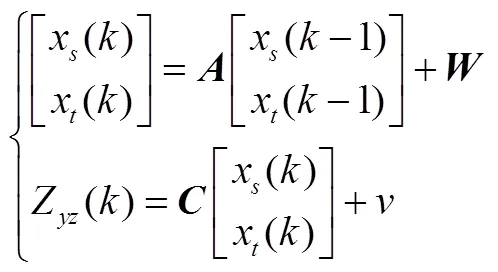
未故障时通过卡尔曼滤波计算稳定后的两模型残差的方差，采用加权平均方法进行融合。

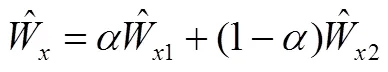
4 仿真算例

给出基于某惯组采样所测的数据进行算法验证，五陀螺为三正交两斜置配置，斜轴正向与三正交轴正向的夹角分别为：125.5°，46.3°和115°；斜轴正向与三正交轴正向的夹角分别为：46.5°，56.5°和118°；误差安装矩阵为

图3给出了5个陀螺每20 ms采样的角增量，其中对前5000步数据进行在线建模，后5000步考察所建模型和算法的有效性。根据分析，所建残差模型为AR(1)模型，根据计算的两校验残差，在线时间序列建模得两组残差模型为

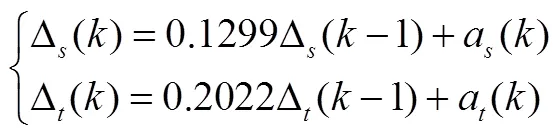
卡尔曼模型为

式中 ；。

表2给出了轴故障后的几种重构模型，图4和图5给出了有补偿模型和无补偿重构模型输出结果的对比图。

表2 重构方案对比

Tab.2 Three Configuration Models in Contrast

方案模型 Y Z S Y Z T Y Z S T补偿式（13）、式（14）

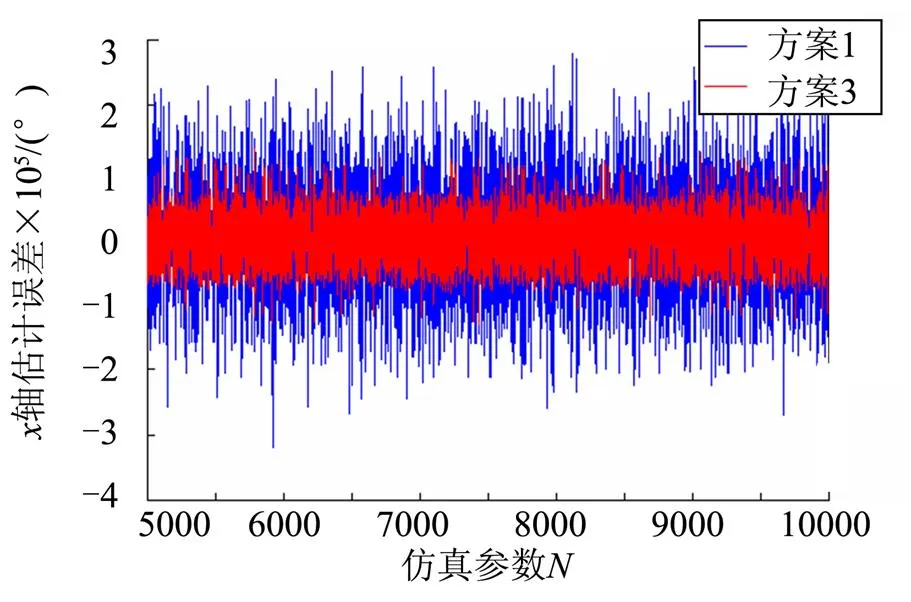
图4 方案1和方案3的估计误差对比

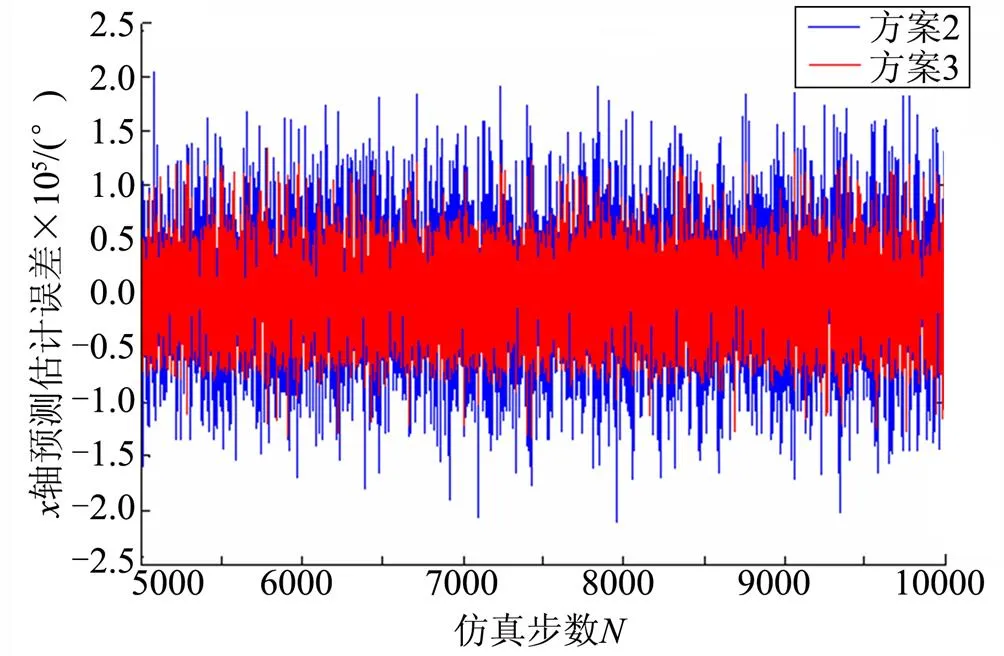
图5 方案2和3的估计误差对比

从图4和图5可以看出，本文算法的误差较两种常见模型有明显提高，经计算误差方差分别降低了77.6%和57.5%。本文方法不需要对各轴传感器的噪声和误差进行假设和在线估计，直接对在冗余惯组故障诊断中常用的校验方程残差进行评估，并以此作为模型估计值的权重分配。仿真结果表明：本文所提方法合理有效。

5 结 论

本文针对三正交两斜置构型提出一种正交为主、斜置为辅的重构策略，基于此策略设计奇偶校验方程，对校验残差采用时间序列分析建模。该方法绕过了对各轴传感器噪声的假设和分析，直接对投影定理推导的重构误差进行分析。采用卡尔曼滤波方法在线对故障后正交轴信息进行补偿，仿真结果表明，估计误差方差有显著减小。

[1] 李学锋, 王青, 王辉, 王通. 运载火箭飞行控制系统设计与验证[M]. 北京: 国防工业出版社, 2014.

Li Xuefeng, Wang Qing, Wang Hui, Wang Tong. Design and verification for flight control system of launch vehicle[M] .Beijing: National Defense Industry Press, 2014.

[2] Shim D S, Yang C K. Optimal configuration of redundant inertial sensors for navigation and FDI performance[J]. Sensors, 2010, 10(7): 6497-6512.

[3] 金宏, 张洪钺. 容错冗余传感器系统与可靠性计算[J]. 航天控制, 1998, 16(2): 38-45.

Jin Hong, Zhang Hongyue. Fault-tolerant redundant sensor system and its reliability calculation[J]. Aerospace Control, 1998, 16(2): 38-45.

[4] 郭鹏飞, 任章. 斜置惯性测量单元的一体化标定技术[J]. 中国惯性技术学报, 2007, 15(3): 377-380.

Guo Pengfei, Ren Zhang. IMU integrated calibrating technique with skewed sensor axes[J]. Journal of Chinese Inertial Technology, 2007, 15(3): 377- 380

[5] 魏莉莉, 黄军, 傅长松, 刘春宁. 带斜置元件的光纤陀螺捷联惯组标定方法[J]. 中国惯性技术学报, 2015, 23(1): 14-19

Wei Lili, Huang Jun, Fu Changsong, Liu Chunning. Calibration method of FOG strapdown IMU with skewed sensor axes[J]. Journal of Chinese Inertial Technology,2015,23(1):14-19

[6] 贾鹏, 张洪钺. 基于奇异值分解的冗余惯导系统故障诊断[J]. 宇航学报, 2006, 27(5): 1076-1080.

Jia Peng, Zhang Hongyue. Fault detection for redundant inertial navigation system based on SVD method[J]. Journal of Astronautics, 2006, 27(5): 1076-1080.

[7] 梁海波. 基于陀螺冗余的微惯性系统关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011: 22-27.

Liang Haibo. Key technique of micro inertial system based on redundant gyroscopes[D]. Harbin: Harbin Engineering University, 2011: 22-27

[8] 秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 西安: 西北工业大学出版社, 2004.

Qin Yongyuan, Zhang Hongyue, Wang Shuhua. Theory of Kalman filter and integrated navigation[M]. Xi’an: Northwestern Polytechnical University Press, 2004.

[9] 王立辉, 孙枫, 季强, 等. LMS 自适应滤波算法在FOG数据处理中的应用[J]. 系统工程与电子技术, 2010, 32(5): 1047-1050.

Wang Lihui, Sun Feng, Ji Qiang, et al. Application of LMS adaptive filtering algorithm in FOG data processing[J]. Journal of Systems Engineering and Electronics, 2010, 32(5): 1047-1050.

[10] 张玲霞. 导航系统故障检测与诊断及其相关理论问题的研究[D]. 西安:西北工业大学, 2004.

Zhang Lingxia. Research on fault detection and diagnosis of SINS and related theory[D]. Xi’an: Northwestern Polytechnical University, 2004.

Research on Estimation for Reconfiguration of Post-fault Redundant Strapdown Inertial Navigation System

Zhou Wei-zheng1，Li Xue-feng1，Zhao Sai-jun2

(1. Beijing Aerospace Automatic Control Institute, Beijing, 100854; 2. Beijing Institute of Radio Measurement, Beijing, 100854）

Considering that estimation of post-fault redundant strapdown inertial navigation system, A strategy combining with accuracy and reliability for reconfiguration is proposed. Based on strategy, a method for estimation is proposed. Parity-check error is analyzed by time series analysis and Kalman filter. The result is used to compensate the reconfiguration output. The method analyzes the error of reconfiguration model instead of every single sensor. The simulation result verifies that the method has a strong adaptability and high precision when there is no measure information of sensors’ noise.

Redundant strapdown IMU; Reconfiguration; Time series analysis; Kalman filter

1004-7182(2018)01-0059-05

10.7654/j.issn.1004-7182.20180112

V448.1

A

2017-01-18；

2017-07-29

国家自然科学基金（61174120）

周维正（1987-），男，博士研究生，工程师，主要研究方向为导航、制导与控制