主动防御的滑模制导算法研究

胡翌玮，蔡远利



主动防御的滑模制导算法研究

胡翌玮，蔡远利

（西安交通大学电子与信息工程学院，西安，710049）

针对主动防御中基于线性化模型设计的制导算法在较大前置角偏差下性能较差的问题，提出防御弹的单向协同滑模制导算法和目标、防御弹的双向协同滑模制导算法。建立了目标、防御弹和拦截弹的相对运动学模型和线性化模型。在目标机动不依赖于防御弹场景下，基于滑模控制理论，选取零控脱靶量（Zero Effort Miss，ZEM）作为滑模面，设计了防御弹的单向协同滑模制导算法。为了进一步提高性能，选取ZEM和零控相对速度（Zero Effort-Velocity，ZEV）作为滑模面，设计了目标、防御弹的双向协同制导算法。通过大量的仿真算例，验证了提出的制导算法的有效性和鲁棒性。

主动防御；零控脱靶量；零控相对速度；滑模控制；鲁棒性

0 引 言

先进导弹防御系统的研究和开发给目标飞行器突防带来了严峻考验。为了躲避拦截弹，提高突防能力，近些年，目标飞行器发射防御弹的主动防御策略引起了国内外学者的广泛研究。文献[1]首次研究了目标、防御弹和拦截弹组成的三体问题；文献[2]在拦截弹信息已知的假设下，利用最优控制理论设计了目标飞行器的最优突防策略和防御弹的拦截策略，但假设拦截弹信息已知并不符合实际；文献[3]假设防御弹未知目标信息，提出了防御弹的自适应制导律，该制导律通过设计一组滤波器估计拦截弹位置、速度、加速度、制导律和制导参数，属于单向协同制导律；文献[4]改进了文献[3]的方法，直接估计零控脱靶量（Zero Effort Miss，ZEM），设计了防御弹的自适应制导算法，减少了计算量；文献[5]基于最优控制理论，提出目标飞行器和防御弹的双向协同自适应制导律。

但上述制导律都是在线性化模型下设计的，在较大的前置角偏差下，实际系统会严重偏离线性化模型，使上述制导律性能变差甚至不可用。为了提高这种情况下的制导律性能，本文基于非线性系统模型，利用滑模控制理论（Sliding Mode Control，SMC），在目标飞行器机动不依赖于防御弹场景下，设计了防御弹的单向协同滑模制导算法。为了进一步提高性能，设计了目标飞行器、防御弹的双向协同滑模制导算法。

首先，建立了目标飞行器、防御弹和拦截弹组成的三体问题的非线性运动学模型和线性化模型，然后，在目标机动不依赖于防御弹时，将ZEM作为滑模面，利用终端投影法近似计算ZEM，进而利用非线性系统模型分析了滑模面的动态特性，并基于SMC理论，设计了防御弹的单向协同制导算法。由于在计算ZEM时，使用到了剩余飞行时间，而剩余飞行时间估计精度直接影响制导算法性能。为了进一步提高性能，引入零控相对速度（Zero Effort Velocity，ZEV）作为另外一个滑模面，来降低制导算法对于剩余飞行时间估计精度的敏感性，设计了目标、防御弹的双向协同滑模制导算法。最后，通过大量的仿真算例，验证了本文建立的制导算法的有效性和鲁棒性。

1 目标飞行器、防御弹和拦截弹组成的三体问题数学模型

目标飞行器、防御弹和拦截弹组成的三体问题如图1所示。拦截弹的任务是拦截目标飞行器，目标飞行器为了实现突防，发射一枚防御弹去打击拦截弹M。假设目标飞行器T和防御弹D之间通信能够保证零延迟（共享当前位置、速度、加速度信息），且已知拦截弹M全部信息（位置、速度、加速度、制导律、制导参数等）。如果未知拦截弹信息，可以利用文献[3]、文献[5，6]中的方法进行估计。假设拦截弹M使用典型制导律（PN，APN，OGL），同时假设T，D，M具有一阶动态特性，时间常数分别为T，D和M，3种飞行器对抗发生在末端，忽略各自的速度变化。

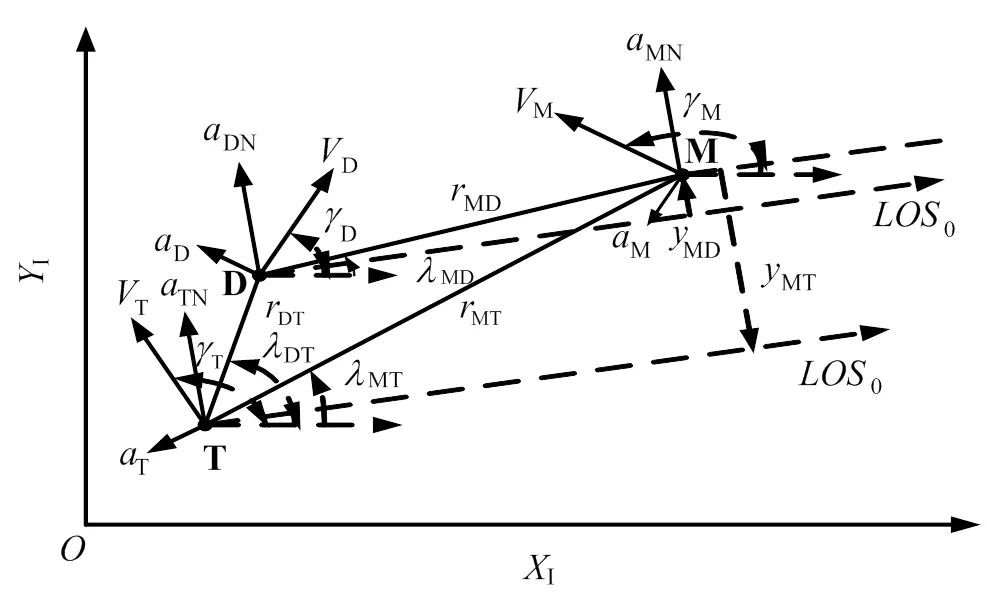
图1 三体对抗数学模型

可以建立相对运动学方程如下：

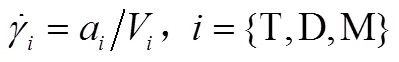
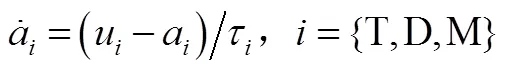
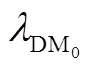
定义3种飞行器加速度和垂直于0方向的加速度分量之间的转换因子为

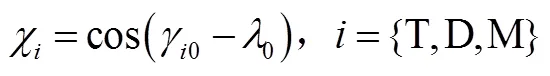
定义M-T对抗问题的状态向量为

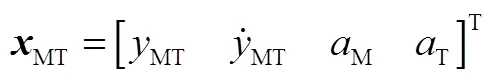
M的典型制导律可表示为

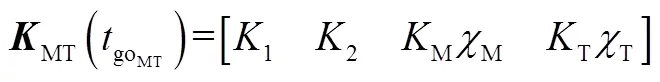
定义T-D-M对抗问题的状态向量为

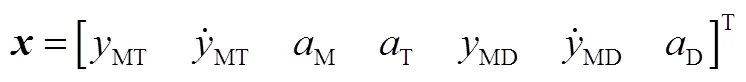
对式（8）进行求导，利用式（4）~（7），可以得到如下线性化的三体对抗模型：

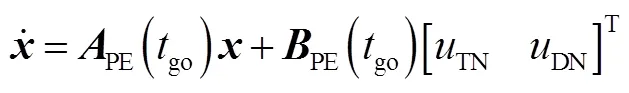
2 防御弹D的单向协同滑模制导算法

在实际中，存在一种情况，目标T不依赖于防御弹D，进行一对一的突防策略，比如Bang-Bang机动、随机机动、最优突防策略等。此时，目标T不需要防御弹D的任何信息，仅有防御弹D利用目标T的信息，构成了单向协同制导问题。

2.1 滑模面设计

为使用滑模控制理论设计防御弹D的制导律，首先需要设计合适的滑模面，本文选取ZEM作为滑模面。这样选择的好处是[7]：a）能够对高阶系统进行降阶处理；b）当系统建模准确时，当系统到达设计的滑模面，防御弹需要的控制输入为零，节省了防御弹的控制能量。但是对于非线性模型式（1）没有ZEM的显示表达式，需要利用线性化模型式（9）近似计算。

利用终端投影法[8]，结合线性化模型式（9），定义零控脱靶量MD为

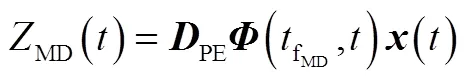
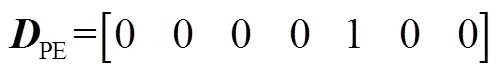
2.2 滑模面动态特性

在得到滑模面的近似表达式后，本节利用非线性运动学模型式（1）分析滑模面的动态特性，利用式（10），得到滑模面1为

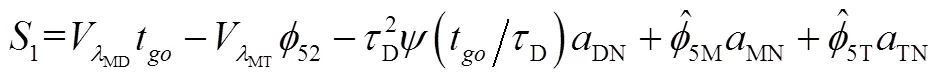
由于线性化模型下，T，D，M在垂直于视线方向的加速度分量计算有一定的误差，进而导致实际的加速度动态特性建模有一定的误差，即：

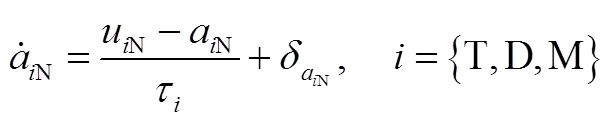
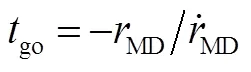
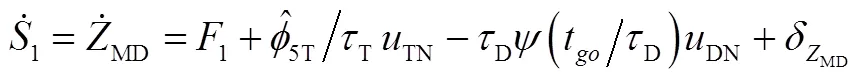
式中

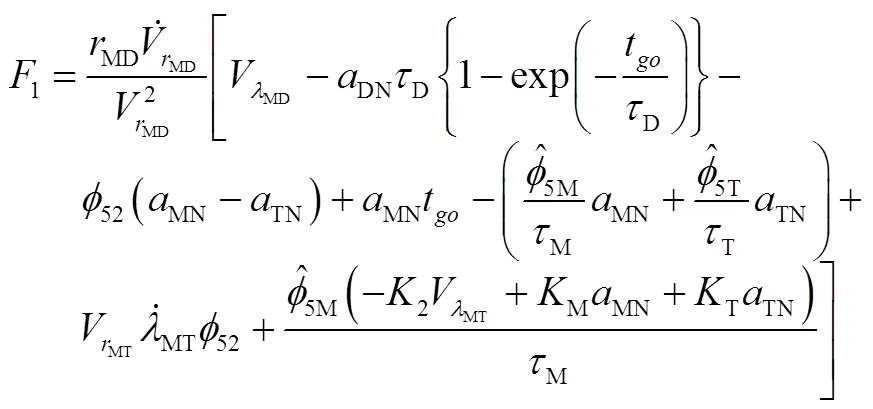
2.3 防御弹D制导算法设计

本节利用SMC设计防御弹的制导律。按照滑模控制的一般原则，防御弹D的制导律由等价控制[9]和变结构控制两部分构成，即DNequvsg。

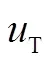
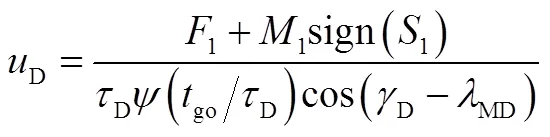
3 防御弹D与目标T双向协同滑模制导算法

当实际攻防对抗环境良好时，目标T可以和防御弹D配合，使得防御弹D能够更加精确打击拦截弹M。此时，需要设计防御弹D和目标T的双向协同制导算法。

3.1 滑模面设计

本节除了选取ZEM作为1个滑模面外，引入另1个ZEV作为第2个滑模面。

由于在计算ZEM时，使用了剩余飞行时间，而在实际中，对于机动目标的剩余飞行时间估计较为困难，造成基于剩余飞行时间设计的制导算法的性能较差。根据文献[10，11]介绍，最终垂直于方向的相对速度直接反映了剩余飞行时间估计误差对制导算法的影响。故而，引入ZEV消除垂直于方向的相对速度，提高制导性能。利用终端投影法，结合线性化模型（9），定义该场景下的ZEV为

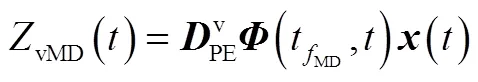
3.2 滑模面动态特性

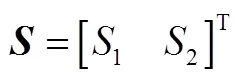
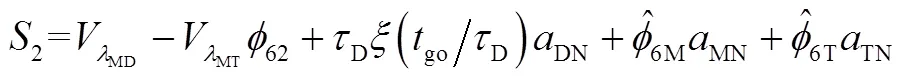
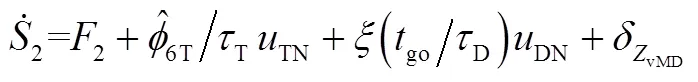
式中

结合式（14），可以得到滑模面的动态特性为

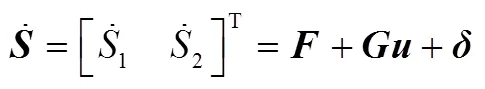
3.3 双向协同制导算法设计

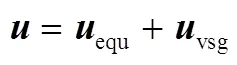
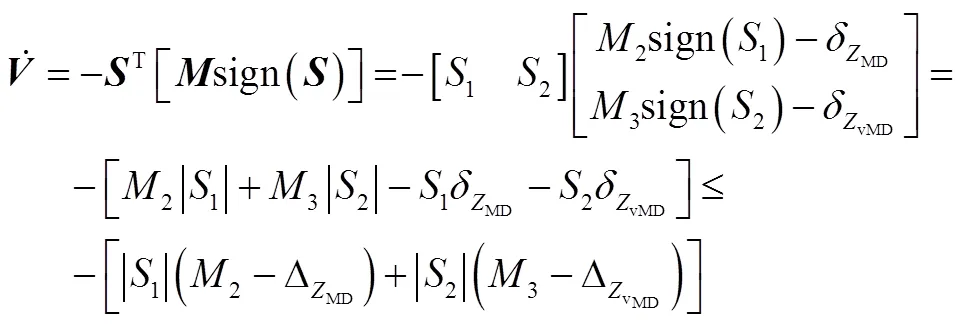
进而有：

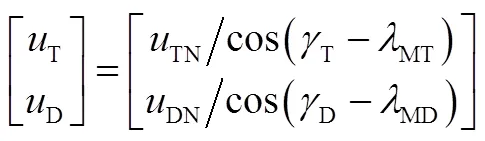
4 仿真与分析

4.1 DOC制导算法仿真与分析

此情况下，目标T的制导不依赖于防御弹D状态，假设目标T做非线性Bang-Bang机动，切换时间sw取5.5 s。进行两组仿真实验：第1组，防御弹D使用本文提出的DOC制导算法；第2组，防御弹D使用传统PN制导，导航系数取3。仿真结果如图2~5所示。

图2是DOC制导算法和PN制导下3种飞行器的轨迹。可以发现，本文提出的DOC制导算法能够精确打击拦截弹，最终的脱靶为0.0089 m，比例导引在于消除视线角转动，由于防御弹D的机动能力的限制，一直处于饱和输入，造成最终的脱靶量为602.405 m。

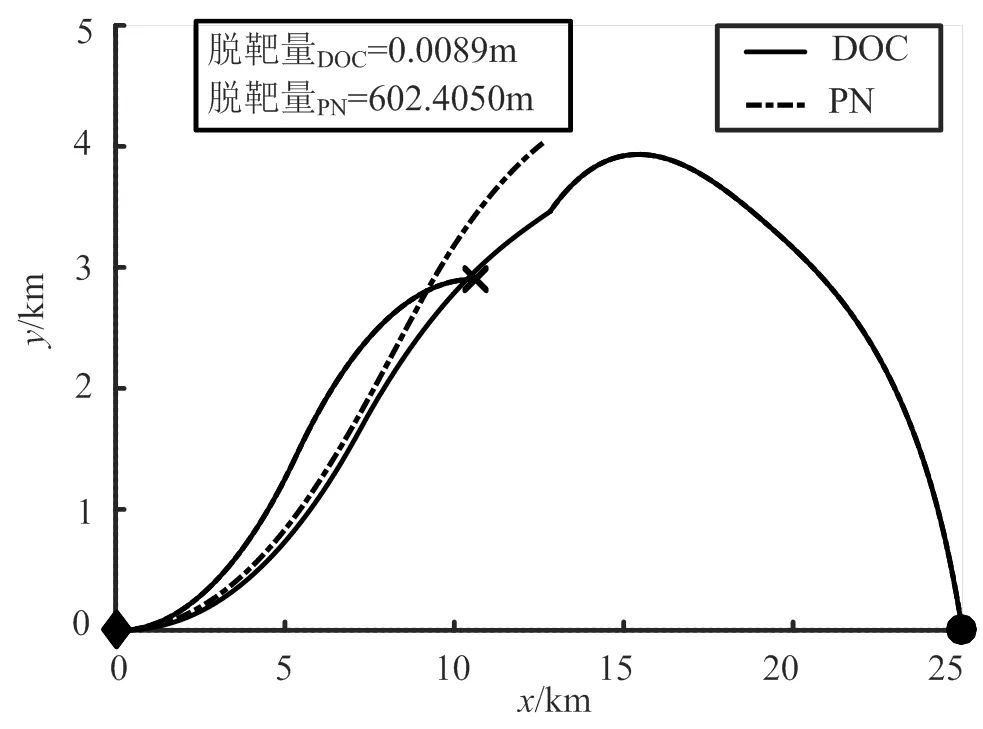
图2 DOC和PN下各飞行器轨迹曲线

◆ —防御弹D的初始位置；●—拦截弹M的初始位置；

× —防御弹D拦截拦截弹M时，目标T的位置

图3为两组仿真中目标T和拦截弹M的加速度曲线。

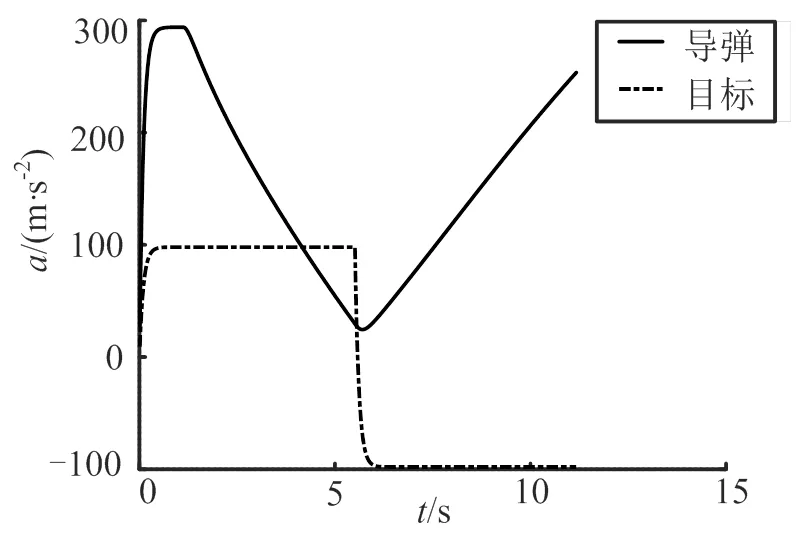
图3 DOC和PN下拦截弹和目标加速度曲线

图4为DOC和PN制导算法下防御弹D的加速度曲线。

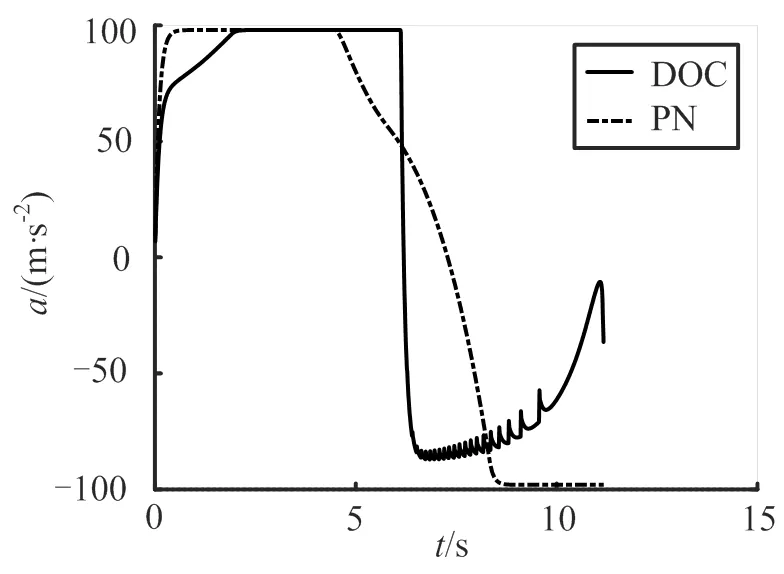
图4 DOC和PN下防御弹加速度曲线

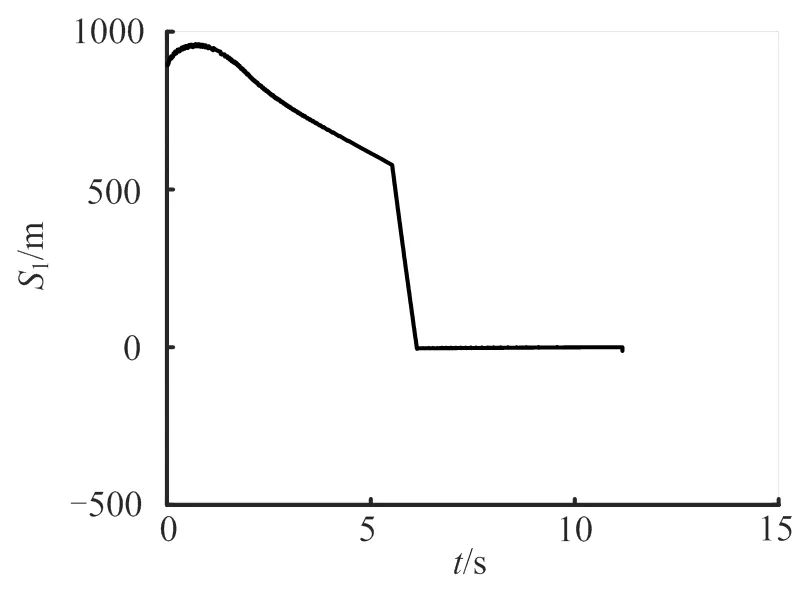
图5 DOC制导算法的滑模面S1曲线

4.2 DTC制导算法仿真与分析

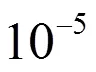
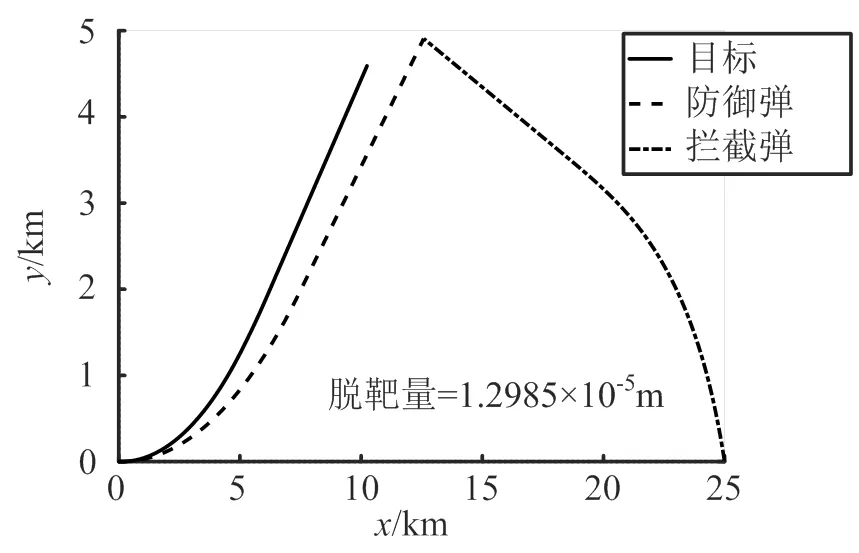
图6 各飞行器轨迹曲线

图7为3种飞行器的加速度曲线。

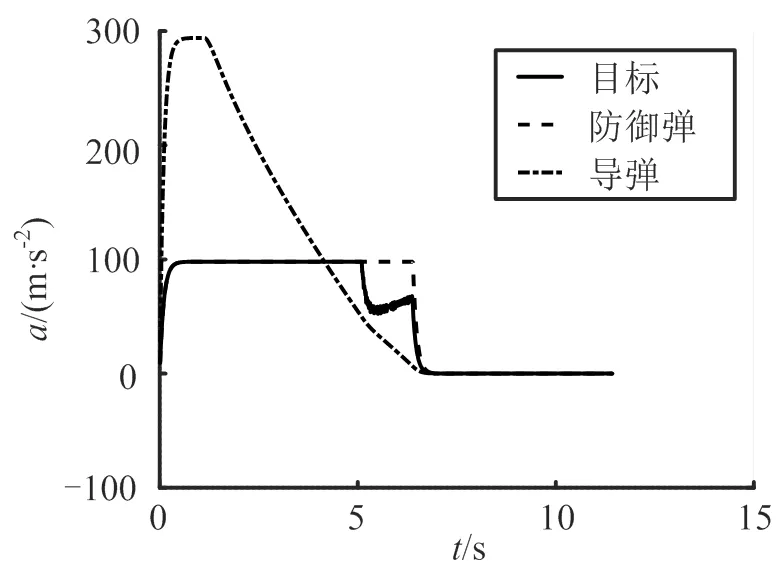
图7 各飞行器加速度曲线

图8 DTC制导算法的滑模面S1曲线

图9 DTC制导算法的滑模面S2曲线

4.3 鲁棒性分析

为了测试本文提出的DOC和DTC制导算法的鲁棒性，令拦截弹M的初始航向角在90.5~269.5°内变化，即前置角偏差在-89.5~89.5°内变化，每隔5°进行一次仿真，得到防御弹D的脱靶量与前置角偏差的曲线如图10所示。

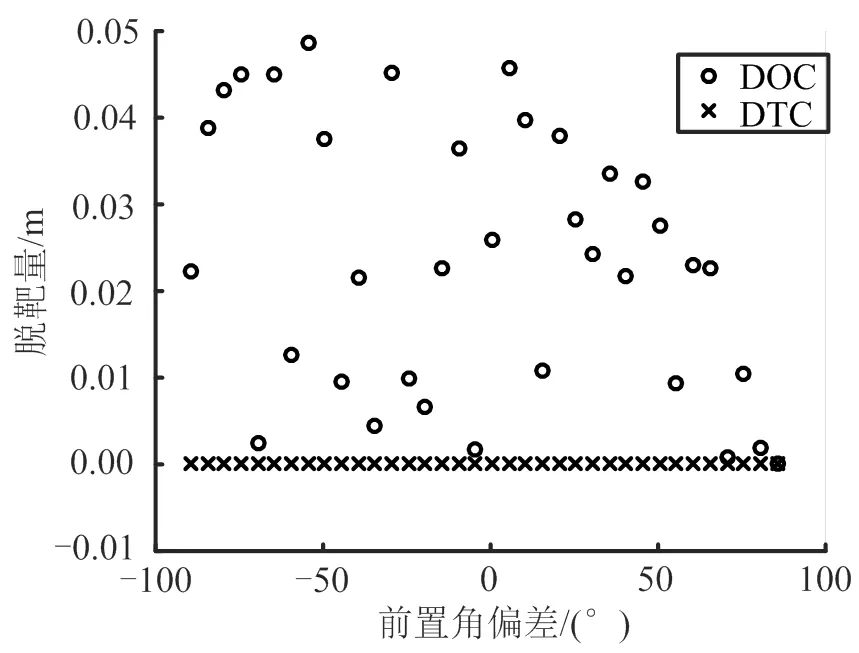
图10 DOC和DTC脱靶量与前置角偏差关系曲线

5 结 论

[1] Boyell R L. Defending a moving target against missile or torpedo Attack[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(4): 522-526.

[2] Tal S. Optimal cooperative pursuit and evasion strategies against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 414-425.

[3] Shaferman V, Shima, et al. Cooperative multiple-model adaptive guidance for an aircraft defending missile[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(6): 1801-1813.

[4] Fonod, Robert, Shima, et al. Multiple model adaptive evasion against a homing missile[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(7): 1578-1592.

[5] 方峰, 蔡远利. 三体对抗中的自适应协同突防策略[J]. 西安交通大学学报: 自然科学版, 2017(4): 72-78+90.

Fang Feng, Cai Yuanli. An adaptive collaborative guidance in three-body engagement[J]. Journal of Xi’an Jiaotong University, 2017, 51(4): 72-78, 90.

[6] 邹昕光, 周荻等. PN制导律多模型自适应辨识滤波方法[J]. 宇航学报, 2016(8): 974-983.

Zou Xinguang, Zhou Di. PN guidance law identification using umlti-model adaptive estimation[J]. Journal of Astronautics, 2016, 37(8): 974-983.

[7] Tal S, Idan, et al. Sliding-mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006,29(2): 250-260.

[8] Applied Optimal Control[M]. USA: Blaisdell, 1969.

[9] Utkin V I. Variable structure systems with sliding modes[J]. IEEE Transactions on Automatic Control, 1997,22(2): 212-222.

[10] BenAsher J Z. Linear quadratic pursuit-evasion games with terminal velocity constraints[J]. Journal of Guidance, Control, and Dynamics, 1996,19(2): 499-501.

[11] BenAsher, Joseph Z Y, et al. Optimal guidance with reduced sensitivity to time-to-Go estimation errors[J]. Journal of Guidance, Control, and Dynamics, 1997,20(1): 158-163.

[12] Kumar, Shashi R, Rao, et al. Sliding-mode guidance and control for all-aspect interceptors with terminal angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2012,35(4): 1230-1246.

[13] Kumar, Shashi R, Rao, et al. Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance, Control, and Dynamics, 2014,37(4): 1114-1130.

Research on Sliding-mode Guidance Algorithm for Active Defense

Hu Yi-wei, Cai Yuan-li

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi′an, 710049)

Aiming at the deteriorated performance of guidance algorithmbased on linearized framework in active defense,this paper presents a sliding-mode control based one way cooperative guidance algorithm for defender, and a sliding-mode control based cooperative guidance algorithm for defender and target. Firstly, the nonlinear kinematics and linearizedmodel of three-body engagement are formulated. Secondly, the zero-effort-miss（ZEM）is selected as the switching surface,and based on sliding-mode control, the defender’s one way cooperative guidance algorithm is designed in the scenario that target’s guidance strategy is independent from defender. Next, in order to improve guidance performance, zero-effort-velocity（ZEV）is selected as another switching surface, the defender and target’s cooperative guidance algorithm are designed. Finally, a lot of simulations are designed to validate the efficacy of the proposed guidance algorithm, and simulation results indicated that the proposed guidance algorithm can maintain robustness under a larger-heading-errors situation.

Active defense; Zero-effort-miss; Zero-effort-velocity; Sliding-mode control; Robustness

1004-7182(2018)01-0063-06

10.7654/j.issn.1004-7182.20180113

TJ765.3

A

2017-05-15；

2017-06-21

国家自然科学基金资助项目(61463029, 61308120)

胡翌玮（1992-），男，硕士研究生，主要研究方向为飞行器制导与控制