基于深度学习的储层物性参数预测方法研究

清华大学自动化系 郑宇哲 叶朝辉

中海油田服务股份有限公司 刘西恩 赵 龙

0 引言

石油测井技术发展至今日，整体趋势上勘探领域不断扩大，研究对象也越来越复杂。以基于地层均质假设的测井响应方程建模方法和统计分析建立回归方程为主的传统测井解释方法，面对较为复杂的研究对象时，识别精度往往不够准确，并且多数情况下，对技术人员的经验要求较高[1]。而当前发展迅速的人工智能技术可以从已有的历史数据中自主发现和学习规律，并依此对新的样本数据进行识别或预测。它可以针对测井数据的特点进行全方面的信息挖掘，其处理数据的思路和方法与传统理论完全不同，与之相比有着独到的优点[2]。前人在使用机器学习方法进行测井解释方面已经做出了一些研究，但基本都是使用一些浅层结构的模型，在样本的选取和训练过程中的细节方面的考虑也稍显欠缺，因此最终得到的预测精度还有提升空间[3-6]。本次研究紧密结合实际生产，采用了深度BP神经网络、聚类、RBM等多项深度学习技术，并且在数据的预处理阶段和训练过程中采用了多种方法来提高其准确率，最终在孔隙度储层参数上获得了较高的识别精度，说明基于深度学习的新型测井解释方法在实际生产中具有一定的应用价值。

1 研究背景

研究区域位于山西省内的某作业区，为中海油田服务股份有限公司的开发区域。经过甄选，以一段连续的共计300多米的测井段作为研究对象，其采样间隔为0.1米，共计3000多个测井数据点。在该测井段内使用了多种测井项目，共包括井径、井斜、中子、声波、伽马、光电、密度、自然电位、阵列感应电阻率、深浅测电阻率、泥质含量等。最终探明该井段包含多种类型的储层，包括干层、差气层、气层。该测井段样本充足且样本多样性丰富，为使用深度学习进行研究提供了良好的先决条件。

2 深度学习方法预测储层物性参数

2.1 特征选取

深度学习模型最终预测性能的好坏很大程度上与输入特征的选取有关。

由于本井段测井项目较多，因此可供选择的输入特征较多。对于一个储层物性参数，本文采用如下的方法确定输入特征：

(1)采用SIS（Sure Independence Screening）算法[7]：生成若干组服从标准正态分布的随机变量，计算这些随机变量与响应变量之间的相关系数，取其中最大值作为临界值T。之后，再计算每一个特征与响应变量之间的相关系数，初步筛选出相关系数大于T的特征。

(2)结合测井技术人员的经验与SIS方法的计算结果，在初步筛选的基础上进一步选取可靠的输入特征。

以孔隙度为例，表1所示为经过筛选后得到的输入特征。

表1 孔隙度的输入特征

2.2 使用BP神经网络作为预测模型

大量的勘探实践和理论研究已经证明了地层的非均质性以及测井数据和储层物性参数之间的响应的非线性性质，而Hornik等人证明[8]，三层以上神经网络具有可逼近任意连续函数的特点。BP神经网络常用于解决一般的非线性响应问题，因此考虑使用其来建立测井数据到储层物性参数之间的映射关系[9]。

神经网络结构的确定没有一般性的通用法则，结构过于简单容易造成欠拟合，结构过于复杂则容易造成过拟合[11]。由于网络参数较多时也会要求训练样本数目增大，为与实际生产相结合，研究需要同时满足结构尽量简单和足够的预测精度两个条件。以孔隙度为例，采用“试凑法”，对于多种结构进行重复实验得出，隐层的层数选取为2层比较合理，最终确定网络结构为8X6X3X1，如图1所示。

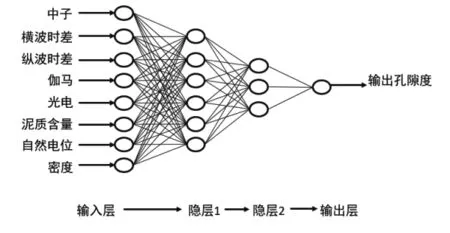
图1 预测孔隙度的神经网络结构示意图

2.3 样本选取

在实际生产中，对于新开发的区域，测井数据往往有限。为与将来的实际生产对接，希望在所用到的训练数据尽量少的情况下，还能保证较高的预测精度。因此对于所给的数据集，应将小部分取出用于训练，而将大部分留下作为测试集，故训练样本集应具有一定的代表性，充分覆盖多种类别的储层，且各个类别之间的样本数目应大致相同。

具体方法为：（1）将3000多个测井数据点进行自底向上的层次聚类处理。由于该井段的储层类别划分为干层、差气层、气层三类，因此选择目标聚类簇数为3。（2）聚类完成后，在3个簇中再按照一定的比例抽取数据点，组合成训练集[13]。由此得到的训练集具有较好的代表性。

改变抽取的比例，组成样本容量不同的训练集合，采用简易的BP算法对2.2中所确定结构的神经网络进行训练，使用150个数据点构成的验证集观察随着训练集样本容量的增加时网络性能的变化情况，实验结果如图2所示。

图2 验证集准确率随训练样本容量变化情况

由图2可见，样本容量在300以上时，模型的精度不再随容量的增加有明显提高，波动的范围可以认为是训练过程中的随机因素导致。即在实际生产中，若收集到300个以上比较具有代表性的样本点时，使用本文提出的方法预期可以得到较高的预测精度。经过调整最终将孔隙度模型的训练集样本容量确定为315个。

2.4 训练过程与结果

本次研究采用了先使用受限玻尔兹曼机（Restricted Boltzmann Machine，以下简称为RBM）进行无监督预训练，再采用有监督方法调优的训练模型策略[14]。

RBM其结构如图3所示，是由一个可见层和一个隐层组成的层内无连接、层间无向全连接的一种概率神经网络。

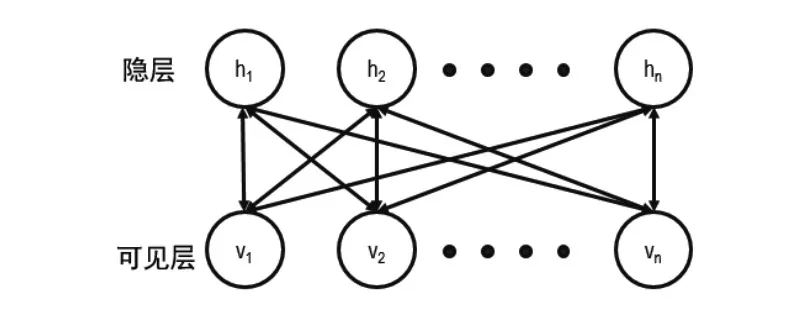
图3 RBM结构示意图

因此，可将神经网络相邻的两层看作一个RBM，上一层的响应即为下一层的输入。而实际应用表明，使用RBM训练得到的权值来初始化BP神经网络，有助于解决传统BP神经网络随机初始化带来的容易陷入局部极小值点和收敛过慢的问题，从而提升网络预测精度。本次研究采用了CRBM（Continuous Restricted Boltzmann Machine）模型[15]，使用CD（Contrastive Divergence）算法[16]，对BP神经网络进行逐层预训练。设置迭代到重构误差以均方根误差衡量时达到0.01时预训练完成。

在有监督训练调优阶段，传统的梯度下降法遍历整个训练集后才对权值做一次更新，计算量大导致训练缓慢，本次研究采用小批次梯度下降法，即每次从训练集中抽取一批样本计算梯度，完成权值的更新。为了加快收敛，引入了动量和衰减学习率的机制，其迭代公式为：

其中ΔWn为本次权值更新量，ΔWn-1为上次权值更新量，Δ J为梯度，γ、η分别为动量参数和学习率。

设置迭代轮数上限为50000，目标收敛精度为0.0001，动量参数γ取0.9，学习率η初始取0.01，每迭代100轮将其乘以0.5。以2.3中确定的样本容量，在聚类之后的总计3000多个样本中，抽取315个样本作为训练集，另外抽取100个样本作为验证集，将其余的样本均作为测试集，某一次训练的误差变化趋势如图4所示。

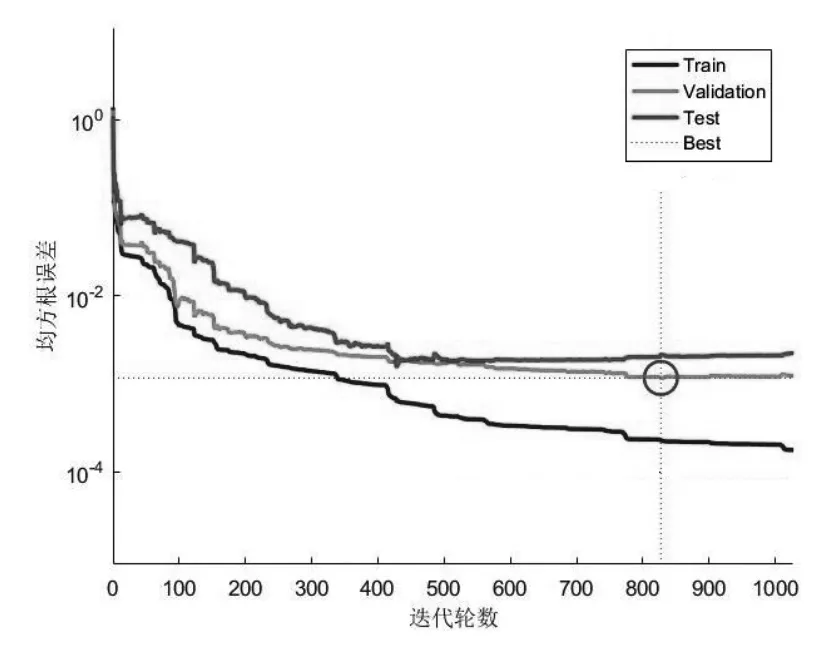
图4 训练过程误差变化趋势

训练过程引入了“早停止”机制来防止过拟合，即检测到经过一定迭代轮数，验证集的误差不再下降时，便停止训练。图中验证集曲线上的标记点为误差最低点。最终经过1020轮迭代后训练结束。此时得到训练集上网络预测的孔隙度和测井数据的孔隙度的相关系数达到0.9938。

之后采用该模型对全井段进行预测，得到相关系数为0.9788，绘制散点图如图5所示（将孔隙度归一化到[-1,1]之间进行作图，下同）。选取部分井段绘制曲线图6所示（隐去了横轴的具体深度）。由图6可见，网络预测结果和测井数据高度重合，说明预测结果精度较高。

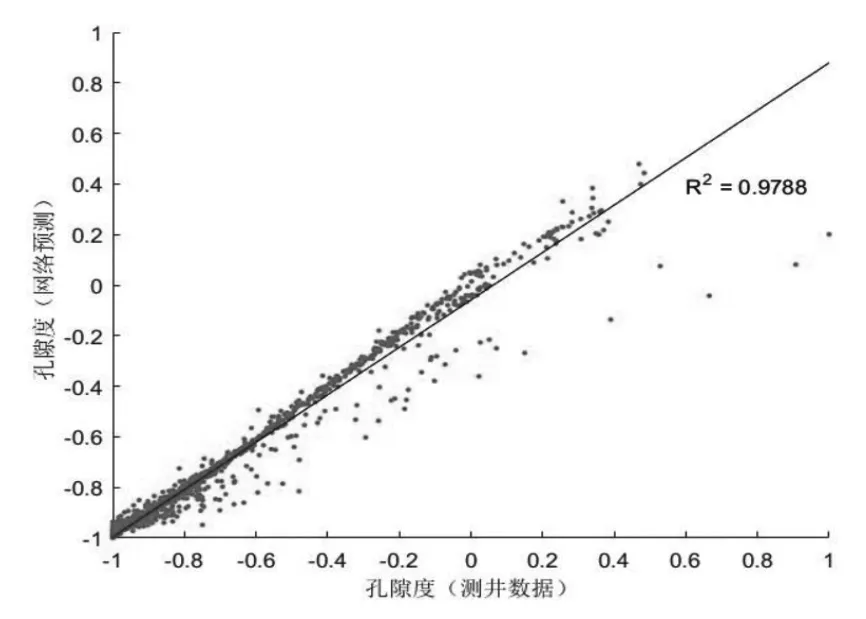
图5 全井段孔隙度预测结果

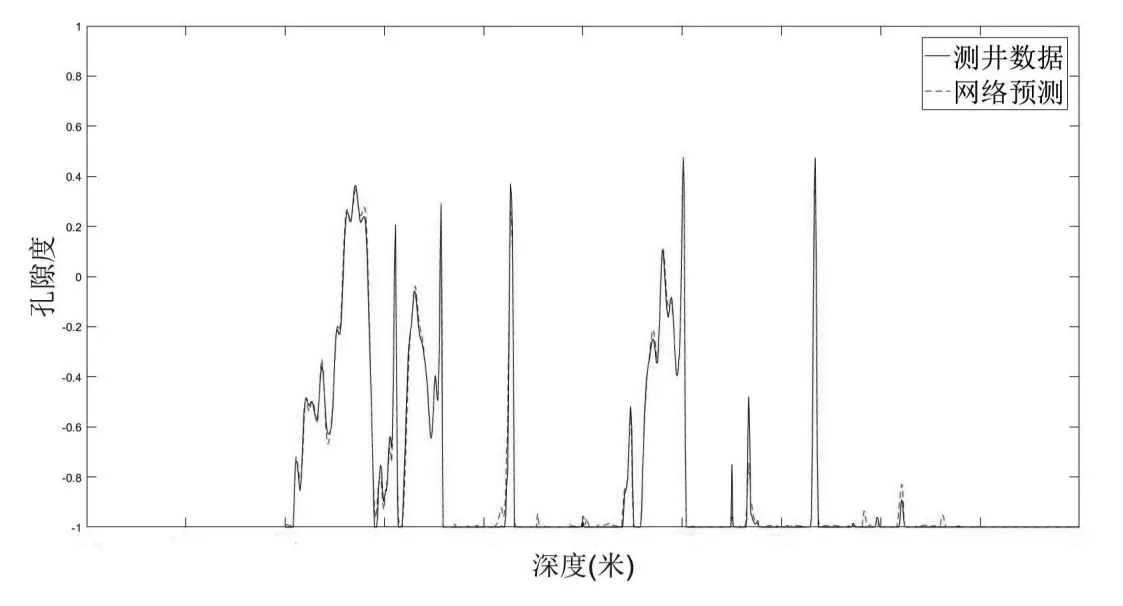
图6 全井段测井数据与网络预测孔隙度曲线

3 结论

山西省某作业区内的该测井段，其样本类型丰富，适合使用深度学习方法对其进行研究，搭建储层物性参数预测模型。具体步骤如下：

（1）采用SIS算法并结合经验选取预测变量。

（2）采用BP神经网络作为预测模型，确定模型结构，并且为切合实际生产情况，确定了训练集的样本容量。

（3）使用聚类方法预处理数据，从聚类结果中抽取一定的比例组成训练集、验证集。

（4）采用无监督预训练+有监督调优的训练策略：无监督阶段将神经网络每两层看作一个CRBM，采用CD算法预训练神经网络；有监督阶段使用引入动量和衰减学习率机制的小批次梯度下降法加快收敛，并引入了“早停止”措施防止过拟合。

使用该流程对孔隙度进行了预测，得到了良好的预测结果，说明本文提出的方法在实际生产中有一定的应用价值。

[1]杨斌,匡立春,孙中春,等.神经网络及其在石油测井中的应用[M]北京：石油工业出版社,2005：94-98.

[2]宋文广,李振智,陈汉林,等.地层原油物性参数大数据处理方法研究[J].新疆大学学报(自然科学版),2016,33(3)：270-274.

[3]张伟,师奕兵,周龙甫,等.基于改进的粒子群-小波神经网络的固井质量智能评价[J].信息与控制,2010,39(3)：276-283.

[4]边会媛,潘保芝,王飞,等.基于横波测井资料的神经网络火山岩流体性质识别[J].测井技术,2013,37(3)：264-268.

[5]李民,陈科贵,杨智,张家浩,刘鑫.基于模式识别的稠油油藏复杂岩性识别方法[J].测井技术,2017,41(4)：453-457.

[6]ALI Dashti,EBRAHIM Sefidari.伊朗扎格罗斯地区Mansuri油田储集层物性模拟[J].石油勘探与开发,2016,43(4)：559-563.

[7]Fan J Q,Lv J.Sure independence screening for ultrahigh dimensional feature space[J].Journal of the Royal Statistical Society：Series B(Statistical Methodology),2008,70(5)：849-911.

[8]K Hornik,M Stinchcombe,H White.Multilayer feedforward networks are universal approximators[J].Neural Networks,1989,2(5)：359-366.

[9]赵军龙,李纲,麻平社,等.神经网络在石油测井解释中的应用综述[J].地球物理学进展,2010,25(5)：1744-1751.

[10]王娜娜,张国英,王明君,等.改进的BP神经网络在石油测井解释中的应用[J].北京石油化工学院学报,2008,16(1)：17-20.

[11]侯祥林,胡英,李永强,等.多层人工神经网络合理结构的确定方法[J].东北大学学报(自然科学版),2003,24(1)：35-38.

[12]范佳妮,王振雷,钱锋.BP人工神经网络隐层结构设计的研究进展[J].控制工程,2005,(S1)：109-113.

[13]韩习武,赵铁军.一种聚类质量的评价方法及其应用[J].哈尔滨工业大学学报,2009,41(11)：225-227.

[14]Hinton.G.E et al.A fast learning algorithm for deep belief nets[J].Neural Computation,vol.18,2006,1527-1554.

[15]H Chen,A Murray.A Continuous Restricted Boltzmann Machine with a Hardware-Amenable Learning Algorithm[J].Lecture Notes in Computer Science,2002,2415：358-363.

[16]Hinton G E.Training products of experts by minimizing contrastive divergence[J].Neural Computation,2002,14(8)：1771-1800.