一类分数阶超混沌系统的自适应有限时间控制

邵克勇,韩 峰,郭浩轩

0 引 言

分数阶微积分已有超过三百多年的历史。近几十年,分数阶微分方程已被证实比传统的整数阶方程更加可行[1-4],因此,分数阶微积分已成为工程、数学和物理等科学领域中非常重要的一部分。在许多实际系统中,分数阶混沌可能会导致系统的振荡或不规则运动。因此,为消除混沌行为,混沌控制已成为非线性控制领域的重要问题。目前许多控制方法已成功运用到分数阶系统中,如主动控制[5]、T-S模糊控制[6]和滑模控制等[7,8]。滑模控制是一种简单有效的控制方法,因其具有较强的鲁棒性和抗干扰能力而被广泛关注[9]。

许多研究学者采用混沌控制消除混沌,通常他们多是考虑系统的渐近稳定,然而有限时间稳定可能在某些实际情况下更有意义。20世纪50年代,Kamenkov[10]首次提出了有限时间稳定的概念。有限时间稳定系统不仅有更快的收敛速度,而且有更好的鲁棒性和抗干扰性能[11]。Amato[12]和Garcia[13]研究了连续时间系统和离散时间系统的有限时间稳定问题。文献[14,15]将有限时间的一些结果拓展到线性、连续系统中。Wang等[16]解决了超混沌系统的有限时间控制问题。然而,这些研究主要是针对于整数阶系统,而对分数阶系统有限时间控制研究的结果还很少。笔者针对不确定参数的分数阶超混沌系统的有限时间稳定问题,通过构造全新的李雅普诺夫函数并设计自适应有限时间控制器,实现了系统的自适应有限时间稳定。该方法简单有效,可使系统的状态变量在有限时间内收敛到平衡点,具有良好的鲁棒性能,并通过数值仿真验证了该方法的准确性及有效性。

1 分数阶微积分基本理论

定义1 连续函数f(t)的α阶Caputo分数阶导数定义为[17]

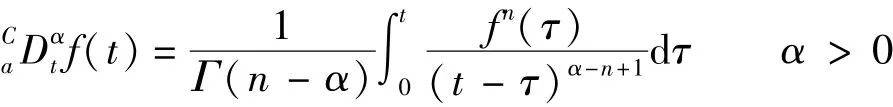
其中n是整数,α为分数阶系统的阶次,满足n-1＜α≤n,Γ(·)是Gamma函数。

定义2 Gamma函数定义[18]

考虑如下非线性分数阶混沌系统

其中α∈(0,1),初始条件x(t0)=x0,t0≥0,f:[t0,∞]×Ω→Rn在t上是分段连续的,并且在[t0,∞]×Ω上满足局部Lipschitz条件,Rn是n维欧氏空间。同时,Ω⊂Rn是一个包含原点x=0的区域。假设对初始值x(t0)=x0的系统(1)总存在唯一解x(t)∈C1(t0,∞),C1(t0,∞)是在区间(t0,∞)上的连续可导的空间。

引理1 若0CDαtx(t)≤0,那么x(t)在[0,+∞)上单调减少;同理,若0CDαtx(t)≥0,则 x(t)在[0,+∞)上单调增加[19]。

引理2 ～x=0是系统(1)的平衡点,并且D是一个包含原点的区域,且D⊂Rn。若存在Lyapunov函数V(t,x(t)),且V(t,x(t)):[0,∞]×D→R是连续可导函数,并且关于x满足局部Lipschitz条件,R是实数集,使

其中t≥0,x∈D,α∈(0,1),αi(i=1,2,3),a和b都是任意正的常数,则系统(1)是Mittag-Leffler稳定的。若在Rn上亦满足式(2)和式(3),则系统(1)是全局Mittag-Leffler稳定的[20]。

引理3 Mittag-Leffler稳定和全局Mittag-Leffler稳定表明系统渐近稳定[20]。

定义3 若对任意的初始值x0,存在ε＞0,使对所有t＞t0,有‖x(t)‖≤ε,则阶次为α(0＜α＜1)的系统(1)的0解是稳定的。此外,当t→∞,有‖x(t)‖→0,则系统(1)的0解是渐近稳定的[21]。

引理4 若x(t)∈Rn是连续可导函数。则对任意时间常数t≥0,有[21]

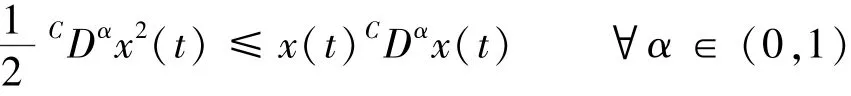
引理5 Jensen不等式

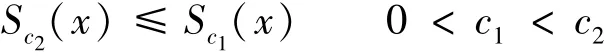
1) α1‖x‖a≤ V(t,x(t))≤ α2‖ x‖ab; 2) kV1/β(t,x(t))≤ α3‖ x‖ab; 3)≤-α3‖x‖ab。

其中α∈(0,1),αi(i=1,2,3),a,b,k和β都是任意的正常数,且β＞1,则系统(1)是有限时间稳定的,且系统(1)的稳定时间满足[20]

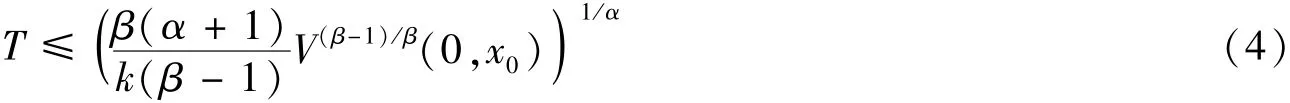
由引理6中的条件1)和3)可知,系统(1)是Mittag-Leffer稳定的。通过引理3可知,系统(1)是渐近稳定的。结合条件2)可得:V(t,x(t))≤-kV1/β(t,x(t))。 因此,只要系统(1)是Mittag-Leffer稳定并满足V(t,x(t))≤-kV1/β(t,x(t)),则系统(1)即为有限时间稳定的。

2 自适应有限时间控制

考虑分数阶超混沌Lorenz系统

其中x=[x1,x2,x3,x4]T是系统的状态变量,u=[u1,u2,u3,u4]T是待设计控制器,f(x)是非线性部分,A是带有未知参数a,b,c和d的系数矩阵。由式(5)可见,x=0是系统(5)的平衡点。

当不考虑控制器u时,系统具有分数阶超混沌Lorenz系统结构。通过对分数阶超混沌系统的离散化及Matlab编程计算,对4个参数、分数阶阶次α及初值变化取值并进行大量计算得到,当参数a=10,b=8/3,c=28,d=-1,0.9≤α＜1时,系统处于超混沌状态。选取如上参数并取α=0.9,任选初值x1(0)=x2(0)=x3(0)=x4(0)=0.1时,分数阶超混沌Lorenz系统的相图如图1所示。

图1 阶次为0.9时分数阶超混沌Lorenz系统的相图Fig.1 Phase diagram of fractional order hyperchaotic Lorenz system with order 0.9

定理1 系统(5)在控制器

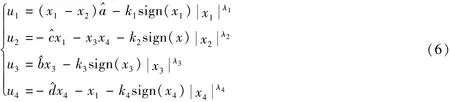
作用下是自适应有限时间稳定的。其中ki＞0(i=1,2,3,4),^a,^b,^c,^d分别为a,b,c,d的估计值。参数自

适应率设计如下

证明 选取Lyapunov函数

由引理4可知

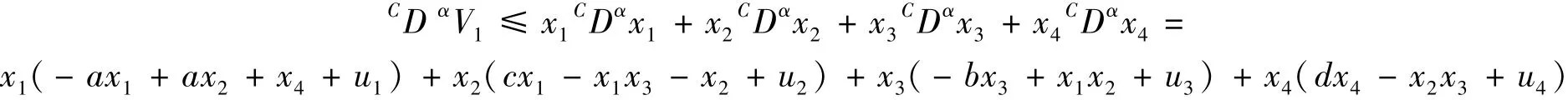
由于 ki＞0(i=1,2,3,4), 故可得CDαV(X,t)＜0。

因CDαV(X,t)＜0,即负定,所以一定存在 α3＞0, 使CDαV(X,t)≤-α3‖X‖2。 故由引理2 可知, 系统(5)是Mittage-Leffler稳定。由CDαV(X,t)的负定性可知,0,因此,该控制器保证系统的解是全局有界的。由于CDαV(X,t)＜0,由引理1,V(X,t)关于时间t是单调递减的,因此V(X,t)≤V(X,0),且V(X,t)≥0,0是下界。同时也可得(t)≤2V(X,0)。当x21+x22+x23+x24≤1时,有

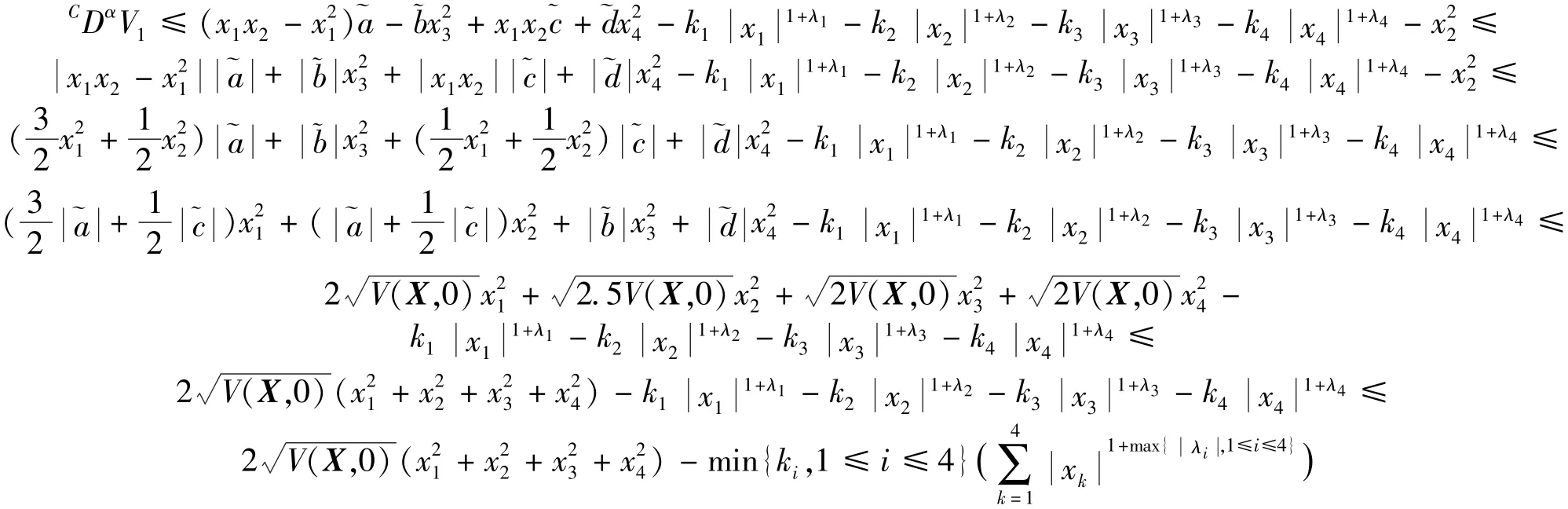
定义¯k=min{ki,1≤i≤4},¯λ=max{λi,1≤i≤4}。由引理5,当,有

令β=2/(1+¯λ),则CDαV1≤-δ¯k(2V1)1/β。

3 数值仿真

为证实带有未知参数的分数阶超混沌Lorenz系统的自适应有限时间控制器(6)及自适应控制率(7)的准确性,对其进行数值仿真,仿真结果如图2和图3所示。系统的仿真时间为10 s,分数阶超混沌Lorenz系统(5)的参数值选取如下:a=10,b=8/3,c=28,d=-1,α=0.9;任选初始条件为:x(0)=(3,2,-2,4),^a(0)=^b(0)=^c(0)=^d(0)=0。根据定理1,为方便计算,选取参数 k1=k2=k3=k4=6(参数可以不同),λ1=λ2=λ3=λ4=0.5,即 β=4/3。稳定时间=3.4 s。

图2 分数阶超混沌Lorenz系统的状态变量随时间变化图Fig.2 The state variables of the fractional-order hyperchaotic Lorenz systems

由图2和图3可见,系统在3 s内便可消除混沌,并使系统的状态变量在有限时间内稳定到平衡点O(0,0,0,0),收敛速度很快,同时实现了未知参数的辨识。

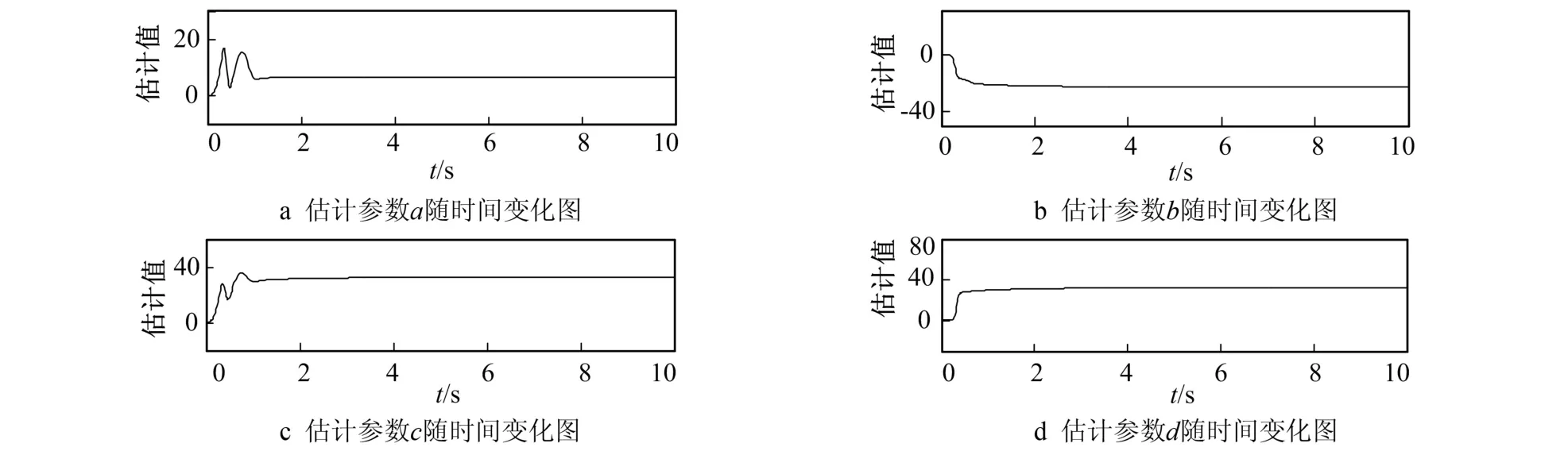
图3 估计参数随时间变化图Fig.3 The time variations of the estimated parameters

为分析该控制方法的鲁棒性,给出扰动模型

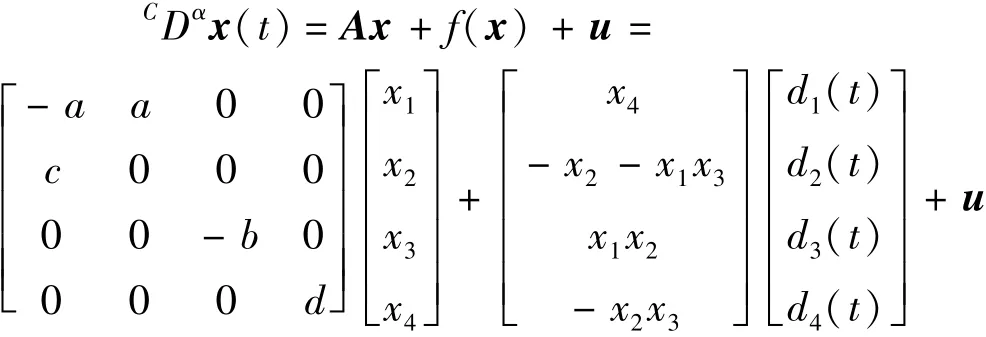
其中di(t)=0.5 sin(10xi),i=1,2,3,4。任选初始条件:x(0)=(2,0,6,-4),α=0.95,^a(0)=^b(0)=^c(0)=^d(0)=0。为方便计算,选取参数k1=k2=k3=k4=8,λ1=λ2=λ3= λ4=0.6, 即 β =1.25。 稳 定 时 间=2.87 s。仿真结果如图4和图5所示。

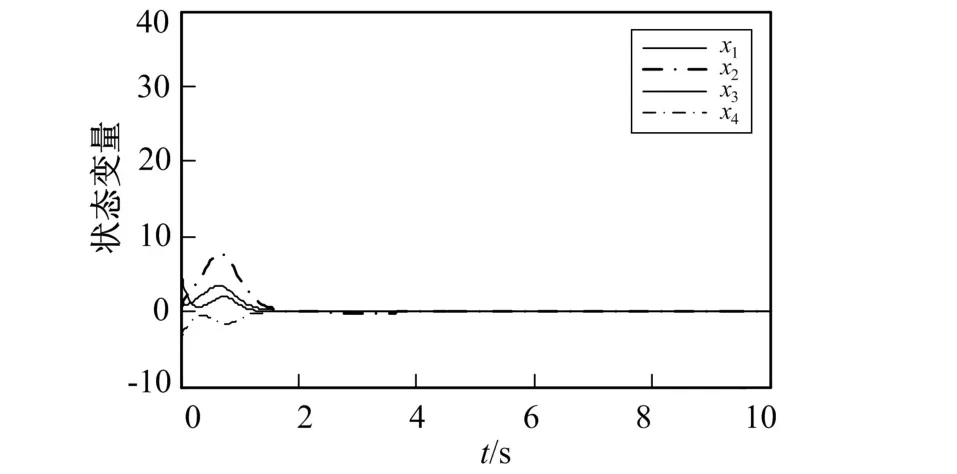
图4 带扰动分数阶超混沌Lorenz系统的状态变量随时间变化图Fig.4 The state variables of disturbed fractional order hyperchaotic Lorenz systems

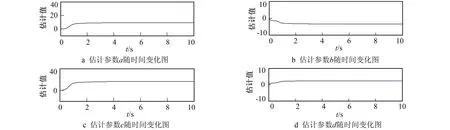
图5 带扰动系统的估计参数随时间变化图Fig.5 The time variations of the estimated parameters of the disturbed systems

4 结 语

笔者基于分数阶微积分引理及有限时间Lyapunov原理,通过设计控制器及自适应法则实现了带有未知参数的分数阶超混沌Lorenz系统的有限时间控制问题。该方法简单有效,可使系统的状态变量在有限时间内收敛到平衡点,收敛速度较快,具有良好的鲁棒性能。数值仿真验证了该控制的有效性及准确性。

[1]MOHAMMAD POURMAHMOOD AGHABABA.Fractional Modeling and Control of a Complex Nonlinear Energy Supply-Demand System[J].Complexity,2015,20(6):74-86.

[2]PODLUBNY I.Fractional Differential Equations[M].New York:Academic Press,1999.

[3]BEHINFARAZ R,BADAMCHIZADEH M A,GHIASI A R.An Approach to Achieve Modified Projective Synchronization between Different Types of Fractional-Order Chaotic Systems with Time-Varying Delays[DB/OL].(2015-07-08).[2017-03-08].https:∥doi.org/10.1016/j.chaos.2015.07.008.

[4]RAYNAUD H F.State-Space Representation for Fractional Order Controllers[J].Automatica,2000,36(7):1017-1021.

[5]BEHINFARAZ R,BADAMCHIZADEH M A.Synchronization of Different Fractional-Ordered Chaotic Systems Using Optimized Active Control[C]∥IEEE International Conference on Modeling,Simulation,and Applied Optimization.[S.l.]:IEEE,2015:1-6.

[6]SONG X.Output Feedback Control for Fractional-Order Takagi-Sugeno Fuzzy Systems with Unmeasurable Premise Variables[J].Transactions of the Institute of Measurement&Control,2015,38(10):1201-1211.

[7]YIN C,DADRASS,ZHONG SM,et al.Control of a Novel Class of Fractional-Order Chaotic Systems via Adaptive Sliding Mode Control Approach[J].Applied Mathematical Modelling,2013,37(4):2469-2483.

[8]CHEN D Y,LIU Y X,MA X Y,et al.Control of a Class of Fractional-Order Chaotic Systems via Sliding Mode[J].Nonlinear Dynamics,2011,67(1):893-901.

[9]AGHABABA M P.A Novel Terminal Sliding Mode Controller for a Class of Non-Autonomous Fractional-Order Systems[J].Nonlinear Dynamics,2013,73(1/2):679-688.

[10]KAMENKOV G V.On Stability of Motion over a Finite Interval of Time[J].Akad Nauk Sssr Prikl Mat Meh,1953(4):529-540.

[11]BHAT SP.Continuous Finite-Time Stabilization of the Translational and Rotational Double Integrators[J].IEEE Transactions on Automatic Control,1998,43(5):678-682.

[12]AMATO FRANCESCO.Finite-Time Stability of Linear Time-Varying Systems:Analysis and Controller Design[J].IEEE Transactions on Automatic Control,2010,55(4):1003-1008.

[13]GARCIA.Finite-Time Stabilization of Linear Time-Varying Continuous Systems[J].Automatic Control,2009,54(2):364-369.

[14]LAZAREVIC'M P.Finite Time Stability Analysis of Linear Autonomous Fractional Order Systems with Delayed State[J].Asian Journal of Control,2010,7(4):440-447.

[15]LAZAREVIC'M P.Finite Time Stability Analysis of PDA Fractional Control of Robotic Time-Delay Systems[J].Mechanics Research Communications,2006,33(2):269-279.

[16]WANG J,GAO T,ZHANG G.Adaptive Finite-Time Control for Hyperchaotic Lorenz-Stenflo Systems[J].Physica Scripta,2015,90(2):25204-25208.

[17]KILBASA A,SRIVASTAVA H M,TRUJILLO J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam:Elsevier,2006.

[18]ZHAO Y,WANG Y,LIU Z.Finite Time Stability Analysis for Nonlinear Fractional Order Differential Systems[C]∥IEEE Control Conference.[S.l.]:IEEE,2013:487-492.

[19]李雄.分数阶非线性系统稳定性分析及同步控制[D].西安:陕西师范大学数学与信息科学学院,2016.LI Xiong.Stability Analysis and Synchronization Control of Fractional Order Nonlinear Systems[D].Xi'an:School of Mathematics and Information Science,Shanxi Normal University,2016.

[20]LI Y,CHEN Y Q,PODLUBNY I.Stability of Fractional-Order Nonlinear Dynamic Systems:Lyapunov Direct Method and Generalized Mittag-Leffler Stability[J].Computers&Mathematics with Applications,2010,59(5):1810-1821.

[21]NORELYSAGUILA-CAMACHO.Lyapunov Functions for Fractional Order Systems[J].Communications in Nonlinear Science&Numerical Simulation,2014,19(9):2951-2957.

[22]BECKENBACH E F,BELLMAN R.Inequalities[J].Ergebnisse der Mathematik und ihrer Grenzgebiete,1962,42(9):421-422.