基于节点相似度的社团划分方法研究∗

甘立强 王旭阳 燕 楠 王 岚

（1.中国科学院深圳先进技术研究院中国科学院人机智能协同系统重点实验室 深圳 518055）（2.兰州理工大学计算机与通信学院 兰州 730050）

1 引言

近年来复杂网络已经得到了广泛的应用，如万维网、社会网、蛋白质交互网以及科学家合作关系网等。这些网络具有较高的复杂性，因此被称为“复杂网络”［1］。复杂网络已经成为当前最重要的多学科交叉研究领域之一［2］。随着对复杂网络性质的物理意义和数学特性的深入研究，人们发现许多复杂网络都具有一个共同的性质，即社团结构［3］。社团内部各节点之间连接紧密，而不同社团节点之间连接稀疏。社团结构分析在生物学、物理学、计算机图形学和社会学等领域内有着广泛的应用。

目前，学者们已经提出了很多有效的社团检测方法，比如基于分裂思想的GN算法［4］，自包含GN算法［5］、基于相异性的分裂算法［6］。该类算法划分效果较好，但是时间复杂度太高，不适合在大型网络中使用，随后学者们根据上述缺点提出了基于凝聚 思 想 的 Newman 快 速 算 法［7］、CNM 算 法［8］、MSG-VM［9］，但是这些算法容易将过多的节点划分到同一社团，导致社团过大，与真实网络的划分情况不相符。因此，针对这些缺点学者们又相继提出了 LPAm 算法［10］、SYM［11］、CHM［12］、ILM［13］等，这些算法同样存在很多问题，诸如LPAm算法的稳定性不高，时间复杂度虽然较小，但是不容易得到最优结果，CHM算法空间复杂度高，需要较大的内存空间，不适合大型网络，ILM算法参数选择困难，算法稳定性差等。

针对上述存在的问题，通过比较研究各种网络节点相似度的构造方法，通过综合考虑网络的局部信息和全局信息，设计了新的构造节点相似度的方法，进而提出了基于节点相似度的社团划分算法。该算法在不需要知道任何关于网络的先验知识的情况下，仍然取得了较好的划分结果。

2 基本概念

2.1 节点相似度

构造节点相似度方法目前主要是基于网络的局部信息［14］，比如 Salto［15］、Jaccard［16］、Hub Pr-omot⁃ed［17］、Leicht-Holme-Newman［18］、RA［19］等。其中 RA方法是目前效果最好的节点相似度的构造方法［19］。

RA方法是通过模拟网络中资源的分配过程来衡量两个节点的相似度。假设有一个节点对（i，j），节点 j通过它们的共同邻居节点作为中介间接地向节点i发送一定资源。同时规定每个中介能拥有的资源是一定的。因此每个中介发送给节点i的资源取决于它的度。资源分配过程如图1，我们可以把节点i收到节点 j发送的资源的多少定义为节点i和节点 j的相似度：

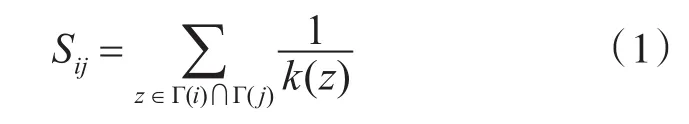
其中，Γ(i)代表节点i的所有邻居节点的集合，z∈Γ(i)∩Γ(j)代表节点i和节点 j共同邻居节点的集合，k(z)代表节点z的度。

但是这种只是依靠网络的局部信息作为衡量相似度的标准容易过度追求局部最优，忽视了网络整体的结构，造成与实际网络不符的情况，例如将RA算法应用在经典的Zachary空手道俱乐部网络中，按照式（1）计算节点之间的相似度，发现节点3对应的最大相似度节点是节点34，应该被分到同一个社团中，但是现实网络中它们被分到了以教练和主管为首的两个社团中。所以划分社团中应该考虑网络的全局拓扑信息。如果两个节点的距离越近，即它们之间的最短路径越短，这两个节点同属于一个社团的机会就越大，反之，则它们属于一个社团的机会就越小［20］。因此综合两个节点间共同邻居的网络局部信息和节点间最短路径的网络全局信息，本文重新定义了节点相似度Sim(i，j)：

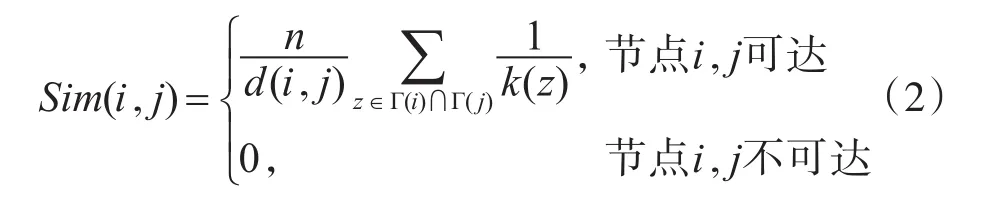
其中d(i，j)表示节点i和节点 j之间最短路径长度，n代表网络中的节点数目，节点i，j可达是指节点i，j之间存在路径将其连通。当d(i，j)越小时，1 d(i，j)越大，则 Sim(i，j)就越大，两个节点越相似。同时如果两个节点之间没有可以到达的路径，这说明这两个节点之间的资源交换主要依靠邻居节点，相对于直接相连的节点，交换的资源较少，可以忽略。因此我们把相似度设置为0。因为Si，j本身很小，再除以d(i，j)结果可能小到超出计算机的表示范围，就会出现浮点数下溢出的情况，将该运算结果处理成机器零，这时就无法对相似度进行比较。所以乘以n对结果进行适当的放大，防止这种情况发生。

图1 网络资源流动过程图

2.2 模块度和准确率

社团模块度［20］是Newman等引进的一个衡量网络划分质量的度量标准。假设有某种划分形式，将网络划分为k个社团，定义一个k×k维的对称矩阵E=(eij)，其中eij表示网络中连接两个不同社团的节点的边在所有边中所占的比例，这两个节点分别位于第i和第 j个社团。模块度Q可表示为

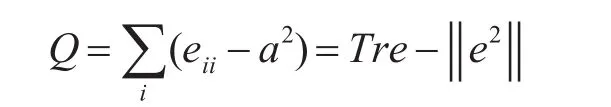
3 基于节点相似度的社团划分方法

3.1 基本思想

两个节点的相似度越大，属于同一个社团的概率越大［21］，根据这一思想，本算法利用节点之间的相似性，判断两个节点是否属于同一个社团。

对于一个含有n个节点的网络，首先根据式（2）计算网络中所有节点对的相似度。由此我们可以得到一个 n×n的矩阵 Sim(n，n)=[ ]Sim(i，j) 。Sim(i，j)代表的是两个节点之间的相似度。为了方便处理数据，我们把这个矩阵的每一行用链表存起来，头节点保存节点i，头节点的next节点保存节点i对应的相似度最大的节点 j。如果有多个相似度相同的节点，则把它们都保存起来。算法具体步骤：

1）首先将每个节点看作是一个社团，选择任意一个节点作为初始节点；

2）然后从剩余的节点中选择和这个节点相似度最大的节点，将它们合并成一个新的社团；

3）最后再将新加入的节点作为初始节点，寻找和它相似度最大的节点。如果找到的这个节点不在当前的社团中，则把这个节点合并到当前社团，如果在的话，就随机从剩余未处理的节点中选择一个作为初始节点，回到2）；

4）重复执行步骤2）和3），直到处理完所有的节点。

为了更清楚地表达本文算法的思想，我们构建了一个含有8个节点的小网络（如图2）。

首先计算每个节点和它邻居节点的节点相似度，然后找出每个节点以及它对应的相似度最大的节点（结果如表1）。

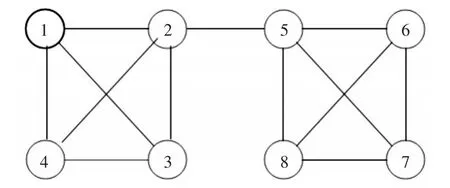
图2 示例网络

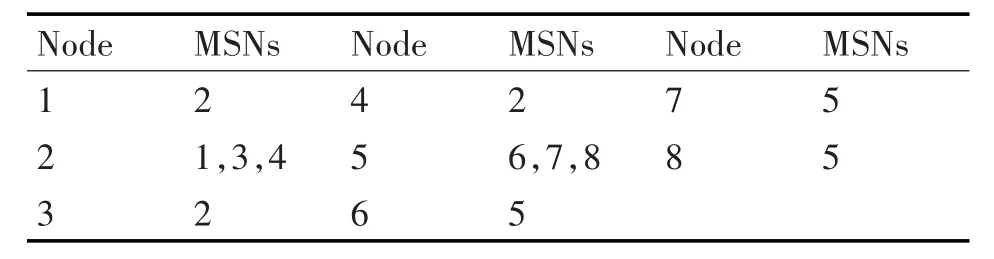
表1 对应的最大相似度节点列表

然后随机地选择一个节点，用带箭头的线段将当前节点和对应的相似度最大的节点连接起来，箭头指向的是对应的相似度最大的节点。同时，线段两端的节点合并到同一个网络。等到标记完网络中所有的节点，划分过程结束，得到最后的划分结果（如图3）。

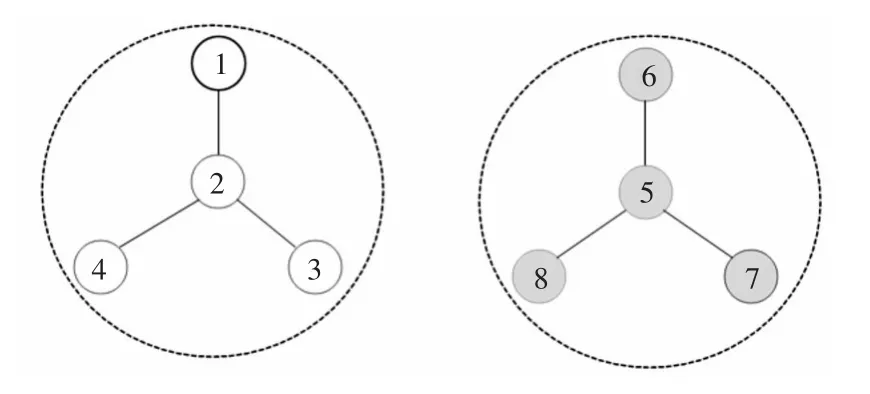
图3 本文算法划分结果

针对上述步骤，有一种特殊情况需要说明，如果一个节点和它所有的邻居节点都没有共同的邻居节点，则这个节点和其它所有节点的相似度都等于0，因此按照上述算法无法完成划分，这种情况下我们把这个节点划分到它邻居节点中度最大的那个节点所在的社团中。因为一个节点的度越大，它就越重要，新来的节点就倾向于和这个节点靠拢［22］。同时为了进一步提高划分社团的准确率，我们引进一个相似度阈值ε，当一个节点和它所有邻居节点的最大相似度小于ε时，我们就把这个具有最大相似度的节点划分到它所有邻居节点中度最大节点所在的社团中，因为如果相似度很小，依然使用节点的这个属性作为划分标准的话，容易过拟合。针对不同的网络这个ε也不同，我们可以通过调整ε的值来获得更好的划分效果。

3.2 算法性能分析

本算法需要时间的步骤主要包括三部分：计算节点相似度，寻找下一个需要处理的节点，合并社团。由于下一个要处理的节点是当前节点对应的相似度最大的节点，并且之前我们已经把这两个节点存在一个以当前节点为头节点的链表中，因此可以直接获取到下一个需要处理的节点，因此这部分的计算时间可以忽略。计算节点相似度只需要知道它最近的邻居节点的信息，因此计算量非常小。计算式（2）的时间复杂度是O()1，计算一个节点和它的k个邻居节点相似度的时间复杂度就是O(k)，k是网络中节点的平均的度。因此计算有n个节点的网络所需要的时间复杂度为O(kn)。合并一个节点和它相似度的节点所需要的时间复杂度明显的是O(1)。所以将网络中所有n个节点都合并花费的时间复杂度是O(n)。使用Dijkstra算法计算网络中节点之间的最短路径的时间复杂度为O(n2)，所以算法时间复杂度为O(k+n)n≈O(n2)(k＜＜n)。而CHM、ILM算法的时间复杂度也同样为O(n2)。

4 实验结果与分析

4.1 Zachary空手道俱乐部网络

空手道俱乐部网络是描述美国一所大学里空手道俱乐部里俱乐部成员之间关系的网络［23］，该网络由Zachary耗时两年研究出来的。此网络含有34个节点和78条边，节点表示俱乐部中的成员，边表示俱乐部成员之间的关系。通过研究发现，由于俱乐部主管JohnA（node 34）和俱乐部教练员Mr.Hi（node 1）之间产生分歧，俱乐部被划分成了以主管和教练为首的两个团体。首先通过式（2）计算每个节点的和邻居节点的相似度，然后找出最大相似度的节点，结果如表2。然后用本文算法对其进行划分，图4描述了此次划分的过程（ε=0.88）。由结果可以看出本文算法划分的结果与现实中的划分结果一致。

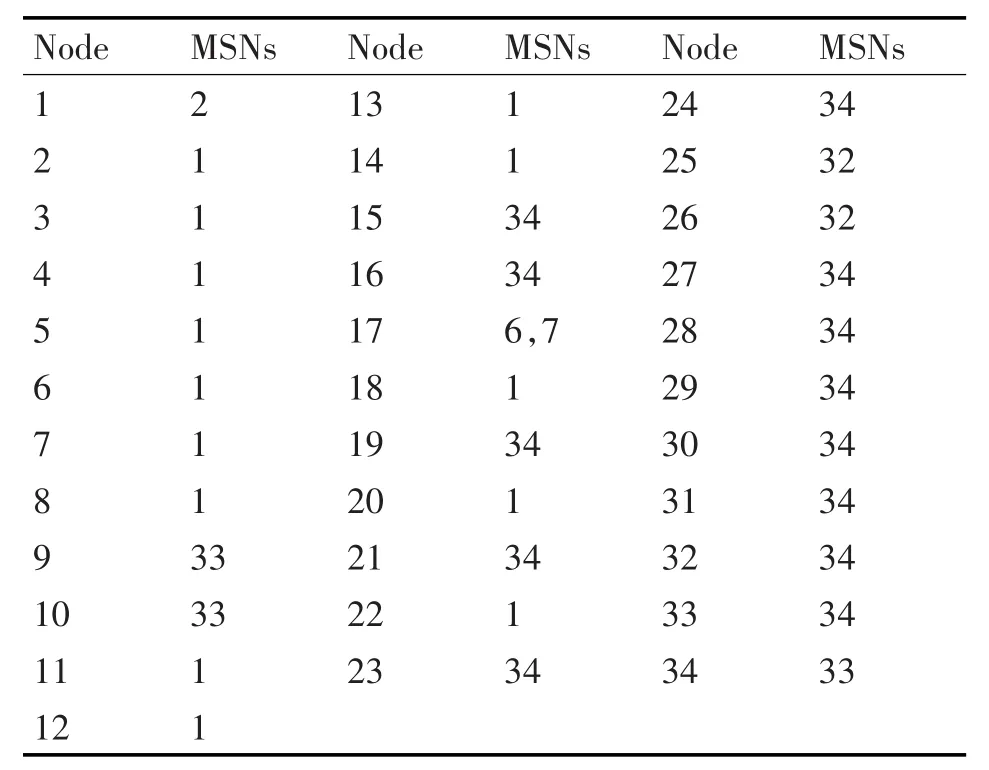
表2 Zachary网络中对应的最大相似度节点列表

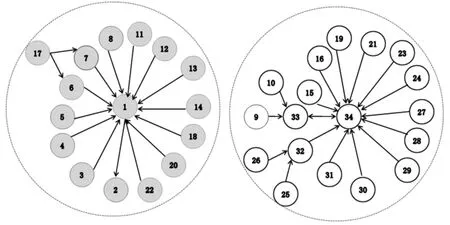
图4 Zachary网络的划分过程

表3表示将本文算法与Newman快速算法和CNM算法进行比较，通过结果可以看出本文算法模块度更大，准确率更高，因此本文算法更适合划分Zachary空手道俱乐部网络。

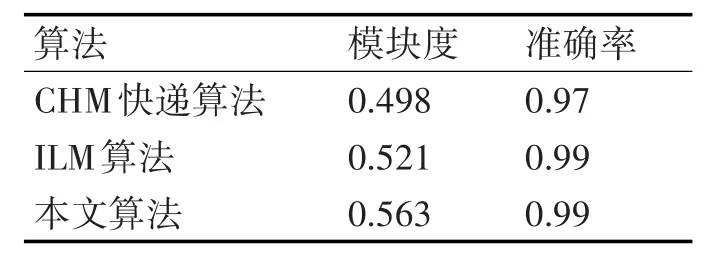
表3 不同算法的性能比较

4.2 美国大学足球赛网络

美国大学足球赛网络［24］由115个节点613条边组成。每个节点代表一支球队，每条边代表端点上的两支队伍进行过比赛。这些球队被划分成若干个小组，每个小组有8～12名球员，同组内球队进行比赛的次数要比组间球队之间比赛的次数多。如图5（ε=0.7）所示本文算法将网络划分11个社团，其中7个社团和现实网络中的社团一致，但是CNM算法只划分出7个社团，其中划分完全正确的社团只有4个。所以本文提出的算法划分社团的准确率更高。表4表示的是本文算法与Newman快速和CNM算法的从模块度和准确率上对比的结果，从数据上看，本文算法要优于Newman快速算法和CNM算法。

图5 美国大学足球赛网络

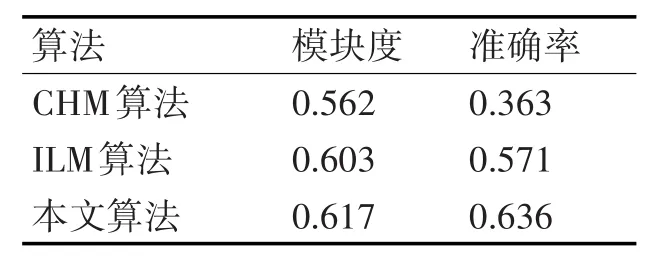
表4 不同算法性能比较

4.3 海豚社会网络

Lusseau等在新西兰对62只宽吻海豚的生活习性进行了长时间的观察，他们研究发现这些海豚的交往呈现出特定的模式，并构造了包含有62个结点的社会网络［25］。如果某两只海豚经常一起频繁活动，那么网络中相应的两个结点之间就会有一条边存在。利用本算法划分的结果如图6（ε=0.75）所示。从图6可以看出，本文算法划分的结果与现实中的划分较为符合。

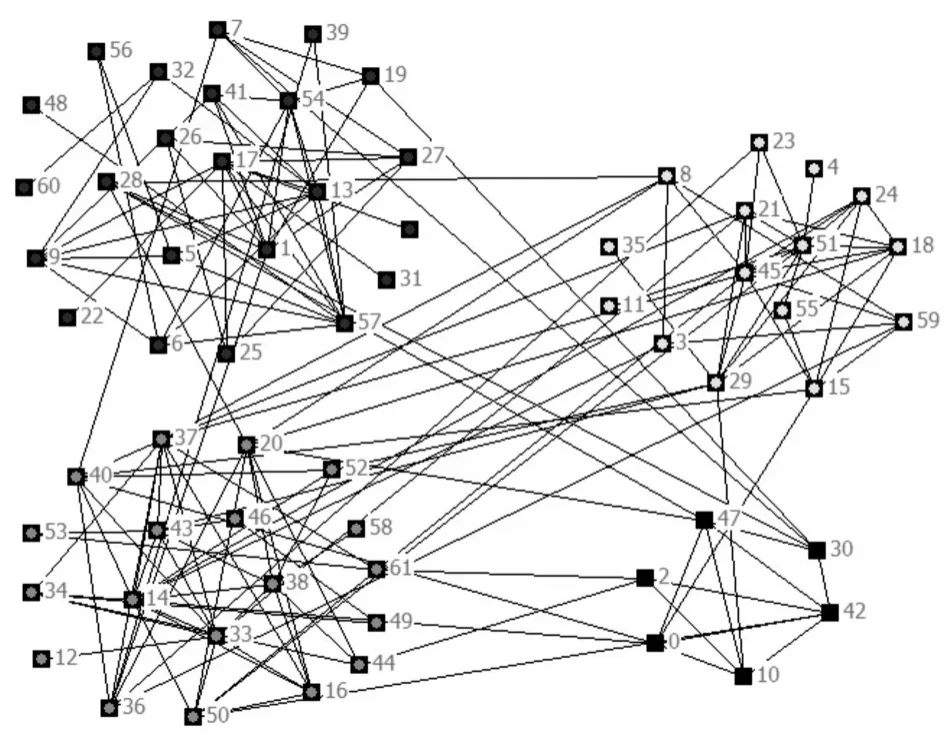
图6 海豚社会网络

5 结语

目前节点相似度的构造方法大多数是基于网络的局部信息，使用这种构造方法的节点相似度容易使算法陷入局部最优，使得划分结果和真实网络差异较大，针对这一缺点，本文综合网络局部信息和全局信息，重新定义了节点相似度，并设计了基于凝聚思想的划分算法，通过与CHM算法、ILM算法的对比，在时间复杂度相当的情况下，经过仿真实验证明，本文算法可以更好地对复杂网络进行划分。因此，可以将本文算法用于复杂网络中的社团划分。

［1］骆志刚，丁凡，蒋晓舟.复杂网络社团发现算法研究新进展［J］.国防科技大学学报，2011，33（1）：47-52.

LUO Zhigang，DING Fan，JANG Xiaozhou.New Progress on Community Detection in Complex Networks［J］.Journal of National University of Defense Technology，2011，33（1）：47-52.

XIE Zhou，WANG Xiaofan.An Overview of Algorithm for Analyzing Community Structure in Complex Networks［J］.Complex Systems and Complexity Science，2005，2（3）：1-12.

［3］Chen Y，Wang X，Bu J，et al.Network structure explora⁃tion in networks with node attributes［J］.Physica A：Sta⁃tistical Mechanics and its Applications，2016，449：240-253.

［4］Guimera R，Danon L，Diaz-Guilera A，et al.Self-similar community structure in a network of human interactions［J］.Physical review E，2003，68（6）：065103.

［5］Radicchi F，Castellano C，Cecconi F，et al.Defining and identifying communities in networks［J］.Proceedings of the National Academy of Sciences of the United States of America，2004，101（9）：2658-2663.

［6］Zhou H.Distance，dissimilarity index，and network com⁃munity structure［J］.Physical review e，2003，67（6）：061901.

［7］Newman M E J.Detecting community structure in networks［J］.European Physical Journal B，2004，38（2）：321-330.

［8］Clauset A.Finding local community structure in networks［J］.Physical Review E，2005，72（2）：26-132.

［9］Schuetz P，Caflisch A.Efficient modularity optimization by multistep greedy algorithm and vertex mover refinement［J］.Physical Review E，2008，77（4）：046112.

［10］Frey B J，Dueck D.Clustering by passing messages be⁃tween data points［J］.Science，2007，315：972-976.

［11］Symeonidis P，Tiakas E，Manolopoulos Y.Transitive node similarity for link prediction in social networks with positive and negative links［C］//Pro-cedings of the fourth ACM conference on Recommendersystems.ACM，2010：183-190.

［12］H.Chen，L.Guo，X.L.Zhang，C.L.Giles，Proceedings of the 27th Annual ACM Symposium on Applied Comput⁃ing［J］.2012，1：138-143.

［13］Li Y，Luo P，Wu C.Information loss method to measure node similarity in networks［J］.Physica A：Statistical Mechanics and its Applications，2014，410：439-449.

［14］Chen Z，Xie Z，Zhang Q.Community detection based on local topological information and its application in power grid［J］.Neurocomputing，2015，170：384-392.

［15］Salton G，McGill M J.Introduction to modern informa⁃tion retrieval［J］.1986.

［16］Jaccard P.Etude comparative de la distribution florale dans une portion des Alpes et du Jura［M］.Impr.Corbaz，1901.

［17］Ravasz E，Somera A L，Mongru D A，et al.Hierarchical organization of modularity in metabolic networks［J］.sci⁃ence，2002，297（5586）：1551-1555.

［18］Leicht E A，Holme P，Newman M E J.Vertex similarity in networks［J］.Physical Review E，2006，73（2）：026120.

［19］Zhou T，Lü L，Zhang Y C.Predicting missing links via local information［J］.The European Physical Journal B-Condensed Matter and Complex Systems，2009，71（4）：623-630.

［20］Liu J G，Zhou T，Che H A，et al.Effects of high-order correlations on personalized recommendations for bipar⁃tite networks［J］.Physica A：Statistical Mechanics and its Applications，2010，389（4）：881-886.

［21］Symeonidis P，Tiakas E，Manolopoulos Y.Transitive node similarity for link prediction in social networks with positive and negative links［C］//Proceedings of the fourth ACM conference on Recommender systems.ACM，2010：183-190.

［22］Barabási A L，Albert R.Emergence of scalling in ran⁃dom networks［J］.Science，1999，286（5439）：509-512.

［23］Zachary W W.An information flow model for conflict and fission in small groups［J］.Journal of anthropological re⁃search，1977，33（4）：452-473.

［24］Girvan M，Newman M E J.Community structure in so⁃cial and biological networks［J］.Proceedings of the na⁃tional academy of sciences，2002，99（12）：7821-7826.

［25］Barabási A L，Albert R.Emergence of scaling in random networks［J］.science，1999，286（5439）：509-512.