一种新型启发式PSO算法求解市区最优路径规划研究∗

方 昕

（安康学院电子与信息工程学院 安康 725000）

1 引言

在GIS路网分析中经常会遇到优化问题，其中路径寻优是核心问题之一。路径寻优是在路网环境里按照一定指标如最短路径、最小耗时、最少耗费、最少转向等，搜索一条从起点到终点的最短路径或最优路径［1］。求解路径的方法总体上分为传统算法和智能算法两类。传统算法有深度优先、广度优先、图搜索、自由空间法、A*算法［2］等，其存在效率低、耗时长、存储大等不足。智能算法有粒子群算法［3］、蚁群算法［4］、遗传算法、鱼群算法等，其具有效率高、易实现等优点。其中，启发式算法既可为传统算法又可为智能算法，是根据初始化解对其不断优化最终找到近似最优解，可在不耗费大量资源的前提下，利用启发信息快速求解路径问题。在智能算法中，粒子群算法即属于启发式算法的一种，在初始化粒子群体时给粒子个体添加启发信息即可引导粒子前行。

粒子群优化算法（PSO）是Kennedy和Eberhart于 1995年提出的新型智能优化算法［5～6］，其基本思想是：每个粒子位置在搜索空间中代表一个可行解，所有粒子通过目标函数决定其适应值。每个粒子速度决定粒子的飞行方向与距离，通过不断更新迭代最终找到评价最优的函数值即最优解。与其他算法相比，粒子群算法具有简单、易实现、收敛速度快、参数少、应用广等优点，并适用于复杂非线性问题及离散优化问题。但PSO算法也是一种随机启发式算法，其自身存在一些不足，如局部搜索能力差、速度和位置更新公式不完善、初始化粒子随机性强等问题，严重影响了路径规划的寻优效率和可靠性。

在对其深入研究中，国内外学者提出了各种改进方法，如张万绪［7］等提出一种惯性权重的调整方法改进粒子群算法，同时引入安全度和平滑度概念完成机器人路径规划；张铁虎［8］等建立了点胶机路径规划模型，将蚁群算法和粒子群算法相结合求解TSP问题；变异增加群体多样性求解TSP问题。

孙凯［12］等利用粒子群算法优化蚁群参数来求解TSP问题；朱莹莹［13］等将粒子群与遗传算法相结合，引入遗传中的交叉、学习因子或与其他算法相结合等思想引入到了PSO算法中，从而兼顾粒子群多样性和收敛速度两方面的性能。

本文受到了上述启示来求解市区最优路径问题，将A*算法思想引入到离散PSO算法中，采用新的启发函数初始化粒子群体，引入非线性动态调整算法惯性权重和平滑度概念，提出一种新型启发式PSO算法，双重提高算法性能，增强粒子群体后期全局搜索能力，抑制群体陷入局部极值。该算法在求解最优路径时，首先根据市区地图数据信息利用数学推导建立平面路网环境模型，在此基础上利用启发函数、惯性权重调整、平滑度不断迭代更新群体最优解，从而保证算法的精度、效率、收敛性。

2 市区路网的算法模型

标准的粒子群算法（Particle Swarm Optimiza⁃tion，PSO）来源于鸟类觅食行为，于1995年由Ken⁃nedy、Eberhart博士提出的群智能算法［5～6］。算法采用速度-位置搜索模型，将每只鸟抽象化描述转化为粒子，用随机解初始化一群随机粒子，粒子在搜索空间中有自身的速度引导其飞行，通过迭代逐渐向目标区域靠近，在每次迭代中，每个粒子通过更新个体极值和全局极值来更新自己，不断调整自己的速度和位置。在PSO算法中，每个个体都被看成搜索空间中无体积无质量的粒子，每个粒子以一定速度飞行。此飞行速度会随着全体粒子群飞行状况即全局最优状况和粒子自身飞行状况即局部最优状况做调整。而标准的PSO算法是针对连续优化问题提出，与本文的最优路径问题截然不同。要求解本文的最优路径问题必须将标准PSO算法进行离散化处理，搭建路网模型。

本文以Clerc［14］提出定义PSO算法数学对象与运算规则为依据重新定义了求解市区路网的最优路径问题的算法整数序规范。算法可描述为：设在D维搜索空间中有m个粒子，第i个粒子可用向量表示为 xi=(xi1，xi2，xi3，…，xiD)，其中每个 xi都有整数编码，每个编码都是地图数据中地理坐标推导后的节点。每个粒子好坏通过粒子权重值与目标函数值比较而得到。即市区路网节点的经度与纬度数据通过空间投影将坐标换算为平面节点坐标（x，y）值，于是可知搜索空间的n个节点平面坐标。利用数学方法可求取任意节点间距离，其中地球半径为6371229.0m。这样粒子目标使已知市区内n个节点坐标，寻找一条整数序列 x={c1，c2，…cn}，使得x上的权重值最小，ci代表位置i对应的编码［15］。粒子目标函数 F(x)为

式中：F(x)这里表示为路径的权重值即距离长度或适应度值，d(ci，cj)表示ci与cj两节点间距离，i，j∈[1，n]。

在每次计算粒子目标函数值后还需利用式（2）来判定粒子好坏：

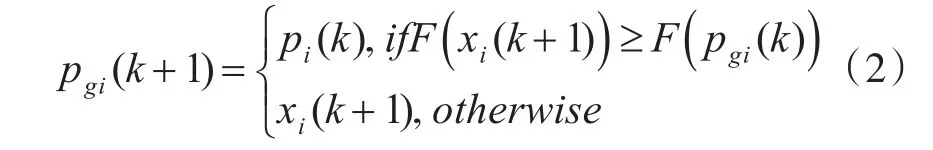
式中，pi(k)代表粒子自身当前第k次迭代的最好位置，pgi(k)代表粒子群体的最好位置。如果此时达到目标函数值或最大迭代次数，则输出当前群体最优路径 pgi和路径长度F(pgi)。

粒子寻优过程中粒子速度表示为vi=(vi1，vi2，vi3，…，viD)。第i个粒子在搜索空间中最好位置为pi=(pi1，pi2，pi3，…，piD)，粒子群体中最好位置为pg=(pg1，pg2，…，pgm)。这m个粒子群体在每次比较产生目标函数值后都会根据式（3）进行粒子位置和速度的更新，从而产生新的粒子和速度［15］。

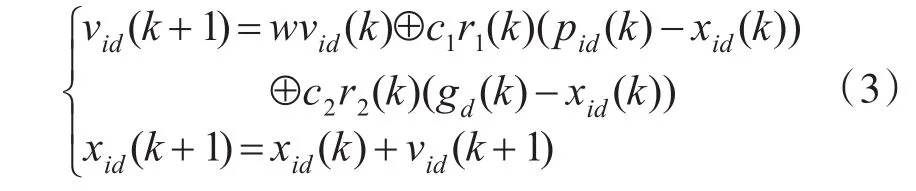
式中，1≤i≤m，1≤d≤D ，w 是惯性权重，c1和c2是加速因子，k表示第k次迭代，r1和r2都属于［0，1］上的随机数，wvid代表粒子个体保留本身速度的能力，“-”表示粒子位置相减为一系列节点交换集，“⊕”表示交叉二元运算组成有序交换集，“+”表示位置与速度相加成为新的粒子位置。在计算过程中，c1r1(pid-xid)代表粒子在第k次迭代时的(pid-xid)速度保留概率，c1r1越大则(pid-xid)中速度保留概率就越大，说明粒子自身具有很强的局部搜索能力；c2r2(gd-xid)代表粒子在第k次迭代时的(gd-xid)速度的保留概率，c2r2越大则(gd-xid)中速度的保留概率就越大，说明粒子群体具有很好的全局搜索能力。从上面计算式子可看出，PSO算法易于计算机编程实现，各个粒子的速度和位置相对独立，同时还保存着相对微妙的联系组成群体全局最优解。随着粒子个数、粒子初始位置、速度、目标函数的不同，群体的解也会不同［15］。

因此，通过调节惯性权重或随机数就能调整算法的全局与局部搜索能力，但粒子群算法存在随机初始化概率大、局部搜索能力弱等不足，导致运算结果不稳定。而A*算法是经典启发式搜索算法，可在初始化种群时通过计算评价函数初始化粒子，降低其初始化随机概率。为此，本文拟结合这两种算法的优势，将两种算法进行深层次融合，进而提出一种求解市区路网最优路径的新型的启发式PSO算法。

3 新型的启发式PSO算法

粒子群算法在环境模型中寻找最优路径时，每个粒子都代表一个解即有效路径，但有效路径并不代表最优路径，在每次粒子迭代更新时都需要从粒子中寻找当前的最优解，粒子优化目标函数即为粒子所代表的路径长度，在算法模型中指每个粒子的权重值。

3.1 改进初始化粒子

在初始化m个粒子时先利用A*算法的思想计算评价函数（如式（4））。

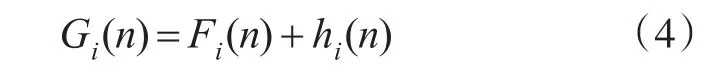
其中，Gi(n)代表第i个粒子中从起点经由扩展点n到达终点的耗费；Fi(n)代表第i个粒子中起点到扩展点n的实际耗费，由式（1）演变得到；hi(n)代表第i个粒子中扩展点n到终点的估价值，保持不变。当hi(n)总小于等于从n点到终点的实际耗费时，能保证找到最优解。本文hi(n)主要指路径长度可由式（5）表示：

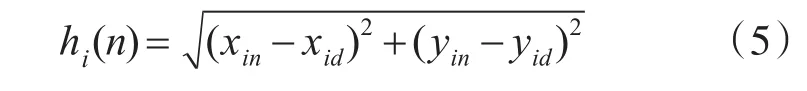
式中，hi(n)表示第i个粒子中扩展节点n到终点的直线距离，(xin，yin)表示粒子扩展节点n的坐标，(xid，yid)表示粒子终点的坐标。

3.2 引入平滑度

由于评价函数会促使算法在进行路径寻优时会选取对角线以便缩短路径长度及运行时间，为此在搜索过程中引入平滑度。平滑度：设置路径存储置OPEN表和CLOSED表。CLOSED表存储从起点开始的路径节点，最终保存每个粒子从起点到终点的最优路径；OPEN表保存CLOSED表中粒子搜索的当前节点的后续节点，不保存已扩展其他节点的后续节点，节点间的评价函数计算保持不变，路径长度越小代表与目标越靠近。

Step1：首先设置变量i初始值为0，平滑度计算开始。

Step2：判断粒子的CLOSED表的第i+1个节点是否为终点D，如果是则处理结束；否则，转入Step3。

Step3：判断粒子中第i个节点与第i+2个节点是否直通，如果是则转入Step4；否则转入Step5。

Step4：删除粒子的CLOSED表中第i+1个节点，转入Step5。

Step5：计数 i自增1，转入Step2。

3.3 调整惯性权重

针对粒子群算法易陷入局部最优、早熟收敛导致迭代后期搜索能力下降的缺点，从惯性权重会影响粒子搜索速度和搜索能力考虑调整粒子迭代过程中的惯性权重，改进粒子群算法。惯性权重计算公式如下

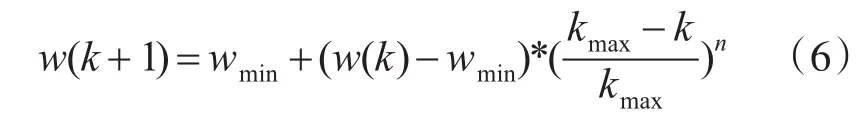
式中，kmax表示最大迭代次数；w表示当前第k代粒子的惯性权重，初始化值为wmax；w(k+1)表示随初始值及迭代变化w(k)的值呈非线性下降。当粒子在迭代过程中远离目标区域时，n值调大w值此时较大，使得w下降速度减慢，粒子能较快地飞向群体最优位置；当粒子靠近目标区域时，n值调小w值此时变小，使得w下降速度加快，粒子能在目标区域中进行更细致的搜索，以便搜索到群体最优值，从而更新群体全局最优解，即更新公式调整为

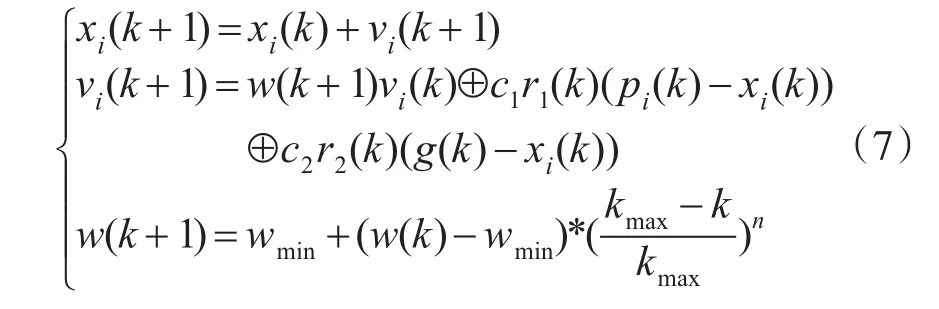
其中，粒子在二维环境模型中搜索，1≤i≤m。

3.4 算法流程

新型的算法综合考虑了算法的初始化、收敛速度，不仅从基本粒子群算法上进行改进，而且算法融入了启发函数、平滑度、惯性权重调整，在算法模型中进行测试，新型的算法无论在运行速度、收敛精度上都有较大提高。算法实现步骤如下：

Step1：初始化种群。初始化m个粒子，粒子速度，迭代次数，适应度值。同时，创建OPEN表和CLOSED表。

Step2：计算粒子适应度值。根据式（1）计算每个粒子适应值。将最初的适应度值作为粒子的当前最优值 pi(k)，按照式（2）评价粒子好坏并求解pg(k)。

图1 改进算法流程图

Step3：判断是否符合结束条件或终点D是否在CLOSED表中。如果是则转到Step7，否则进入Step4。

Step4：引入平滑度，CLOSED表中选取节点扩展，将扩展节点的后续节点加入清空的OPEN表中。再次判断终点D是否在表中，是则输出结果，否则转入Step5。

Step5：计算粒子适应度值并评价粒子。

Step6：调整惯性权重，更新粒子群体。按式（7）更新粒子速度和位置，产生新一代粒子。

Step7：判断是否符合结束条件。如果是则算法结束，输出结果，否则转到Step4。

结束条件：达到规定的粒子迭代次数或预定目标函数值。

4 实例仿真分析

本系统采用某市区的地图数据，通过地理坐标空间投影构成带权图G，图中有用节点个数共计16，并以此编号，节点边数为35。新型的算法在Vi⁃sual Studio2005.net环境下用VC++编程实现，为了更好统计算法性能，将规划路径、路径长度和运行时间作为参考，并与PSO算法，A*算法结果进行比较，其中粒子最大速度vmax=15，c1=c2=2，r1=r2=0.5，R=0.2，最大惯性权重wmax=0.9，最小惯性权重wmin=0.4。为了验证算法的有效性，实验中粒子群算法的迭代次数取50、100、200，粒子个数取20、30、50、100、200，然后求解每组迭代下的平均解和最优解、平均耗时，统计各个算法搜索结果如图3、表1所示。

硬件环境：Intel（R）Core（TM）2 CPU 6320；

操作系统：Microsoft Windows；

软件环境：Visual Studio。

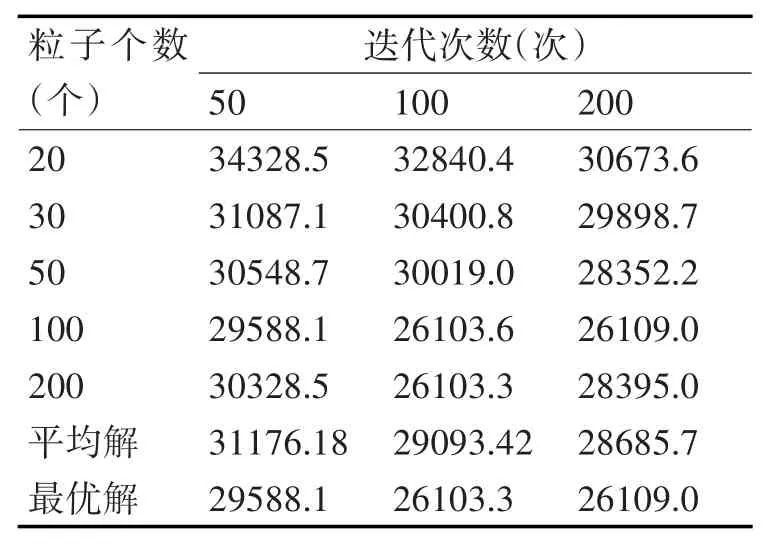
表1 新型算法结果统计

从表1中可看出新型算法能有效求解最优路径问题，且随着迭代次数和粒子个数不断增加的情况下，粒子的权重值将逐渐减小。当粒子个数增大到200时，粒子求解的路径长度反而变大，可见粒子群算法中根据求解的问题设置合适的参数对求解结果有较大影响，此处粒子个数设置为100较为理想，平均解也较好。因此在进行下述算法比较时，粒子个数取100，迭代次数依次取50、100、200。算法结果统计如表2、图2所示。

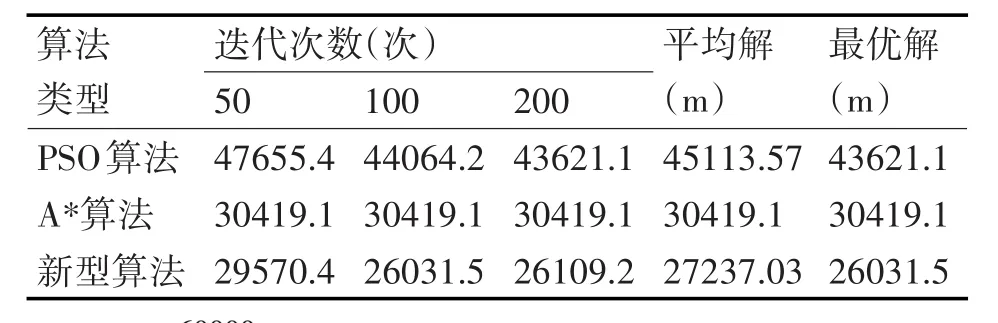
表2 三种算法结果统计

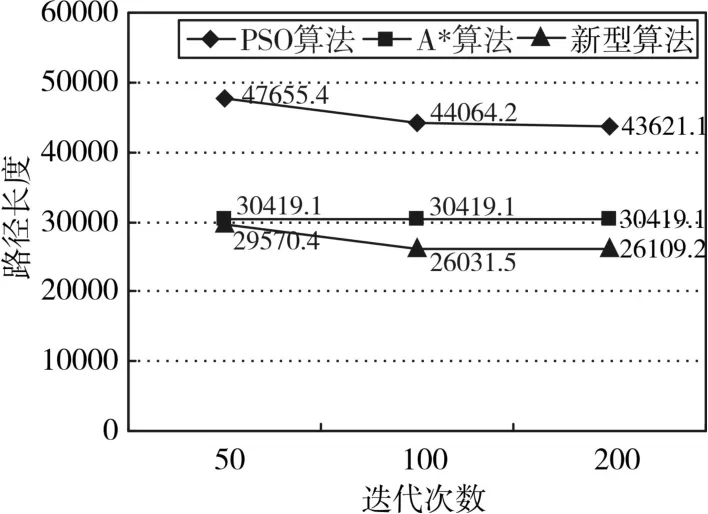
图2 路径长度对比

从表2和图2可看出不同迭代次数下，A*算法求解一致，但PSO和新型PSO算法求解的路径长度、平均解、最优解均不同。随着迭代次数的加大，算法各自求得的解都趋于最优。但是从图中明显能够看到新型PSO算法在每次不同迭代次数下的解及平均解、最优解都要优于前两个算法。这说明新型算法从解的精度看提高了原有PSO算法和A*算法的性能。新型PSO算法比原PSO算法平均减少了约17.876km，新型PSO算法比A*算法平均减少了约3.182km。

同时，从图2可看到三种算法求解结果，◆曲线代表PSO算法，■曲线代表A*算法结果，▲曲线代表新型启发式PSO算法结果。这说明新型的启发式PSO算法求解该路径问题都为最优，其具有一定实际意义和理论价值。

5 结语

本文结合市区地图数据通过数学方法利用坐标投影建立了算法环境模型，针对粒子群算法路径规划的自身不足，结合A*算法思想初始化种群、引入平滑度、调整惯性权重控制算法收敛速度和求解精度，以开销少为原则，寻找一条从起点到终点的最优路径或最短路径。实验结果表明，新型启发式PSO算法能在实际数据的二维搜索空间中再次降低寻优路径消耗，其中在粒子个数为100，迭代次数为200时解较优，较前两种算法，改进策略提高了搜索精度，而且算法过程易实现，操作过程易理解。但是，该算法的设置参数为经验值，算法性能也有待进一步研究和关注。

［1］Dillmann R，Zoellner R，Ehrenmann M.Interactive Natu⁃ral Programming of Robots：Introductory Overview［C］//Pro.of IEEE-RAS Joint Workshop on Technical Challenge for Dependable Robots in Human Environments.Tolous，France：［s.n.］，2002：253-258.

［2］Choset H，Nagatani K.Topological Simultaneous Localiza⁃tion and Mapping（SLAM）：Toward Exact Localization Without Explicit Localization［J］.IEEE Transactions on Robotics and Automation，2001，17（2）：125-137.

［3］宫金超，李晓明.基于粒子群优化算法的小型足球机器人路径规划［J］.机电工程，2010，27（12）：116-121.

GONG Jinchao，LI Xiaoming.Path planning of a small soc⁃cer robot based on particle swarm optimization algorithm［J］.Mechanical and electrical engineering，2010，27（12）：116-121.

［4］段海滨.蚁群算法原理及其应用［M］.北京：科学出版社，2005：108-119.

DUAN Haibin.Principle and application of ant colony al⁃gorithm［M］.Beijing：Science Press，2005：108-119.

［5］Kennedy J，Eberhart R.Particle swam optimization［C］//Proceedings of IEEE International Conference on Neural Network.Perth，Australia，1995：1942-1948.

［6］Eberhart R，Kennedy J.A new optimizer using particles swarm theory［C］//Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Na⁃goya，1995：39-43.

［7］张万绪，张向兰，李莹.基于改进粒子群算法的智能机器人路径规划［J］.计算机应用，2014，34（2）：510-513.

ZHANG Wanxu，ZHANG Xianglan，LI Ying.Path plan⁃ning of intelligent robots based on Improved Particle Swarm Optimization［J］.Computer applications，2014，34（2）：510-513.

［8］张铁虎，俞经虎，王琨.基于ACO-PSO算法的点胶路径规划与分析［J］.计算机应用，2016，36（S2）：89-92.

ZHANG Tiehu，YU Jinghu，WANG Kun.Dispensing path planning and analysis based on ACO-PSO algorithm［J］.Computer applications，2016，36（S2）：89-92.

［9］张成，凌有铸，陈孟元.改进蚁群算法求解移动机器人路径规划［J］.电子测量与仪器学报，2016，30（11）：1758-1764.

ZHANG Cheng，LING Youzhu，CHEN Mengyuan.Path planning of mobile robot based on an improved ant colony algorithm［J］.Journal of electronic measurement and in⁃strumentation，2016，30（11）：1758-1764.

［10］汪冲，李俊，李波，等.改进的蚁群与粒子群混合算法求解旅行商问题［J］.计算机仿真，2016，33（11）：274-279.

WANG Chong，LI Jun，LI Bo，et al.Improved ant colo⁃ny-particles swarm hybrid algorithm for solving TSP［J］.Computer simulation，2016，33（11）：274-279.

［11］毛琪波，余震虹.改进的粒子群算法在传感器温度补偿中的应用［J］.计算机工程与应用，2016，52（23）：229-235.

MAO Qibo，YU Zhenhong.Improved PSO and its applica⁃tion to sensor temperature compensation［J］.Computer Engineering and Applications，2016，52（23）：229-235.

［12］孙凯，吴红星，王浩，等.蚁群与粒子群混合算法求解TSP 问题［J］.计算机工程与应用，2012，48（34）：60-63.

SUN Kai，WU Hongxing，WANG Hao，et al.Ant colony and particle swarm optimization algorithm for TSP prob⁃lem［J］.Computer engineering and applications，2012，48（34）：60-63.

［13］朱莹莹，王宇嘉.求解复杂旅行商问题的混合粒子群算法［J］.轻工机械，2015，33（3）：42-44.

ZHU Yingying，WANG Yujia.Hybrid particle swarm op⁃timization for solving complex traveling salesman prob⁃lems［J］.Light industry，2015，33（3）：42-44.

［14］Clerc，Maurice，Discrete Paxirticle Swam Optimization［M］.New Optimization Techniques in Engineering，2004：219-240.

［15］吕方兴，方昕.一种求解最优路径的新型混合PSO算法研究［J］.计算机与现代化，2013，41（2）：165-168.

LV Fangxing，FANG Xin.A new hybrid PSO algorithm for solving optimal path［J］.Computer and modern，2013，41（2）：165-168.