皮纳卫星编队保持动力学分析
2018-03-20,,
,,
1. 北京航空航天大学 宇航学院,北京 100191 2. 北京控制工程研究所,北京 100190
近年来皮纳卫星由于其造价低廉,在编队飞行中的应用日益普遍,国际上对分布式小卫星系统技术要求水平不断提高。编队卫星当前轨道控制精度一般为毫米级,姿态控制精度一般为0.5°,而国内多颗小卫星在轨运行中都出现了飞轮系统过早失灵的情况。
2015年起,欧洲对卫星编队的轨道控制精度要求达到了毫米以下,美国更是将编队飞行控制精度提高到了微米甚至纳米级[1],早在2002年就于GRACE两星串联编队上提出了距离与速率测量精度分别要达到1 μm和1 μm/s的要求,空间激光干涉引力波探测项目(Laser Interferometer Space Antenna,LISA)中3个航天器相互位置关系精度要求在米级以下,因此精度要求高于10-9[2],超高精度的位置要求必需由超高精度的控制系统来完成。
场发射电推力器(Field Emission Electric Propulsion,FEEP)单个发射器推力为0.5~100 μN,通过设计安装瞬间开关功能[3],可以用于微牛顿量级的扰动补偿系统;美国喷气推进实验室(Jet Propulsion Laboratory,JPL)研制的微型氙离子推力器,质量仅有0.2 kg[4],单台寿命长达15 000 h以上。欧洲航天局(European Space Agency,ESA)和美国国家航空航天局(National Aeronautic and Space Administration,NASA)为满足LISA先驱者任务的推力和载荷要求,研制出包含9个铟液态金属离子源(Liquid Metal Ion Source,LMIS)的FEEP簇,每个LMIS携带铟15 g,最大推力100 μN,在结构上集成前置电阻,使FEEP簇共用一个电源,这样既满足了推力分辨率,又增加了最大推力,整体质量大大减少。
皮纳卫星编队轨道控制精度的提高对于控制方法也有更高的要求。一般用C-W方程研究近距离卫星编队构型的控制[5-7],典型的控制方法有LQR方法、Lyapunov方法[7]、滑模方法[8-10];文献[8]采用了线性最小滑模误差反馈法,用于抵抗飞行过程中遇到的大扰动;文献[11]采用了基于视线角观察值的编队构型保持方法;文献[12]考虑了外部干扰下连续时间导航和制导混合的控制方法。上述控制方法的控制精度普遍在米级或者毫米级,不能满足消除微小扰动、节省能量及延长在轨时间[13-14]的要求。而bang-bang控制方法对模型参数变化及各种干扰的响应能力都较强,可以对小推力器的推力小、系统响应慢,以及收敛时间长等不足进行弥补。
本文针对目前皮纳卫星在编队飞行中只有毫米级控制精度,难以满足对地定向等应用需求,提出了在小推力作用下的bang-bang高精度的编队控制律,很好地解决了皮纳卫星编队构型保持问题,为皮纳卫星编队构型的设计提供理论指导。仿真表明,提出的控制方法不但可以使系统快速收敛,同时还能使皮纳卫星编队的星间控制精度达到1 μm,与滑模控制律相比较,精度提高近103倍。
1 编队构型控制模型
1.1 编队卫星动力学方程
则,第i颗卫星的动力学方程组表示为:
(1)
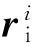

(2)
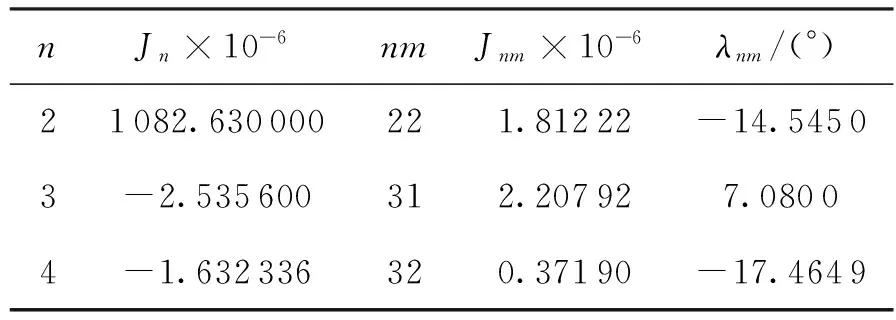
式中:扁率摄动系数取J2、J3、J4三项,见表1;fD=(fDx,fDy,fDz);CD为阻力系数,自由分子流中取常数CD=2.2;S/m为卫星的面质比;ρ为卫星所在空间的大气密度;V=v-va为卫星相对于大气的运动速度;m′为第三体质量,其他各量意义如图1所示;p为太阳辐射压强,取为常数p=4.65×10-6N/m2;RS为太阳方向,RS=(cosΛ,sinΛcosε,sinΛsinε),其中,Λ为太阳在黄道上的黄经;ε为黄赤交角,约为23°26′,太阳黄经由历法计算;k为材料吸光系数,取值如下:

表1 地球扁率摄动系数
nJn×10-6nmJnm×10-6λnm/(°)21082.630000221.81222-14.54503-2.535600312.207927.08004-1.632336320.37190-17.4649

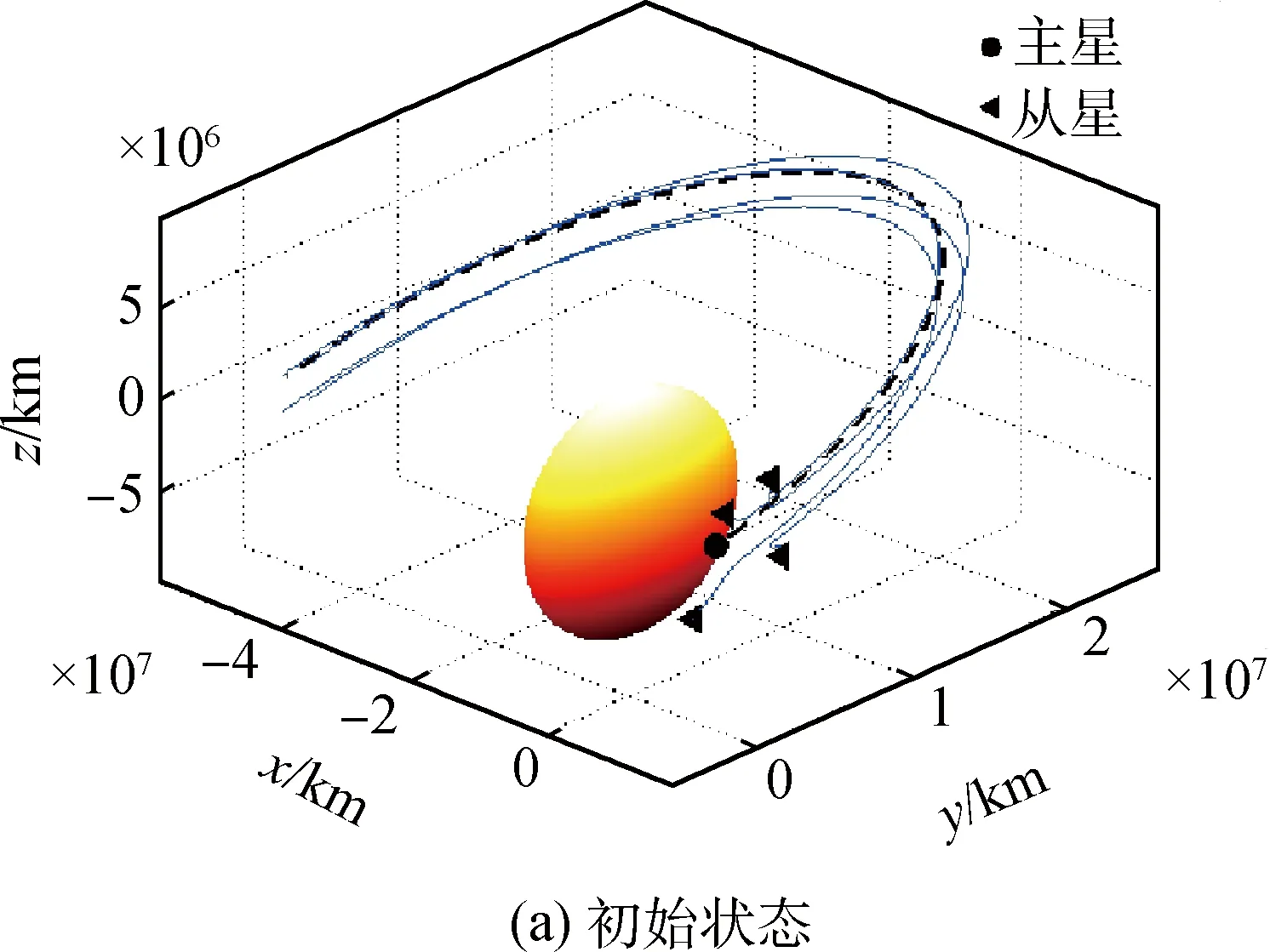
图1 三体力学模型简图Fig.1 Model of three-body problem
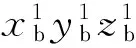
(3)
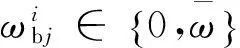
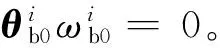

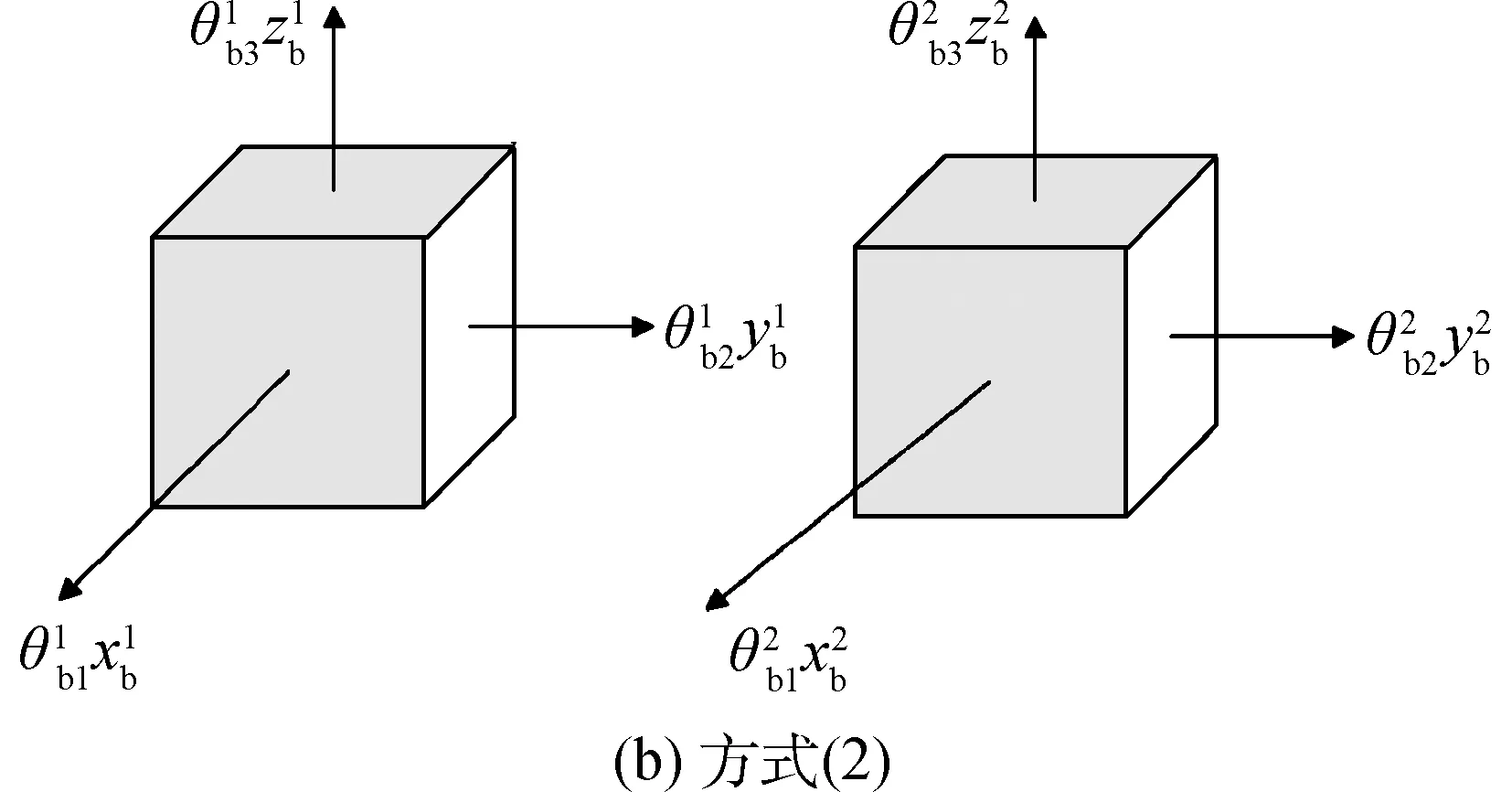
图2 推力器分布示意Fig.2 Diagram of the thruster distribution
定义两卫星间的编队构型参数为:
编队构型参数的几何意义如图3所示。

图3 编队构型参数(dF,αF,βF)几何示意Fig.3 Geometric diagram of the formation parameters (dF,αF,βF)
图3中dF为星间距离,αF为从星与主星的连线相对于xioiyi平面的夹角,βF为从星与主星的连线在xioiyi平面投影相对于oixi轴的夹角。
1.2 三轴解耦相对状态方程
定义相对状态矢量为:
(5)
式中:
则,卫星编队的相对动力学方程为:
(6)

编队构型参数稳定可等价于保持相对状态矢量稳定在理想的相对状态矢量:

(7)
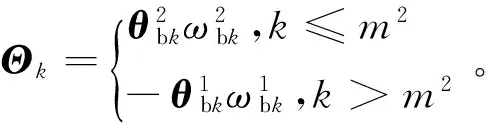
改写式(6)为:
(8)
式中:σk∈{-1,0,1}为分片常值函数,k=1,2,3。
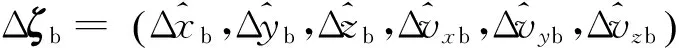
(9)
将式(9)代入式(8),得到相对动力学误差模型:
(10)
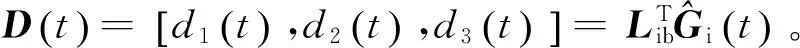
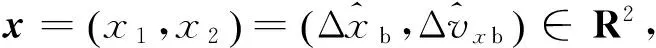
(11)
式中:控制输入σ∈{-1,0,1},其他子系统类同。
1)对所有r>0都存在控制参数使得x0∈R2,且对所有t0∈R都存在T>0使得对所有t≥T都满足φ(t,t0,x0)∈Br(0);
2)在任意给定的较小时间间隔[t0,t1]内,控制输入σ都在有限次数内完成。即必须在一个闭区间的时间间隔内通过有限次数的开关完成编队构型保持。
2 基于bang-bang控制的连续-离散混合控制器
bang-bang控制将状态空间(即相平面)分为两个区域,分别对应于控制变量取正的最大值和取负的最小值,保证使轨迹趋向原点的切换频率是有限的,由此可以提高推力器的分辨率,实现高精度控制。而bang-bang控制最短时间控制器的开关面设计,可以改善小推力对卫星编队快速机动的敏感不足。采用连续和离散状态混合的控制律设计,能够通过离散控制律的状态减少推力器的开关切换次数,延长推力器工作寿命。
2.1 开关面设计
基于最短时间控制器得到切换面如下:
Γ+和Γ-分别为如图4所示的两块区域,开关面表示为:
两条开关线的表达式为:
(12)
为了消除滑模影响,增加开关线x2=0,组成区域Σ+和Σ-,该区域保证使轨迹趋向原点的切换频率是有限的。
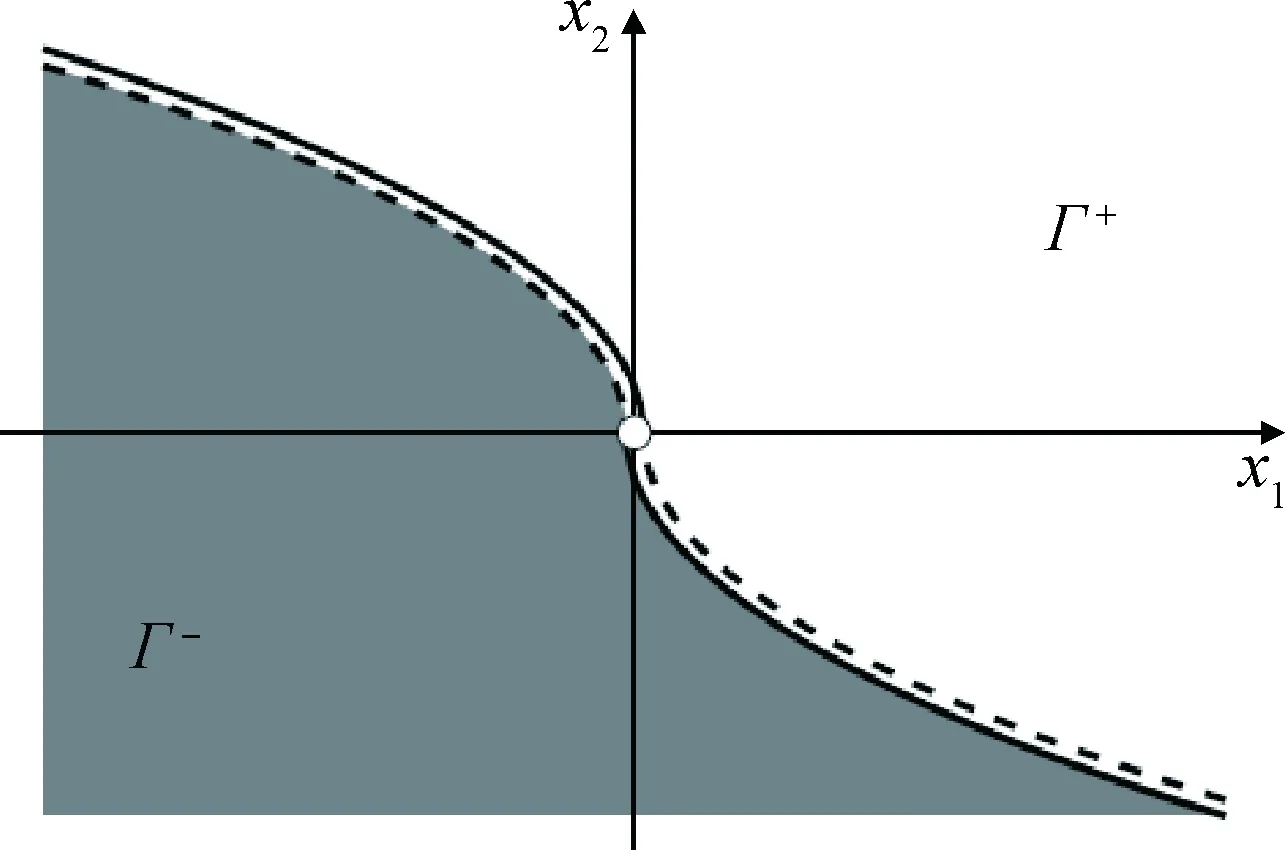
图4 Γ+和Γ-的几何意义Fig.4 Geometric diagram ofΓ+and Γ-
Σ+和Σ-如图5所示,表达式为:

(13)

图5 切换平面Σ+和Σ-Fig.5 Geometric diagram ofΣ+and Σ-
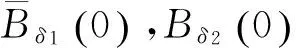
(14)
2.2 控制律
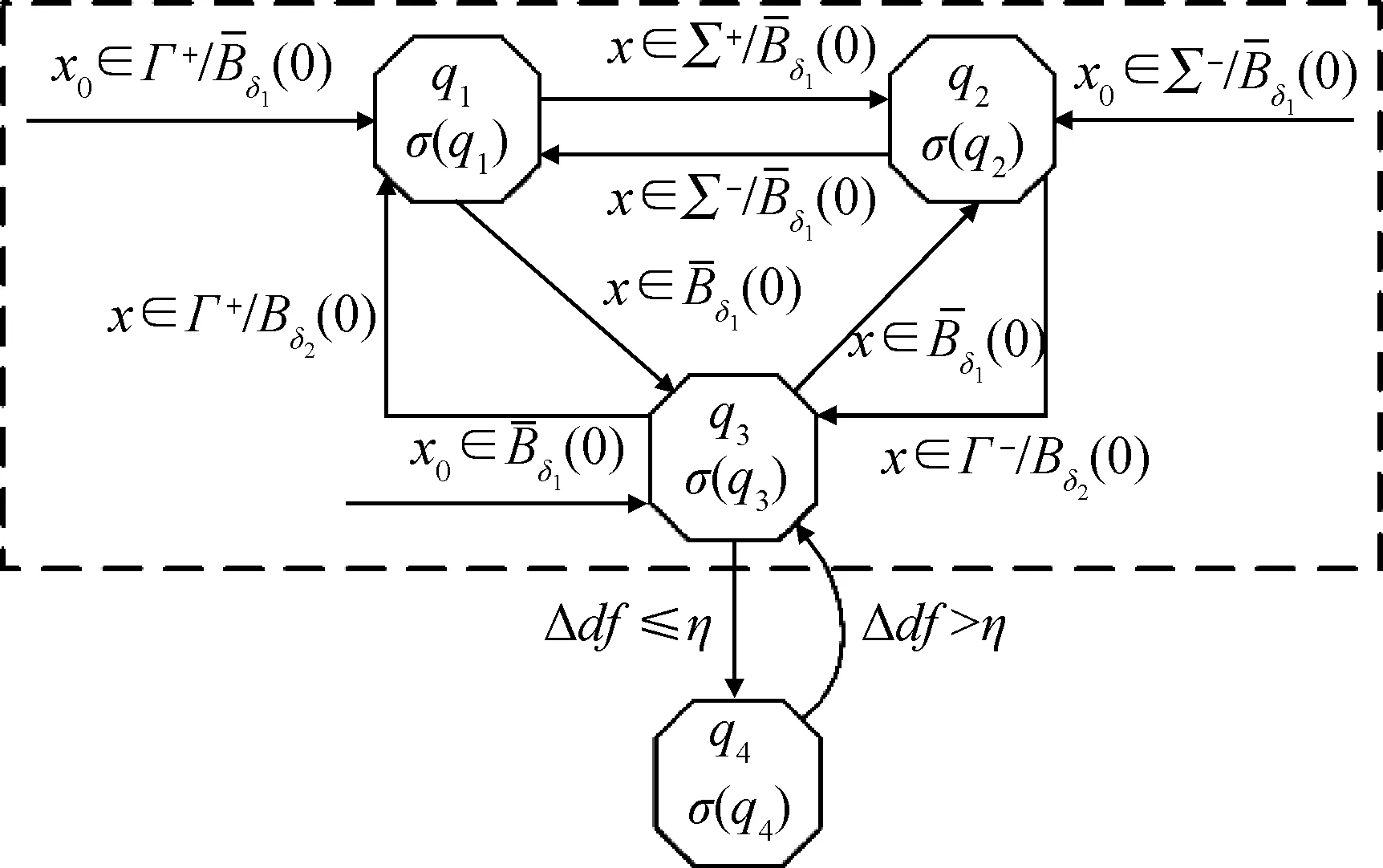
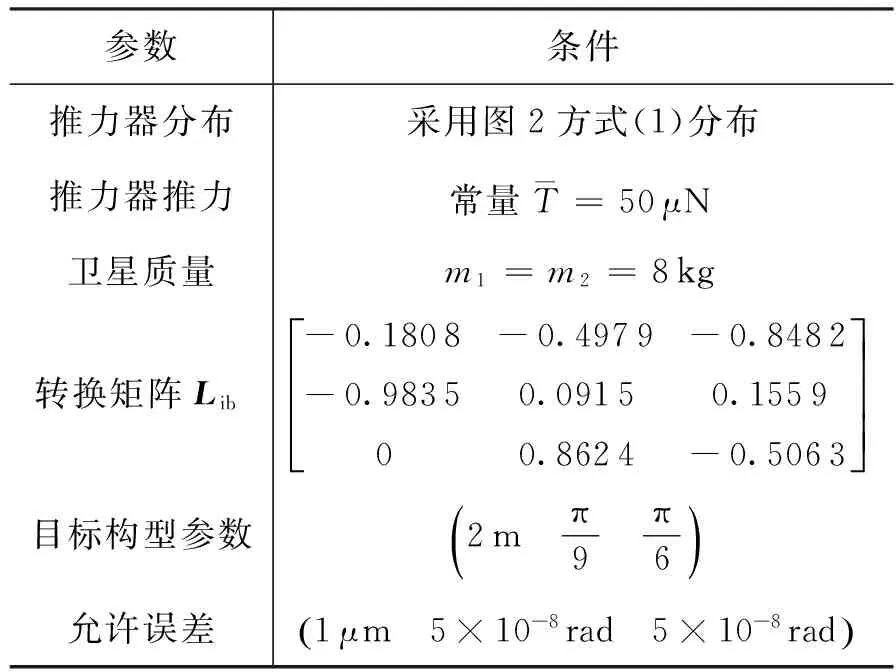
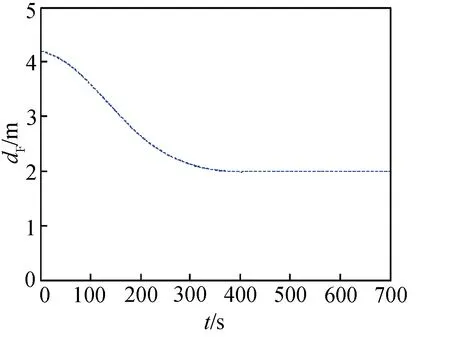
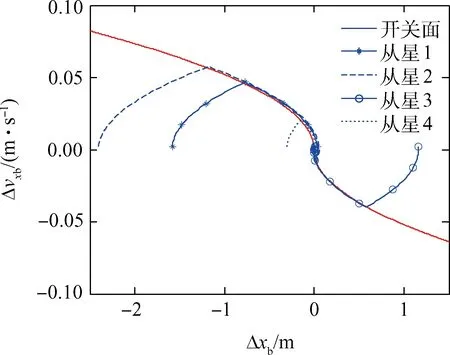
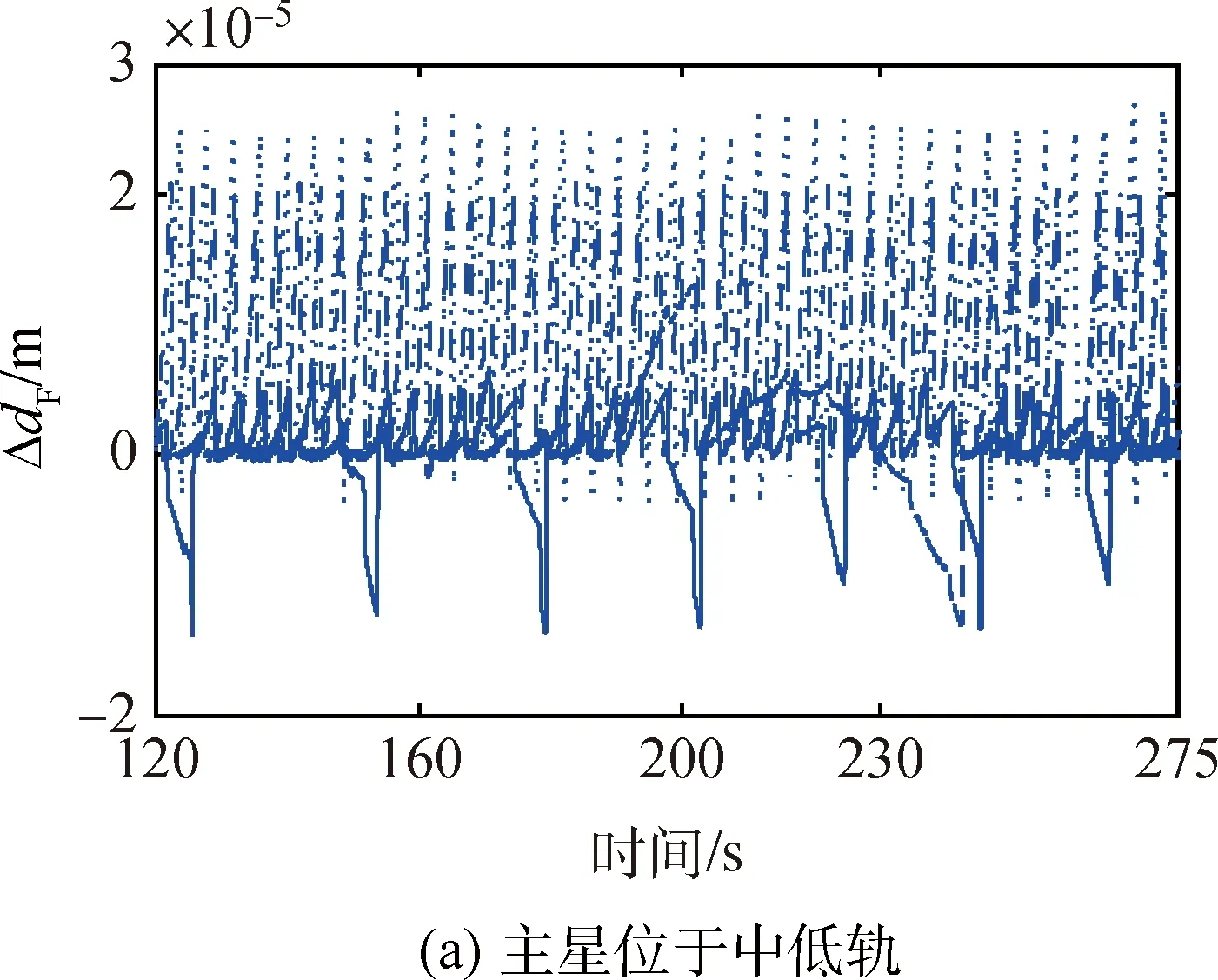
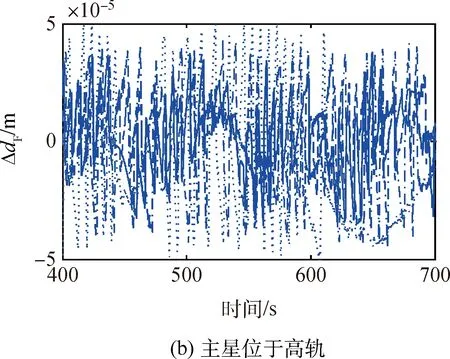
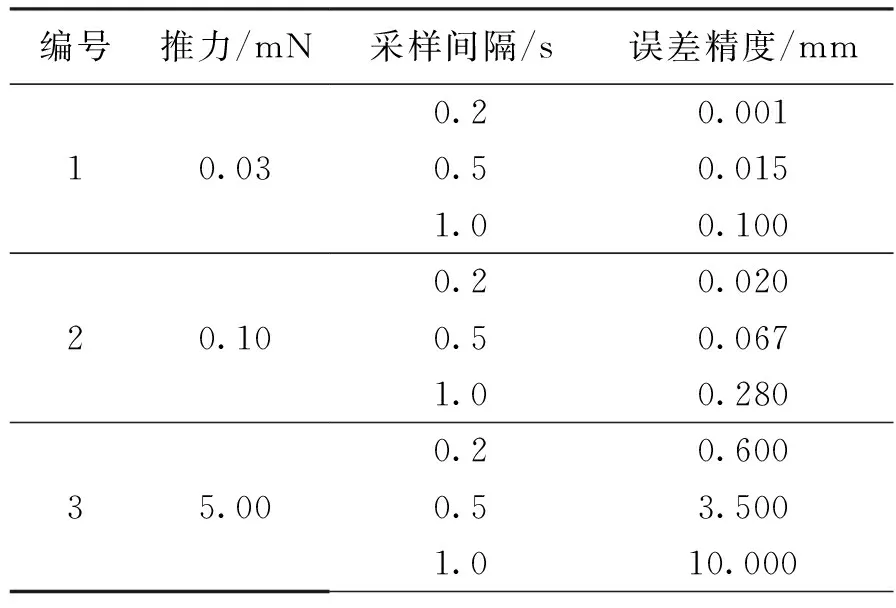
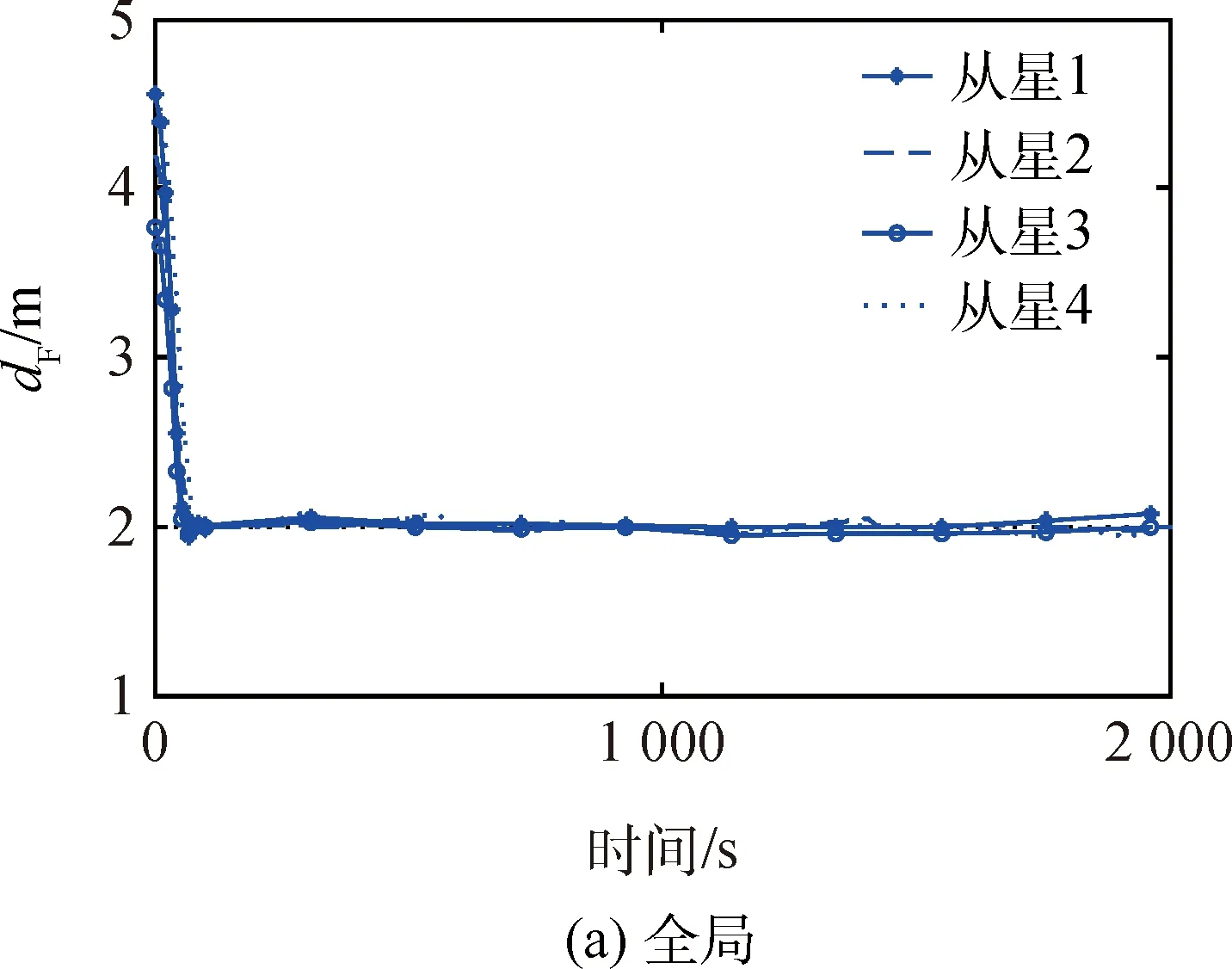
令0<δ1<δ2 (1)精度优化控制律 提出一种混合控制律,运用离散状态qi激活和反激活切换曲线Σ+和Σ-。 精度优化控制律由图6有限状态机中虚线方框内的过程给出,图中Q={q1,q2,q3}为离散状态,x∈R2为连续状态,σ(·):Q→R为混合反馈,精度优化控制律表示为: (15) 参数选择条件如下: 2)δ2的取值必须远小于r,其值可以按如下条件选取: 当: (16) 否则, (17) 3)δ1是满足小于δ2的正数,且δ1的取值会影响控制器式(15)的切换频率,δ1越大会导致开关次数越多。 图6 表示控制律的有限状态机Fig.6 Finite-state machine of the control theory (2)能量优化控制律 假设稳定阶段只受摄动影响的小扰动,为节省燃料,减少推力器工作时间,延长在轨工作寿命,在控制律式(15)的基础上添加最大容许误差限η,当控制误差Δdf小于η时,不施加控制;反之再施加控制,控制律实现过程由图6整体描述,具体表示为: (18) 其他相关参数的选择同精度优化控制律。 仿真条件如表2所示。 表2 仿真条件 根据精度优化控制律式(15)进行仿真分析。 3.1.1 稳定领域r变化的仿真讨论 初始条件如表3所示。 表3 初始条件 图7给出了星间距离dF随时间的变化曲线,可看出最终星间距离稳定在事先给定的2 m。 图8分别给出了r取不同值时,稳定阶段的星间距离误差ΔdF随时间的变化曲线和卫星某个正向推力器的开关状态曲线。比较得出: 图7 星间距离dF随时间变化曲线Fig.7 Curve of the dF changing with the time 1)误差dF保持在高精度范围内; 2)当r=0.001 8时,改变推力器开关状态并不频繁,且构型保持阶段推力器开启时间只持续数秒; 3)稳定区域半径r取值越小,则星间距离误差越小,但相应的推力器开关次数变的越频繁。 图8 r对稳定阶段的星间距离误差ΔdF和推力器开关状态的影响Fig.8 Curves of the ΔdF and the x-axis thruster′s states with different r 3.1.2 高中低轨飞行的控制精度分析 初始条件如表4所示。研究主星分别位于高、中、低轨时的飞行情况,并与滑模控制方法进行比较。 从图9可以看出,4颗从星的编队构型的相轨迹能很快地收敛至原点,符合要求。 由图10可以看出,在考虑摄动因素情况下,主星位于高、中、低轨时星间距离精度均能保持在30~50 μm范围内,而对比文献[16]中采用的基于终端滑模控制器,最终达到0.002 455 m的精度,明显本文方法更有优势。 表4 初始条件 由图11可以看出,当4颗从星受到较大扰动偏离标准轨道时,采用本文控制方法后,卫星很快回到目标轨道,并且构型保持在稳定范围内。 3.1.3 参数改变的影响分析 (1)不同轨道高度 在卫星质量8 kg条件下,改变参数δ1和δ2,仿真结果如表5所示。 图9 Δvxb-Δxb分系统相平面构型曲线Fig.9 Phase plane curve of theΔvxb-Δxb subsystem 图10 各个从星距离误差ΔdF随时间变化曲线Fig.10 Curve of the ΔdF changing with the time 由表5可知: 1)本文控制律对各种高度轨道飞行器均有良好的控制特性; 2)随着轨道高度减小,摄动力增大,所需推力也相应增大,若需达到高轨同样的精度,推力器的切换频率将大大增加; 3)调整δ1和δ2可以减小误差,但相应推力器的切换频率将会变大,且不施加控制的时间缩短,因此,需要兼顾切换频率、控制时间及误差。 (2)不同推力分辨率 当放宽对推力器推力分辨率及开关时间的要求,得到表6的结果。 表6说明推力器的推力越小,采样时间越短,则误差越小,在推力为0.03 mN时,轨道控制精度最小可以达到1 μm,目前小推力器最小推力已经能够达到微牛量级,所以星间距离精度有望达到纳米级。 表5 仿真结果1 注:轨道高度n1为地球半径(6 378 km)的倍数。 表6 仿真结果2 基于能量优化控制律式(18),以表5中的高轨为例,当星间距离稳定在精度范围内10 s后一定时间内不施加控制,当位置误差大于要求精度时,再重新施加控制,得到仿真结果见表7。 由表7可知: 1)不施加控制的时间与推力大小无关,只与星间距离最大允许误差有关; 2)当推力器的分辨率达到0.1 N时,星间距离的均方根误差依然能达到0.2 mm左右,且星间距离误差几秒内快速收敛; 3)星间距离的误差范围增大,可以使不施加控制的时间增长,但同时卫星回到规定精度所需的时间和能量均需要增加;因此,需要权衡利弊使系统获得性能最优。 以表6中第1组第1种情况即推力0.03 mN,采样间隔0.2 s为例进行仿真,结果如图12所示。 表7 仿真结果3 图12 各个从星星间距离dF随时间变化曲线Fig.12 Curve of the dF changing with the time 由图12可以看出,当星间距离误差收敛到要求精度30 μm内10 s后,不再对卫星施加控制;在不控制区间,要求星间距离误差不超过0.1 m,一旦超过0.1 m,控制系统重新启动,星间距离误差快速收敛,回到30 μm内,循环往复。可以看出,一定时间不施加控制的方法,可以延长在轨寿命。 针对基于小推力高精度的皮纳卫星编队构型控制开展研究,结果如下: 1)根据小推力变化缓慢的控制特性,建立三轴解耦的相对状态方程,分别对各子系统进行控制律设计; 2)采用时间最优条件设计bang-bang控制器开关面,提高小推力推力器控制的快速响应特性; 3)通过有限状态机设计精度优化控制律,使其对轨道参数及摄动大小等的变化更具有鲁棒性; 4)设置误差门限控制推力器工作时间,设计能量优化控制律,由此不但节省燃料,而且延长卫星的在轨寿命; 5)本文提出的基于bang-bang控制的连续-离散混合控制方法使皮纳卫星编队星间保持精度提高到1 μm,相比于滑模控制方法的保持精度提高103倍。 References) [1] 林来兴.分布式小卫星系统的技术发展与应用前景[J].航天器工程,2010,19(1):60-66. LIN L X. Technological development and application prospects of distributed small satellite system[J].Spacecraft Engineering,2010,19(1):60-66(in Chinese). [2] 段君毅.场致发射电推力器工作性能及其发射机理研究[D].上海:上海交通大学,2011:9-17. DUAN J Y. Research on operation characteristics and emission mechanism of field emission electric propulsion[D]. Shanghai:Shanghai Jiao Tong University,2011:9-17(in Chinese). [3] SALVO M,ANGELO G,MARIANO A. Experimental performance of field emission micro-thrusters[J].Journal of Propulsion and Power,1998,14(5):774-781. [4] 林来兴.现代小卫星的微推进系统[J].航天器工程,2010,19(6):13-20. LIN L X. Micro-propulsion system for modern small satellites[J].Spacecraft Engineering,2010,19(6):13-20(in Chinese). [5] DUAN X D,BAINUM M P. Low-thrust autonomous control for maintaining formation and constellation orbits[C]∥AIAA/AAS Astrodynamics Specialist Conference and Exhibit,Providence.Rhode Island:AIAA Press,2004,53(1):65-82. [6] 张杨,侯明善,刘永刚.卫星编队长期保持与控制比较研究[J].计算机仿真,2009,26(11):41-45. ZHANG Y,HOU M S,LIU Y G. A comparison of long-term keeping and control for satellite formation flying[J].Computer Simulation,2009,26(11):41-45(in Chinese). [7] 范林东,杨博,苗峻,等. 基于SiCMEMS阵列的高精度微纳卫星编队保持[J]. 中国空间科学技术,2016,36(2):37-45. FAN L D,YANG B,MIAO J,et al.High precision micro-nano satellite formation keeping based on SiC MEMS micro thruster array[J].Chinese Space Science and Technology,2016,36(2):37-45(in Chinese). [8] CAO L,CHEN X. Input-output linearization minimum sliding-mode error feedback control for spacecraft formation with large perturbations[J].Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering,2014,229(2):352-368. [9] 李程.椭圆轨道卫星编队保持控制算法研究[D].哈尔滨:哈尔滨工业大学,2014:21-34. LI C. Algorithm on satellite formation keeping along eccentric orbit[D].Harbin:Harbin Institute of Technology,2014:21-34(in Chinese). [10] 郭耀华. 基于一致性理论的卫星编队滑模/反步协同控制研究[D].北京:北京理工大学,2015:66-73. GUO Y H. Sliding mode/backstepping coordinated control of satellite formation based on consensus theory[D].Beijing:Beijing Institute of Technology,2015:66-73(in Chinese). [11] WU T H,LEE T. Spacecraft position and attitude formation control using line-of-sight observations[C]∥Decision and Control (CDC)2014 IEEE 53rdAnnual Conference on,Los Angeles,CA,USA:IEEE,2014:970-975. [12] LEE D,VISWANATHAN S P,HOLGUIN L,et al. Decentralized guidance and control for spacecraft formation flying using virtual leader configuration[J].Proceedings of the American Control Conference,2013,343(6174):4826-4831. [13] 张天平,周昊澄,孙小菁,等.小卫星领域应用电推进技术的评述[J].真空与低温,2014,20(4):187-192. ZHANG T P,ZHOU H C,SUN X J,et al .Review of electric propulsion applicable to small satellites[J].Vacuum and Cryogenics,2014,20(4):187-192(in Chinese). [14] 田立成,王小永,张天平.空间电推进应用及技术发展趋势[J].火箭与推进,2015,41(3):7-14. TIAN L C,WANG X Y,ZHANG T P,et al. Application and development trend of space electric propulsion technology[J].Journal of Rocket Propulsion,2015,41(3):7-14(in Chinese). [15] RAO V G,BERNSTEIN D S. Naive control of the double integrator[J].IEEE Control Systems,2001,21(5):86-97. [16] 黄勇,李小将,王志恒,等.基于终端滑模的卫星编队飞行有限时间控制[J].空间科学学报,2014,34(1):109-115. HAUNG Y,LI X J,WANG Z H,et al. Finite-time control of satellite formation based on terminal sliding mode[J].Chinese Journal of Space Science,2014,34(1):109-115(in Chinese).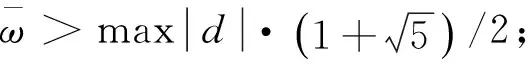


3 数值仿真
3.1 精度优化控制律仿真






3.2 能量优化控制律仿真分析


4 结束语
