空间3自由度并联机构运动螺旋运动分析

王丽，王益轩

（1.西安工程大学，陕西 西安 710048；2.陕西工业职业技术学院，陕西 咸阳 712000）

引言

由并联机构发展起来的各种并联机器普遍具有刚度精度高、承载能力强而运动负荷小的优点，但是并联机构复杂的结构特征使得它的许多机构学问题变得极其困难，为此诸多的数学方法被引用到机构的理论研究中。尽管各种方法所表示的机构学特征实质是相同的，但却有不同的特点。螺旋理论在机构的许多问题的研究中都有应用， Yang[1]提出一种利用有限螺旋合成3自由度并联机构的方法，得到机构的空间拓扑结构。陈子明[2]通过分析机构螺旋系线性相关的条件得出奇异位形的判别方程。柴馨雪[3]利用螺旋理论建立机构运动学反解方程，得到机构约束奇异和运动学奇异的判别条件。Jaime[4]利螺旋理论分析了3-CRS并联机构的运动学，得到机构的输入输出速度、加速度关系方程。Guan[5]用螺旋表示每个关节的运动，利用反螺旋的性质得到每个分支施加给动平台的约束螺旋，分析了机构发生奇异的三种条件。熊有伦[6]以矢量积和微分运动分析的方法建立机器人机构的速度雅克比矩阵，黄真[7,8]以机构的影响系数建立并联机构构件之间的速度关系矩阵。本文将相邻构件的相对运动表示成运动螺旋，以它们的线性组合构造运动链末端构件的运动螺旋，导出机构正向和逆向速度关系方程。

1 机构的结构约束

空间3自由度并联机构动平台通过三条相同的运动链与基座相连，每条支链具有一个转动副、一个移动副和一个球面副，如图1所示。

图1 空间3自由度并联机构运动简图

选取参考坐标系 O-xyz 和动坐标系 C-x′y′z′，Br在坐标系O-xyz的位置矢量

B′r——Br在坐标系 C-x′y′z′的位置矢量

R——坐标系 C-x′y′z′对 O-xyz 旋转变换矩阵

α、β、γ——动坐标系 C-x′y′z′绕 x、y、z轴的转角

受移动副和转动副的结构限制，Br始终位于与坐标面平行的平面上，有一个坐标保持不变。

式中a,b——分别为OAr和BrC的长度。由式(2)可得，

上式表明，动平台的位置参数和姿态参数并非彼此独立，将上式对时间t求导，可得到动平台平动速度和转动角速度之间的关系，即机构运动约束。

2 构件的瞬时运动螺旋

为了分析动平台的瞬时运动，将机构的球面副用三个轴线垂直相交的转动副表示，如图2所示。每个分支有5个活动构件，用0,1,…,5标记，在分支r中，中间连杆i (i=1,2,3,4)都有两个关节，与它固连的坐标系记为，轴取在前一个关节轴线方向，轴取在连杆两关节轴线的公法线方向。与机架固连的坐标系记为，取成和重合，取成关节1转角度量的起点方向。与构件5（即动平台）固连的坐标系，轴取在关节轴线上，轴取成当该关节转角等于零时与轴重合。在选取坐标系后，可以从中定义连杆运动学参数（D–H参数），如表1所示。

图2 空间3-RPS并联机构等效运动简图

表1 连杆运动学参数（D–H参数）

在分支中，如果构件i与i-1通过转动关节相连，它们之间的相对运动是绕关节轴线的转动，轴线的空间位置可以用一个单位螺旋表示：

如果构件i与i-1通过移动关节相连，它对构件i-1的相对运动是沿着关节轴线方向的平动，移动关节的运动螺旋。

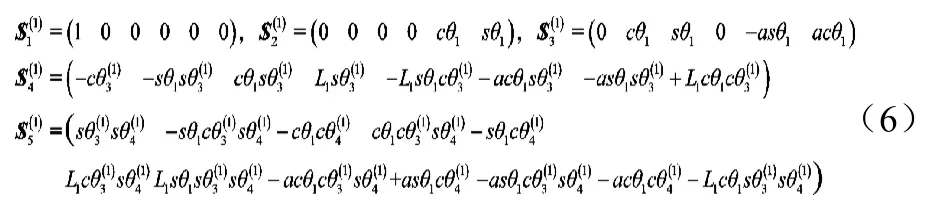
3 动平台的螺旋运动描述

在机构路径规划中，一般是按作业性质给出动平台角速度矢量ωS和动平台上最具特征的称参考点P的线速度vp,将动平台的运动用螺旋表示：

其中，角速度矢量ωS与坐标原点的选取无关，ωS0代表动平台上与坐标原点重合的那一点的速度。螺旋的节距是原点不变量，如果将原点选在动平台的P点，则动平台的运动螺旋为：

这样便能求出动平台运动螺旋的节距：

图3 运动螺旋分解

将速度vp沿着角速度矢量及其垂直方向进行正交分解，如图3所示，在角速度矢量方向的分量为，另一分量为，所以式(8)可以写成以下两个螺旋之和第一个螺旋中是一个线矢量，由它可以确定出螺旋ωS/转动轴线在坐标系{P}的位置方程：

4 并联机构正向运动学

并联机构的正向运动学即是由主动关节速度求得动平台速度，动平台通过分支上的运动链连接到基座，它的运动螺旋应该是分支所有运动螺旋的线性组合。

对于任意两个分支：

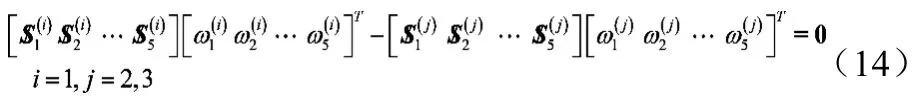
上式是以全部从动关节速度为未知数的线性代数方程组，可以从中解得所有关节速度，动平台的瞬时运动螺旋可以由式(13)从任意一个分支中得到。

5 并联机构逆向运动学

设刚体的瞬时运动螺旋和为受到的力螺旋分别为：

刚体以角速度ω1绕轴线S1转动又以速度h1ω1沿轴线移动，同时又受到沿S2方向的作用力f2S2和力偶矩h2f2S2，两螺旋的互易积，即一个螺旋的原部矢量与另一个螺旋的对偶部矢量的数量积之和，它代表了刚体的瞬时功率。如果两螺旋互易积等于零，则它们互为反螺旋，如果螺旋用坐标表示，互逆性条件可以表示成：

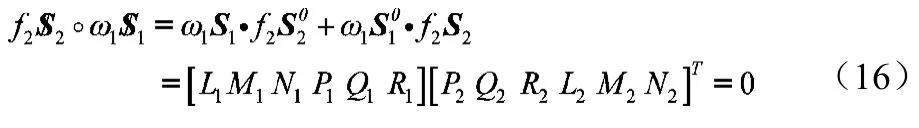
机构的逆向运动学即是由动平台速度求得所有关节速度，式(13)包含了每个分支未知的关节速度变量，而给出的等式却有6个，在求解时必须考虑动平台受到的约束。现在从每个分支后面关节开始向前递推，并仅以第一个分支为例说明求解过程，其余分支的求解也类似。机构每个分支5个关节运动螺旋构成Ⅴ系螺旋，因而有唯一的反螺旋，记作，由反螺旋的性质式(16)，得：

系数矩阵右下角的R2×2分块矩阵的行列式等于零，所以方程解向量的最后两个分量必须为零，剩下的前3个方程含有4个未知数，需要指定其中的一个，解得反螺旋。

反螺旋的表示式中有一个独立的未知参数x4可以任意取值，但不能取为0。为了求第5个关节速度，取前四个关节的运动螺旋，它们构成了一个Ⅳ系螺旋，有两个线性无关的反螺旋，满足为其中的一个，从中解得反螺旋系：

它有两个独立的参数x6和x4，可以任意取值，对比和选取其中与线性无关的哪一个对式(13)的两边作互易积：

相逆的两螺旋互易积等于零，上式右边第一项等于零，从而求得：

它有3个独立的未知参数x6、x4和x3，可以任意取值，选取其中与和线性无关而的哪一个对式(13)的两边作互易积：

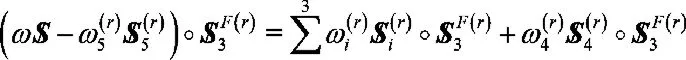
相逆的两螺旋互易积等于零，上式右边第一项等于零，从而求得：

它有4个独立的未知参数x6、x4、x3和x2，可任意取值，选取其中与和线性无关的哪一个对式(13)的两边作互易积：

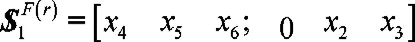
6 应用实例

给定机构结构参数和动平台的运动规律：a=980mm，b=600mm。

按式(22)和(21)可求得机构所有主动关节和移动关节速度，如图 4所示。主动关节转动角速度的变化范围为–0.2～0.2rad.s-1，移动关节速度的变化范围为–0.3～0.3 m.s-1，将它们分别与动平台的平动速度和转动角速度比较，它们的比值在一定程度代表了机构瞬时功率的传递关系。

7 结论

（1）将机构的关节相对运动表示成运动螺旋，得到并联机构的正向运动学方程，动平台及所有从动关节的运动速度都可以由主动关节速度线性地表示出来。

（2）螺旋理论对机构每个分支采用从后向前递推的方法，确定不同阶螺旋系的反螺旋，得到所有关节速度与动平台速度的关系方程。

[1] Shuo fei Yang, Tao Sun ,Tian Huang, etal. A finite screw approach to type synthesis of three-DOF translational parallel mechanisms [J].Mechanism and Machine Theory,2016, 104:405-419.

[2] 陈子明,黄坤, 刘晓檬.空间单环R/PSC机构的运动和奇异分析[J].机械工程学报,2016,52 (13): 17-24.

[3] 柴馨雪,项济南,李秦川.2-UPR-RPU 并联机构奇异分析[J].机械工程学报,2015,51(13):144-151.

[4] Gallardo-Alvarado Jaime. Kinematics of a Class of Three-Legged Parallel Manipulators by Means of Screw Theory [J]. Ingenieria Investigacion Y Tecnologia, 2016, 17(2):191-200.

[5] Li-Wen Guan, Jin-Song Wang, Li-Ping Wang. Mobility Analysis of the 3-UPU Parallel Mechanism Based on Screw Theory[C]. Procee-dings of the 2004 International Conference on Intelligent Mechatro-nics and Automation Chengdu, China, 2004, 309-314.

[6] 熊有伦,丁汉,刘恩仓编著.机器人学[M].机械工业出版社1993.

[7] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社, 2006.

[8] 黄真,孔令富,方跃法著.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.