汽车碰撞吸能铝合金力学性能试验及仿真研究

乔曦，欧阳俊，龙瑶

（广州汽车集团股份有限公司汽车工程研究院碰撞与安全部，广东 广州 511434）

前言

铝合金在航空、航天、汽车、船舶及化学工业中已大量应用。汽车用的铝合金主要有 2000系列(Al-Cu-Mg)、5000系列(Al-Mg)和6000系列(Al-Mg-Si)等。其中，5000系列铝合金，镁为主要合金元素，是热处理不可强化合金，主要特点为比强度高、密度低、延伸率高等，因而具有良好的吸能性能，常被用于车辆碰撞吸能等结构中，如吸能梁等。车辆中的碰撞吸能结构在碰撞事故中，往往为高应变率下的大变形行为，因此在这些结构的设计中需要充分考虑到吸能材料本身的大应变阶段及高应变率下的力学行为。铝合金属于典型的弹塑性材料，且其力学性能易受应变率影响[1-2]。因而，将铝合金材料用于车辆碰撞吸能结构中时，需要掌握其高应变率下塑性阶段的力学性能，从而有利于研究人员设计出更为合理的铝合金车辆碰撞吸能结构。

在现今的汽车设计中，仿真模拟成为重要的设计手段之一，如何在仿真模拟中利用准确的材料本构模型来描述材料的力学行为对于仿真精度有着至关重要的影响。目前，常用的仿真软件中，可考虑应变率效应，且用于描述金属材料的弹塑性本构模型有Johnson-Cook (J-C)模型、Cowper-Symonds(C-S)模型和Plastic-Kinematic (P-K)模型等。国内对铝合金材料的模拟多以J-C材料模型为主，如李春雷[3]等对2A12铝合金本构关系进行了试验研究，分析了应变率强化效应和温度软化效应，并得出了该材料的 J-C模型参数。林木森[4]等对三种不同加工及热处理状态的 5A06铝合金在不同温度及应变率下的力学行为进行了研究，并对根据试验数据拟合得到的J-C本构模型中的应变率强化项进行了修正。

上述的研究中，均仅限于J-C模型方面的参数获取，未考虑另外两种本构模型的情况。本文开展了5357铝合金常温下在准静态及应变率分别为0.001s-1、0.1 s-1和200 s-1下的单轴拉伸试验，在此基础上，利用试验数据拟合得到了该铝合金材料的三种本构模型的参数。其后，利用LS-DYNA (LSTC,Livermore, CA, USA)软件中的MAT_3号（P-K材料模型），MAT_15号 (J-C材料模型)以及 MAT_24号(C-P材料模型)开展仿真分析，对比研究了上述三种本构模型对该铝合金的模拟情况。

1 5357铝合金力学性能试验

1.1 低应变率试验及结果

本文中5357铝合金的主要化学成分见表1：

表1 5357铝合金的化学成分(质量分数%)

采用Instron材料试验机进行准静态及应变率0.001s-1、0.1s-1的材料拉伸试验。试件尺寸的加工及试验方法均按照GB228-2002中的有关规定进行，试件形状尺寸如图 1(a)所示，试验后的试件情况如1(b)所示。

常温下 5357铝合金试件在三种拉伸速度下的真实应力应变曲线如图2所示，图中曲线表明，准静态拉伸时铝合金的屈服应力为331Mpa，应变率为0.001s-1和0.1s-1时屈服应力分别为337Mpa和363Mpa，相比准静态屈服应力分别增加了 1.8%和 9.7%。同时从图中还可以看到，材料在三种拉伸速度下均没有出现明显的屈服平台，进入塑性阶段后应变强化并不明显，且不同应变率下的应力应变曲线之间呈现大致平行的趋势，这表明应变强化行为与应变率无关。

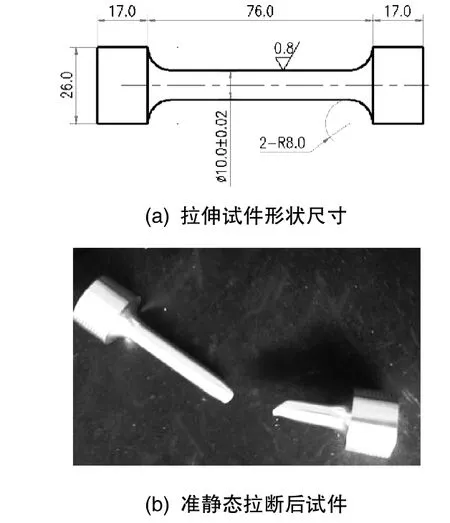
图1 拉伸试件形状尺寸及准静态拉断后试件

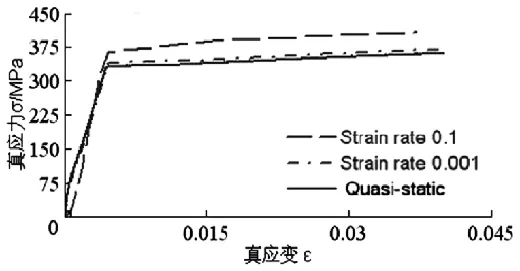
图2 三种拉伸速度下的真应力应变曲线

1.2 高应变率试验及结果

1.2.1 分离式霍普金森拉杆实验技术

汽车上某些零部件在塑性加工或碰撞等快速变形过程中，材料应变率较高[5]，其力学性能需要采用霍普金森拉杆实验装置进行测定，如图3所示。霍普金森实验原理是利用拉杆中一维弹性应力波理论以及弹性波透射、反射原理获得材料动态力学性能。实验中子弹以一定的速度沿轴向撞击输入杆，产生一个拉伸应力波脉冲εi并在杆中传播，试件在该应力脉冲的作用下发生高速变形，与此同时，在输入杆中产生往回的反射脉冲εr和输出杆中向前的透射脉冲εt。该实验技术是建立在两个基本假定基础上的。一个是一维假定，另一个是均匀假定。根据这两个假定可以计算得出试件中的工程应变率、工程应变和工程应力[6]：

式中C0、l0、E、A和A0分别为弹性波波速、试件初始长度、波导杆杨氏模量、波导杆截面积和试件初始截面积。真实应力σ、真实应变ε则可由下述关系式经工程应力和工程应变转换得到：

通过输入杆和输出杆上粘贴的动态应变片测得入射脉冲、反射脉冲及透射脉冲信号，经转换后即可获得材料在不同应变率下的应力-应变曲线。

图3 分离式霍普金森拉杆实验装置

1.2.2 高应变率试验及结果

高应变率试验试件为圆柱形哑铃状，两端通过螺纹与波导杆连接，在加工试件时，要保证中间段的加工精度。满足试件特定应变率下冲击拉伸试验，首先需要对冲击速度进行标定，本文中使用6个试件作为冲击速度标定样本。3个试件作为试验样本，并取3次试验结果的平均值作为最终试验结果。确定应变率为200s-1时子弹的冲击速度为8.2m/s，试件形状尺寸及拉断后如图4所示。

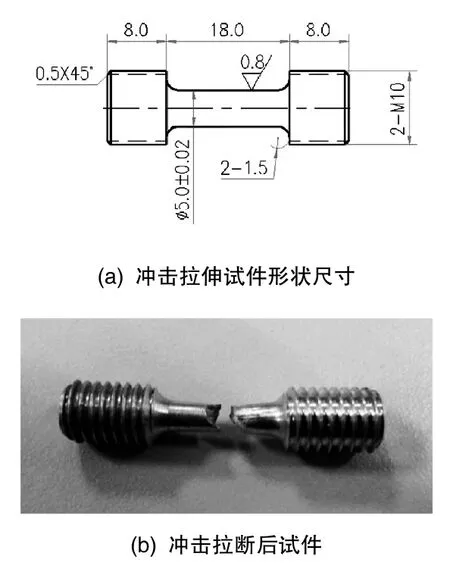
图4 冲击拉伸试件形状尺寸及拉断后试件

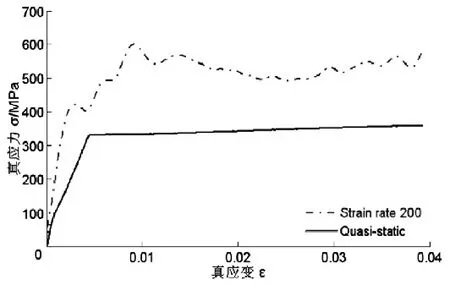
图5 高应变率下真应力应变曲线

常温下 5357铝合金试件在高速拉伸下其真实应力应变曲线如图5所示，图中曲线表明，材料的动态屈服应力随应变率增加而显著增大，应变率为200s-1时其值为492MPa，相对准静态屈服应力增加了48.7%。

2 5357铝合金本构模型及参数确定

2.1 Johnson-Cook模型

在粘塑性力学和连续损伤力学的基础上，考虑了金属材料的加工硬化效应、应变率效应和温度软化效应的J-C模型[7]由于形式简单，具有清晰的物理解释，且参数较少，在工程中得到了广泛的应用，该本构模型的表达式为：

在表达式(6)中，第一个括号里面主要反映了材料在变形过程中的屈服和加工硬化；第二个括号的内容考虑了应变率对动态屈服应力的影响；最后一个括号针对的是温度的软化效应。本文中各项试验都是在常温下进行，所以不考虑温度软化效应。因此J-C模型简化为：

室温、准静态下的J-C本构方程，不考虑应变率的影响，表达式(7)右边只剩下第一个括号的内容，两边同时取自然对数得到：

式(8)是以ln(σd-A)和lnε互为变量的直线方程，其中n为该直线方程的斜率，lnB为截距。A是材料的初始屈服极限，由实验测得为331Mpa。参数B和n可由试验数据拟合得到分别为1888Mpa和1.28。

在不同应变率试验结果的基础上，以 0.001s-1为参考应变率，然后将在不同应变下求得的参数C值取平均即为式(7)中参数C值，最终拟合得到的数值为0.0374。

将求得的各参数代入式(7)即可得到 5357铝合金材料的J-C本构模型：

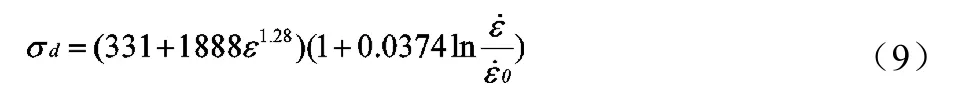
2.2 Cowper-Symonds模型

Cowper-Symonds模型[8]主要采用屈服应力比例缩放的方式，表达式为：

式中：σd为动态屈服应力；σs(εeff)由准静态拉伸试验处理得到的有效塑性应力应变曲线给定； 为应变率；C、p为与应变率相关的参数。

根据实验数据拟合得到各参数，在cm-ms-kg单位制下C为84.9，p为6.19，将参数代入表达式(10)即可得到5357铝合金材料的C-S本构模型为：

2.3 Plastic-Kinematic模型

Plastic-Kinematic模型是在经典弹塑性本构模型的基础上由Krieg和Key提出来的[9]，考虑了材料应变率的影响，分为等向强化、随动强化和混合强化3种类型，其表达式为：

式(12)中：Ep为塑性硬化模量，，其中E为材料的杨氏弹性模量，Et为材料单轴拉伸试验所得应力应变曲线的切线模量；σd为动态屈服应力；σ0为初始屈服极限；β为强化参数：β=0时为随动强化，β=1时为等向强化，0＜β＜1时为混合强化；εeff为有效塑性应变；C、p为与应变率相关参数。

根据试验数据拟合得到的 Plastic-Kinematic本构模型在cm-ms-kg单位制下为：

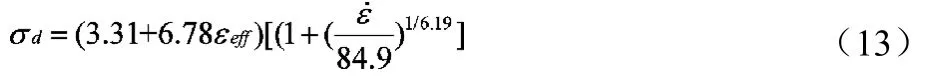
3 本构模型验证及仿真分析

3.1 有限元仿真模型

LS-DYNA是世界著名的通用显式动力分析程序，能够模拟现实世界中各种复杂的问题，特别适合求解各种二维、三维非线性结构的高速碰撞、爆炸和金属成型等非线性动力冲击问题，故本文采用LS-DYNA来进行有限元模型仿真分析。根据实际试件尺寸及霍普金森拉杆实验装置划分的有限元网格模型如图6所示：

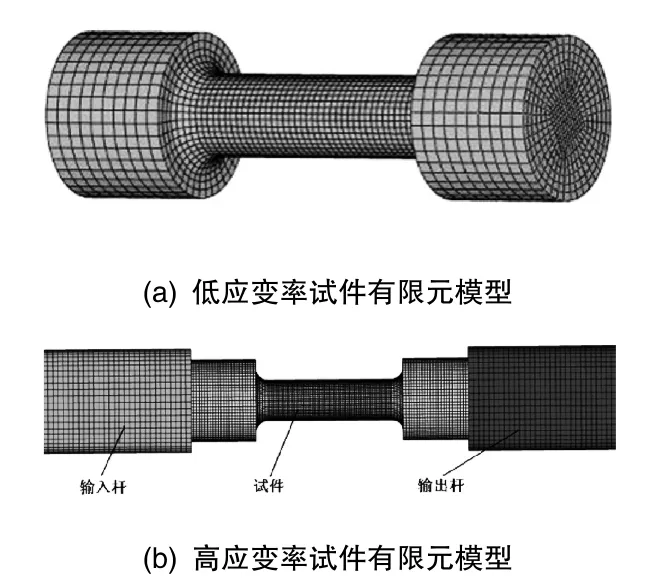
图6 试件的有限元模型

将试件分别采用不同的材料本构模型，把各参数输入材料模型卡片，参数如表2所示，然后导入LS-DYNA进行求解计算，并输出试件的应力应变曲线。

3.2 仿真结果分析

试件在不同应变率下由仿真计算得出的真实应力应变曲线与对应的试验曲线如图7所示。

图 7(a)为应变率 0.001s-1时三种模型计算结果与试验测量值的对比：图中可以看出C-S模型预测到的结果略高于试验测量值，而J-C模型和P-K模型预测的结果则要低于试验测量值，其中J-C模型预测的结果最小。总体来讲，在应变率为0.001 s-1情况下，三种本构模型均能较好地预测材料的力学行为，其中的C-S模型和P-K模型预测的结果与试验值更加接近。图 7(b)为应变率 0.1s-1时仿真计算与试验结果的对比：J-C模型的预测结果比试验测量值大，而其他两种模型较试验测量值小。总体来讲，在应变率为 0.1s-1时，三者的预测结果与试验测量值相差不大，都能较好地预测此应变率下材料的力学行为，在塑性强化开始阶段C-S模型和P-K模型更接近试验测量值，在强化中后段则是J-C模型更接近。图7(c)为应变率在200 s-1情况下，三种材料本构模型计算得到的结果与试验结果的对比：从图中可以看出试验测量值大于三种材料本构模型的预测结果，其中J-C模型预测结果大于其他两种模型，与试验测量值更加接近。

表2 材料模型卡片的参数

图7 仿真结果与试验结果对比

为了进一步定量地对比分析三种材料本构模型的计算结果与5357铝合金试验数据的相关性，本文选取试验和仿真获得的真实应力-应变曲线中的屈服极限应力 σy，切线模量Etan，及应变分别为 0.01、0.02和 0.03时刻对应的应力值σε0.01、σε0.02和 σε0.03进行分析。根据仿真和试验结果获得上述参数在不同应变率下的值如表3-表6中：

表3 试验得到的数值

表4 J-C模型计算得到的数值

表5 C-S模型计算得到的数值

表6 P-K模型计算得到的数值

引入单项误差分析表达式 Er(x)和总体相关指数 GCI对每种模型的仿真计算结果与试验测量值的相关程度进行定量分析[10]：

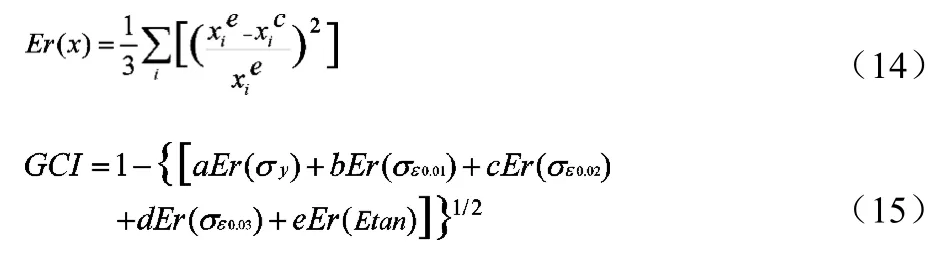
式(14)为三种应变率下材料模型的计算结果与试验测量值的相对误差取平方后的平均值，其中xie和xic分别为根据试验和仿真结果在应变率 0.001s-1、0.1s-1和 200s-1时取的参数数值。式(15)为综合五个参数的总体相关指数，其中a、b、c、d和e为权重因数，且a+b+c+d+e=1，本文中各权重因数都取为0.2。GCI值越大则模型的计算结果与试验数据吻合得越好，三种模型最终计算得到的GCI值见表7：

表7 三种材料模型的GCI值

从表7中可以看出， C-S与J-C模型的GCI值分别为0.8227和0.8241，二者相差较小，且要大于P-K模型的GCI值0.7737。表明C-S和J-C模型相比于P-K模型，能更好地模拟该铝合金的力学行为。从三者的本构方程中可以看出，在C-S模型中，其塑性阶段的应力-应变关系可由一个关于塑性应变的任意 σs(εeff)函数进行定义，在本文的仿真定义中，σs(εeff)是由准静态拉伸试验处理得到的有效塑性应力应变曲线直接输入。而在J-C及P-K模型本构方程中塑性应力-应变的函数关系则较为单一，如P-K模型中只能是一个以Ep为斜率的线性函数，J-C模型中则由B、n两个参数构造。因而，在塑性阶段的本构描述中，对试验结果描述的准确性由高到低应依次为C-S模型、J-C模型和P-K模型，与仿真预测结果一致。此外，在考虑应变率效应方面，P-K模型和C-S模型均采用了Cowper - Symonds应变率模型，而J-C模型则是利用应变率归一化后的结果对塑性阶段的应力进行缩放。两种应变率效应模型也有可能对本构模型的描述准确性造成影响，但从当前的研究结果中无法判断出哪一种应变率效应模型更适合模拟当前的铝合金材料。在LS-DYNA的MAT 15号材料中提供了这两种应变率效应模型的选择，在今后的研究可以利用该号材料模型对这两种应变率效应模型进行对比研究。

4 结论

对汽车碰撞吸能用 5357铝合金分别进行了准静态及应变率为0.001s-1、0.1 s-1和200 s-1下的单轴拉伸试验，发现该型号铝合金为应变率敏感材料。采用了J-C、C-S 和P-K等三种本构模型对该铝合金在不同应变率下的本构关系进行了描述，并根据试验数据拟合得出了各本构模型的参数。利用LS-DYNA进行了仿真分析，并引入总体相关指数GCI对各模型的仿真计算结果与试验数据的相关性进行定量分析，计算结果表明C-S、J-C及P-K模型的GCI值分别为0.8241、0.8227及0.7737，表明C-S与J-C模型的仿真结果与试验数据的相关性较高，且十分接近，二者相比于P-K模型能够更准确地模拟该铝合金在多种应变率条件下的力学行为。

[1] 郭伟国,田宏伟.几种典型铝合金应变率敏感性及其塑性流动本构模型[J].中国有色金属学报, 2009, 19(1): 56-61.

[2] 李娜,李玉龙,郭伟国.3种铝合金材料动态性能及其温度相关性对比研究[J].航空学报, 2008, 29(4): 903-908.

[3] 李春雷.2A12铝合金本构关系研究[D].哈尔滨:哈尔滨工业大学,2006.

[4] 林木森,庞宝君,张伟,等. 5A06铝合金的动态本构关系实验[J].爆炸与冲击, 2009, 29(3): 306-311.

[5] 陈贵江, 康永林, 朱国明, 等. 汽车用合金化镀锌深冲钢板动态变形行为[J]. 机械工程学报, 2010, 46(24): 10-15.

[6] 李建光,施琪,曹结东. Johnson-Cook本构方程的参数标定[J].兰州理工大学学报, 2012, 38(2): 164-167.

[7] Johnson G R, Cook W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C].Proceedings of the Seventh International Symposium on Ballistics,1983:541-546.

[8] HALLQUIST J O. LS-DYNA theory manual[R]. LSTC Inc., 2006.

[9] KEY S W, KRIEG R D A. Finite element computer procedure for the large deformation dynamic response of axisymmetric solids[J]. Com-puter Methods in Applied Mechanics and Engineering, 1974, 4(2):195-218.

[10] ZHU F, CHOU C C, YANG K H, et al. Calibrating material parame-ters to model the thin-walled components made of die cast AM60B magnesium alloy[J]. International Journal of Crashworthiness, 2012,17(5):540-552.