基于打分准则和改进PSO的基因选择方法

唐 迪，韩 飞+，程 准

(1.江苏大学 计算机科学与通信工程学院，江苏 镇江 212013；2.南京农业大学 工学院，江苏 南京 210031)

0 引 言

人类在探索疾病病理过程中发现通过分子角度能够更直观地掌握疾病的奥秘，在基因芯片基础上通过对基因表达谱数据进行挖掘为疾病的诊断和治疗提供了新的重要途径[1]。研究结果表明，肿瘤的治病基因通常为少量的几个至几十个，而微阵列数据高维小样本的特点成为筛选致病基因的巨大挑战[2]。肿瘤分类过程中基因选择和特征选取起着举足轻重的作用[3]。随着研究的深入，进化算法逐渐被引用到基因选择中来，如遗传算法、模拟退火算法、蚁群算法和PSO算法等。相比于其它算法，PSO算法简便、高效，易于收敛于全局最优解的优点使它受到大量学者的青睐。Kar等[4]提出了一种PSO结合K近邻法的方法来筛选白血病和小圆蓝细胞癌的基因子集；Barnali等[5]利用K-均值聚类、信噪比(SNR)给基因分级，收集得分最高的基因输入PSO生成最优基因集合，并用SVM、KNN、PNN作为评价器，采用留一法交叉验证；Vieira等[6]采用MBPSO结合SVM来对败血病进行死亡预测，MBPSO利用速度和最优解之间的相似度控制种群变异，利用SVM对内核参数同时进行优化。然而这些方法在PSO算法的应用过程中都存在算法易于陷入局部最优解的缺陷，对基因选择产生了很大影响。为了有效解决基因数据表达谱的维数灾难问题，提高基因的分类性能，本文提出了一种高效的基因打分准则，可以大量删减冗余基因，并让保留基因对于分类的作用最大化；为了解决PSO算法易收敛于局部最优解的缺点，本文通过半初始化和Metropolis准则对算法进行优化；利用ELM极限学习机[7]作为评价基因子集分类正确率的分类器，得出算法分类性能的量化数据。实验结果表明，本文所述方法筛选出的基因子集对疾病亚型分类具有高准确性。

1 相关技术

1.1 PSO算法

微粒群算法(particle swarm optimization，PSO)提出了一种模仿鸟类的群体行为的智能算法模型[8,9]。粒子相当于鸟群中的一只小鸟，每个粒子有各自的飞行方向和飞行速度，粒子在飞行过程中寻找最优解，每个粒子把飞行过程中得到的最优解进行比较得到粒子历史最优适应度值，同时粒子之间共享信息，将所有粒子得到的历史最优适应度值进行比较，从而得到全局最优解。在飞行过程中粒子的速度和位置更新公式为

vij(t+1)=ωvij(t)+c1r1j(t)(pij(t)-xij(t))+
c2r2j(t)(pgj(t)-xij(t))

(1)

xij(t+1)=xij(t)+αvij(t+1)

(2)

其中，i表示第i个粒子，j表示粒子的第j维，t表示第t次迭代，ω为惯性权重，c1，c2表示学习参数，r1，r2为[0,1]间两个相互独立的随机数，vij(t)表示第i个粒子第j维第t次迭代后的位置；xij(t)表示第i个粒子第j维第t次迭代后的速度；pij(t)表示第i个粒子第j维第t次迭代后的个体最好位置；pgj(t)表示第j维第t次迭代后的群体最好位置。

1.2 模拟退火算法的Metropolis准则

模拟退火算法(simulated annealing，SA)是由N.Metropolis等提出的一种概率算法[10]。固体中的粒子在温度升高到足够温度时进行无规则运动，随着时间流逝温度逐渐降低，粒子在每个温度下逐渐趋于有序，并在该温度条件下达到平衡，模拟退火算法正是模拟这种退火原理[11,12]。材料在不同状态时粒子具有不同的能量，设在状态i下的能量为E(i)，进入状态j时能量为E(j)，通过粒子能量的变化定义材料状态的改变:

(1)如果E(j)≤E(i)， 接受该状态被转换。

(2)如果E(j)>E(i)， 是否接受该状态转换由概率值决定。

接受较差状态的概率值P(dE)与温度T以及能量差dE有关

P(dE)=exp(dE/KT)

(3)

其中，K是一个常数，exp表示自然指数。dE<0，因此P(dE) 的值在[0,1]之间。从函数角度看概率公式为单调递增函数，随着温度的增大，出现状态转换的概率也随之增大。历史最优解优于当前适应度值使得状态受困于局部最优解，通过使用Metropolis准则增大了跳出局部最优解的可能性。并且经过数学家的严格证明，在条件满足情况下(温度够高，降温过程足够慢时)逼近全局最优解的概率接近100%[12]。

2 改进方案

2.1 基于打分准则的基因选取

本实验采用的基因表达谱数据中每个样本含有几千个基因，迄今为止的研究无法确认每个基因的具体作用，对于某一种疾病不是所有基因都是致病基因，因此当针对某种疾病时，删除冗余基因为疾病的诊断治疗节省了大量资源。利用分类信息指数(information index to classification，IIC)[13]进行基因粗提取，删选出200到400个基因。在基因粗提取的基础上，本文设计了一种打分准则来评价这些基因。随机抽取粗提取得到的基因进行组合，对这些随机抽样得到的基因组合利用打分准则进行打分，并依据分数由高到低排序，筛选出分数较高的有效基因。

有效基因筛选步骤如下：

(1)预设基因个数m为每个基因集合所包含的基因数量，随机生成一个基因集合矩阵，该矩阵由α个基因集合构成；

(2)计算每个基因集合的适应度值，适应度函数的公式为

fitness(i)=100-100*cvaccuary(i)

(4)

其中，cvaccurary(i)表示第i个粒子在验证集上的ELM分类准确率；

(3)计算所有基因集合的适应度值，设置一个适应度阈值Q，筛选出(1)中小于Q的基因集合，将这些集合按照适应度值的大小进行排序，作为有效的基因评价集合；

(4)对有效的基因评价集合中存在的所有基因进行打分

在两个方面对每个基因进行打分：

从基因集合1：基因集合α循环执行

1)score1

若该基因集合含有此基因

score1=score1+α-R

其中，R为该集合按适应度值的排名

若该基因集合不包含有次基因

score1=score1+0

2)score2

若该基因集合含有此基因

score2=score2+1

若该基因集合不包含有此基因

score2=score2+0

根据上述方法计算出所有基因的score1和score2,并对所有基因的score1和score2进行归一化处理，得到S1和S2。则第i个基因的最终得分为Score(i)=S1(i)+S2(i)；

(5)根据每个基因的最终得分由高到低排序，选取得分较高的前40个基因，将这些基因称为有效基因。

2.2 PSO算法改进

2.2.1 粒子新定义

在本文采用的PSO算法中的每一个粒子都是一个1×(m+1)维的向量，其中m是打分准则中设定的基因个数，每一维有各自的位置和速度，互不干扰，并在迭代过程中不断更新。第一维表示最优基因子集包含的基因数,其余m维分别表示该维选择的基因，即2到m+1维中的基因是该维选择的最优基因，基因序号不重复，如若有重复选择的基因，删除所有重复的维数，只保留1维，删除维数的基因由该维重新筛选，这m维基因表示该粒子筛选的最优基因子集。

2.2.2 算法改进

PSO算法易于陷入局部最优解是目前学者一直致力于研究和解决的问题，本文针对PSO算法的不足提出了如下改进方案：

(1)半初始化

粒子陷入局部最优解时将部分粒子进行初始化，可以从根本上改变粒子在全局最优解的比较过程中的局限性，本文设定将一半粒子进行初始化。当PSO算法陷入局部最优解时，出现多代不更新的情况(最新一次迭代的适应度值低于历史最优值即为一次未更新)，设定阈值μ0，当μ0次未更新时，随机选取一半的粒子进行初始化。迭代过程中重复判断更新过程，直至跳出局部最优解。

(2)引入模拟退火算法的Metropolis准则

为了有效避免粒子群的早熟现象，引入模拟退火算法的Metropolis准则，以一定概率接收比当前最优解差的适应值。在第i+1次粒子迭代时的最优值Pbest的更新公式如下：

当f(Xi+1)-f(Pbest(i))≥ε时

Pbest(i+1)=Xi+1

(5)

T的更新准则为

(6)

其中，T0和Tend分别为T的初始值和最终值；Imax为最大迭代次数，I为当前迭代次数。

(3)提高算法效率

在医疗领域，时间就是生命，为了减少算法时间，提高算法效率，本文提出了预判的思想。在计算历史最优解与全局最优解之前，将每个粒子的适应度值直接与输出条件进行比较，若满足条件则再次计算进行验证，若通过验证则直接输出该粒子筛选的基因子集。具体步骤为：

每个粒子的适应度值FZ是两次计算该粒子筛选的基因子集的分类准确率后求取的平均值。

1)若FZ≤FMin(FMin是已设置好的最小适应度值)，则再计算20次样本随机初始化5折CV错误率，若20次的均值AVG≤FMin，则输出该粒子筛选的基因子集，并终止运算过程。

2)若FZ>FMin，那么该粒子的适应度值FZ由后20次计算所得的均值替代。

2.3 基于打分准则和改进的PSO算法的基因选择方法

本文结合打分准则和改进的PSO算法提出了一种基因选择方法。利用打分准则删除冗余基因并筛选出对疾病起重要作用的部分基因，利用模拟退火算法的Metropolis准则使PSO算法易于跳出局部最优解。具体步骤如下：

步骤1 载入原始基因数据集，并分成训练集和测试集；

步骤2 利用分类信息指数进行基因粗提取。采用过滤的方式筛选出200～400个基因。再将训练集和测试集进行下面的实验；

步骤3 利用打分准则进行基因评价，并筛选出有效基因集合。通过章节2.1的打分准则筛选出得分最高的前40个基因作为有效基因集合；

步骤4 PSO初始化。初始化所有的参数，粒子的速度和位置；

步骤5 根据式(4)计算每个粒子的适应度值Fg、全局适应度值Fz,并将Fg和Fz设为当前最优解；

步骤6 扰动c1c2，更新速度，更新位置；

步骤7 计算新的粒子最优适应度值g，全局最优适应度值z。利用式(5)和式(6)选出当前历史最优解(包括每个粒子的最优解Fg，以及全局最优解Fz)；

步骤8 判断是否符合实验条件：I≤IMax，FZ≤FMin,(FMin为设定的适应度函数阈值)若符合，则输出基因子集及适应度值，否则继续执行步骤9；

步骤9 判断更新计数器。若不更新次数θ>μ0，则选择一半的粒子，并随机重新生成这一半的粒子，跳到步骤5继续实验。

3 实验结果与讨论

本文的实验对象是两个公开的微阵列数据集，分别为SRBCT数据集和Brain cancer数据集，SRBCT数据集是一个多类数据集，Brain cancer数据集是目前较为难分的两类数据集，通过在这两个数据集上的实验来验证本文所提方法的可行性。

3.1 数据集

儿童小圆蓝细胞癌(SRBCT)数据集是多类数据集，共包含83个样本，分为4类，其中每个样本有2308个基因。 分别为29个ewing faming of tumors(EWS)样本，25个rhabdomyosarcoma(RMS)样本，以及11个burkitt lymphoma(BL)样本，neuroblastoma(NB)样本18个。在网站http://www.biomedcentral.com/content/supplementary/1471-2105-7-228-S4.tgz上可以下载该数据集。

脑癌(Brain Cancer)数据集包含60个样本，分为两类：46个patients with classic样本和14个patients with desmoplasticyangben。每个样本包含7219个基因，数据集来源于http://linus.nci.nih.gov/～brb/DataArchive_New.html。

3.2 实验结果

通过在两个数据集上的多次实验选出了高分类性能的基因集合。在本文中，ELM被用作分类器来评价通过本文方法选出的两个数据集的基因集合，对每组集合重复运行200次计算相应的准确率并求取均值，实验结果见表1。

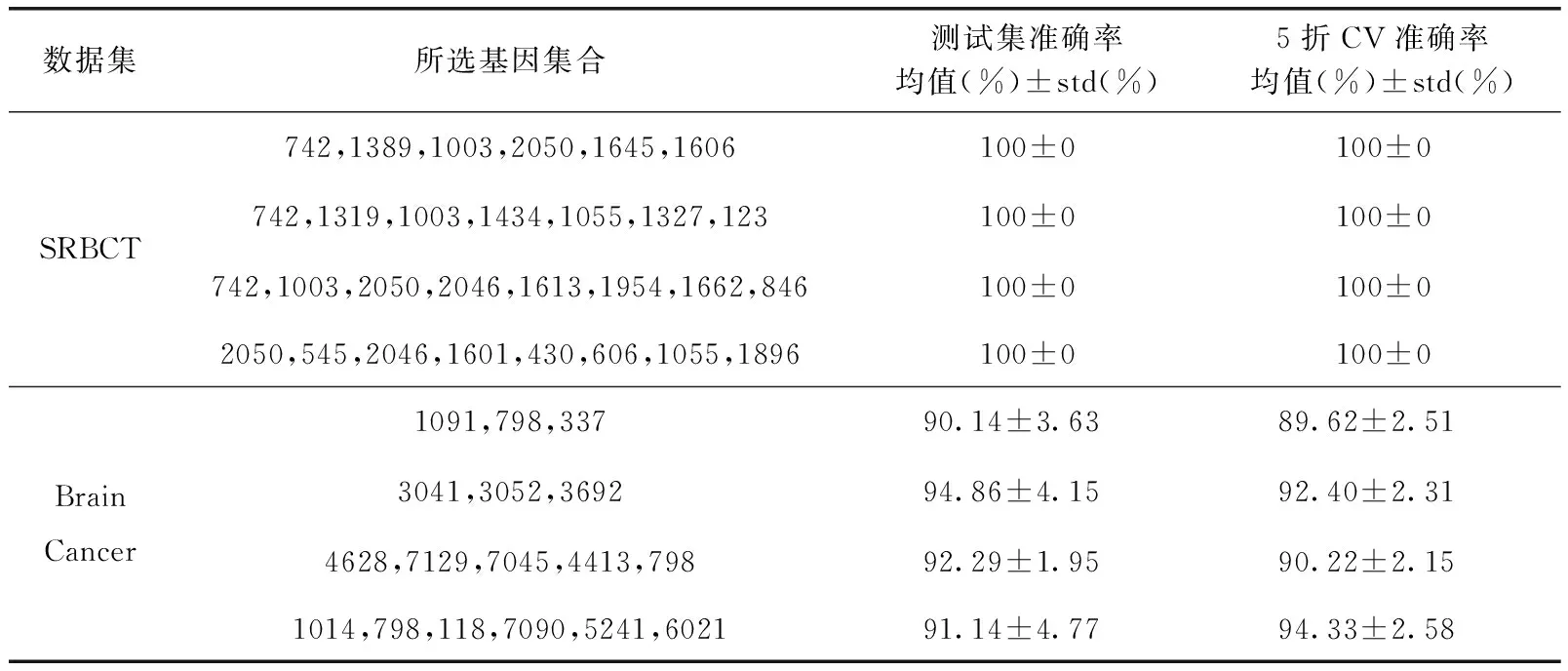
表1 两个数据集在不同基因集合上的ELM分类准确率

从表1可以看出，对于SRBCT数据集，所有选出的基因集合在ELM上的测试集准确率为100%，5折CV正确率达到100%，对应的基因集合最少只包含6个基因，最多包含8个基因。对于Brain Cancer 数据集，选出的包含3个基因的基因集合测试集正确率高达94.86%，5折CV正确率为92.40%，包含6个基因的基因集合的5折CV正确率高达94.33%。这些高准确率的基因集合验证了本文方法的正确性。

分别对SRBCT数据集和Brain Cancer数据集进行500次独立重复的实验，选出的基因集合中出现基因频次最高的10个基因，其表现内容见文献[12]。

对于SRBCT数据集，本文方法所选的高频次基因812105、基因796258、基因325182、基因1435862、及基因624360都曾被其它文献选出过，其中除基因624360外其它4个基因均被多个文献选中。对比表1中的基因集合，基因812105和基因796258在4个具有高分类性能的集合中出现了3次，表明该基因在SRBCT数据集的亚型分类中起到重要作用。

对于Brain Cancer数据集，基因M64934、基因AB000895、基因HG3033-HT3194 at、基因M96738、基因X87159及基因U65676都在文献[16]中被选出，基因M65254和基因AB000895也被文献[15]选中。

两个数据集中的多个基因被多个文献选中，证明这些基因在基因分类中的重要作用。利用频率前10的基因得到数据集SRBCT和数据集Brain的热点图，可以更直观地看到每个基因对于分类的作用效果，如图1所示。

从图1中可以看出，对于SRBCT数据集多数基因的表达水平都能够清晰的将4种亚型清晰地区分出来，如编号255、123、545的基因，但基因亚型的划分总体依靠多个基因的表达水平来共同区分，验证了SRBCT数据集并不是依靠单个特殊基因来划分的，而是依靠多个基因的共同作用。对于Brain Cancer数据集，可以看出没有任何一个基因可以独立将两类亚型划分，原因在于一些基因过表达的现象。

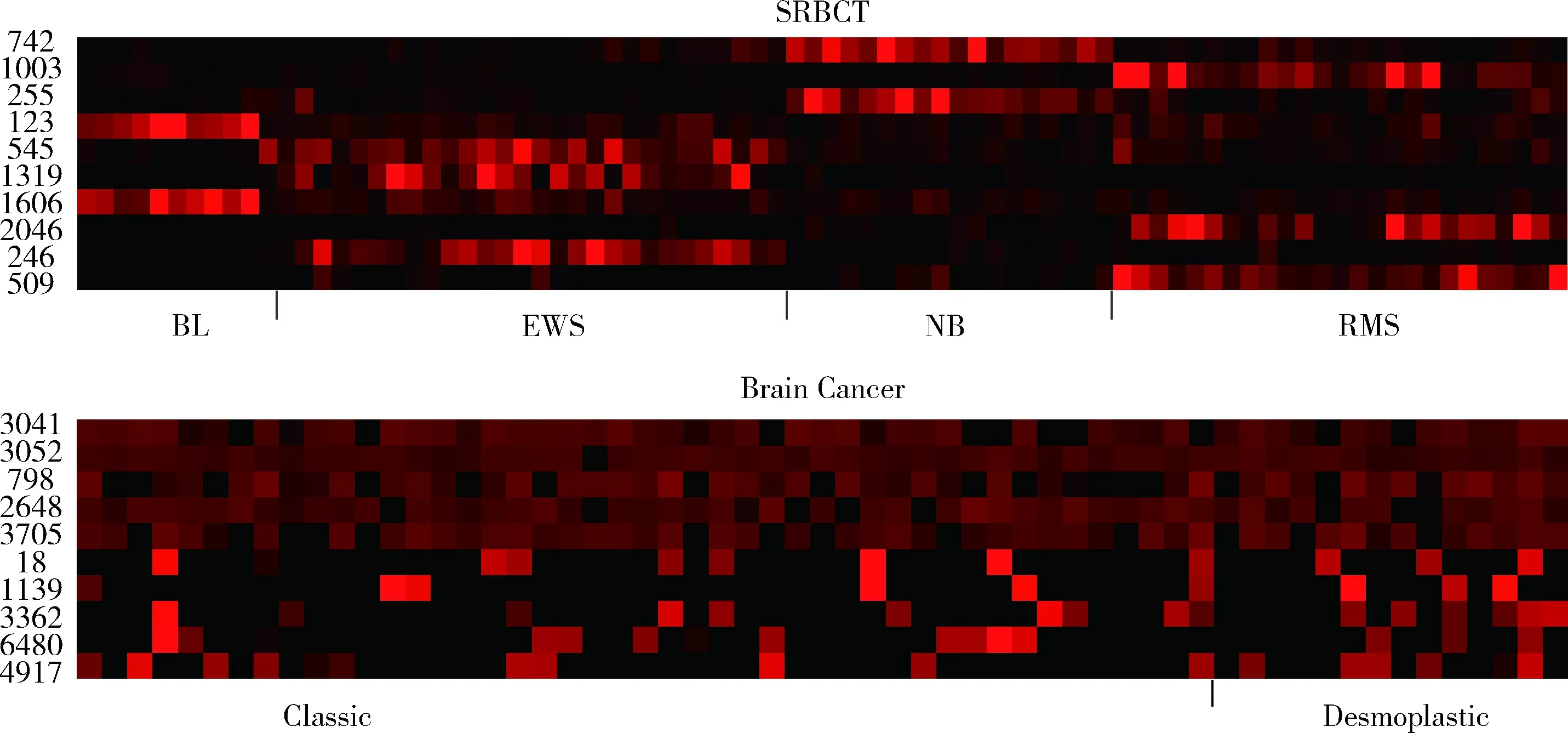
图1 两个数据集上选取频次最高的10个基因的热点

3.3 与其它方法的比较

为了进一步验证本文方法的可行性，将本文结果同其它4种方法进行对比。这4种方法均是利用ELM作为分类器。BPSO-ELM和KMeans-BPSO-ELM未对原始数据进行预处理，KMeans-GCSI-MBPSO-ELM[16]和BPSO-GCSI-ELM[15]加入了先验信息对初始基因进行了粗提取。将本文方法重复进行100次实验，分别求取在两个数据集上的5折CV分类准确率的均值，与其它方法的对比结果见表2。

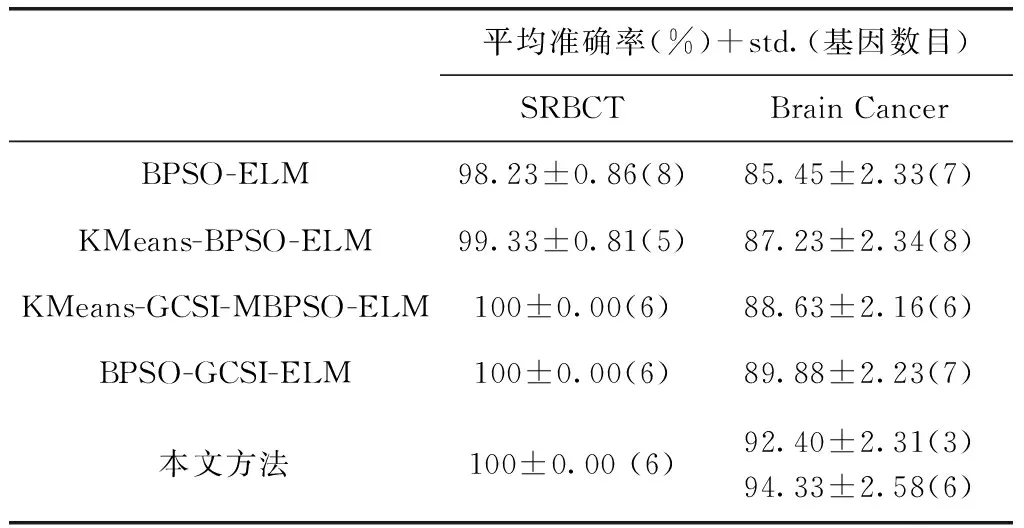
表2 5种不同方法在两个数据集上的5折CV分类准确率

表2中的5种方法都具有较高的准确率和较低的冗余度，在两个数据集上，BPSO-ELM和KMeans-BPSO-ELM相比其它3种方法结果较差，原因在于BPSO-ELM缺少预处理存在大量冗余基因干扰了选择，KMeans-BPSO-ELM利用聚类方法并不能起到删除冗余的效果。本文方法相比KMeans-GCSI-MBPSO-ELM和BPSO-GCSI-ELM这两种加入先验信息的方法在Brain Cancer数据集上效果有明显提高，表明本文的基因预处理方法以及对于PSO算法的改进更加有效。

4 结束语

(1)本文提出了一种基于打分准则和改进PSO算法的基因选择方法。该方法在IIC分类信息指数的基础上，利用抽样调查的科学性随机生成基因集合，利用自定义的打分准则对集合中的每个基因打分、排序；筛选出与样本分类密切相关的基因。

(2)利用模拟退火算法中的Metropolis准则，改进PSO算法，使得该算法能以一定概率跳出局部最优解；设置更新阈值μ0，当超过μ0次粒子不更新时半初始化粒子；然后结合ELM计算分类的准确性从而得到最优的基因子集。

(3)实验结果显示通过本文方法选出的基因集合基因个数少，分类准确率高。对于SRBCT数据集，选出的基因子集仅包含6个基因，5折CV准确率高达100%，对于Brain Cancer数据集选出最少包含3个基因的基因集合，5折CV准确率高达92%。但本文方法需要提前设定基因数目进行实验，作者将在以后的研究中进一步改进算法来自适应获得最优的基因数目。

[1]RK Singh,Sivabalakrishnan M.Feature selection of gene expression data for cancer classification:A review[J].Procedia Computer Science,2015,50:52-57.

[2]HUANG Deshuang.Research on gene expression data mining[M].Beijing:Science Press,2009(in Chinese).[黄德双.基因表达谱数据挖掘方法研究[M].北京:科学出版社,2009.]

[3]Wang Y,Fan X,Cai Y.A comparative study of improvements pre-filter methods bring on feature selection using microarray data[J].Health Information Science and Systems,2014,2(1):1-9.

[4]Subhajit Kar,Kaushik Das Sharma,Madhubanti Maitra.Gene selection from microarray gene expression data for classi-fication of cancer subgroups employing PSO and adaptive K-nearest neighborhood technique[J].Expert Systems with App-lications,2015,42(1):612-627.

[5]Barnali Sahu,Debahuti Mishra.A novel feature selection algorithm using particle swarm optimization for cancer microarray data[J].Procedia Engineering,2012,38(5):27-31.

[6]Vieira SM,Mendonca LF,Farinha GJ,et al.Modified binary PSO for feature selection using SVM applied to mortality prediction of septic patients[J].Applied Soft Computing,2013,13(8):3494-3504.

[7]Ding S,Zhao H,Zhang Y,et al.Extreme learning machine:Algorithm,theory and applications[J].Artificial Intelligence Review,2015,44(1):103-115.

[8]LI Rongjun,LIU Xiaolong.Particle swarm optimization algorithm based on microbial behavior mechanism[M].Guangzhou:South China University of Technology Press,2015(in Chinese).[李荣军,刘小龙.基于微生物行为机制的粒子群优化算法[M].广州:华南理工大学出版社,2015.]

[9]Chen SM,Chien CY.Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques[J].Expert Systems with Applications,2011,38(12):14439-14450.

[10]Ingber L.Adaptive simulated annealing[J].Intelligent Systems Reference Library,2013,35(5):491-500.

[11]Junior H,Ingber L,Petraglia A,et al.Adaptive simulated annealing[J].Intelligent Systems Reference Library,2012,35(5):33-62.

[12]TANG DI.A Study of gene selection method based on scoring criterion and particle swarm optimization[D].Zhenjiang:Jiangsu University,2017(in Chinese).[唐迪.基于打分准则和微粒群算法的基因选择方法研究[D].镇江:江苏大学,2017.]

[13]Khan J,Wei JS,Ringner M,et al.Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks[J].Nature Medicine,2001,7(6):637-679.

[14]Kar S,Das Sharma K,Maitra M.Gene selection from microarray gene expression data for classification of cancer sub-groups employing PSO and adaptive K-nearest neighborhood technique[J].Expert Systems with Applications,2015,42(1):612-627.

[15]Han Fei,Yang Chun,Wu Ya-Qi.A gene selection method for microarray data based on binary PSO encoding gene-to-class sensitivity information[J].IEEE/ACM Transactions on Computational Biology and Bioinformatics,2015,14(1):1.

[16]Han F,Sun W,Ling Q-H.A novel strategy for gene selection of microarray data based on gene-to-class sensitivity information[J].PLoSONE,2014,9(5):e97530.

[17]Chu F,Wang L.Applications of support vector machines to cancer classification with microarray data[J].International Journal of Neural Systems,2005,15(6):475-484.