基于外存的概念格维护算法

王春月，王黎明，张 卓

(郑州大学 信息工程学院，河南 郑州 450001)

0 引 言

在实际应用中，生成概念格[1-3]的形式背景随着时间的推移会发生变化，此时原始概念格的结构也会改变。目前已经有许多概念格的维护算法[4-7]，这些传统的算法适用于计算环境的内存大小不受限制的情况下使用。随着形式背景的规模不断增长，概念格的传统维护算法对于内存需求呈指数增加。内存的增长速率无法赶上数据量的增长，这势必会导致内存不足的情况出现。针对内存不足问题，超内存概念格的维护可以采用外存算法解决。外存算法是指由于数据规模太大导致无法一次性装入内存，此时需借助外存的反复读写数据的算法。例如，文献[8,9]在LOD技术基础之上提出一种数据分块与内外存调度策略相结合的数据处理算法，它们将大规模数据采用四叉树、二叉树或分片标记的分割方式将数据分块，然后采用LRU内外存调度算法释放内存中近期不使用的块，并从外存中调入所需块，从而减少了内存的开销，提高了大规模数据绘制的实时性。文献[10]提出一种基于外存后缀树的top-k字符串局部比对算法，该算法依次从磁盘中读取原字符串的后缀树的各子树，深度优先遍历子树并根据子树的维护信息从内存和磁盘中分别找到参与局部对比的子串、计算比对结果。该方法从根本上消除了内存空间对于算法的束缚。

因此本文以形式背景中对象与属性之间的二元关系消减情况为应用背景，提出了一种基于外存的超内存概念格维护算法，该算法以概念簇为基本单位划分大规模概念格，并将划分后得到的小规模概念块依次读入内存中进行迭代处理，最终得到完备概念格的方法。该方法能够通过设置概念块的大小，达到充分利用内存，减少外存的访问次数的目的。本文算法能够在有限的内存资源下，借助外存的大容量空间，实现超内存概念格的有效维护，并且能够辅助超内存概念格完成具体的应用。

1 相关定义

本节针对概念格内外存调度维护算法的相关定义进行详细介绍，对于二元关系消减理论参见文献[11]，本节对文献[11]中节点类型进行形式化的表述。即受影响的节点、保留节点、减对象节点、减属性节点、分割节点以及删除节点,分别用ES(K)、RS(K)、OS(K)、AS(K)、PS(K)与DS(K)表示。

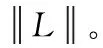
定义2 概念簇：如果C∈ES(K)，那么C节点与其父节点Parent(C)和子节点Child(C)统称为概念簇，记作Cluster(C),C称为聚集中心。

定义3 概念块：在L(K)中，如果存在n个受影响的节点，首先将这n个节点按外延基数升序排列，然后将此序列分割成m个子序列，前m-1个序列中节点个数均为α，其中m<=n，最后得到每个子序列中各个节点的概念簇，最终得到m个概念块，记作Block。

定义4 父基节点：如果对于∀C∈RS(K),存在某个节点C′∈AS(K)∪DS(K),满足C′C且Int(C)=Int(C′)-{m},则称C节点为C′的父基节点，记作fBase(C′)。

定义5 子基节点：如果对于∀C∈RS(K),存在某个节点C′∈OS(K)∪DS(K),满足CC′且Ext(C)=Ext(C′)-{g}, 则称C节点为C′的子基节点,记作cBase(C′)。

定义6 辅助节点：对于∀C∈Blocki，i=1,2,…,n且C为聚集中心，其中n表示概念格划分的概念块数。如果C存在父基节点或子基节点，那么Child(fBase(C))与Parent(cBase(C))统称为Blocki的辅助节点。

2 概念格内外存调度维护算法

本文以消减形式背景中单个对象与属性之间的二元关系的情况下维护原始概念格为应用背景，研究当传统算法在有限的内存资源下维护概念格失效时，解决如何借助外存空间实现规模数据的有效维护问题。

2.1 理论基础

本节根据父子节点的类型对二元关系消减理论中边的更新过程进行优化，从而提高规模数据的维护效率。二元关系消减理论中节点的映射规律仍保持不变。根据父子节点的类型边可能会有25种情况，下面通过讨论哪些边的情况不存在，从而减少不必要的遍历，降低算法的时间复杂度。

定理1 如果C′∈OS(K),如果C=(A,B),使得C′C成立，则C必然满足下列两种情况之一：①C∈RS(K),且C为父基节点；②C∈OS(K)。

证明：设C1=(A1,B1)为C′的父基节点，则B1=B′-{m}。

(1)由于C′C且C∈RS(K)，则B⊆B′且m∉B，因此B⊆B′-{m}=B1⊆B′, 若C≠C1,有C′C1≤C, 故C′C不成立。

(2)由于CS(K)=RS(K)∪OS(K)∪AS(K)∪PS(K)∪DS(K)和(1),只需证明C∉AS(K)∪PS(K)∪DS(K)即可。用反证法，假设C∈AS(K)∪PS(K)∪DS(K), 因C′C,故Ext(C′)⊆Ext(C)。 得到Ext(C′)-{g}⊆Ext(C)-{g}=Ext(cBase(C))， 因此cBase(C)节点与C′节点存在交集Ext(C′)-{g}， 此时与AS(K)、PS(K)、DS(K)的定义相矛盾，所以假设不成立。

由定理1可知，减对象节点的父节点只有两种情况：唯一的保留节点(父基节点)或减对象节点。

定理2 如果C′∈AS(K)，如果C=(A,B), 使得CC′成立，则C必然满足下列两种情况之一：

(1)C∈RS(K),且C为子基节点；

(2)C∈AS(K)。

证明：由于概念格内涵与外延的对偶性，由定理1同理可证该定理的正确性。

定理2说明，减属性节点的子节点只有两种情况：唯一的保留节点(子基节点)或减属性节点。

根据定理1～定理3以及文献[11]的命题2、命题3可知，如表1所示有7种边的情况不存在。

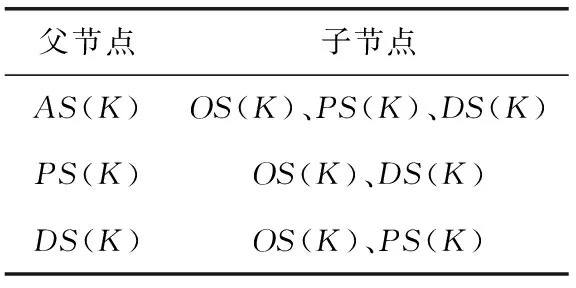
表1 父子间边关系不存在的情况

定理3 在L(K)中,∃C1,C2∈ES(K) 且C1C2,若在L(K*)中C1=(A,B-{m})，C2=(A-{g},B), 则在L(K*)，C1C2不成立。

证明：反证法，因为C1∈ES(K)， 所以g∈A。假设在L(K*)中，C1C2成立，则存在Ext(C1)⊆Ext(C2)， 与条件矛盾，所以假设不成立。

由定理3说明，原始概念格中若父节点在L(K*)中更新为内涵不变，外延减g对象的节点，而子节点更新为外延不变，内涵减去m属性的节点，则原始概念格中的父子关系在新概念格中不成立。满足以上情况的边见表2。

表2 满足定理3情况的边

因此以上情况的边在概念格的维护过程中需要删除，为了保证格的偏序关系还要判断父节点与子节点的子节点以及子节点与父节点的父节点是否存在直接的前驱后继关系，若存在则新增边。由文献[11]命题2可知，此时需要遍历所有的子节点和所有的父节点，而根据定理1、定理2可知可以根据父子节点的类型，减少不必要的比较，具体比较方式如图1所示。

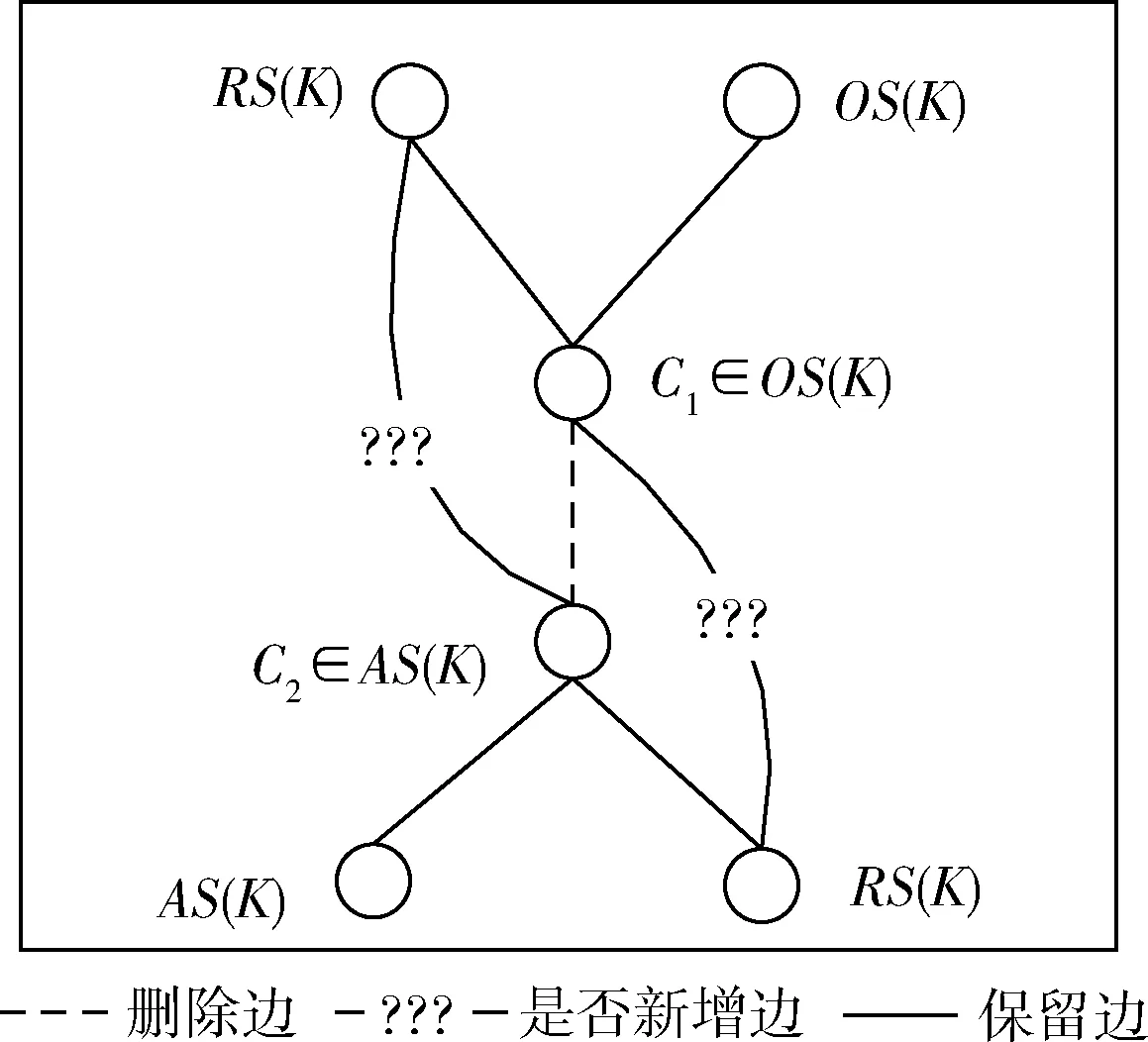
图1 在L(K*)中，减对象-减属性边关系的变化规律

由定理1、定理2可知，C2的子节点与C1的父节点类型如图1所示。再由定理3可知，在L(K*)中，C2与C1的OS(K)父节点以及C1与C2的AS(K)子节点不存在直接前驱后继关系，因此它们之间不用新增边，故C1减对象节点与C2减属性节点间边关系删除时仅考虑两条边关系是否增加，即fBase(C1)与C2以及cBase(C2)与C1。若Ext(fBase(C1))与Parent(C2)-C1集合中任意节点的外延都不存在包含关系，fBase(C1)与C2新增边。同样若Ext(cBase(C2))与Child(C1)-C2集合中任意节点的外延都不存在包含关系，则cBase(C2)与C1新增边。这样只需记录节点的父基节点与子基节点即可，从而减少遍历C1的父节点与C2的子节点，提高边更新效率。表2中其它边的变化规律同样依据父子节点的类型，如图2所示。

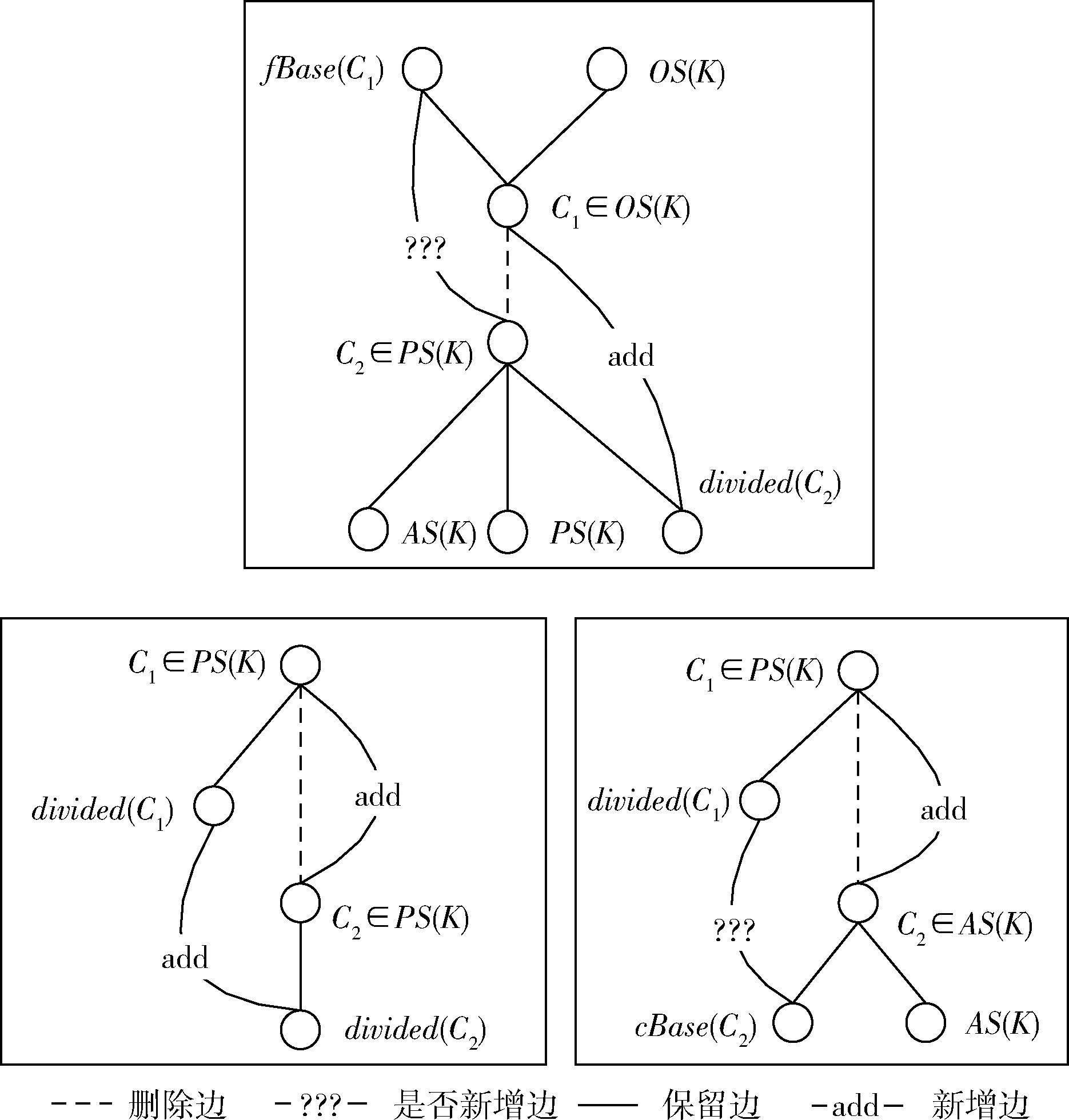
图2 在L(K*)中，表2其余边关系的变化规律

由文献[11]定义4可知，分割节点C在新概念格中被分割成两个节点，此处重新定义两个节点的形式化表示，即分割成C与divided(C)两个父子节点。除了表2的边关系需要删除外，删除节点与其父子节点的边同样需要删除，变化规律遵循文献[11]的规律。总之，根据以上边和节点的变化规律更新原始概念格就可以得到新的完备格。

2.2 内外存调度策略

外存算法通过利用大容量的外存空间，将暂时不需要的数据存到磁盘中，当需要的时候再调入内存，对数据进行分块处理，从而实现在一个小的内存空间上运行一个比它大的规模数据。此时算法的性能主要取决于I/O读写数据块的次数，故本文算法在设计上要尽量减少磁盘I/O的操作。本节将二元消减理论与概念格特性相结合，设计合理分块方式和内外存调度策略以此实现超内存的概念格的维护。

2.2.1 分块技术

在形式概念分析的实际应用中，为达到块内高内聚，块间低耦合的目的，需要受影响的节点与其父子节点尽量在同一块中，即基于定义2的概念簇为单位划分概念块使得分块的质量变高。按照定义3方式划分概念格，使得部分无用的保留节点不必读入内存中，从而减少I/O读写次数与内存资源的消耗。同时按受影响的节点的外延升序排列，保证了子节点一定先于父节点处理，在算法设计中为找到表2中的多种情况，当前节点只需要遍历子节点即可，若父节点与当前节点之间存在表2情况，等到处理该父节点时在处理该边的情况，这样可以简化算法处理流程。

概念块的大小影响算法的性能，随着概念块内节点数的增加，块处理的时间/空间需求增大，为了保证块的处理效率，块中节点数不宜过多，反之太少，又会增加内外存读写次数。因此概念块大小的设置取决于主存空间的大小。

2.2.2 调度算法

在形式概念分析应用中，通常利用概念节点与节点之间的层次关系解决实际问题，此时对于概念节点的遍历过程通常采用自底向上或自顶向下的广度优先或深度优先的方式遍历概念格的节点。为契合概念格的应用过程本文的算法采取自底向上的方式依次处理各个概念块，同时为避免相邻两块中重复节点的多次读取，概念节点增设使用频率域count，设置count的原则是如果当前节点类型为C∈AS(K)∪PS(K)， 若其k个父节点不是Blocki中要处理的受影响节点，则置C的count域为k，如果C∈AS(K) 还需要将Parent(C)、cBase(C)的使用频率count加上k值，如果C∈PS(K)将divided(C)节点count域加上k值。

基于上述概念块的处理顺序以及块间节点的关系，本文采取最近最少使用(LRU)调度策略：即当Blocki概念块处理过后若块中的节点不会在Blocki+1块中使用(即count域值为0)，则将这些从内存中释放，其余节点保留在内存中用于Blocki+1块中节点的处理，这样可以减少两个概念块中重复节点的读取次数，降低I/O量。

2.3 算法描述

BlockLattice算法按照LRU调度策略逐个处理概念块。每个概念块的维护包括3个主要过程：①读入内存，即将概念块中不在内存中的概念节点读入内存中等待进一步处理。②处理概念块，判断概念块中每个受影响节点的具体类型，然后根据父子节点的类型更新边，在维护过程中将不在内存中的辅助节点信息读入内存中。③写入外存，即将概念块中不需要驻留到内存中的概念节点写回外存。对以上3个过程进行循环处理，直至处理完最后一个概念块为止，该算法结束。本文算法的伪代码描述如下：本文算法的伪代码描述如下：

算法：BlockLattice

输入：形式背景K以及对应的概念格L(K)，被减二元关系gIm

输出：新形式背景K*下的概念格L(K*)

Begin

list=getAffectedNodes(g,m，β);

inMemoryBlock=readBlock(list，α);

whilelist≠∅ do

judgeType(list,inMemoryBlock,α);

updateEdges(list,inMemoryBlock,α);

writeBlock(inMemoryBlock);

iflist≠∅ then

inMemoryBlock=readBlock(list,α);

End

BlockLattice算法的while循环实现了概念块的LRU调度顺序。函数getAffectedNodes()目的是遍历磁盘上的所有概念节点找出受影响节点，并将受影响的节点按外延所含对象数升序排列，即得到list受影响节点的索引表，按照此索引表划分概念块。函数伪代码描述如下：

函数：getAffectedNodes

输入：关系对象g以及关系属性m，每次读取概念节点数β

输出：list受影响节点的索引表

Begin

start:=0;

while start <= totalNums do

连接数据库，查询从start开始的β条记录；

for eachC∈ReultSet do

ifg∈Ext(C) andm∈Int(C)then

将C添加入list列表中；

概念节点按外延升序排列。

sart:=start+β;

End

totalNums变量保存概念节点总数。概念格存储在数据库中，数据库中的每条记录与概念节点一一对应，通过利用关系数据库的性能实现高效查询。getAffectedNodes()函数为了优化数据库查询效率，尽量合并多条记录进行统一查询，同时为防止结果集中数据过大，超出内存限制，将数据进行分页查询，β阈值即为分页大小。

本文算法中readBlock()函数是将list索引表中前α个受影响节点的概念簇读入inMemoryBlock内存等待处理。函数judgeType()判断当前块中受影响节点的具体类型，对节点进行相应的Ext(C)-{g} 或者Int(C)-{m} 处理，同时设置count域值。writeBlock(inMemory)函数是将count域为0的概念节点逐个写入外存文件，函数updateEdges()是对概念块中边进行更新处理并修改count域值。函数描述如下：

函数：updateEdges

输入：受影响节点列表list，驻留内存节点inMemory，概念块阈值α

输出：受影响节点列表list，驻留内存节点inMemory

Begin

count:=0;

whilelist≠∅ andcount<αdo

C=remove(0);

ifC.type:="ds" then //删除节点

读入Child(fBase(C))与Parent(cBase(C))；

isAddEdge(cBase(C),Parent(C));

isAddEdge(fBase(C),Child(C));

删除Child(C)与C以及Parent(C)与C的边；

从概念块中移除并销毁节点C；;

else ifC.type:="os" then //减对象节点

for eachCc∈Child(C) do

ifCc.type:="as"then

删除C与Cc之间的边；

isAddEdge(Cc,fBase(C));

isAddEdge(C,cBase(Cc));

upadateAsCount(Cc);

else ifCc.type:="ps"then

删除C与Cc之间的边；

isAddEdge(C,Cc.divided);

isAddEdge(Cc,fBase(C));

else ifC.type:="ps" then //分割节点

updatePS(C);

else //减属性节点，设置count域

ifC.count>0 then

for eachCp∈Parent(C)do

Cp.count=Cp.count+C.count;

cBase(C).count=cBase(C).count+C.count;

for eachCc∈Child(C) do

ifCc.type:="as"then

upadateAsCount(Cc);

End

updateEdges函数循环处理当前概念块中的受影响的节点，除减属性节点之外的其余受影响节点需遍历其所有子节点，若当前处理的节点与其子节点的边关系满足表2的情况。则该边需要删除。isAddEdge()用于判断两个节点间是否需要新增边，依据2.1节的定理这里不再赘述。upadateAsCount(Cc)表示如果节点Cc不是当前块中处理的减属性节点，则将Cc、Parent(Cc)以及cBase(C)的count域减1，表示这些节点已经被使用过一次。以下是对updatePS()的详细描述。

函数：updatePS

输入：受影响节点列表list，驻留内存节点inMemory，分割节点C

输出：受影响节点列表list，驻留内存节点inMemory

Begin

将C节点分割得到以下两个节点：

dividedC=(A-{g},B)与C=(A,B-{m})；

dividedC与C有相同子节点；

清空C的下界；

增加dividedCC父子关系；

C.dividedC=dividedC;

ifC.count>0 then //保留dividedC节点

dividedC.count=dividedC.count+C.count

for eachCc∈Child(dividedC) do

ifCc.type:="as"then

删除dividedC与Cc之间的边；

isAddEdge(C,cBase(Cc));

upadateAsCount(Cc);

ifCc.type:="ps"then

删除dividedC与Cc之间的边；

C与Cc新增边;

dividedC与Cc.dividedC新增边;

ifCc.count>0 and

Cc不是当前块处理的节点then

Cc.dividedC.count--;

End

函数updatePS是对分割节点进行处理，for循环是遍历分割节点的子节点，如果节点的类型为减属性或分割节点，则需要删除边关系，并判断是否新增边。

2.4 时间复杂度分析

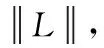
2.5 实例分析

借助本文算法可以辅助概念格完成具体的应用。当概念格较大而无法一次装入内存的情况时，利用本文算法的分块技术与调度策略，实现超内存概念格边维护边应用的过程。以下针对文献[12]的具体应用来说明BlockLattice算法的执行过程与实用价值。如表3所示给出一类场景下的BOV形式背景[12]，同时生成如图3所示的BOV概念格[12]。

文献[12]提出一种基于概念格层次分析的视觉词典生成方法，通过动态地调整外延数阈值β，获取各场景语义的约简视觉词典。当BOV形式背景生成的概念格规模较大

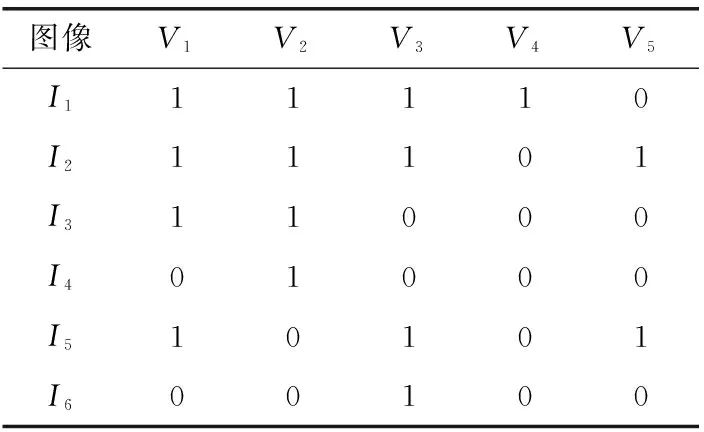
表3 BOV模型形式背景

图3 表3对应的BOV概念格

超出内存限制时，且形式背景中I1IV1二元关系消减的情况下，此时可以利用本文算法实现超内存BOV概念格的维护与应用。本文算法执行过程如下，外延数的阈值β[12]设置为2：

(1)遍历磁盘上所有概念节点，找到受影响节点列表：list={C0,C2,C4，C8,C7}， 同时计算外延数大于等于β的保留节点的内涵并集获得约简视觉单词为V1V2V3V5。

(2)逻辑上将概念格分块，设置概念块阈值α=2，则将概念格分成3个概念块，如图4所示。

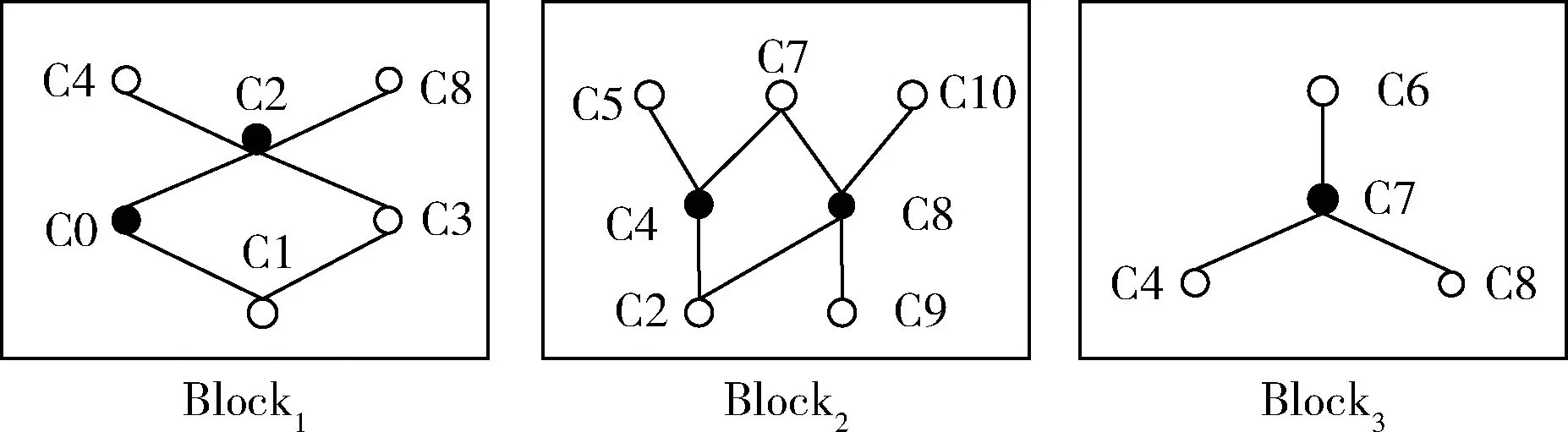
图4 概念格划分的3个概念块

(3)逐个处理概念块，同时计算每个块中受影响节点的约简视觉单词。根据就绪队列list列表，首先处理Block1块，将Block1读入内存并判断节点类型，同时计算约简视觉单词。根据文献[11]定义3可知，C0、C2是减属性节点，将C0,C2节点的内涵减去m属性，然后根据定理3可知以AS(K)为父节点的边不需要更新。处理完Block1得到约简视觉单词为V1V2V3V5。最后将Block1块写入磁盘，根据节点的外延与内涵可知，C4、C8均为受影响的节点，但不在该块中处理，故C2.count置为2，同样C3、C4、C8的count域也置为2。因此count域不为0的节点将驻留到内存中，其余节点写入外存。接下来依次处理Block2、Block3。最终每个块处理之后节点和边关系如图5所示。

图5 3个概念块处理后的状态

以上概念块中没有涉及到的边或节点，表示该边或节点从原始概念格至新概念格中保持不变，由2.1节的理论基础为依据。最终得到该场景下的视觉词典向量[12]为111010。同样利用以上的方法计算其它类场景下的视觉单词向量，并进行异或运算以消除多义词，从而实现图像场景的分类。详细过程参考文献[12]这里不再赘述。

通过以上实例分析可以看出本文的算法的分块技术和内外存调度算法可以很好的帮助概念格完成具体的应用，体现了本文算法的实用性。

3 实验结果与分析

本节使用Java语言编程实现本文所涉及的算法，程序运行在AMD Athlon(tm) 4core 3.4GHz CPU，4G内存，Win8OS的计算环境上，经测试JVM最大可用内存为1453 M。实验使用的是UCI公共数据集和随机产生的数据集。本文基于MySQL关系型数据库方式存储原始概念格，概念节点与数据库中的记录一一对应，利用关系数据库的性能来实现高效的查询与更新。

3.1 算法完备性验证

为了验证BlockLattice的生成概念格的完备性，在3个UCI公共数据集分别使用Godin算法[7]、AddIntent算法[8]和本文算法生成概念格，对比3种算法构造的概念格是否相同。对3个公共数据集CMSC[13]、ForestType[14]和BreastCancer[15]进行预处理得到形式背景，然后随机删除某个对象与属性之间的二元关系，Godin算法和AddIntent算法在新形式背景下够格，本文算法在原始概念格基础上调整得到新概念格。实验结果见表4。从表4中可以看出，本文算法与其余两种算法构造概念格所得概念节点数相同，并且概念节点之间的偏序关系也保持一致，从而验证了BlockLattice的正确性。

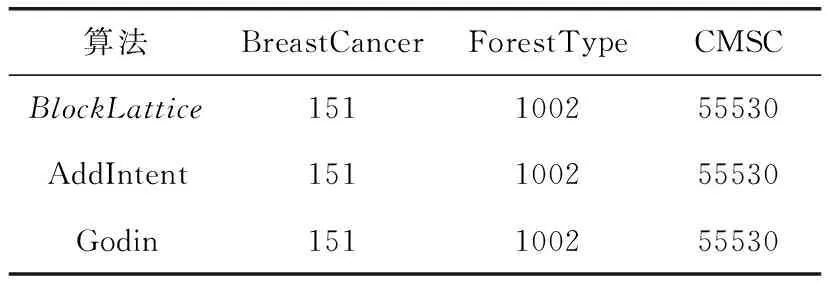
表4 3种算法产生的概念节点数

3.2 针对小规模数据集，算法时间效率对比

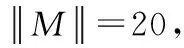
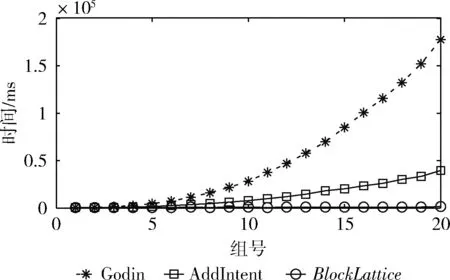
图时，3种算法时间效率对比

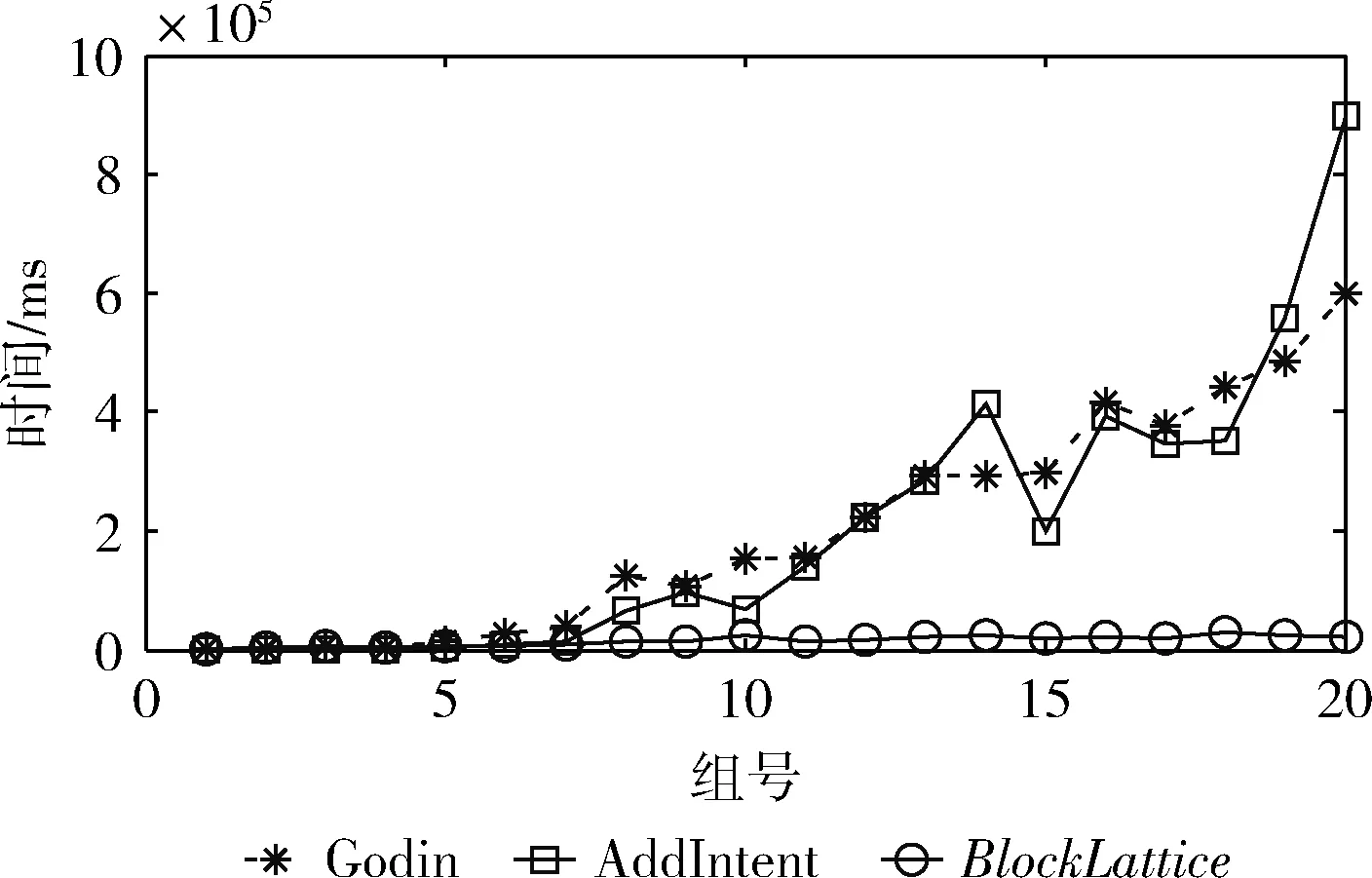
图时，3种算法时间效率对比

由图6、图7所示，相对于同样数量级的概念格，不管在稀疏还是稠密的数据集下，本文算法明显优于其它两类传统算法。这是由于本文算法不仅是在原始概念格的基础上调整得到新概念格，而且具有较低的时间复杂度，所以随着形式背景的规模不断增大，本文算法的执行效率相对于传统算法要好的多。

3.3 针对规模数据，BlockLattice算法效率分析

本节首先测试概念块α阈值对算法性能的影响，本组实验分别统计了I/O读写外存次数、内存计算时间Ti、外存操作时间To和总时间T，外存操作时间是指读写外存花费时间。本实验使用约2.83 GB的原始概念格，概念节点总数为1 422 225个，其中随机删除某个位置的二元关系使得受影响的节点数为988个。实验中概念块α阈值分别设置为1，10，100，1000。分页阈值β设置为105个，实验结果见表5、表6。

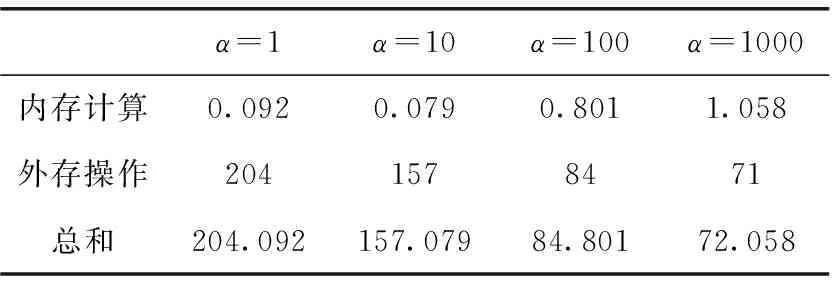
表5 当变化α阈值时的算法运行时间比较/s

表6 当变化α阈值时的I/O读写外存次数比较

由表5、表6所示，随着概念块α阈值的增加，To减少。具体地，因为α阈值的增加导致I/O读写次数减少。随着概念块α阈值的增加内存计算的时间曲线存在一个拐点(先降低后增加)，这是因为α阈值的增加使得存在父子关系的受影响节点尽量在同一块，减少了count域的维护，使得内存计算减少，但是对于内存中概念节点的查找时间随着内存中节点数的增加而增加，所以Ti随着α的进一步增加而增大。

然后测试分页β阈值对于算法性能的影响。本组实验分别统计了I/O读写外存次数、To、Ti以及T时间，α阈值设置为1000。实验结果见表7、表8。

由表7、表8所示，随着分页β阈值的增加，To减少，这是因为I/O读取次数减少。β阈值设置只作用于寻找磁盘上的受影响节点索引表的过程，它是为防止数据库的结果

表7 当变化β阈值时的算法运行时间比较/s

表8 当变化β阈值时的I/O读写外存次数比较

集过大出现内存溢出的情况而设置的并不影响内存的分块。在α相同且β不同的情况下，对于概念格中概念节点处理流程相同，因此内存计算的时间大致相同。

接着测试概念块α阈值对于内存中含有的最大概念节点数的影响。本组实验统计了程序运行过程中包含的最大概念节点数。实验结果见表9。

表9 当变化α阈值时驻留在内存中最大概念数比较(n=1422225)

由表9所示，随着概念块α阈值的增加，驻留在内存中的概念节点数也增加。当α阈值达到最大值1000时(概念格中受影响的节点数988)，驻留在内存中最大概念节点数只占总概念格节点数的2.43%，有效地降低了内存的消耗。

接着测试对于同一个规模数据，受影响节点总数对于算法性能的影响，由于删除不同位置的二元关系可得到不同的受影响节点总数。实验中概念块α阈值为1000，β阈值为105，删除3个位置的二元关系得到如表10所示的实验结果。

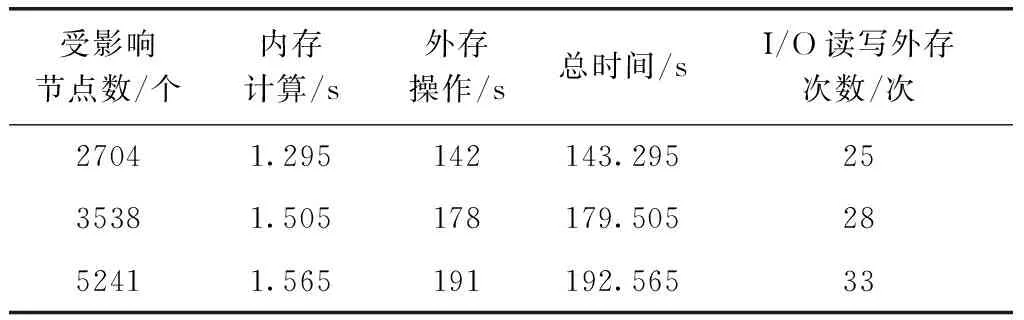
表10 受影响节点总数对算法性能的影响

由表10所示，针对同一个规模数据，在α与β相同的情况下，To、Ti和T时间以及I/O读写外存的次数随着受影响节点数的增加而增加。

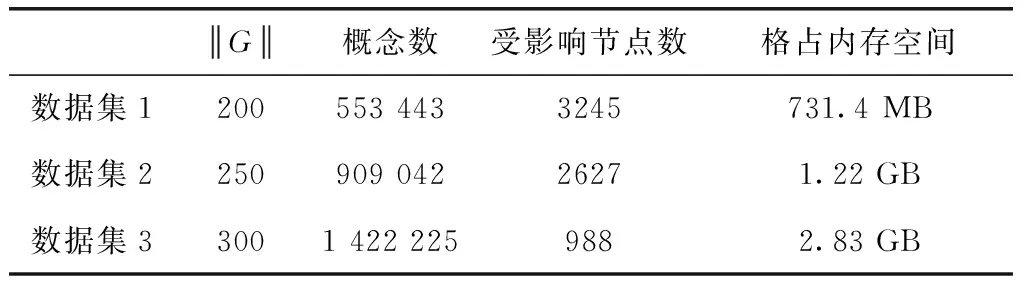
表11 3组随机数据集描述

实验中概念块α阈值设置为5、35、350、3500。限制内存空间为500 M，分页阈值β为105。实验分别统计了To、Ti以及T时间，实验结果如图8所示。横坐标表示概念块α阈值。

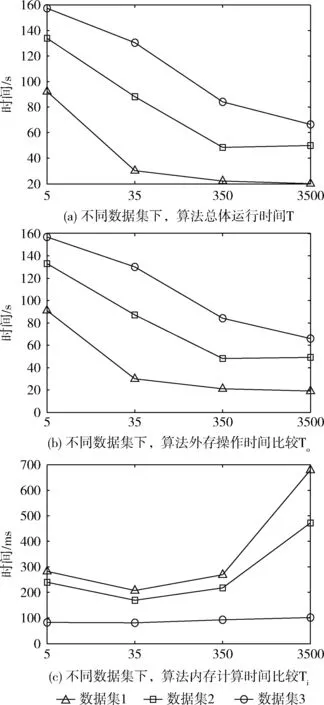
图8 不同数据集下，算法各项指标对比

由图8所示，在α、β阈值相等时，随着数据规模的增大，To、T时间增加，相反Ti减小。具体地，因为数据量增大导致I/O读写外存次数增加致使To、T时间增加；又因为Ti主要与受影响节点总数以及α阈值有关，当α相同时，Ti随着受影响节点总数的减少而减少。

通过以上多组实验得到以下结论：①影响算法性能的主要因素为外存操作时间，即I/O读写外存的次数。数据规模、受影响节点总数以及α与β阈值都会影响I/O读写外存的次数，表现为I/O读写外存的次数随着α与β阈值的增加而减少，随着数据规模、受影响节点总数的增加而增加。②算法消耗内存的情况主要取决于数据规模、受影响节点总数、α以及β阈值。α与β阈值的增加使得消耗的内存也增加，但由于受影响节点总数是有限的，当α阈值增加到一定程度时，驻留在内存中的最大概念数存在最大值，内存消耗不会无限制增加，且通过调节α阈值可以明显降低内存的消耗。因此依据当前平台参数、概念格的规模以及受影响节点总数，合理调整α与β阈值，使得BlockLattice算法执行效率达到最优。

4 结束语

本文对超内存概念格维护问题进行了研究，和以往的传统的基于内存的维护算法相比，本文研究的问题还需要考率如何充分利用内存资源，减少I/O读写次数。为了解决上述问题，本文以形式背景中对象与属性之间二元关系消减为应用背景，提出一种有限内存空间下超内存概念格内外存调度维护算法。本文首先将二元关系消减理论进一步改进优化以提高数据处理能力。然后利用基于概念簇的方式划分概念格使得分块质量变高(块内高内聚，块间低耦合)，为契合概念格在实际应用中遍历概念格的方式，采用自底向上最近最少使用的调度策略处理概念块，最后通过实例验证本文算法在概念格实际应用中的实用价值。本文从理论分析与实验结果两方面表明本文算法与传统算法相比，不仅节约了大量的运行时间，而且也降低了内存的消耗，解决了内存不足的现象，实现了超内存概念格的维护，为概念格的具体应用提供保障。

[1]Yang Kai,Jin Yonglong.Research of coke ratio prediction based on concept lattice and genetic algorithm[C]//Mechatronics and Automation.IEEE,2016:1407-1411.

[2]Roman Ilin.Classification with concept lattice and choquet integral[C]//Information Fusion.IEEE,2016:1554-1561.

[3]Shi Chongyang,Lai Linjing,Fan Jing,et al.Similarity model based on CBR and FCA[C]//Software Engineering,Arti-ficial Intelligence,Networking and Parallel/Distributed Computing.IEEE,2016:597-603.

[4]Goidn R.Incremental concept formation algorithm based on Galois (concept) lattices[J].Computation Intelligence,1995,11(2):246.

[5]Merwe D V D,Obiedkov S,Kourie D.AddIntent:A new incremental algorithm for constructing concept lattice[G].LNCS 2961:Proc of the 2nd Int Conf on Formal Concept Analysis.Berlin:Springer,2004:372.

[6]MA Yuan,MA Wensheng.Construction of multi-attributes decrement for concept lattice[J].Journal of Software,2015,16 (12):3162-3173(in Chinese).[马垣,马文胜.概念格多属性渐减式构造[J].软件学报,2015,16(12):3162-3173.]

[7]JIANG Qin,ZHANG Zhuo,WANG Liming.Algorithms of constructing concept lattice based on deleting multiple attributes synchronously[J].Journal of Chinese Computer Systems,2016,37(4):646-652(in Chinese).[姜琴,张卓,王黎明.基于多属性同步消减的概念格构造算法[J].小型微型计算机系统,2016,37(4):646-652.]

[8]Zhang Zhifeng,Zhang Na.A LOD algorithm based on out-of-core for large scale terrain rendering[C]//Mechatronic Sciences,Electric Engineering and Computer.IEEE,2013:2168-2171.

[9]GU Runnan,AI Zhongliang.Massive data processing algorithm based on LOD control and out-of-core techniques[J].Computer Engineering & Software,2016,37(3):89-93(in Chinese).[古润南,艾中良.基于LOD控制与内外存调度的大规模网络态势数据节点处理算法[J].软件,2016,37(3):89-93.]

[10]Baralis E,Cerquitelli T,Chiusano,et al.Scalable out-of-core itemset mining[J].Information Sciences,2015,293(1):146-162.

[11]WANG Chunyue,WANG Liming,ZHANG Zhuo.Algorithm of maintaining concept lattice based on binary relation decrement[J].Computer Science,2016,43(14A):34-41(in Chinese).[王春月,王黎明,张卓.基于二元关系消减的概念格维护算法[J].计算机科学,2016,43(14A):34-41.]

[12]ZHONG Lihua,ZHANG Sulan,HU Lihua,et al.A concept lattice hierarchy based generating method of visual dictionary[J].Journal of Computer-Aided Design & Computer Graphics,2015,27(1):136-141(in Chinese).[钟利华,张素兰,胡立华,等.基于概念格层次分析的视觉词典生成方法[J].计算机辅助设计与图形学学报,2015,27(1):136-141.]

[13]Lucas DD,Klein R,Tannahill J,et al.Climate model simulation crashes dataset[EB/OL].[2016-12-18].http://archive.ics.uci.edu/ml/datasets/Climate+Model+Simulation+Crashes#.

[14]Brian Johnson.Forest type mapping data set[EB/OL].[2016-12-18].http://archive.ics.uci.edu/ml/datasets/Fo-rest+type+mapping.

[15]William H.Breast cancer wisconsin (diagnostic) data set[EB/OL].[2016-12-18].http://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Diagnostic%29.