可证明安全的可擦除脆弱数字水印
2018-03-19童伟,朱岩
童 伟,朱 岩
(1.青海大学 计算机技术与应用系,青海 西宁 810016;2.北京科技大学 计算机与通信工程学院,北京 100083)
0 引 言
数字媒体的无损表示、存储和应用对数字媒体的保护提出了更高的要求。传统的数字媒体保护采用了数字水印技术来宣称作品所有权、来源认证以及完整性验证,也就是通过利用媒体所具有的冗余性在数字媒体中嵌入指定的信息来达到各种安全目标。然而,这种嵌入水印的方式会对数字媒体带来失真,这有违于我们对数字媒体的无损处理的需要。
为了解决这一问题,一种称为脆弱水印的特殊数字水印技术被提出。脆弱水印[1]是一种可实现精确认证或原数据认证的水印技术,它能保证任何原作品中任意一比特的变化都被检测出来。然而在作品中嵌入水印也会修改作品,这就增加了辨别作品篡改和水印修改的困难。为了解决这一问题,脆弱水印中可以采用可擦除水印技术,也就是以一种可完全去除或擦除的方式嵌入信息[2],且能在认证的过程中逐个比特地恢复出作品的原貌,同时保留脆弱水印的精确认证功能。
这种数字媒体认证技术被[3]称为“可擦除脆弱水印”技术。鉴于这种技术的优点,本文提出了一种可擦除脆弱水印构造方案,并对该方案的检测性质和安全性质进行了形式化证明,包括:错误检测的最大似然估计、签名信息不可预测性(签名隐藏的语义安全)、抗篡改攻击性(签名不可伪造性)[4],这表明所述方案是一种具有密码学安全的数字媒体认证技术。
1 脆弱水印的定义
给定数字作品X,一个数字媒体认证系统被称为脆弱水印方案,如果下面条件满足:
(1)密钥生成:根据安全强度κ随机选择密钥k,即WGenKey(1κ)→k;
(2)伪文构造:在作品中嵌入消息摘要,并生成带摘要的伪文作品,即,WSignk(X)→X′;
(3)完整性认证:完成作品是否修改的验证,并恢复原作品,即
WVerifyk(X′)→(X″,true/false)
脆弱水印满足数据认证的完整性要求[5],也就是,对于有效生成的带水印作品,将以概率1通过完整性验证
作为一个完整性检验方案[6],脆弱水印需要满足不可伪造性,也就是,对于任何没有密钥的敌手,给定原始作品X,不能伪造一个能通过完整性认证的作品X*。此外,脆弱水印需要满足不可篡改性,也就是,对于任何没有密钥的敌手,给定一个带有水印的作品X′,不能伪造一个能通过完整性认证的新作品X*且X≠X*。
2 脆弱水印构造
基于上述思想,使用可擦除水印系统S和一个带密钥的MAC函数,我们给出一种脆弱水印实现方案,并证明该方案具有和密码学上的完整性验证方法相同的安全性,该方案函数定义和基本设计框架如下:
(1)密钥生成:随机选择适合MAC和可擦除水印的密钥k;
(2)伪文构造:在作品中嵌入消息摘要,过程如下:
1)计算摘要:通过调用σ←MACk(X)实现;
2)嵌入水印:通过调用X′←Embedk(X,σ)实现;
(3)完整性认证:完成作品是否修改的验证,过程如下:
1)抽取摘要:通过调用σ′←Extractk(X′)实现;
2)擦除水印:通过调用X″←Erasek(X′,σ′)实现;
3)完整性认证:如果MACk(X″)=σ′,返回true;否则,返回false。
上述脆弱水印构造流程如图1所示,通过密码学方法和数字水印技术的结合,可实现可证明安全的脆弱水印方案。
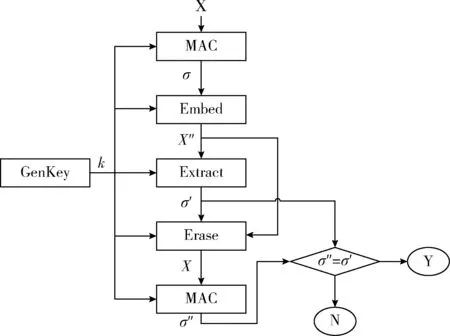
图1 脆弱水印的通常构造
下面我们将采用密码学MAC函数和扩频水印给出一种具体的脆弱水印方案:
(1)密钥生成:由签名者生成随机密钥k,并与验证者共享该密钥。
(2)伪文构造:这一算法产生验证信息并嵌入数字媒体,处理如下:
1)作品的创作者用作品全部信息计算出签名。可采用某个消息认证码MAC算法获取原图像X的L比特的认证码
σ←MACk(X)
2)将签名用一种可擦除的方式嵌入作品。将认证码σ表示为二进制形式,并通过映射转换为矢量σ={σ1,σ2…,σL}∈{-1,1}L,其中,σi∈{-1,1}。按照嵌入信息数量将原始图像转换为等长度N的L块X={X1,X2,…,XL},每块Xi={xi1,xi2,…,xiN}嵌入一位信息。
3)根据密钥k,使用伪随机数生成器构造L个伪随机序列wi={wi1,wi2,…,wiN}且对于所有i∈[1,L],j∈[1,N],wi,j∈{-1,1}。采用扩频水印嵌入方法,将认证码逐比特σi嵌入图像中第i块中第k像素xik中,具体嵌入公式如下:对任何i∈[1,L],k∈[1,N]
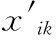
(1)
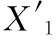
(3)完整性认证:验证者给定密钥k可按以下步骤检测图像完整性:
1)接受者提取嵌入的信息。按照扩频水印的提取方法,首先,由密钥恢复出L个伪随机序列wi={wi1,wi2,…,wiN}∈{-1,1}N,对于所有i∈[1,L];其次,通过计算图像序列与该随机序列相关值
其中,Xi*wi表示两个向量的数量积。最后,由相关值提取嵌入信息
这里,要求嵌入的信息与提起的信息σ′={σ1,…,σL}必须是一致的。
2)接受者从载体作品中擦除水印。这一过程是嵌入过程的逆过程:对任何i∈[1,L],k∈[1,N]
(2)
不难发现,只要提取信息和随机序列是一致的,那么擦除水印的作品和原作品是完全一致。
3)为了验证是否一致,验证者对作品求取MAC,即,σ″←MACk(X″),并将σ″与解码获得的签名σ′进行比较,当且仅有以上两个哈希签名一致(σ′=σ″),接受到的作品才能通过认证。
3 性能与安全性分析

证明:对于每一嵌入比特σi∈{0,1}的检测,可以看作在两种假设H1和H-1中的参数检测问题,其中,H1表示存在信息σi=1,H-1表示存在比特信息σi=-1,因此,水印检测过程可表示为如下的二元假设检验

下面采用多样本二元假设的最大似然比对上述分布进行估计校验
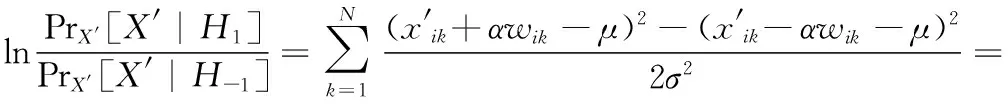
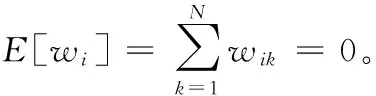
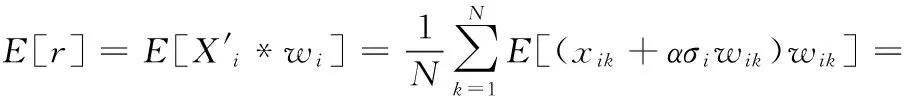

下面分析算法安全性。即使攻击者能够获得原作品,只要密钥是未知的,那么上述脆弱水印方案具有签名的不可猜测性:
定理2 签名信息不可预测性:给定原作品(掩文)X和带水印作品(伪文)X′,敌手无法猜测签名信息σ的成功概率为1/2L。

由于wik是由伪随机数发生器产生的,因此它的取值概率有Pr[wik=1]=Pr[wik=-1]=1/2。
因而,我们可知

同样地,我们可以证明Pr[σiwik=-1]=1/2。因此,即便图像签名σ不是均匀分布的,敌手所观察到的水印序列{σiwik}是均匀分布的,因而,对于一个L长的图像签名σ,敌手猜测成功的概率依然是1/2L,定理得证。
数字作品的签名计算需要密钥k,因此对于任何没有密钥的敌手,给定一个带有水印的作品X′,篡改作品首先需要获取其中隐藏的签名σ。但上述定理即使能够获取原作品X,也无法得到其中的签名σ,这对篡改是非常不利的。下面将进一步证明脆弱水印的防篡改功能。
定理3 抗篡改攻击性[8]:脆弱水印方案能够检测对作品的篡改。
证明:假设敌手在未知密钥情况下对带水印的作品X′进行了修改,获得一个新的版本X*,且X′≠X*,但X*能够通过完整性验证。验证者采用密钥k提取到签名σ*←Extractk(X*),则存在两种情况:

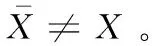



基于上述讨论,证明的前提假设不成立,那么任何对带脆弱水印作品的篡改都可被检测,问题得证。
上述证明中敌手即使能够攻破强碰撞性质,那么依然不可能伪造有效的作品,原因在于:根据定理2,敌手即便观察到了非常大量的相同密钥k的带水印作品,仍然不能准确的获得其中的σ信息,这是与MAC强碰撞假设不一致的,显然这将增加敌手攻击的难度。
4 实例分析
下面以一个实例来说明脆弱水印的构造和完整性认证[10]过程:
(1)选取一个80 bits的整数作为密钥k=355778428493926306668578;
(2)采用SHA256作为Hash函数,采用HMAC生成256 bits消息

(3)选取“狒狒”图片作为掩文,大小为256×256像素,如图2左图所示,在右图中我们给出了它的直方图。
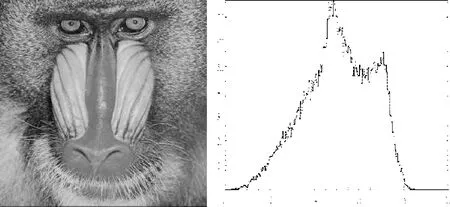
图2 载体图像(256*256)及其直方图
(4)为了将前述256 bits信息隐藏其中,可令每行像素存储1 bit信息。例如,对于第10行,需要隐藏的信息比特为-1,所采用的扩频N(0,1)序列为
对第10行图像中的像素,我们有下面向量
进而,根据嵌入公式,令α=10,我们可以得到下面嵌入信息后的像素向量
经过上述处理,可得到载有水印的图像,如图3左图所示,同时,在右图也显示了该图像的直方图,可以看出,图像中有个别点出现了亮点,这是由于模运算截断多导致的,直方图有所变化。
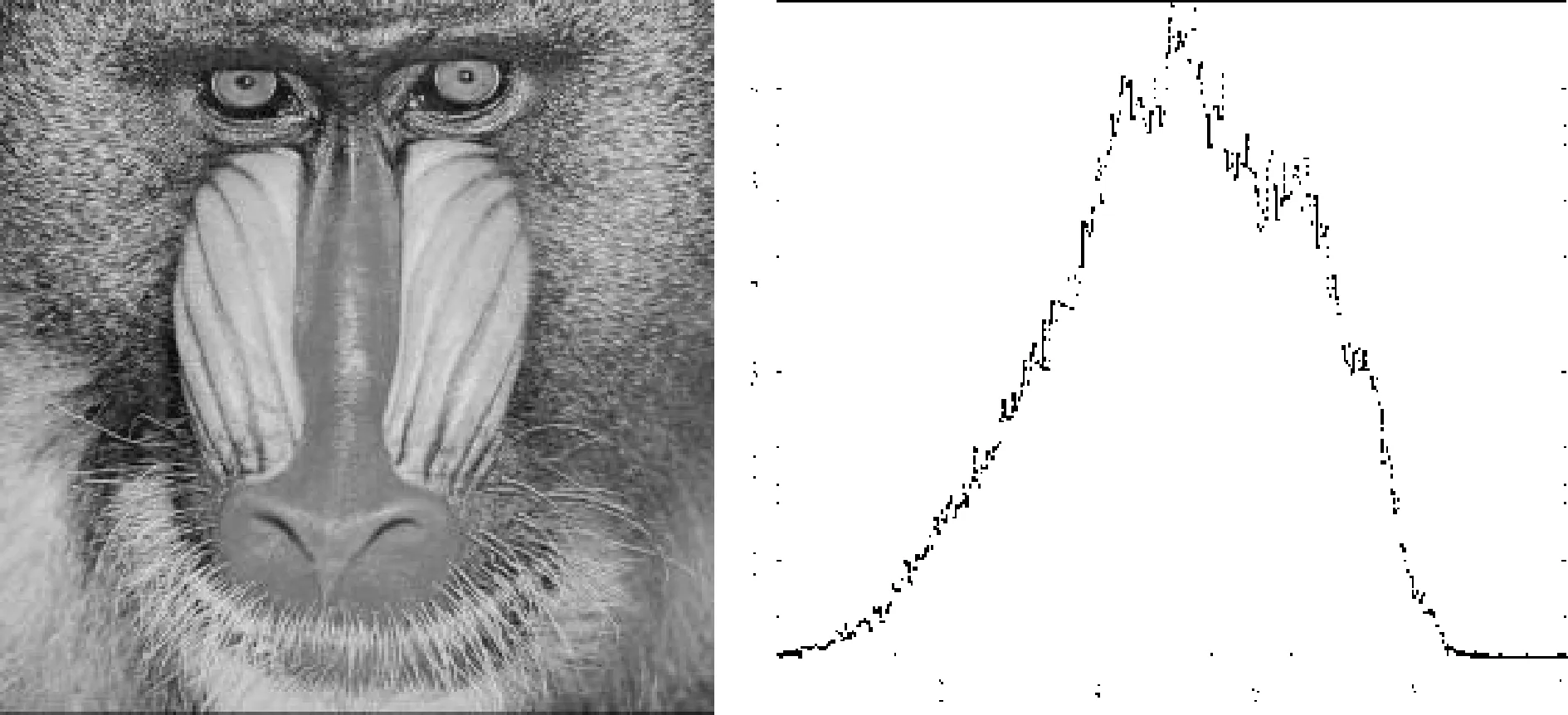
图3 载有水印后作品
(5)下面演示检测过程。首先,通过相关方法提取出隐藏的MAC信息,例如,对于上述第10行,计算相关值

图4 相关检测值的分布以及擦除水印后作品
最后,我们对图像进行还原,如图4右图所示,可以看出原图被很好地再现,也就是X″=X。进而,我们测试σ′=MACk(X″)成立,这表明图像没有任何改动。
5 结束语
脆弱水印技术通过密码学的哈希函数对其的安全性进行合理的保证。鉴于目前已有研究成果在很多方面并不是十分完善,本文提出了一种可擦除脆弱水印构造方案。该方案不仅可以证明具有错误检测的最大似然估计、签名信息不可预测性、抗篡改攻击性,使得该方案在认证的过程中能够逐个比特地恢复出作品的原貌,并且还可以控制不丢失脆弱水印的精确认证功能。上述工作表明,构造一种具有密码学安全的数字媒体认证技术是完全可行的。
[1]HUANG Huajun,JIANG Liqing,XIE Lili,et al.Based on semi-fragile watermarking phishing active defense technology[J].Information Network Security,2013(1):8-11(in Chinese).[黄华军,姜丽清,谢黎黎,等.基于半脆弱水印的网络钓鱼主动防御技术[J].信息网络安全,2013(1):8-11.]
[2]CAI Jian,WANG Shumei.A hadamard transform and chaos theory based fragile watermarking algorithm[J].Modern Computers(Professional Edition),2014(2):23-27(in Chinese).[蔡键,王树梅.一种基于哈达玛变换与混沌理论的脆弱水印算法[J].现代计算机(专业版),2014(2):23-27.]
[3]LU Wei.Multimedia copyright protection based on digital watermarking and digital signature protocol research[C]//The Cryptography and Information Security Teaching Conference in 2010,2012(in Chinese).[卢炜.基于数字水印与数字签名的多媒体版权保护协议研究[C]//2010年全国密码学与信息安全教学研讨会,2012.]
[4]YE Chuang.Digital watermarking algorithm based on discrete wavelet transform research[D].Hangzhou:Zhejiang University,2012(in Chinese).[叶闯.基于离散小波变换的数字水印算法研究[D].杭州:浙江大学,2012.]
[5]ZHI Ce,MA Zhaofeng,JIANG Ming,et al.Based on the PDF integrity authentication of digital watermarking research[J].Journal of Information Security and Communications Confidential,2012(10):63-66(in Chinese).[支策,马兆丰,蒋铭,等.基于数字水印的PDF完整性认证研究[J].信息安全与通信保密,2012(10):63-66.]
[6]Kashyap N,Sinha GR.Image watermarking using 3-level discrete wavelet transform(DWT)[J].International Journal of Modern Education & Computer Science,2012,4(3).
[7]LI Guo’an,HUANG Lintao,LI Jianfeng.Maximum likelihood estimation method of the exploratory teaching[J].Journal of University Mathematics,2013,29(3):144-146(in Chinese).[李国安,黄林涛,李建峰.最大似然估计法的探究式教学[J].大学数学,2013,29(3):144-146.]
[8]JIN Xizi,JIANG Wenzhe.Block-level tamper with the positioning of the JPEG image fragile watermarking[J].Journal of Electronic,2010(7):1585-1589(in Chinese).[金喜子,姜文哲.块级篡改定位的JPEG图像脆弱水印[J].电子学报,2010(7):1585-1589.]
[9]ZHOU Qinglei,LI Bin.Double software watermark scheme based on tamper-proof[J].Computer Engineering,2013,39(7):185-188(in Chinese).[周清雷,李斌.基于防篡改的双重软件水印方案[J].计算机工程,2013,39(7):185-188.]
[10]Su Q,Niu Y,Wang G,et al.Color image blind watermar-king scheme based on QR decomposition[J].Signal Proces-sing,2014,94(1):219-235.
