基于虚拟力和泰森多边形的分布式覆盖算法

祁春阳，戴 欢，赵晓燕，李克清,4+

(1.中国矿业大学 计算机科学与技术学院，江苏 徐州 221116；2.苏州科技大学 电子与信息工程学院，江苏 苏州 215009；3.常熟理工学院 计算机科学与工程学院，江苏 常熟 215500；4.苏州市职业大学 计算机科学与工程学院，江苏 苏州 215002)

0 引 言

近些年来，学术界提出了不少无线传感器网络[1]覆盖算法。通常将这些算法归结为两类：一方面是集中式覆盖算法，即通过预先部署固定节点在限定区域内，通过节点通信范围计算此限定区域的覆盖率，而后加入移动型节点，由集中式算法获得的网络全局信息对于覆盖盲区进行补充、修整。代表算法有粒子群优化算法[2](particle swarm optimization，PSO)、概率感知模型算法[3]等。另一方面是分布式覆盖算法，即直接部署移动节点，通过感知周围节点的信息进行自主移动提高覆盖率，无需获取全局网络信息，减少能量消耗，具有部署简单、自主化程度高等特点。代表算法有虚拟力算法[4](virtual force，VF)、节点感知方向调节算法[5](distributed node orientation adjust，DNOA)。

虚拟力算法的主要思想是在限定区域内寻找节点间的受力平衡位置，以此作为传感器节点在后期相关算法迭代过程中的移动位置。基于虚拟力的覆盖算法，取得了较好的覆盖率，但其计算量大、收敛速度慢并且易陷入局部最优，使其覆盖率出现不稳定现象。本文提出了基于虚拟力和泰森多边形划分[6]的分布式覆盖算法，该算法可有效避免单独虚拟力情况下陷入局部最优，实现较高覆盖率。

1 算法的提出

1.1 虚拟力算法

虚拟力算法由物理学中力的相互作用引入覆盖问题的研究[7]，此算法假设所研究的限定区域内的节点间存在相互力，在无线传感器节点覆盖算法优化中采取节点所受合力移动方式，直到区域节点间相互受力平衡。假设无线网络中的传感器节点si的所受虚拟力为Fi；传感器节点sj对传感器节点si的力为Fij，相邻传感器节点间距离为d。FiR定义为限定区域内未被覆盖的网格节点对传感器节点si的合力，若区域边界存在大量节点，根据上述规则必然会存到强斥力作用，将会浪费一些传感器节点的覆盖能力，此时规定一个边界约束力Fb，传感器节点所受合力如式(1)所示

(1)

其中，传感器节点间的相互作用力Fij包含引力和斥力两个部分，当区域内的特定范围节点密集时斥力影响大于引力，反之同理。根据最终引力和斥力的大小确定移动距离和位置，各传感器根据虚拟力将原位置(xold,yold)更新为新位置(xnew,ynew)，如式(2)所示

(2)

其中，MS为传感器节点在算法单次迭代过程中的最大移动距离，Fxy是全局对传感器节点的合力，Fx，Fy是传感器节点所受合力两个二维分量，分别表示为传感器节点在x轴和y轴所受力的分量。虚拟力方案可有效的扩散限定区域内节点，使其处于一种相对平衡的位置。

1.2 Voronoi图

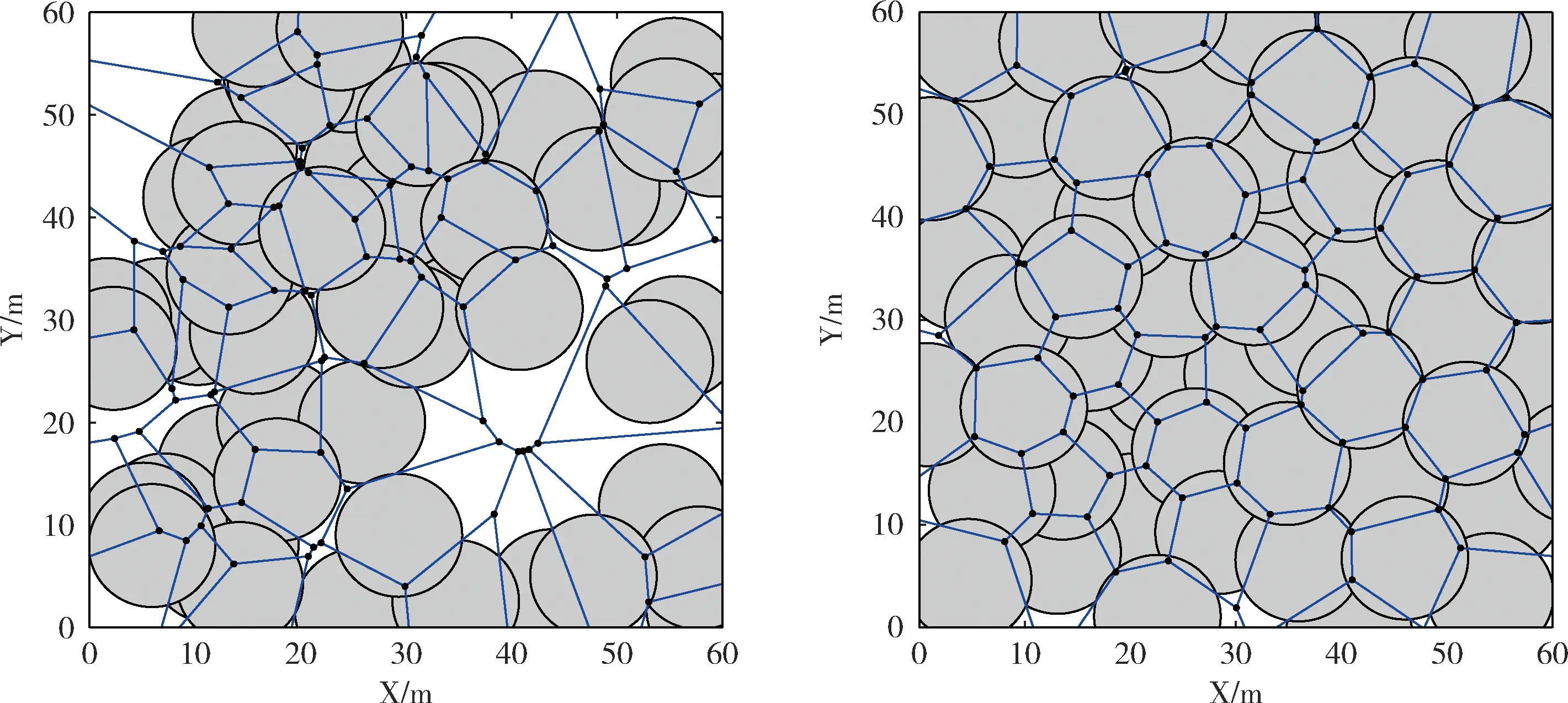
Voronoi图是基于Delaunay三角对于空间内限定区域采用节点中垂线相连接方法组成的区域划分图，采用欧式距离为标准对于平面区域进行分块[8]。由于Voronoi图具有最近性、邻接性等性质和比较完善的理论体系，所以Voronoi图常被用来解决影响范围、最近邻近查询问题、最大空圆问题和Delaunay三角对偶问题[9]。构建Voronoi图的基本思想：基于限定平面区域内的随机离散节点集(如图1所示)中的相邻节点做出中垂线，然后去除多条中垂线连接后的多余线段，形成多块不同形状的多边形，并且每个多边形中包含唯一对应的节点，最终形成一个对于该节点的最近二维平面区域，形成的二维区域内的所有数据点集距离区域内该点的距离相对于距离邻近区域的点都为最近。即对应该节点的影响范围称为Voronoi多边形(如图2所示)，若删除任意生成点，那么与之对应的影响范围将消失，并且只能影响与之邻近的Voronoi多边形区域。

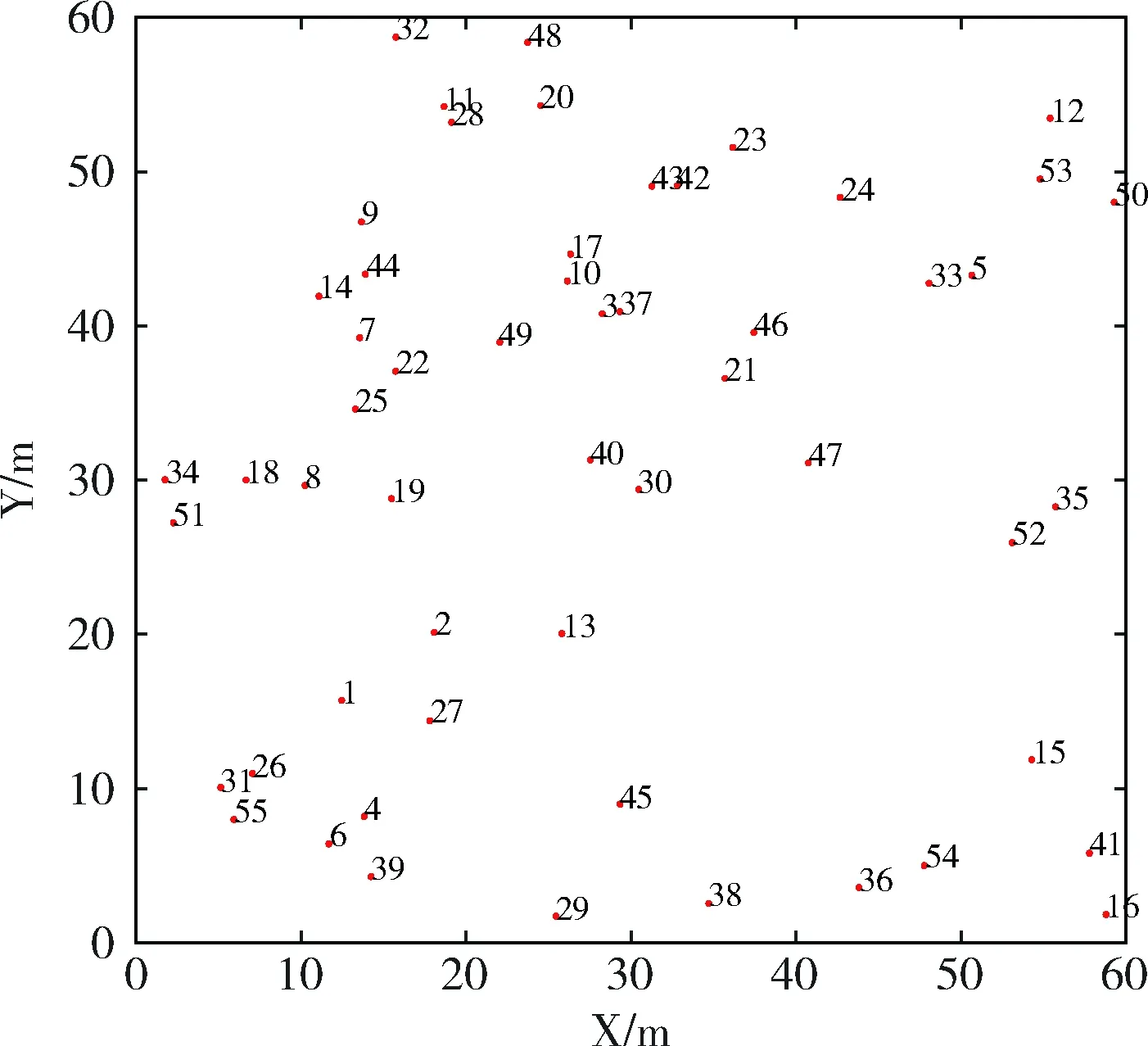
图1 随机部署节点初始位置

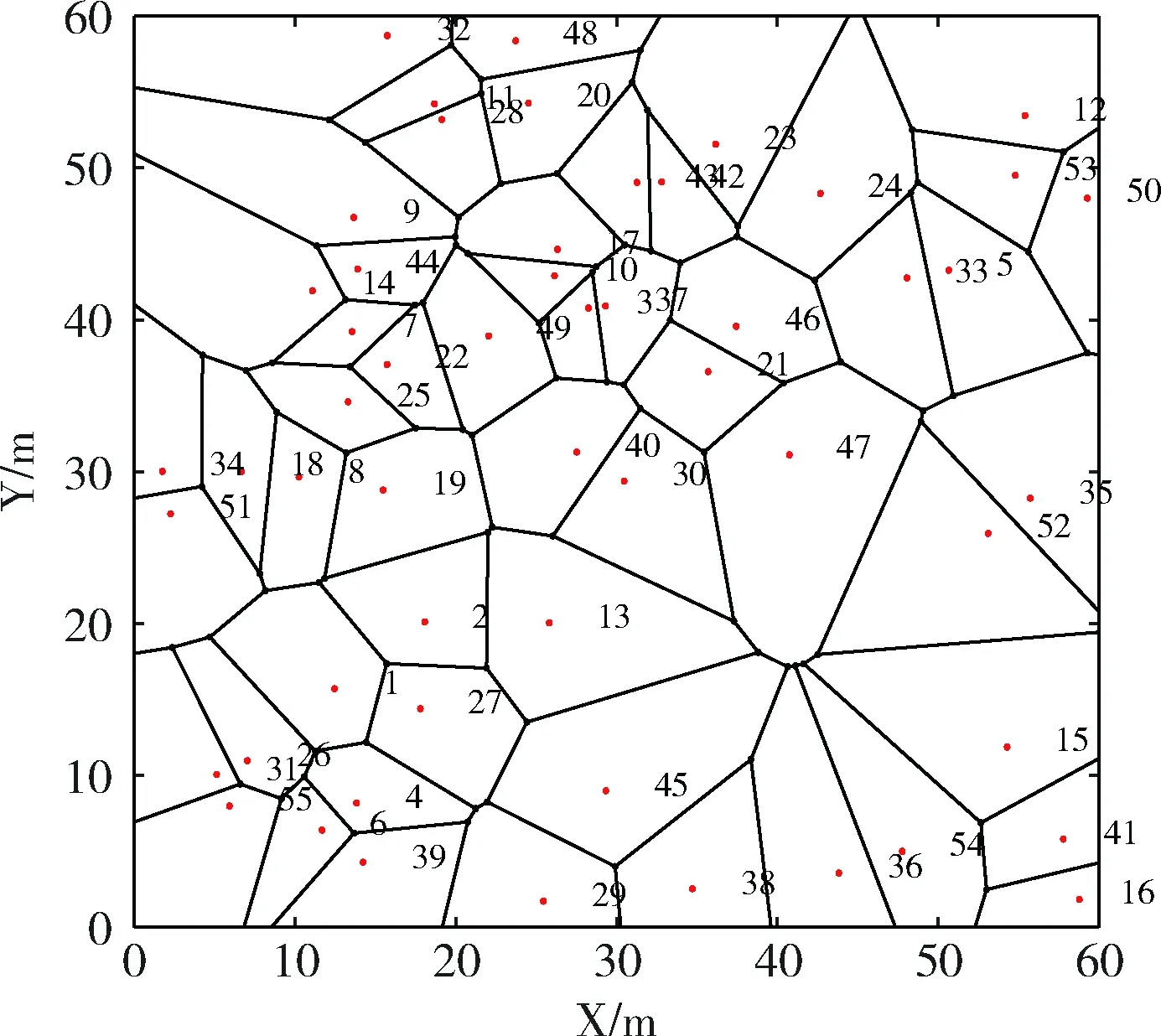
图2 Voronoi划分下的初始节点位置

基于以上的Voronoi几何方案，引入质心算法、Minmax算法将提高虚拟力条件下的后期覆盖率稳定性及收敛速度，可在较少的迭代次数下获得较好的网络覆盖率。

2 VFVP覆盖算法

上述虚拟力算法可以相对解决前期传感器节点分布过于密集的问题，Voronoi算法具有很强的区域划分能力，有利于提升算法的收敛速度，质心算法可以优化节点迭代过程中的移动位置[10]，因此本文提出了一种VFVP算法策略，算法流程如图3所示。

图3 算法流程

2.1 网络模型构建

假设有N个节点，每个节点感知半径为Rs。无线传感器网络节点集S被随机部署在一个二维空间A内[11]，节点具有自主移动性，其通信半径为Rc，Rc≥2Rs。节点Si属于S集合，以节点为感知圆心，假设节点具有以下性质：①初步在监测区域部署移动传感器节点，其拒用可移动性，可根据自身优化的分布式算法进行自主移动到相对位置，节点间相互采取分布式通信逐个建立无线传感器网络；②节点的通信半径为感知半径的2倍，即Rc=2Rs,任意两个节点互为邻居；③将监测区域进行分割成正方形，计算在传感器节点感知半径内的格点数，计算覆盖率。

2.2 相关定义

定义1 节点集：监测区域A内随机部署节点集S，将A根据节点集S划分为不同的Voronoi多边形区域，即Si∈Vi(S，Rs，V), 其中，Vi为Si所在Voronoi多边形区域。传感器节点集S⊂V。

定义2 衍生节点集：已知监测区域A被划分为多个不规则的Voronoi多边形，因多边形区域根据随机部署的节点集划分，每个不规则多边形内包含一个可移动传感器节点S1，多边形的各个顶点集为衍生节点集W，记对应节点S1的衍生节点集个数为k。

定义3 质心节点集：定义2中给出了衍生节点集W，将衍生节点集进行质心计算得到质心节点集N，如式(3)、式(4)所示

(3)

(4)

2.3 离散节点覆盖率计算

假设二维空间A，被划分为m×n个网格节点，网格节点Q的坐标为(xi,yi)，其中，节点Si={xi,yi,RS}， 则Q点与节点Si的距离为d(Si,Q)。由布尔模型得出节点Si与网格节点Q的概率模型

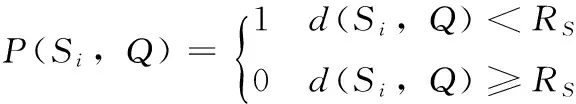
(5)

由于实际环境中的噪声等其它因素的干扰，节点测量模型表现出特定的概率分布

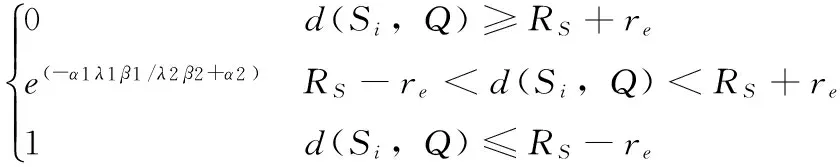
(6)

式(6)中的re(0

由以上公式所得，对于点的监测概率有可能是小于1，因此通常使用传感器节点多点联动方案，其概率分布如下

(7)

在网格划分中，网格节点Q被传感器节点有效覆盖的标准如下

P(S,Q)≥cth

(8)

式(8)的cth表示网格节点是否被有效覆盖的阈值。

区域覆盖中的覆盖率表示为传感器节点的感知范围与监测区域A面积的比值，将A离散分割后，覆盖率表示如下

(9)

式(9)中参数count由式(8)给出有效覆盖网格节点数。

2.4 算法步骤

本文算法可分为以下4个阶段：

步骤1 由虚拟力算法将节点集S充分受力尽可能分布均匀；

步骤2 关闭虚拟力，为移动后节点集S进行Voronoi划分，对检测区域A内的衍生节点集W进行存储；

步骤3 将区域A内的点集W进行质心改进，得到质心点集N；

步骤4 将质心点集与移动后节点集进行对比移动，优化位置；

步骤5 Minmax算法调整后期精度，提高节点覆盖在迭代后期稳定性。

3 实验仿真及结果分析

3.1 实验仿真

为了验证VFVP分布式覆盖优化策略的覆盖程度与收敛速度，与VF、VFVM、VFC覆盖优化策略做了对比实验。仿真环境：Matlab 2015。实验过程中分析了无线传感器节点对监测区域的覆盖程度及收敛速度，两项指标定义如下：①覆盖程度：所有节点的覆盖面积总和与整个监测区域的比值。②收敛速度：对比虚拟力算法在同一时间节点下的覆盖率。

假设在边长60 m的正方形区域内布置55个可移动的无线传感器节点，所有传感器节点的测量半径为6 m，节点通信半径Rc=2Rs。图4显示节点的初始随机分配状态和算法最终覆盖图，该状态下的节点在覆盖区域的左上角和中间部分形成了大量的覆盖重合节点，使得监测区域内的覆盖率很低，经过VFVP算法规划后得到很好的覆盖效果。VF算法代表虚拟力下的覆盖算法，VFVM算法为虚拟力环境下加入Voronoi规划、Minmax的覆盖算法，VFC代表虚拟力条件下直接使用质心算法的覆盖模式。图5给出了4种算法运行过程中覆盖情况，可看出算法在迭代了25次的情况，覆盖率得到明显提高，对比3种算法迭代相同次数的结果。VFVP算法在初期运行方面得到的覆盖率明显高于VF、VFVM、VFC算法。

图4 VFVP初始状态和算法结果

图5 迭代次数为25次时节点覆盖情况

3.2 覆盖率与收敛速度评估

无线传感器网络中节点对于监测区域的覆盖率与收敛速度是判断算法优劣的重要指标，如图6所示。

图6 迭代过程覆盖率增长

引入Voronoi规划的VFVP算法在监测区域A中的覆盖率都优于另外3种算法，该算法随着迭代次数的增加，覆盖率上升较为平滑。虚拟力算法前期收敛速度较慢，VFC算法初期快速收敛现象很好解决了这个问题。但VFC算法后期出现覆盖率的大幅度降低，VFVP算法的出现解决了后期VF算法覆盖率不规则下降的问题，通过Minmax算法的后期调整得到了很好的效果。

如图7所示，虚拟力算法存在着收敛速度慢，引入质心解决方案后的VFVP算法收敛速度得到了很大的提升，质心解决方案中采取Voronoi多边形质心算法可快速提高VFVP算法的前期收敛速度。

如图8所示，4种不同节点数量条件下的4种算法的最终覆盖率对比中，VFVP在节点数量条件下的覆盖对比算法中取得了较好的覆盖率，VFVM算法的覆盖率增长图与VF算法接近，验证了Minmax算法对于VFVP算法的有效性，VFC算法在节点数量较小时覆盖率较小，随着节点数量增加，其覆盖率增长最快，可提高VFVP算法的收敛速度。

4 结束语

本文算法采用虚拟力算法为基础，几何Voronoi算法、质心算法、Minmax算法为辅，有效优化了在虚拟力环境下易陷入局部最优的问题，提高了监测区域的覆盖率，加快了算法的收敛速度。仿真实验验证了本文算法的有效性，采用的VFVP算法比原始虚拟力算法提高了约5%覆盖率。下一步将会在本文算法的基础上引入障碍物的情况，并进行相关减小覆盖重合区域的工作。

图7 收敛速度对比

图8 节点数目增加过程中的覆盖率增长

[1]SUN Zeyu,WU Weiguo,WANG Huanzhao,et al.An enhanced coverage control algorithm for wireless sensor networks based on adjustable parameters[J].Chinese Journal of Electronics,2015,43(3):466-474(in Chinese).[孙泽宇,伍卫国,王换招,等.无线传感器网络基于参数可调增强型覆盖控制算法[J].电子学报,2015,43(3):466-474.]

[2]WANG Changzheng,MAO Jianlin,FU Lixa,et al.Coverage optimization algorithm for three-dimensional directional heterogeneous sensor network[J].Journal of Computer Applications,2016,36(9):2362-2366(in Chinese).[王昌征,毛剑琳,付丽霞,等.面向三维的有向异构传感器网络覆盖优化算法[J].计算机应用,2016,36(9):2362-2366.]

[3]FAN Xinggang,YANG Jingjing,WANG Heng.Algorithm for enhancing probabilistic coverage in wireless sensor network[J].Journal of Software,2016,27(2):418-431(in Chinese).[范兴刚,杨静静,王恒.一种无线传感器网络的概率覆盖增强算法[J].软件学报,2016,27(2):418-431.]

[4]LIU Wei,HU Anlin.Reaserch of coverage ratio and energy saving in wireless sensor network[J].Application of Electronic Technique,2016,42(6):98-100(in Chinese).[刘伟,胡安林.无线传感器网络覆盖率与节能性研究[J].电子技术应用,2016,42(6):98-100.]

[5]WANG Lili,WU Xiaobei,HUANG Cheng,et al.Node scheduling strategy based on target coverage for heterogeneous directional sensor networks[J].Control and Decision,2016,31(12):2140-2146(in Chinese).[王力立,吴晓蓓,黄成,等.基于目标覆盖的异构有向传感器网络分布式节点调度策略[J].控制与决策,2016,31(12):2140-2146.]

[6]QIN Zefeng,TAN Ying,ZHAO Jing,et al.Research on coverag algorithm in wireless sensor network based on the Voronoi[J].Journal of Taiyuan University of Science and Technology,2013,34(3):185-190(in Chinese).[秦泽峰,谭瑛,赵静,等.基于Voronoi图的无线传感器网络覆盖算法研究[J].太原科技大学学报,2013,34(3):185-190.]

[7]Mahboubi H,Aghdam A G.Distributed deployment algorithms for coverage improvement in a network of wireless mobile sensors:Relocation by virtual force[J].IEEE Transactions on Control of Network Systems,2016,PP(99):1-1.

[8]HUANG Sheng,LIU Guangzhong,XU Ming.Distributed Voronoi control strategy based on virtual force[J].Computer Science,2016,43(10):125-129(in Chinese).[黄胜,刘广钟,徐明.一种基于虚拟力的分布式Voronoi控制策略[J].计算机科学,2016,43(10):125-129.]

[9]Abo Zahhad M,Sabor N,Sasaki S,et al.A centralized immune-Voronoi deployment algorithm for coverage maximization and energy conservation in mobile wireless sensor networks[J].Information Fusion,2016,30(C):36-51.

[10]Pietrabissa A,Liberati F,Oddi G.A distributed algorithm for Ad-hoc,network partitioning based on Voronoi tessellation[J].Ad Hoc Networks,2016,46:37-47.

[11]Le D V,Oh H,Yoon S.VirFID:A virtual force (VF)-based interest-driven moving phenomenon monitoring scheme using multiple mobile sensor nodes[J].Ad Hoc Networks,2015,27:112-132.