同时含有预防接种和水源处理的霍乱时滞模型分析*

廖 书， 杨炜明

(重庆工商大学 数学与统计学院，重庆 400067)

越来越多的研究者利用数学模型来构造传染病模型以对其进行定量和定性的研究，参见文献[1-6]。为了进一步控制水源性传染病的流行，以霍乱传染病为代表，首先考虑霍乱弧菌在不洁水源中会存活一段较长的时间，即增加时滞的考量，其次预防接种和利用消毒剂消毒不洁水源都是控制霍乱传播的有效手段，建立并研究一个同时含有预防接种和消毒不洁水源双重控制策略的霍乱时滞模型，最后采用2008年津巴布韦霍乱的数据进行数值模拟以研究这两种控制方法的有效性以及时滞大小对模型稳定性的影响。

1 霍乱时滞模型

设总人数N=S+I+V+R，且总人口数与饮水的供给和成正比，S，I，V和R分别表示易感染者、染病者、接种疫苗者和移出者，W为霍乱病菌浓度，T为消毒剂在水源中的浓度。消毒剂可以很有效地杀死水源中的霍乱弧菌并且控制其传播，假设消毒剂的浓度与失效率成正比，也与水源中霍乱病菌浓度成正比。再假设消毒剂的自然丧失率与其浓度成比例，且消毒剂摄取了霍乱弧菌后，其吸收率是与病毒的密度以及消毒剂的浓度成比例的。模型中其他的参数βI和βW分别表示环境与人之间传播和人与人之间传播的传染率系数，μ1和μ分别表示感染者和非感染者不同的死亡率，φ为疫苗接种率，α为消毒剂的失效率，π为霍乱病菌的增长率，ξ为霍乱病菌的自然丧失率，d为作为安全用水提供给住户的水源中霍乱病菌的丧失率，χ为当使用了消毒剂后霍乱病菌浓度的丧失率，θ为使用消毒剂的浓度，η为消毒剂在水源中的有效吸收率，γ为染病者的复原率，τ表示病菌在不洁水源中的潜伏期。σ表示疫苗的有效率，当σ=0为该疫苗完全有效，σ=1意味着疫苗没有效果。所有的参数都为正数。

(1)

(2)

(3)

(4)

(5)

(6)

模型的初始条件如下:

S≥0，I≥0，V≥0，W≥0，T≥0，R≥0

注意到系统方程中R的独立性(在式(1)—式(5)中均不含有R)，所以为了简化计算，在后面的分析中只考虑式(1)—式(5)即可。

2 地方病平衡点

本节主要研究地方病平衡点X*=(S*，I*，V*，W*，T*)的稳定性。首先令s=S-S*，v=V-V*，i=I-I*，w=W-W*以及f=T-T*，其中s，i，v，w和f是围绕X*的微小扰动。令

在地方病平衡点的特征方程可计算得：

(7)

其中

以及

由Routh-Hurwize判别法，可以证明当τ=0时，地方病平衡点是局部渐近稳定的。因此处计算比较冗长，故省去计算， 直接得出以下定理:

定理1 当R0>0，τ=0时，系统模型式(1)—式(5)的地方病平衡点是局部渐近稳定的。

当τ>0时，设λ=iω是方程式(7)的一个根， 将λ代入方程式(7)并分离实部和虚部后，可得到下面的两个方程：

(8)

(9)

将方程式(8)和方程式(9)平方相加：

(10)

再令ω2=x得到:

(11)

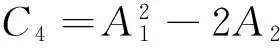
如果系数Ci满足Routh-Hurwitz条件，则方程式(11)不会有任何正根，因此不会得到满足方程式(8)和方程式(9)的正ω。在这种情况下有以下定理：

定理2 当R0>0，τ>0时，如果Routh-Hurwitz条件满足，系统式(1)—式(5) 的地方病平衡点是局部渐近稳定的。

(12)

对方程式(7)左右两边同时求λ关于τ的导数得到：

(13)

化简可得:

(14)

因此可以计算求得:

(15)

又由前面的假设条件C0<0可知，F'(x)>0，则上述方程一定大于0。即意味着当τ>τ0时，至少存在一个根有一个正实部并且从左向右穿过虚轴。因此当τ=τ0时，Hopf分支产生，并在τ=τ0附近产生一簇周期解。由文献[7，8]的Hopf分支定理，可以得到下面的定理：

定理3 当R0>0，时滞τ∈[0，τ0]时，如果Routh-Hurwitz条件满足，系统式(1)—式(5)的地方病平衡点是局部渐近稳定的；当时滞τ>τ0时，系统式(1)—式(5)不稳定。当τ=τ0时，系统在地方病平衡点产生Hopf分支，并在τ=τ0附近产生一簇周期解。

3 模型模拟

采用世界卫生组织发布的2008年—2009年津巴布韦霍乱的数据进行模型的数值模拟。津巴布韦的总人口大约12 347 240人， 为了计算方便，本节按比例减少1 200倍系数使得其总人口为1 000，模型中所用到的其他参数值为

N=10 000，μ=0.000 442，π=70
ξ=0.233 3，d=0.000 014，χ=0.99
α=1，θ=0.001，γ=1.4，σ=0.2
φ=0.003，βI=0.00 012，ψ=0.05
βW=0.000 000 42，η=0.000 4

同时初始条件在相应降低1 200倍之后为S0=9 890，I0=10，V0=100，T0=10和W0=0。

3.1 当τ=0时

把所有的参数代入R0的表达式，可求得R0=1.7，即在这种情况下，霍乱会在津巴布韦流行开来，并且最终地方病平衡点的值也可求得为(S*，I*，V*，R*) = (4 938.65， 0.442， 2 960.5， 2 100.2)，这与津巴布韦的霍乱传播实际情况相符合。图1和图2表示S*，I*，V*和R*随时间的变化趋势。

从图1可以观察到染病者人数在27周的时候达到最高峰72(除以1 200倍系数后的值)，然后直接下降到接近0，说明在进行有效的防疫之后，此次疫情已消除。考虑长期的情况，从图2可知，在第一次疫情爆发结束之后，还会有若干次疫情再度爆发，但最高峰值会越来越小，直到约384年后S*，V*和R*最终达到自己稳定值分别为4 938.65、2 960.5和2 100.2，此时在津巴布韦的霍乱才最终彻底消除。

图1 当τ=0时，随着时间的变化I的变化趋势

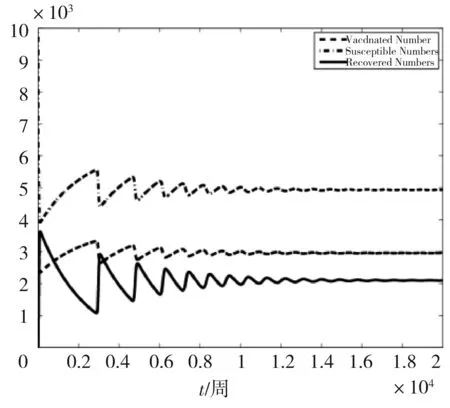
图2 当τ=0时，随着时间的变化S，V，R的变化趋势

图3和图4分别表示在没有预防接种和没有进行水源消毒的情况下染病者人数随时间变化的趋势。可以明显看出，在缺失预防接种或者水源消毒后，染病者人数明显高于图1中的染病者人数，说明这两种预防控制措施非常有效，都可以极大降低霍乱传播。

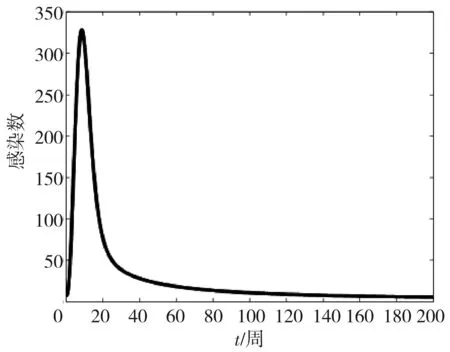
图3 缺失预防接种时，随着时间的变化I的变化趋势

图4 缺失水源消毒时， 随着时间变化I的变化趋势

3.2 当τ≠0时

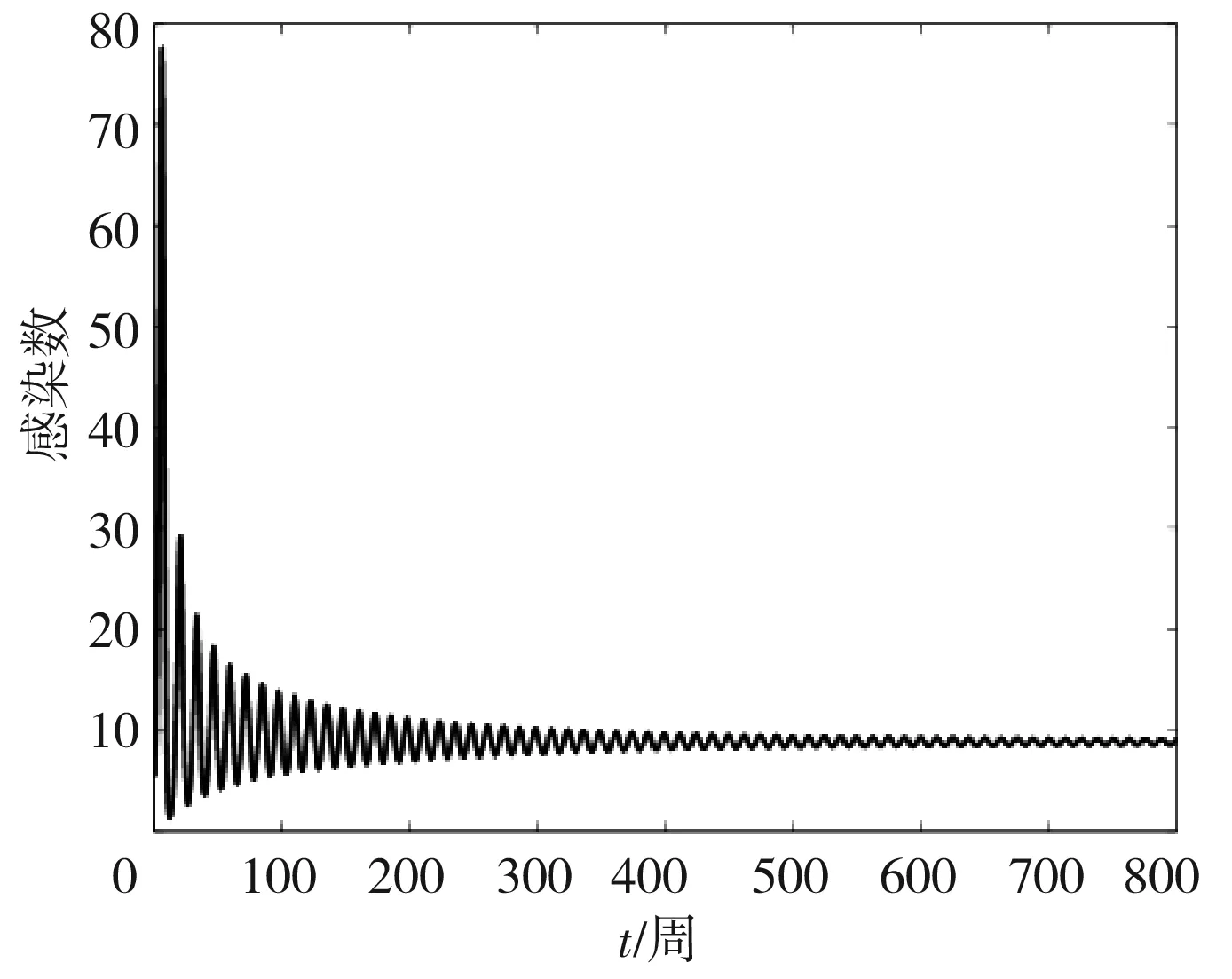
图5 当τ=2时，随着时间的变化I的变化趋势

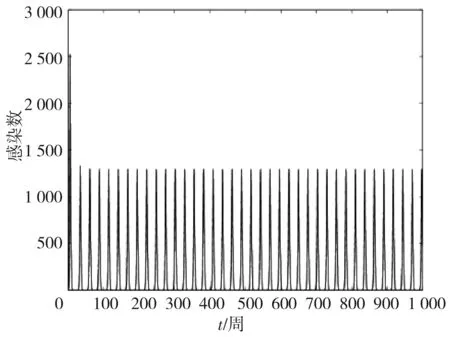
图6 当τ=4时，随着时间的变化I的变化趋势

在本节采用和上节同样的参数值和初始条件对τ≠0的情况进行数值模拟，此时时滞临界值τ0可求得为2.88。从图5可知，当取τ=2时，I*的振动逐渐降低并最终趋于它们分别的稳定值。然后当时滞大于阙值时，系统的稳定性会发生变化。

图6中，时滞取值为4时，可以看出I*开始发生不稳定的变化。说明对传染病进行模拟和预测时，在时滞变大的情况下，对未来的预测会变得更加困难。

4 结 论

建立并分析了一个同时含有预防接种和水源消毒的霍乱时滞模型。研究了模型地方病平衡点的稳定性，并通过分析相应特征方程根的分布，得出当时滞大小超过一个阙值的时候，稳定性发生变化，产生了Hopf分支，系统产生波动。结果说明了时滞模型比一般的ODE模型具有更大的现实意义，但计算上也更加困难。没有对地方病平衡点的全局稳定性进行证明，这将是未来工作之一。最后要注意尽管大剂量地进行水源杀毒可以在短时间内有效控制霍乱疫情的流行，但在现实生活中，大剂量的杀毒剂使用又会对人体健康造成巨大危害，因此要同时考量对人体健康和安全的因素，合理控制杀毒剂的使用。

[1] CODECO C T. Endemic and Epidemic Dynamics of Cholera: the Role of the Aquatic Reservoir[J]. BMC Infectious Diseases， 2001(1):1

[2] HARTLEY D M， MORRIS J G，SMITH D L. Hyperinfectivity:a Critical Element in the Ability of V Cholerae to Cause Epidemics[J]. PLoS Medicine， 2006(3):63-69

[3] JOH R I， WANG H， WEISS H，et al. Dynamics of Indirectly

Transmitted Infectious Diseases with Immunological Threshold[J]. Bulletin of Mathematical Biology， 2009， 71(4):845-862

[4] SANCHES R P， FERREIRA C P，KRAENKEL R A. The Role of Immunity and Seasonality in Cholera Epidemic[J]. Bulletin of Mathematical Biology， 2011，73(12):2916-2931

[5] LIAO S，WANG J. Stability Analysis and Application of a Mathematical Cholera Model[J]. Mathematical Biosciences and Engineering， 2011(8): 733-752

[6] TIEN J H， EARN D J D. Multiple Transmission Pathways and Disease Dynamics in a Waterborne Pathogen Model[J].Bulletin of Mathematical Biology，2010，72: 1506-1533

[7] GOPALSAMY K.Stability and Oscillations in Delay Differential Equations of Population Dynamics[M].Dordrecht：Kluwer Academic，1992

[8] HALE J K.Theory of Functional Differential Equations[M].New York: Spring-Verlag，1977