非线性晶体产生的空心光束中大尺寸粒子囚禁与导引∗

2018-03-19宁效龙王志章裴春莹尹亚玲

物理学报 2018年1期

宁效龙王志章裴春莹尹亚玲

(华东师范大学物理与材料科学学院,精密光谱科学与技术国家重点实验室,上海 200062)

1 引言

1970年,Ashkin[1]首次利用两束相向传播的激光束实现了对水中以及空气中微米量级的高折射率且光学稳定性良好的玻璃微球的二维囚禁与操控.1986年,Ashkin小组又首次成功地实现了基于单光束梯度力的三维粒子囚禁技术,他们采用聚焦透镜对光束进行聚焦,并成功地利用该强聚焦光束将处于水中的玻璃微球束缚在了光束焦点下方[2].自此,“光镊技术”(单光束梯度力势阱粒子俘获技术)正式产生,并逐渐走进众多科学家的视野之中.目前,科学家们已经成功地利用光镊技术实现了对纳米粒子[3]、原子[4]、生物细胞[5]的俘获.

在单光束梯度力阱理论中,光镊俘获粒子主要利用的是光辐射压力,该力是由于物体对光的吸收、散射、发射以及再辐射而产生的.光辐射压力包括散射力和梯度力两种:散射力的大小与入射光强成正比并指向光传播方向,梯度力的大小与光强的梯度成正比并指向光强的最强处,二者的合力决定粒子是否能被稳定地俘获[2].

尽管传统的基于光辐射压力的光镊技术可以很好地实现对部分微粒的俘获,但由于光辐射压力较弱,利用光辐射压力对粒子进行操控会严格受控于粒子的体积大小,而且操控粒子所能移动的空间距离也一般仅为几百个微米,因此不适合用于较大尺寸粒子(微米级)以及有较长距离要求的操控与运输.近年来,随着对大尺寸粒子操控技术的研究,一种新的操控力——光泳力逐渐走进人们的视野.当处于气体介质中的粒子的表面受到入射光的不均匀加热时,气体分子将会以不同的速度被粒子表面所弹回,进而对粒子产生一个宏观力,此即为光泳力.与光辐射压力相比,光束产生的光泳力要比相同光强情况下产生的光辐射压力大得多,因此,光泳现象使得利用光束对大尺寸粒子进行操控与囚禁成为可能[6].

随着激光技术的发展,激光光束形状种类越来越丰富,这些也使得基于光泳力的粒子操控的研究内容更加丰富.例如,利用粒子在空心光束内部受到的光泳力实现对空气中的碳纳米团簇的三维俘获与导引[7],利用锥形光纤实现SiO2粒子的囚禁、迁移与分离[8,9],利用激光散斑场俘获墨粉颗粒[10],利用贝塞尔-高斯光束中的光泳力囚禁与操控磁性微粒子[11],利用艾里光束叠加产生阵列空心光束囚禁吸收型玻璃碳粒子[12]等.最近,我们小组利用非线性ZnSe晶体产生尺寸可调的空心光束以及局域空心光束[13,14],基于此项工作,本文提出基于非线性ZnSe晶体产生的空心光束与光泳力的大尺寸粒子的二维囚禁与一维导引,以及三维囚禁方案,并进行相关的理论研究.我们的方案中空心光束尺寸大,可以对大量大尺寸粒子同时进行操控,也可进行微纳米颗粒检测、分离与筛选.研究结果表明,非线性ZnSe晶体产生的空心光束可以作为大尺寸粒子非接触式有效操控的工具,在现代光学与生物医学中有潜在的应用.

2 基于非线性ZnSe晶体产生的空心光束的大尺寸粒子的二维囚禁与一维导引

光泳现象实质上是由于微粒表面温度梯度而导致的微粒周围空气分子产生的一种热蠕变的现象.同时,微粒周围的空气分子可以被视为一种连续且具有滑移边界条件的流体介质.研究发现光泳力可以实现大尺寸粒子的操控与囚禁.基于此,我们提出一种基于非线性ZnSe晶体产生的空心光束的大尺寸粒子的二维囚禁与一维导引方案,具体如图1所示.一束高斯光束沿z方向传播并由透镜L1与L2准直,然后通过一块较薄的非线性ZnSe晶体.在ZnSe晶体后可以得到经由ZnSe晶体非线性效应整形而得到长距离稳定传输的单向封闭的空心光束[14].本方案中,整套装置都处于空气介质中.空心光束之所以能够实现基于光泳力的粒子囚禁,是由于其横向中心光强为零的特殊性质.粒子处于空心光束中心及内部时,横向上会受到来自光束所引起的横向光泳力以及自身所受的重力作用.当满足一定条件时,二者的合力指向光束中心,从而会对粒子产生一个横向二维囚禁的作用.纵向方向上,粒子会受到光束所引起的纵向光泳力、光辐射压力以及空气介质所产生的黏滞阻力作用.研究表明,相同的入射光功率下,光束内粒子受到的光泳力要比光辐射压力大4—5个数量级[15],因此光辐射对粒子的作用力可以忽略不计.由于粒子所受到的来自空气介质的黏滞阻力远小于光束引起的光泳力,因此粒子会在纵向光泳力的作用下沿纵向光泳力方向,即光束传播方向运动,从而实现大尺寸粒子的纵向一维导引.因此,该方案可以同时实现大尺寸粒子的横向二维囚禁与纵向一维导引.

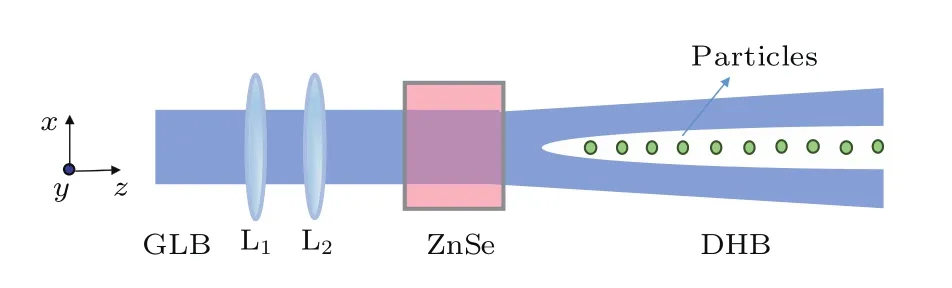
图1 基于非线性ZnSe晶体产生的空心光束的大尺寸粒子的二维囚禁与导引方案示意图,其中GLB是入射高斯光束,DHB是空心光束Fig.1.Schematic diagram of 2D trapping and guiding large-size particles using a hollow beam generated by a nonlinear ZnSe crystal.GLB and DHB are an incident Gaussian laser beam and a dark hollow beam,respectively.

空心光束照射粒子所产生的光泳力(FPP)为[7]

式中I是空心光束的光强,µa是气体的黏度系数,a是粒子的半径,ρa是粒子的质量密度,T是环境温度,ka和kf分别是气体和微粒的导热系数,J1是与粒子吸收长度有关的常系数.光泳力的产生要求微粒具有极低的反射率与导热系数,本方案研究中使用碳纳米团簇泡沫作为被囚禁粒子,并将其理想化为球形粒子,其质量密度ρa=0.00129 g·cm−3,导热系数kf=0.0266 W·m−1·K−1[16].

之前的研究工作中,我们得到了在沿z轴距ZnSe晶体不同距离的传播位置z处的光束的归一化光强与二维光场分布[13]. 其中,使用的入射高斯光束的束腰半径w0=300µm,光场振幅为光束的波长为λ=447.6 nm,ZnSe晶体的厚度为L=450µm.计算结果表明:当z=0.62 m时,可以得到最佳空心光束,在离开最佳位置一段范围保持为发散的空心光束.选取z=0.62 m处的最佳空心光束进行拟合,拟合公式为TEM01模的拉盖尔-高斯光束表达式[17]:

式中P为入射光功率,ρ是光束截面上的某点距光束中心的距离,w是光束截面半径.经拟合,得到z=0.62 m处的最佳空心光束的光强表达式中参数w=0.56 mm.将拟合出的光束截面半径w与理论值(≈0.57 mm)进行比较,可以发现拟合得到的公式与数值计算得到的空心光束能较好地符合.

以(2)式中的空心光束为例,从纵向与横向两个方向,对基于光泳力的空心光束中粒子二维囚禁与导引进行理论计算、分析与讨论.

2.1 纵向光泳力

光泳力本质上是一种热学力,光泳力通过作用于粒子周围的气体分子,引起气体分子的运动状态的变化,进而影响粒子的运动状态.光束传播方向(也就是纵向方向)上,引入一个动量流参数M,且|M|=kI,其中k为光泳效率,为一常数.取粒子的一个纵向截面进行分析(如图2所示),由定义可知,光泳力可以由动量流M对球面积分得到,即其中dS= πa2sinθdθ.由此,纵向光泳力FL可以描述为

式中ML=−kI(S+)cosθ,S+指的是受到光照的半球面,θ满足π/2≤θ≤π,纵向光泳力的方向与光束传播方向(图2中的z轴方向)一致.

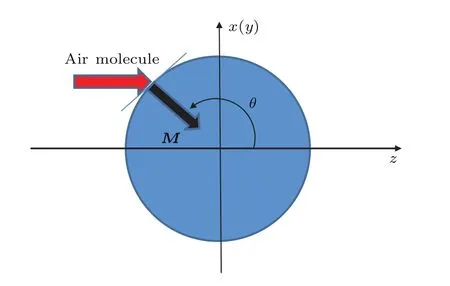
图2 空心光束通过作用于气体分子对粒子传递动量示意图Fig.2.Schematic diagram describing the transfer of a momentum from a gas molecule to a particle in the hollow beam.

当光束为光强等于I0的平面波时,

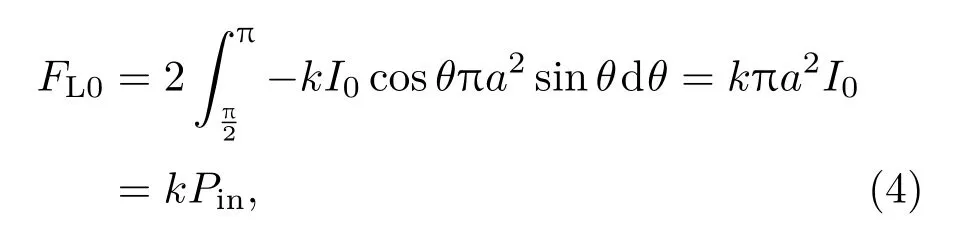
式中Pin0为有效光束光功率,且

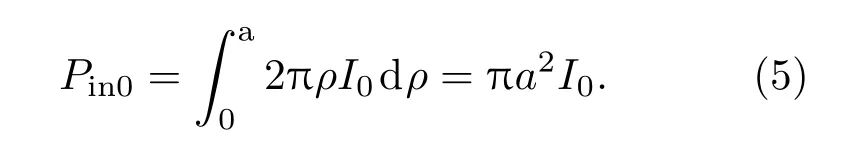
对于平面波,其对粒子产生的横向光泳力必为0,因此将(4)式与(2)式相比较,可以得到光泳效率κ的表达式为

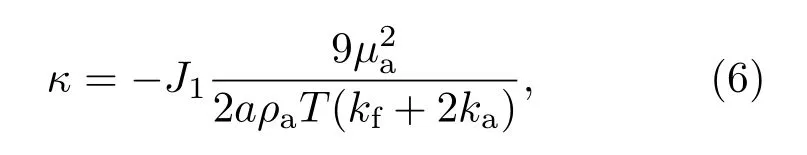
式中气体黏度系数µa=1.73×10−5N·s·m−2,粒子的质量密度ρa=1.29 mg·cm−3, 环境温度T=298 K,气体和微粒的导热系数分别为ka=0.0262 W·m−1·K−1和kf=0.0266 W·m−1·K−1,微粒的吸收长度lf=35µm,J1=−2a/(3lf)[15].将其代入上式可得光泳效率:κ=8.5×10−7s/m.

当入射光为(2)式所示的空心光束时,可得FL=κPin,式中Pin为有效空心光束光功率,假设微粒球心与光束中心重合,则

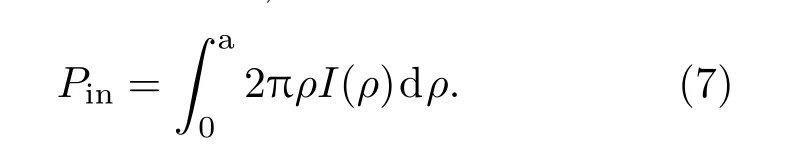
虽然微粒具有一定的厚度,但由于被囚禁的微粒的半径一般远小于光束的束腰半径,因此可以在光束传播方向上将微粒看作是没有厚度的圆面,这样很大程度上简化了后续的计算.因此,空心光束的有效入射光光功率为

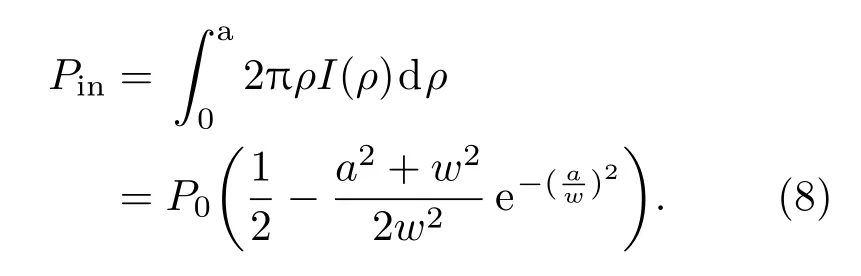
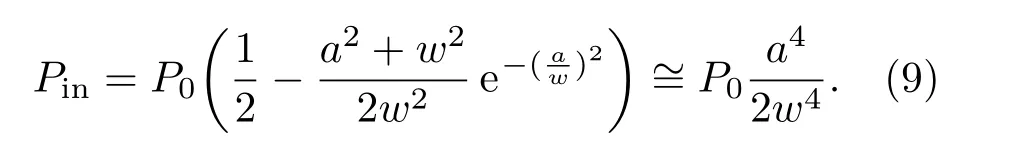
故空心光束中微粒所受的纵向光泳力为

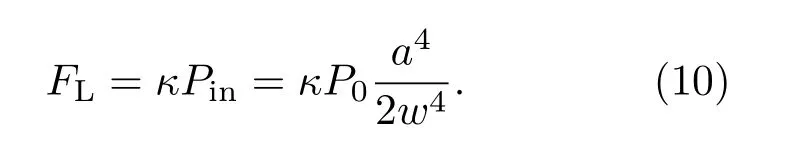
上式说明纵向光泳力的大小同粒子尺寸与光束尺寸比例的四次方成正比,与空心光束功率成正比,方向与光束传播方向(z轴方向)一致.

2.2 横向光泳力

截取球形微粒的某一横向截面(即与光束传播方向z轴方向相垂直的截面)进行受力分析(记该横向截面的半径为ρ),如图3所示.假设微粒球心与空心光束的中心不重合,设球心到光束中心的距离为R,则该截面圆周上每个点所受到的横向光泳力|M′|不能互相抵消,从而会产生一个由微粒球心指向空心光束中心的一个宏观力F⊥,且圆周上每一点所受到的横向光泳力呈轴对称分布.为了简化计算,以微粒的中心为原点建立直角三维坐标系,且使y轴与F⊥方向重合.对纵向光泳力的分析可以类比,|M′|满足

对一个球形微粒模型进行分析可以得到sinθ=ρ/a,故

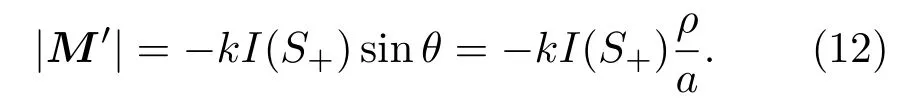
相应的横向光泳力为

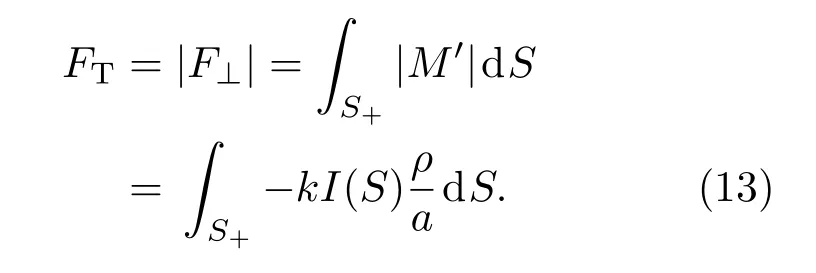
图3 横向截面上粒子的受力情况Fig.3.The force analysis of particle in the transverse plane.

综合以上各式,微粒所受到的横向光泳力FT为

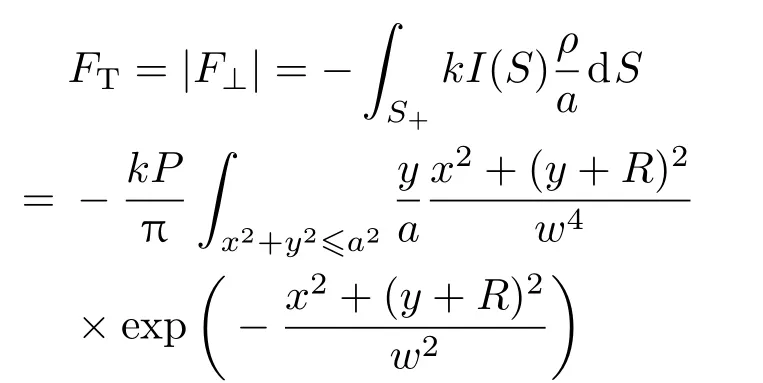
分析(14)式可以发现πFT/kP可以看作是关于两个主要参数R/w和a/w的函数,代入具体参数后计算结果如图4所示.观察图4(a)可以明显地看到以R=w为分界的两部分:1)R＜w时,空心光束对粒子产生囚禁效果的宏观光泳力;2)R＞w时,空心光束外围对粒子产生排斥力.同时除了在R=0处存在一个平衡位置外,在R=w处同样存在一个不稳定的平衡点.当a/w越大,也就是粒子尺寸与空心光束尺寸越接近时,横向光泳力越大.观察图4(b)可以看出,对于尺寸较小的粒子,其所受到的横向光泳力皆为囚禁力,粒子总是被束缚在光轴附近;对于尺寸大于光束半径a＞w的粒子,空心光束对其的束缚作用很快地消失.空心光束对粒子的最大束缚力出现在a=0.95w附近.假设空心光束光功率为P=1 W,粒子半径为a=300µm,且已知光束截面半径为w=560µm,即由图4(a)可以看出此时粒子在空心光束内所可能受到的最大横向光泳力出现在R=0.5w处,其值为而粒子的重力约为可以看出FTmax比G高出一个量级,即粒子在空心光束内部距中心一定距离范围内,其所受到的横向光泳力完全可以抵消其所受到的重力.因此,粒子在空心光束内部时,一方面它会受到来自光束的横向囚禁作用力而向光束中心运动,另一方面,粒子由于其自身受到的重力会向远离光束中心的方向运动.粒子在重力的作用下由光束中心逐渐向光束外部运动的过程中,其所受到的横向拘禁力会逐渐增大,最终粒子还会往光束中心运动,粒子处于一个相对动态平衡的状态,从而空心光束可以实现对该大尺寸粒子的横向二维囚禁.

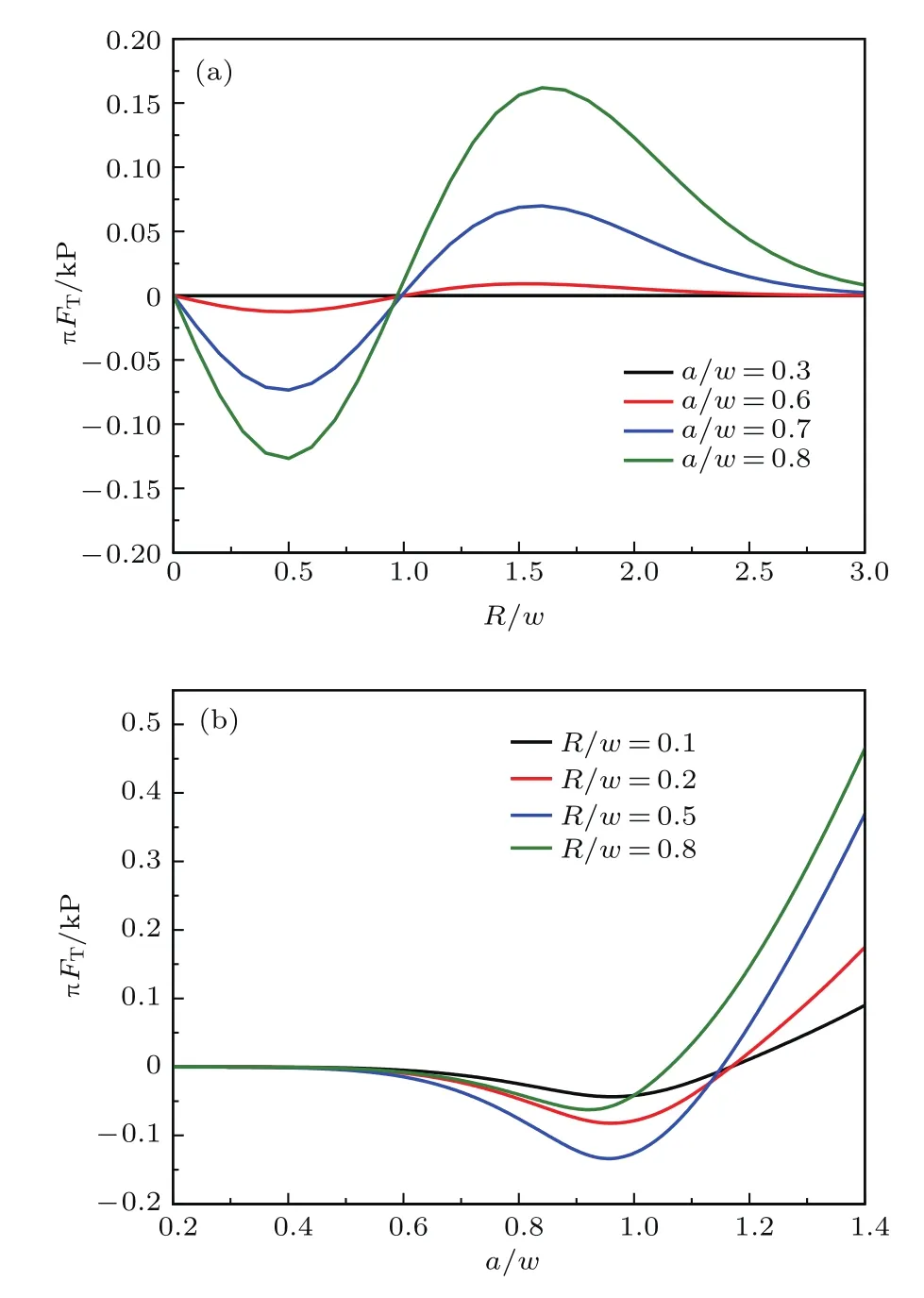
图4 (a)πFT/kP和R/w之间的关系;(b)πFT/kP和a/w之间的关系Fig.4.(a)πFT/kP versus one of key parameters R/w;(b)πFT/kP versus one of key parameters a/w.

2.3 粒子导引

之前的研究表明,在z=0.1—0.8 m的范围内,光束始终处于一个“中空”的状态,即中心光强很弱而周围光强较强,同时每一个z处的光束截面半径变化较小,比较均匀[13].而当z＞1 m以后,光束的截面半径与中心光强均快速增大.因此,可以考虑将z=0.1—0.8 m范围内的光束看作是一个导管,其在横向截面内受到的合力指向光束中心,使得粒子横向上被囚禁在光场的空间范围内.粒子在导管内受到的纵向光泳力的分布如图5所示.由于纵向光泳力与光场功率成正比,空心光束横向分布存在两个光场极大值点,所以纵向光泳力在光场极大值点最大,其他位置变小(如图5所示,图中箭头标识的粗细与受力大小呈正相关).由图5可知,纵向光泳力的方向与空心光束传播方向相同,粒子在纵向光泳力的作用下沿光场方向运动.也就是说处于空心光束中的粒子横向被囚禁的同时,纵向被光泳力引导着向光束传播的方向运动,即一维定向导引.因此,利用光束对粒子的纵向光泳力,可以实现对大尺寸粒子的纵向一维定向导引.

图5 ZnSe晶体后距离为z=0.1—0.8 m处输出光束在xoz截面内纵向光泳力示意图Fig.5.Schematic diagram of longitudinal forces of the light beam output from the nonlinear ZnSe crystal for a distance z=0.1–0.8 m in the xoz plane.

接下来理论分析粒子导引动力学过程.当粒子在光束的中心沿z方向运动时,在z方向上除了会受到光束的纵向光泳力FL外,还会受到来自周围空气介质的黏性阻力S(流体介质的黏性阻力S=−6πµav,式中µ=1.73×10−5N·s·m−2为气体的黏度系数).当粒子匀速运动时,必然满足FL+S=0,即FL=−6πµav.微粒运动的平均速度可以由下式描述:

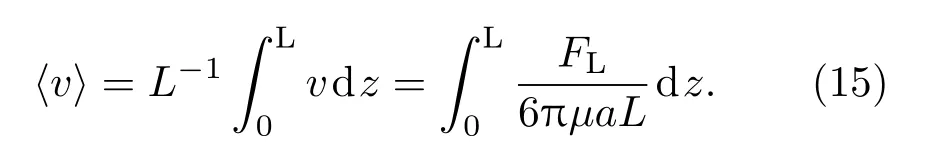
由于在z=0.1—0.8 m的范围内,光束的截面半径与光强等参数变化均不大,因此可以将该范围内粒子所受的纵向光泳力近似看为不变,相应的表达式为则粒子在“导管”内的平均速度为

由(16)式可以看出,粒子的运动速度与粒子的半径在一定的范围内呈立方关系.假设入射光功率为P=1 W,截面半径为w=560µm,粒子半径为a=300µm,则粒子在“导管”内的平均速度约为35.8 cm/s.因此,该“导管”可以实现对大尺寸粒子的长距离(米量级)高速定向导引.

3 基于双非线性ZnSe晶体产生的局域空心光束的大尺寸粒子的三维囚禁

局域空心光束(localized hollow beam,LHB)是一种在沿传播方向的三维空间内具有封闭暗域的特殊空心光束,且暗域周围的光束具有极高的强度.在我们近期的工作中,提出了一种基于双非线性ZnSe晶体整形后干涉而形成局域空心光束的方法[14],数值结果表明该局域空心光场分布以z=0.2 m为中心呈对称分布,且光束纵横比可调[14].根据上面对单个非线性晶体产生的空心光束中大尺寸粒子囚禁与导引方案的分析,局域空心光束中的粒子所受到的横向光泳力同样可以实现粒子的横向囚禁.由于局域空心光束是由两束相反传输的光束叠加而成,且光强为对称中心最大,所以粒子在纵向受到的光泳力使得粒子往局域空心光束中心运动,从而实现纵向囚禁.综上,该局域空心光束可以实现大尺寸粒子的三维囚禁.

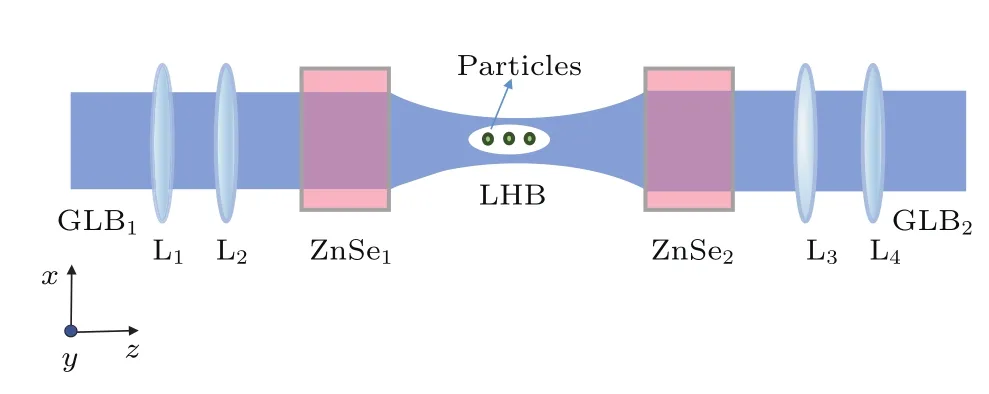
图6 基于双非线性ZnSe晶体整形的局域空心光束的产生装置简图 GB是入射高斯光束;C1,C2是非线性ZnSe晶体;L1,L2是透镜Fig.6.The schematic diagram of generating a localized hollow beam based on double nonlinear ZnSe crystals.GB is Gaussian laser beam;C1,C2are nonlinear ZnSe crystals;L1,L2are lenses.

3.1 横向光泳力

对z=0.2 m处的光束截面中的光强分布进行模拟,同样可以得到该分布的近似表达式为

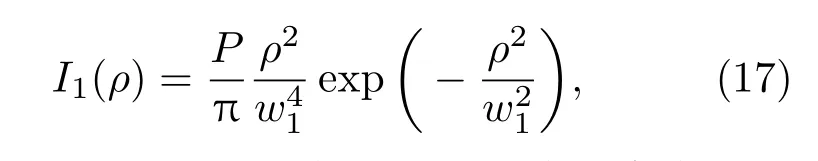
式中w1=0.34 mm.因此,xoy平面内距离中心距离为R处半径为a的粒子所受到的横向光泳力为

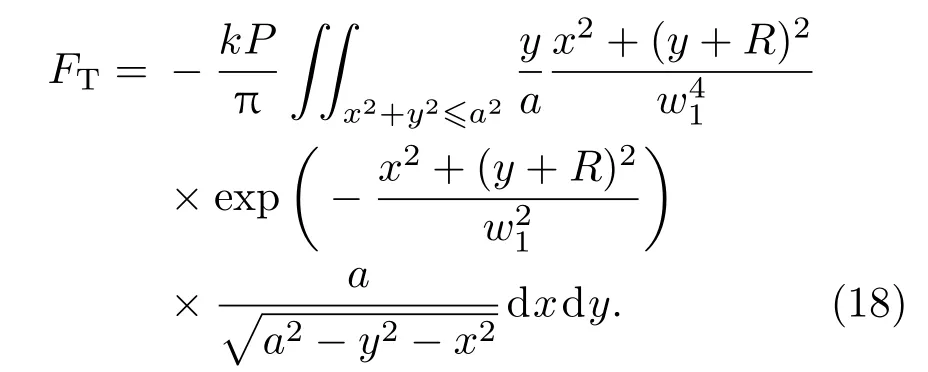
根据数值计算结果,同样可以给出πFT/kP关于两个主要参数R/w和a/w的函数,如图7所示.由图7可以看出,与图4中反映的空心光束中粒子的受力情况类似,当粒子与局域空心光束中心之间距离R＜x时,光束将对粒子产生指向光束中心的拘禁力;当R＞x时,光束将对粒子产生指向光束外部的推力.我们假设入射光功率为P=1 W,粒子的半径为a=300µm,则根据图7可以大致计算得到粒子在局域空心光束内受到的最大横向光泳力约为FTmax=8.12×10−8N,而粒子的重力约为同样满足FTmax≫G.根据2.2节中的分析可以得知在该三维封闭椭球局域空心光束的中心截面内可以成功实现对粒子的二维囚禁.

图7 (a)πFT/kP和R/w之间的关系;(b)πFT/kP和a/w之间的关系Fig.7.(a)πFT/kP versus one of key parameters R/w;(b)πFT/kP versus one of key parameters a/w.

3.2 纵向光泳力

在第2.2节中我们已经得到粒子在空心光束内受到的纵向光泳力与粒子表面照射到的光功率成正比关系,可以绘出在该局域空心光束的xoz截面内相应位置处粒子所受到的纵向光泳力大小与方向的示意图,如图8所示(图中箭头标识的粗细与粒子受力的大小成正比,方向与受力方向相同).由于局域空心光束是由两束相反传输的光束叠加而成,且光强为对称中心最大.在左边区域,粒子受到的光泳力指向右,在右边区域,粒子所受到的光泳力指向左.因此纵向光泳力可以实现粒子的纵向囚禁.观察图8可以看出,当粒子处于局域空心光束的中心时,由于局域空心光束内光强分布关于中心截面(xoy截面)完全对称,因此其受到的横向光泳力与纵向光泳力都可以完全抵消,从而粒子可以稳定地被囚禁在光束的中心处.同时,被囚禁粒子的半径可以达到几百个微米的量级,远远超出了以往基于光辐射梯度力的粒子囚禁技术所能囚禁的粒子的尺寸极限.因此,基于双非线性晶体法产生的局域空心光束可以很好地实现对大尺寸粒子的三维囚禁.

图8 基于双非线性晶体整形产生的局域空心光束在xoz平面内的纵向光泳力分布示意图Fig.8.Schematic diagram of longitudinal forces in the xoz plane of LHB reshaped by two nonlinear crystals.

4 结论

比较第2节中基于单ZnSe晶体整形产生的空心光束与第3节中基于双非线性ZnSe晶体产生的局域空心光束对粒子的囚禁情况,我们可以得出以下结论:两者都可以实现对大尺寸粒子的横向二维囚禁,空心光束内粒子受到的纵向光泳力的大小同粒子尺寸与光束尺寸比例的四次方成正比,与空心光束功率成正比,方向与光束传播方向一致.粒子尺寸与空心光束尺寸越接近时,横向光泳力的大小越大.但与利用单非线性ZnSe晶体整形产生的空心光束相比,利用双非线性ZnSe晶体产生的局域空心光束可以实现对粒子的三维囚禁,因此其拥有更好的囚禁能力,在粒子囚禁方面也有着更为广阔的应用前景.虽然基于单ZnSe晶体整形产生的空心光束只能实现对粒子的二维囚禁,但是可以利用其对粒子在光束传播方向上进行长距离(米量级)的高速粒子导引.总之,基于上述分析与讨论,本文提出的基于非线性晶体产生的空心光束与光泳力的大尺寸粒子囚禁与导引方案具有可行性,可以用于单个或者多个大尺寸粒子的非接触式、无损伤囚禁与导引.囚禁的大尺寸粒子可以用于光谱、碰撞、环境监测、生物检测等方面的研究.

[1]Ashkin A 1970Phys.Rev.Lett.24 156

[2]Ashkin A,Dziedzic J M,Bjorkholm J E,Chu S 1986Opt.Lett.11 288

[3]Dienerowitz M,Mazilu M,Dholakia K 2008J.Nanophoton2 021875

[4]Chu S 1998Rev.Mod.Phys.70 685

[5]Ashkin A,Dziedzic J M,Yamane T 1987Nature330 769

[6]Davis E J,Schweiger G 2002The Air Borne Microparticle:Its Physics,Chemistry,Optics,and Transport Phenomena(Heidelberg:Springer)pp780–785

[7]Shvedov V G,Desyatnikov A S,Rode A V,Krolikowski W,Kivshar Y S 2009Opt.Express17 5743

[8]Xin H B,Li X M,Li B J 2011Opt.Express19 17065

[9]Xin H B,Bao D H,Zhong F,Li B J 2013Laser Phys.Lett.10 036004

[10]Zhang Z G,Liu F R,Zhang Q C,Cheng T,Wu X P 2014Acta Phys.Sin.63 028701(in Chinese)[张志刚,刘丰瑞,张青川,程腾,伍小平2014物理学报63 028701]

[11]Gong L,Liu W W,Zhao Q,Ren Y X,Qiu X Z,Zhong M C,Li Y M 2016Sci.Rep.6 29001

[12]Zhang Z,Zhang P,Mills M,Chen Z G,Christodoulides D N,Liu J J 2013Chin.Opt.Lett.11 033502