基于分数阶最大相关熵算法的混沌时间序列预测∗

王世元 史春芬 钱国兵 王万里

1)(西南大学电子信息工程学院,重庆 400715)

2)(非线性电路与智能信息处理重庆市重点实验室,重庆 400715)

1 引 言

混沌系统对初始值敏感的特性使输入信号的微小变化均能快速体现在输出信号中,所以混沌模型更能反映现实世界的真实情况,即混沌理论提供了一种符合现实世界的非线性建模方法.随着混沌理论和应用技术研究的不断深入,混沌时间序列的建模和预测已成为近年来混沌信号处理领域的一个重要热点[1−5].然而,混沌系统对初始值敏感的特性使得混沌时间序列不能长期预测.但混沌时间序列是由确定性非线性系统产生的,其内部存在确定性规律,所以混沌时间序列是短期可预测[6].由此可见,混沌时间序列预测是一个极具挑战性的工作.高效的预测模型可广泛应用于混沌去噪,混沌加密以及混沌通信等领域中.Takens的嵌入定理[7]提供了预测混沌时间序列的理论依据.基于Takens的嵌入定理和相空间重构思想,混沌时间序列预测方法可分为全局预测方法[3]、局域预测法[4]和自适应预测法[5]三大类.全局预测法采用全部已知数据拟合非线性函数,但当非线性函数关系较复杂时,这种方法不能精确拟合非线性函数.局域预测法仅利用相空间中部分数据拟合非线性函数,即利用当前数据最近邻域点的演化轨迹加权预测未来数据,因只采用了部分数据,所以局域预测法可提供较快的运算速度,但对未知数据区间的预测精度较差.自适应预测法是近年来兴起的混沌时间序列预测方法,在预测过程中只需较少的训练样本就能对混沌序列做出较好的预测结果.

自适应滤波算法是一类经典的自适应算法,现已被广泛应用于噪声消除、信道均衡和系统识别等领域中[8].根据不同的误差准则可以生成不同的自适应滤波算法,包括最小化均方算法(least mean square,LMS)[9]、仿射投影算法(affine projection algorithm,APA)[10]和递归最小二乘(recursive least squares,RLS)[11]算法.LMS算法因采用当前瞬时平方误差作为误差准则,其计算最为简单,是广泛应用于实际的经典自适应滤波算法.尽管LMS算法具有低复杂度和易实现的特点,但其收敛速度较慢.APA算法利用过去一段时间和当前时刻的数据更新权重，因此相对于LMS算法,APA算法以增加一定的计算复杂度为代价提高了滤波器的预测速度和精度.基于最小二乘(least squares,LS)[12]的RLS算法利用所有输入数据更新滤波系统,因此具有更好的滤波性能,但其计算复杂度也更高.以上三种经典的自适应滤波算法均采用最小均方误差(minimum mean square error,MMSE)准则.因此,在非高斯噪声环境下它们不能获得较理想的滤波性能.然而,实际环境中的大多数噪声具有显著的脉冲性特点.因此,提出了适应非高斯噪声的误差准则及其相应的自适应滤波器,例如,基于最小误差熵(minimum error entropy,MEE)[13]的自适应滤波器.MEE是一种非凸的代价函数,需要Parzen窗去估计每一个时刻的误差分布[14],因此,基于MEE准则的自适应滤波器具有较高的计算复杂度.为了减小其计算复杂度,提出了另一种基于最大相关熵准则(maximum correntropy criterion,MCC)[15]的自适应滤波器.MCC因其计算效率高和处理非高斯信号能力较强，已被广泛应用于信号处理和机器学习等领域[15−17].与基于MMSE准则的自适应滤波算法相比,当系统噪声为非高斯噪声或者输入数据有较大的奇异值时,基于MCC准则的自适应滤波算法具有较好的鲁棒性.

随着分数阶微积分的不断发展,作为分数维动力学基础的分数阶取得了极大的进展.整数阶微积分仅仅决定函数的局部特征,而分数阶微积分以加权的形式考虑了函数的整体信息,因此可以更准确地描述实际系统的动态响应,最终可实现预期的鲁棒性、稳定性、良好的动态性能和滤波精度[18].目前,分数阶已被广泛应用在控制和信号处理等领域[19−21].在一个分数阶系统中,输入和输出是根据一个非整数阶的微分方程联系,这里的非整数阶数可以是正的、负的甚至是复数.

受基于MCC准则的自适应滤波算法的鲁棒性以及分数阶微积分的普适性的启发,本文根据混沌时间序列的短期可预测性在MCC准则的基础上引入分数阶,提出一种新的自适应滤波算法——分数阶最大相关熵(fractional-order maximum correntropy criterion,FMCC)算法,在增加一定计算量的前提下,FMCC算法能够在混沌时间序列预测方面实现更快的收敛速度和更低的稳态误差,进而实现更好的预测结果.

2 背 景

2.1 最大相关熵算法

相关熵(correntropy)[22,23]是指两个随机变量X和Y相似度的非线性测量,定义为

其 中,k(·,·) 是 受 核 宽 度σ控 制 的Mercer核,PX,Y(x,y)表示X和Y的联合概率密度函数.由于高斯核[24,25]具有普适的逼近能力,因此通常将其作为相关熵的核函数.高斯核的定义为

其中,e=x−y,且σ＞0.

然而,在实际应用中,联合概率密度函数PX,Y(x,y)总是未知的,且可使用的数据是有限的.因此,通常用样本的估计量去近似表示(1)式中的期望,即

结合随机梯度方法[11],MCC算法的权重更新方式为

其中,µMCC是MCC算法的学习步长.

结合(4)式和(5)式可以看出,当外界所加噪声为脉冲噪声时,(4)式代价函数的导数趋于零,即(5)式中的权重不更新.因此,MCC算法能够有效抑制脉冲噪声的影响,具有较好的鲁棒性.

2.2 分数阶微积分

分数阶微积分理论几乎与整数阶微积分理论具有同样长的发展历史.因采用分数阶微积分描述的系统能够更接近实际系统,所以近年来引起人们的广泛兴趣和深入研究.在分数阶微积分的研究过程中,对分数阶微分有多种定义,如Grunwald-Letnikov定义、Riemann-Liouville(RL)定义和Caputo定义[26,27].本文所用的是RL定义[27],包括积分和微分.

对于函数f(t),RL分数阶积分的定义如下:

其中,Iv是指v阶积分,实数v∈(0,1)表示阶数;Γ表示伽马函数.对于z−v+1＞0,伽马函数Γ可表示为

且

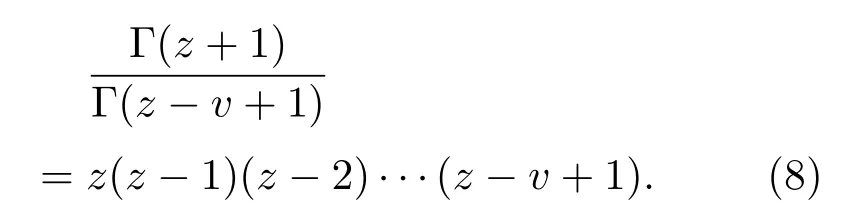
同样,v阶RL微分的定义可描述为

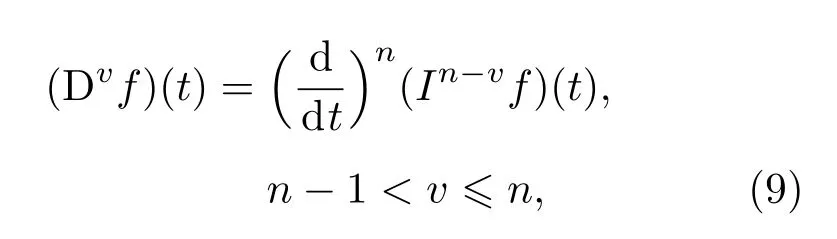
其中,Dv表示v阶微分,n为整数.

将(6)式代入(9)式即为

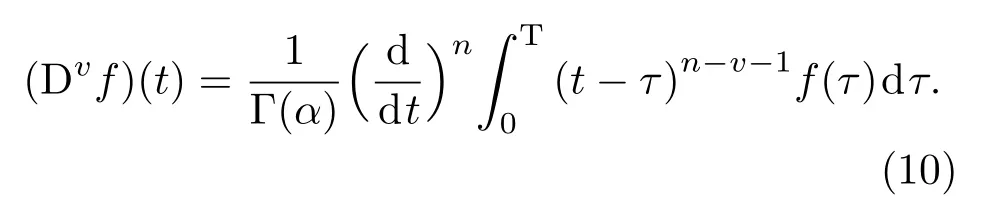
以函数f(t)=(t−b)α为例,它的分数阶导数具体表示为

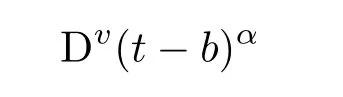
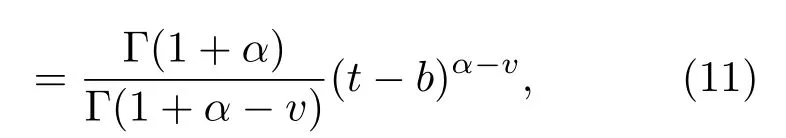
其中,b和α为常数.

3 分数阶最大相关熵算法

在采用随机梯度更新权重的自适应滤波器算法中,例如,LMS和MCC算法等,均需设置一个较小的学习步长用以保证算法收敛到一个较小的稳态误差.然而较小的学习步长同时会导致较慢的收敛速度,即增加算法收敛到最优权重的迭代步数.为解决这一问题，基于分数阶的梯度更新方法能够在增加一定计算复杂度的前提下提高滤波性能[19],目前,该方法已成功应用于LMS算法中提高了其滤波性能和收敛速度.因此,本文在MCC准则的基础上采用基于分数阶的梯度更新方法生成新的滤波算法,即FMCC算法.将代入(4)式,可得FMCC算法的代价函数,即

基于分数阶的梯度更新方法是在(5)式一阶微分的基础上增加一项分数阶微分[19].因此,基于代价函数(12)式,FMCC算法的权重更新公式可以表示为

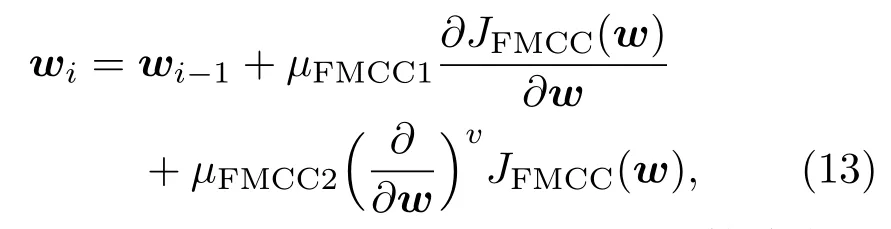
其中,µFMCC1和µFMCC2分别是FMCC算法中一阶微分和分数阶微分的学习步长.

类似于(5)式,(13)式中的一阶微分部分为

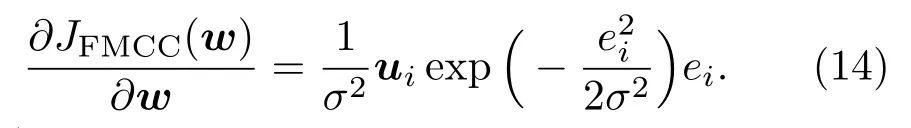
采用(10)式中定义的RL微分运算,结合(11)式可将(13)式中的分数阶微分更新部分表示为[19]

其中,⊙表示点积.

因为微分计算后的常系数可归结到步长系数中,所以在梯度更新中通常忽略该常系数.将(14)式和(15)式中等式右边的第一个常系数1/σ2分别归入到步长µFMCC1和µFMCC2中,代入(13)式可得FMCC算法的最终权重更新公式:

从(16)式可以看出,和传统的MCC算法相比,FMCC算法更灵活,有更多的调节参数.µFMCC2和v可以用不同的强度进一步缩放对权重向量更新的影响,因此,可以进一步提升收敛速度,降低预测误差.FMCC算法可以总结如下.

初始化参数的选择:µFMCC1,µFMCC2,v.

结合{ui,di}(i＞1)数据对按下列步骤计算:

步骤1计算实际输出:

步骤2计算预测误差:

步骤3更新权重向量:

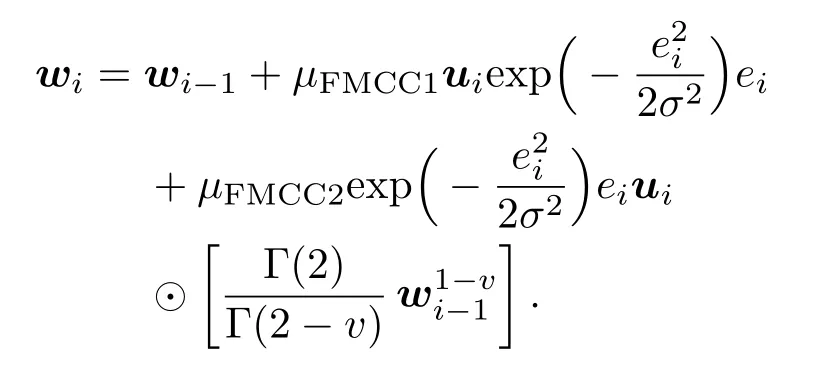
因此,从 FMCC算法的描述中,可以发现该算法具有以下特点:1)FMCC算法更新是基于最大相关熵准则,因此与基于MMSE准则的算法相比,借助最大相关熵准则的鲁棒性,FMCC算法可以有效抑制非高斯噪声的影响;2)与MCC算法相比,FMCC算法在权重更新时增加了分数阶微分部分,因此能够更好地找到最优解,在以增加一定计算复杂度的前提下提高预测精度.

4 仿 真

为了验证本文所提的FMCC算法的有效性,将FMCC算法用于混沌时间序列的预测.选用具有代表性的Mackey-Glass(MG)混沌时间序列[28]和Lorenz混沌时间序列[29]作为实例.本实验所用噪声是alpha噪声[30].对于所有的仿真,所用alpha噪声是稳定分布的,其参数设置为:特征指数a=1.3,分散系数γ=0.01,对称参数β=0和位置参数δ=0.为了评价滤波器的精度,定义均方误差(mean square error,MSE)为

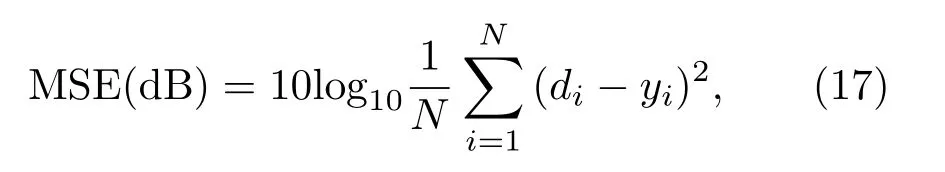
其中,di是滤波器的期望输出,yi是滤波器的实际输出,N=100是测试数据的个数.为了消除仿真中的随机性,本文取100次蒙特卡罗仿真实验的平均值来计算MSE.

为了全面地评价本文提出的FMCC算法的有效性和可靠性,选用LMS算法[9]、MCC算法[15]和分数阶最小均方(fractional-order least mean square,FLMS)算法[19]作为比较算法.其中,LMS算法和MCC算法分别是MMSE准则和MCC准则的代表算法,FLMS算法是分数阶算法的代表算法.

4.1 Mackey-Glass混沌时间序列的预测

自 Mackey和 Glass发现时滞系统中的混沌现象以来,时滞系统便引起人们的广泛关注,并常常被用为检验非线性系统模型性能的标准.MG混沌时间序列由以下时滞微分方程产生[28]

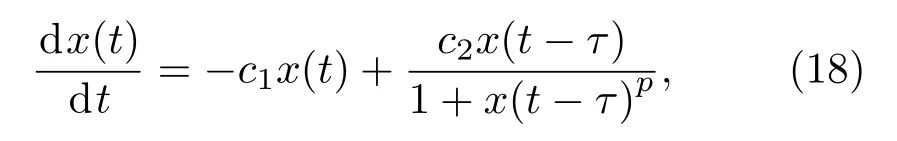
其中,c1=0.1,c2=0.2,p=10,τ为时滞参数.MG方程能够体现周期和混沌的动力学特性,已被用于各种生理系统的建模,如血液中电解质、葡萄糖、氧气在各种器官中的物理模型[28].当τ＞17时系统呈现混沌特性,且其τ值越大,混沌程度越高.本文所用时滞参数τ=30.该微分方程采用6 s的采样周期进行离散化得到混沌时间序列.选取该混沌时间序列稳态中的20000个数据点作为训练数据,后100个作为测试数据.图1是一段MG混沌时间序列及被噪声污染后的序列图.

仿真中,ui=[xi−7,xi−6,·,xi−1]T作为输入来预测当前时刻的期望值xi.首先,讨论分数阶阶数v对FMCC预测混沌时间序列性能的影响.图2显示了不同分数阶阶数v下FMCC预测MG混沌时间序列的均方误差曲线.由图2可知,当分数阶的阶数v取0.25时,算法的均方误差曲线达到最小.因此,在以下的仿真中,分数阶的阶数设置为0.25.

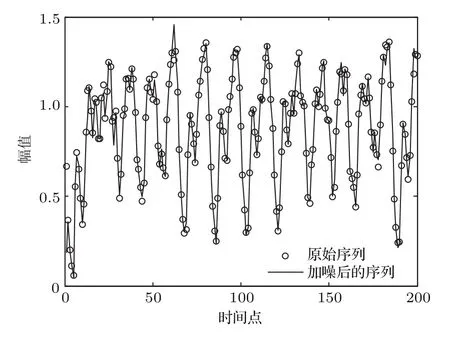
图1 MG混沌时间序列的一个部分Fig.1.Segment of the MG chaotic time series.

图2 不同分数阶下FMCC的均方误差Fig.2.MSEs of FMCC under different fractional orders.

表1 基于100次蒙特卡罗仿真的混沌时间序列预测性能比较Table 1.Performance comparison of chaotic time series predication over 100 Monte Carlo runs.

表1显示了不同算法在本例仿真中的均方误差和100次蒙特卡罗仿真消耗计算时间的结果.由表1可以看出,在MG混沌时间序列预测的结果中,FMCC的预测性能优于其他滤波器算法.和MCC和LMS这两种在权重更新的过程中仅仅具有一阶微分的算法相比,FMCC在增加一定计算时间的前提下,降低了混沌时间序列预测的稳态MSE,即FMCC以增加一定计算量为代价提高了对混沌时间序列的预测精度.

最后,图3显示了FMCC,MCC,LMS和FLMS算法对MG混沌时间序列预测的均方误差曲线,其中,LMS和MCC的步长参数均设置为µLMS=µMCC=0.002,FLMS和FMCC的两个步长分别设置为µFLMS1=µFMCC1=0.002和µFLMS2=µFMCC2=0.004,核参数设置为σ=0.6.从图3中可以看出,由于FLMS和LMS算法是基于MMSE准则,因此在alpha脉冲噪声的环境下性能有所下降.而FMCC和MCC算法是基于最大相关熵准则,因此具有较好的鲁棒性,能够对alpha噪声产生较好的抑制作用.在其他参数一致的情况下,FMCC算法对混沌时间序列的预测性能优于MCC.

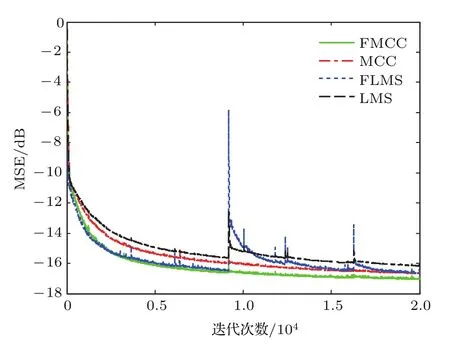
图3 在MG混沌时间序列预测时不同算法的MSE学习曲线Fig.3. Mean-square error curves of different algorithms in Mackey-Glass chaotic time series.

4.2 Lorenz混沌时间序列的预测

作为一个最经典的混沌模型,Lorenz系统的研究纵贯整个混沌科学的发展,几乎与所有混沌科学的重要发展都密切相关[31].因此Lorenz系统的研究对整个非线性科学的发展具有重要的意义.

Lorenz系统[29]可由三元一阶常微分方程组表示为:

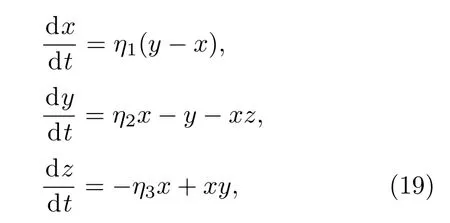
其中,η1=16,η3=4,η2=45.92. 利用步长为0.01的四阶Runge-Kutta方法求解方程(19)的数值解.在第1001到18000个数据集中选取前8000个作为训练数据,后100个数据点作为计算MSE的测试数据.类似于实例一,首先,讨论分数阶对FMCC预测性能的影响.图4显示了不同分数阶阶数v下FMCC对Lorenz混沌时间序列预测的均方误差曲线.由图4可知,当分数阶阶数v=0.5时,FMCC算法对Lorenz混沌时间序列预测的稳态误差最小,因此,在以下的仿真中,分数阶的阶数v=0.5.

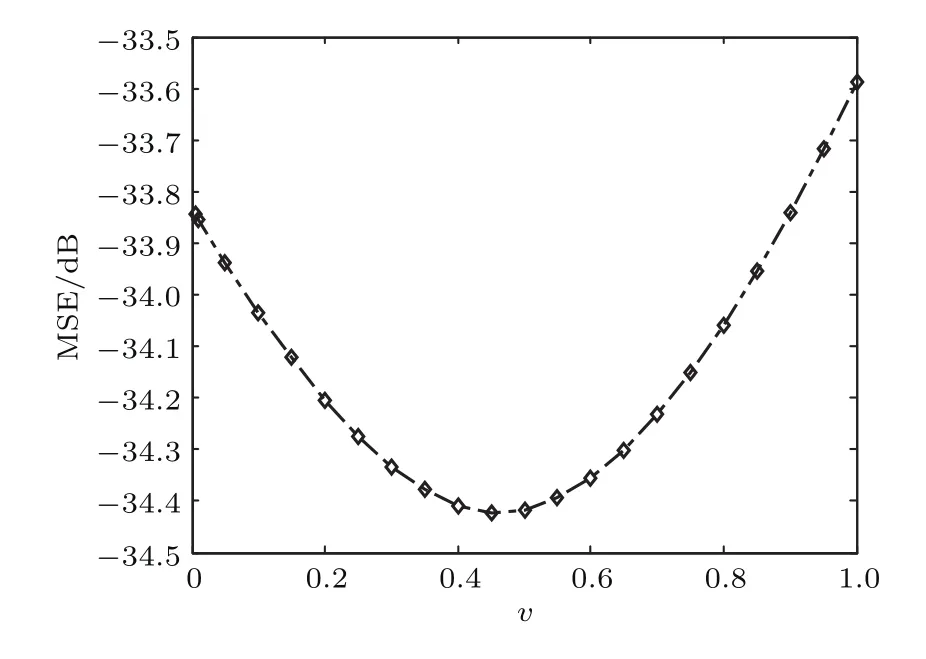
图4 不同分数阶下FMCC的均方误差Fig.4.MSEs of FMCC under different fractional orders.

图5 在 Lorenz混沌时间序列预测时不同算法的MSE学习曲线Fig.5. Mean-square error curves of different algorithms in Lorenz chaotic time series.

图5显示了FMCC,MCC,FLMS和LMS在alpha噪声环境中预测Lorenz混沌时间序列时的均方误差曲线. 此时训练数据的个数是8000,算法参数配置为:LMS和MCC的步长均设置为µLMS=µMCC=0.006,FLMS和FMCC的两个步长分别设置为µFLMS1=µFMCC1=0.006和µFLMS2=µFMCC2=0.006,核参数设置为σ=0.7.从图5可以看出,与其他滤波算法相比,FMCC算法对Lorenz混沌时间序列的预测速度最快,稳态误差最小.由于系统所加噪声是非高斯噪声,FLMS算法和LMS算法在非高斯噪声环境中性能均较差.综合以上两种混沌时间序列的仿真结果可以看出,本文提出的FMCC在非高斯环境下对混沌时间序列的预测具有较好的鲁棒性和预测精度.由于Lorenz和MG序列是具有代表性的混沌时间序列,因此FMCC算法可有效地拓展到其他混沌时间序列的预测.

5 结 论

本文利用分数阶微分改进了MCC算法的权重更新方式,进而提出了一种用于混沌时间序列预测的FMCC算法.在增加一定计算复杂度的前提下,通过选择合适的分数阶阶数v,FMCC算法能够提高对混沌时间序列的预测精度.作为算法中的关键参数,分数阶的阶数与预测精度之间的关系呈非线性,且与所处理的实际非线性物理系统相关.因此,针对不同的非线性系统,为达到最优的预测精度可通过仿真实验事先选定合适的分数阶的阶数.仿真结果表明:与基于MMSE准则的LMS和FLMS算法相比,FMCC算法因采用最大相关熵准则,所以对非高斯噪声具有较好的抑制作用和鲁棒性,能够在alpha噪声中取得理想的预测结果;与MCC算法相比,FMCC算法因在传统梯度更新方法中增加了分数阶微分部分,能有效地提高预测精度.因此,FMCC算法可提高混沌时间序列的预测速度和预测精度,为混沌时间序列预测提供了一条有效的途径.

[1]Tang Z J,Ren F,Peng T,Wang W B 2014Acta Phys.Sin.63 050505(in Chinese)[唐舟进,任峰,彭涛,王文博2014物理学报63 050505]

[2]Song T,Li H 2012Acta Phys.Sin.61 080506(in Chinese)[宋彤,李菡 2012物理学报 61 080506]

[3]Zhang J S,Xiao X C 2000Chin.Phys.Lett.17 88

[4]Farmer J D,Sidorowich J J 1987Phys.Rev.Lett.59 845

[5]Zheng Y F,Wang S Y,Feng J C,Tse C K 2016Digit.Signal Process.48 130

[6]Meng Q F,Zhang Q,Mou W Y 2006Acta Phys.Sin.55 1666(in Chinese)[孟庆芳,张强,牟文英 2006物理学报55 1666]

[7]Takens F 1981Lecture Notes Math.898 366

[8]Al-saggaf U M,Moinuddin M,Arif M,Zerguine A 2015Signal Process.111 50

[9]Gui G,Peng W,Adachi F 2014Int.J.Commun.Syst.27 2956

[10]Ozeki K,Umeda T 1984Electr.Commun.Jpn.67 19

[11]Van V S,Lazarogredilla M,Santamaria I 2012IEEE Trans.Neural Netw.Learn.Syst.23 1313

[12]Qiao B Q,Liu S M,Zeng H D,Li X,Dai B Z 2017Sci.China:Phys.Mech.60 040521

[13]Erdogmus D,Principe J C 2002IEEE Trans.Neural Netw.13 1035

[14]Hu T,Wu Q,Zhou D X 2016IEEE Trans.Signal Process64 6571

[15]Chen B D,Xing L,Liang J L,Zheng N N,Principe J C 2014Signal Process.Lett.21 880

[16]Shi L M,Lin Y 2014Signal Process.Lett.21 1385

[17]Chen B D,Principe J C 2012IEEE Trans.Process.Lett.19 491

[18]Chen Y,Li S G,Liu H 2016Acta Phys.Sin.65 170501(in Chinese)[陈晔,李生刚,刘恒 2016物理学报 65 170501]

[19]Shah S M,Samar R,Khan N M,Raja M A Z 2016Nonlinear Dyn.88 839

[20]Zhou Y,Ionescu C,Machado J A T 2015Nonlinear Dyn.80 1661

[21]Shah S M,Samar R,Raja M A Z,Chambers J A 2014Electron.Lett.50 973

[22]Santamaria I,Pokharel P P,Principe J C 2006IEEE Trans.Signal Process.54 2187

[23]Liu W,Pokharel P P,Principe J C 2007IEEE Trans.Signal Process.55 5286

[24]Aronszajn A 1950IEEE Trans.Am.Math.Soc.68 337

[25]Duan J W,Ding X,Liu T 2017Sci.China:Inf.Sci.60 1

[26]Huang S,Zhang R,Chen D 2016J.Computat.Nonlinear Dyn.11 031007

[27]Shoaib B,Qureshi I M 2014Chin.Phys.B23 050503

[28]Mackey M C,Glass L 1977Science197 87

[29]Lorenz E N 1963J.Atmos.Sci.20 130

[30]Li B B,Ma H S,Liu M Q 2014J.Electron.Inf.Technol.36 868(in Chinese)[李兵兵,马洪帅,刘明骞2014电子与信息学报36 868]

[31]Stewart I 2000Nature406 948