多维温度场对光纤环Shupe效应误差影响的理论分析∗

2018-03-19卓超杜建邦

物理学报 2018年1期

卓超杜建邦

(北京航天自动控制研究所,宇航智能控制技术国家级重点实验室,北京 100854)

1 引言

光纤陀螺是利用多层光纤环中沿正反方向传播光束的相位差来检测相对惯性空间的转动[1].作为惯性导航系统的核心仪表,光纤陀螺测量精度目前已达到战略级水平,引领了惯性技术的发展方向[2].然而,光纤环易与使用环境中多种物理量[3−6](湿度,电磁,气压,温度)相互作用而导致精度下降的特点已成为制约其性能进一步提高的瓶颈问题.因此,将环境变量对于光纤环的作用机理进行建模与分析有助于定位关键误差源并降低相关因素的影响.

在诸多影响因素中,温度效应作为影响光纤环性能的首要因素受到研究者的广泛重视.Shupe[7]首先阐释了瞬态温度变化会引起光纤折射率改变并导致非互异性相移,从而造成陀螺零偏漂移的产生.其中一个重要推论是如果能严格保持温变分布关于光纤长度中点的对称性,就可以消除Shupe效应误差.基于此,研究人员提出了以四极绕法为代表的多种光纤环绕制方法[8−10]并分析了瞬态温度场对于不同绕线方式下陀螺零偏漂移的影响模式[11−14].文献[15]推导了沿光纤环径向传播的热传导模型,并与漂移相结合,揭示了热源分别位于陀螺内外部时引起不同零偏响应的本质原因.文献[16]则进一步考虑了四极绕法光纤环在径向温度梯度作用下非等长绕线误差并给出了非对称长度的辨识方法.从公开发表文献来看,目前多数研究工作都是在只有径向温度变化的假设下开展,很少关注多维温度场的情况,文献[17]仅半定量讨论了轴向温变速率的影响.这对于Shupe效应误差机理的描述不够完善,且很难适用于实际复杂的工作温度条件.本文系统地推导了沿径向、轴向与圆周方向温度场引起四极绕法光纤陀螺零偏漂移的表达式,并分析了热源空间分布对于温度效应误差的影响,为导航仪表及系统的热设计与结构优化提供了理论基础与工程指导.

2 Shupe效应误差理论分析

2.1 光纤环零偏误差模型

温度变化会引起光纤环中沿正反方向传播的两束光产生附加相移而造成零偏漂移误差ΩE,其表达式[15]为

式中,L为光纤长度;T表示温度;˙T为温度的时间导数,即温变速率;n为光纤折射率;∂n/∂T为折射率温度系数;D为光纤环平均直径.令

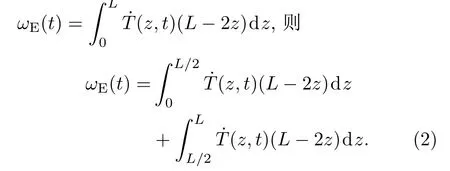
对等式右边第二项做变量替换,令x=L−z,变换后将x再替换回z,有

(3)式适用于不同绕制类型的光纤环,以下就四极绕法这一典型绕制形式展开针对性推导.

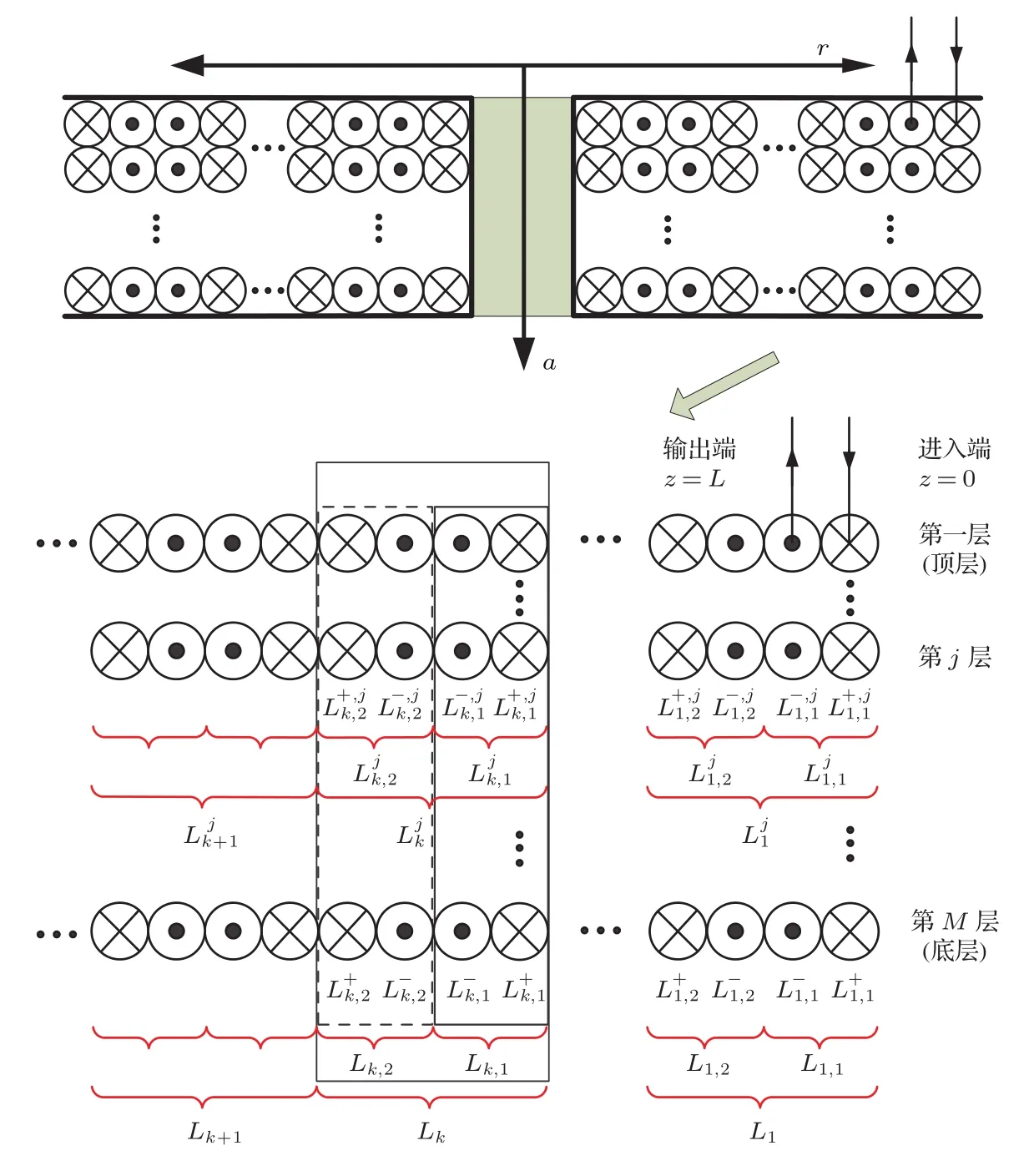
图1 四极绕法侧视剖面图Fig.1.Cross section of the quadrupole winding design.

四极绕法侧视剖面示意图见图1.设光纤环沿轴向a的层数为M,所包含的四极单元(图中细实线框内的部分称为一个四极单元)总数为N,故沿径向r的光纤环总数为4N.将(1)式中积分限的下限z=0定义为光纤进入端,它同时也是环中沿某方向传播光线的起点,这里不妨设为从径向最外环光纤开始;相邻倒数第二环的终点则作为上限z=L,记为输出端.相应靠近光纤进出端的第一层称为顶层,第M层则为底层.×状圆圈表示z＜L/2部分的光纤,而点状圆圈表示z＞L/2部分的光纤,由于两部分光纤紧密排列,使得温度效应能够相互抵消[18].由光纤进入端自外径向内径方向第k个四极单元所包含的光纤集合记为Lk(细实线方框内),再将Lk分为两部分Lk,1与Lk,2.Lk,1为Lk中z＜L/2部分光纤相比z＞L/2部分光纤更靠近外径的光纤集合(粗实线方框内);Lk,2则正好相反(虚线方框内).最后将Lk,1与Lk,2中z＜L/2的光纤与z＞L/2的光纤再分别用上标“+”、“−”加以区分. 另一上标“j”则表示针对第j层的相应部分.

根据上述记法约定,ωE(t)可表示为

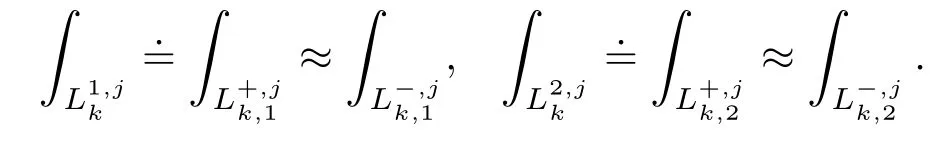
于是将(4)式改写为

2.2 径向与轴向温度场情况

当温变速率˙T只是光纤环径向距离r和轴向距离a的函数时,由于是线积分,在(5)式中做变量代换,得

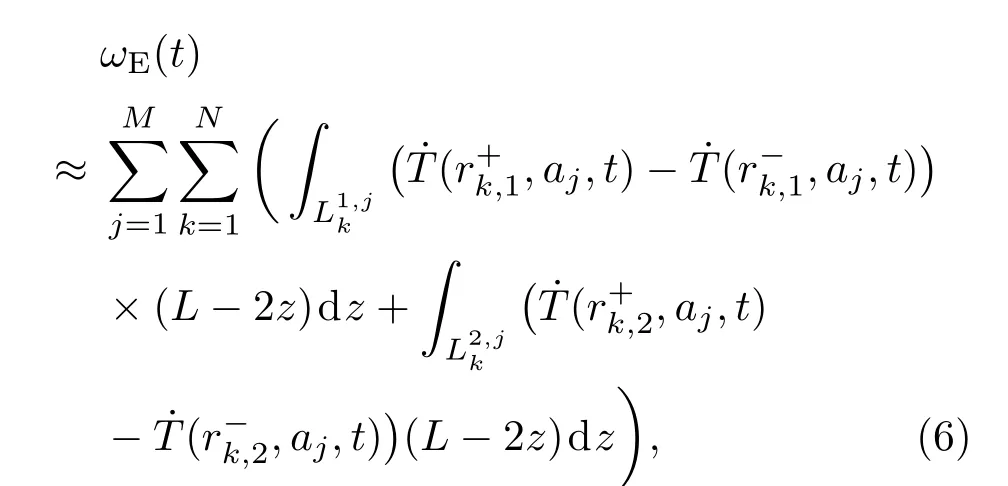
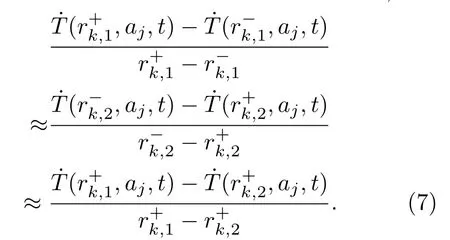
将(7)式代入(6)式,提出与积分无关的温度变量,有

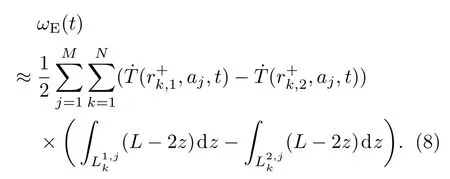
如果不考虑由于半径变化所引起的各四极单元光纤环长度变化,可以证明:

对j=1,2,···,M成立,同时S1＞S2＞···＞SM＞0.

综合(8)和(9)式得到

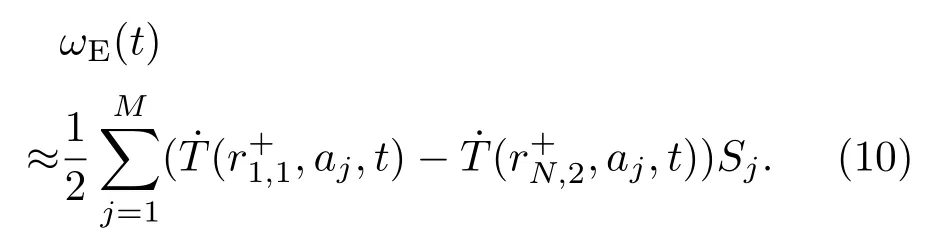
可以看到,当光纤环只受到径向与轴向的瞬态温变作用时,温度引起的四极绕法零偏误差是光纤环各层外内壁温度时间导数之差的加权和,并且越靠近光纤进出的顶层,其所占份额越大,且这种增大呈线性.顶层加权系数S1近似为底层SM的2M倍.(10)式的符号由起始点位置确定,若以最外环相邻的倒数第二环起始点作为光纤进入端,则需要反号,零偏误差将为各层内外壁温变速率之差的加权和.

当温度变化率只与径向r有关时,对任意j,有(10)式可化简为

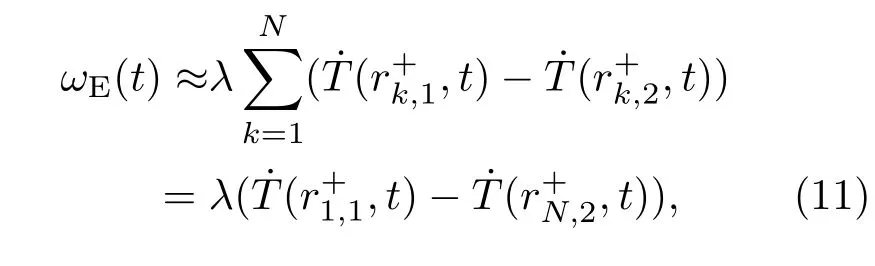
式中,λ=(L/4N)2.此时,Shupe效应误差只与光纤环外内壁的温度时间导数差值成正比.

2.3 圆周方向温度场情况

进一步分析当圆周方向存在温度变化时,Shupe效应误差对零偏漂移的影响.四极绕线方式的俯视示意图见图2.其中,图2(a)表示N个四极单元所组成的光纤环.定义光纤环中沿顺时针方向传播的光线起点为光纤进入端(最外环光纤起始端),图中箭头表示光的传播方向.与侧视图1相同,×状圆圈表示z＜L/2部分的光纤,而点状圆圈表示z＞L/2部分光纤.P表示光纤长度的中点,即z=L/2的位置.光纤进出端与长度中点的连线称为对称中心线S(点划线表示).S与靠近进出端的交线记为SR,称作近端交线;另一侧交线记为SF,称作远端交线.图2(b)将N个四极单元简化为一个,用于说明四极绕制方式.它其实是将中点P固定于骨架上,z＜L/2部分的光纤(粗实线表示)绕骨架逆时针缠绕,而z＞L/2部分的光纤(虚线表示)则顺时针缠绕.这里的箭头表示绕制的方向.四极绕线方式将造成光线传播距离z(z＜L/2)与L−z(相距光纤输出端距离为z)关于中心线S两侧对称.

此时如果温度变化在圆周方向(φ方向)也存在空间不均匀性,适用于径向与轴向的(10)式在此情况下不能成立.原因是由于对称线两侧等距离位置z与L−z在多数情况下相距较远,无法形成径向方向上的紧密相邻,故(6)和(7)式不成立.这里利用(5)式,以

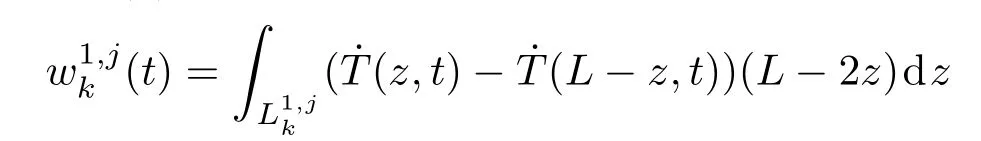
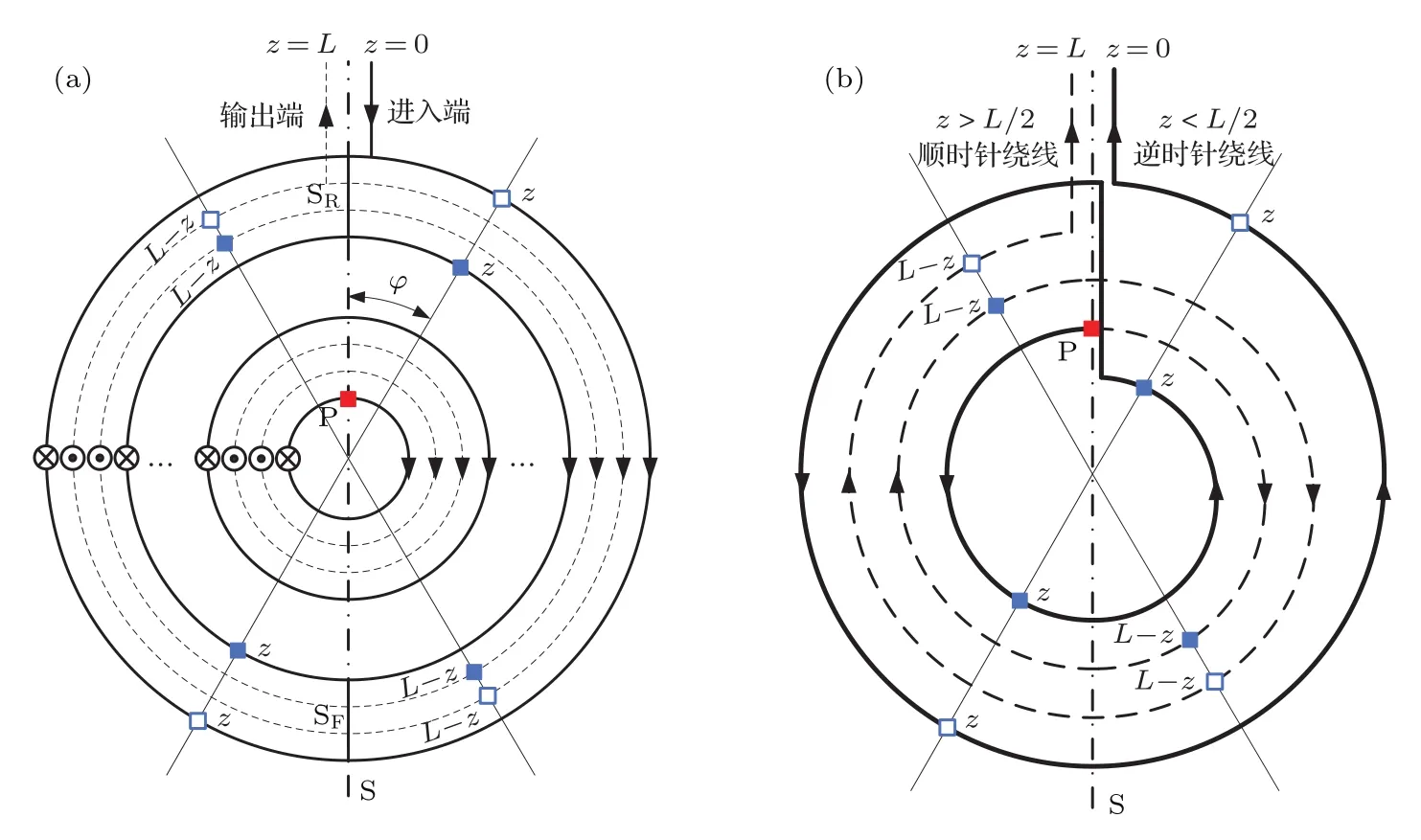
图2 四极绕法俯视图 (a)四极单元示意图;(b)绕线方式示意图Fig.2.Top view of the quadrupole winding:(a)Schematics of quadrupole sets;(b)schematics of the coiling pattern.

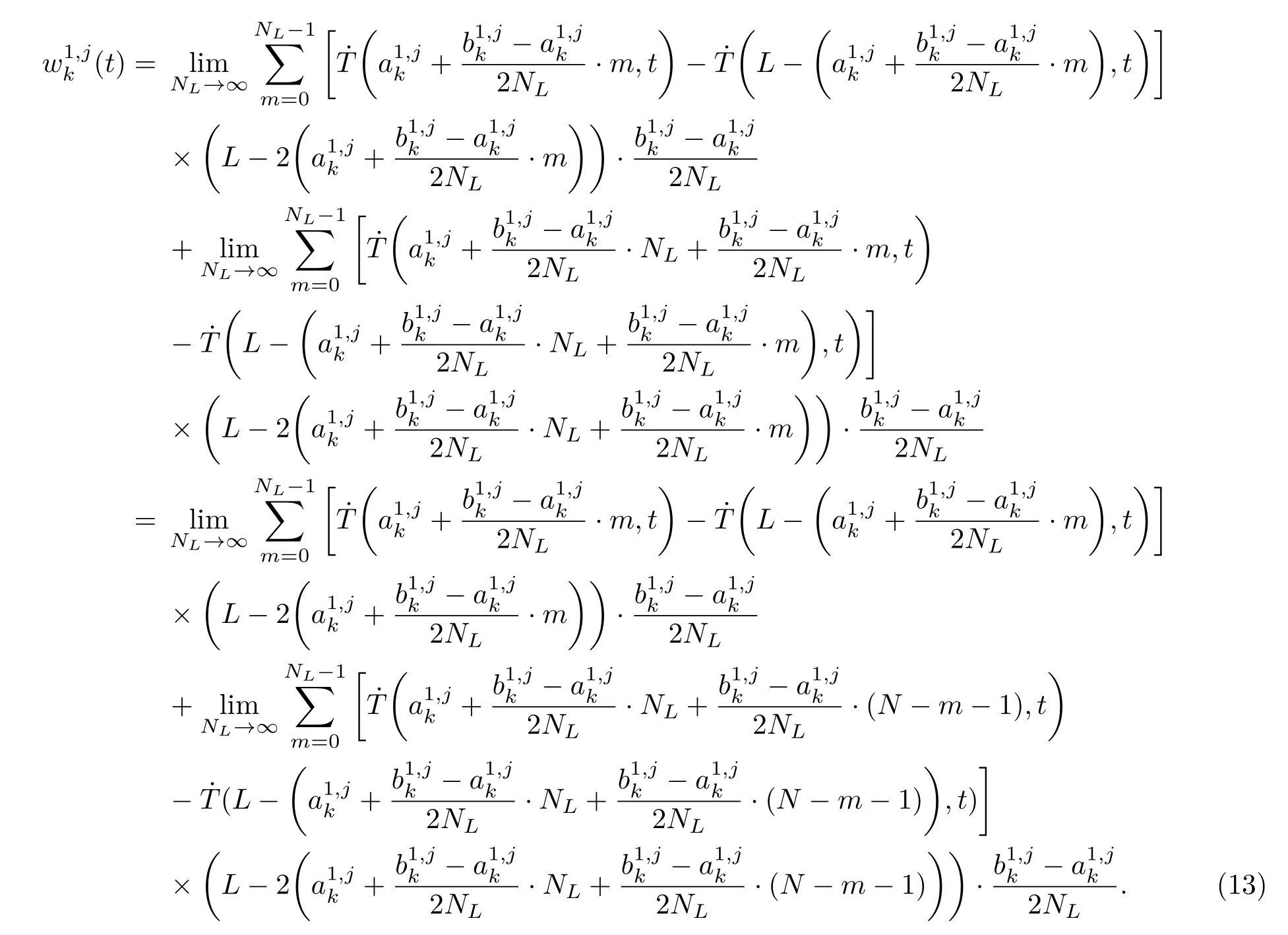
由图2(a)可见,除靠近交线SR与SF的少部分区域,存在如下近似:

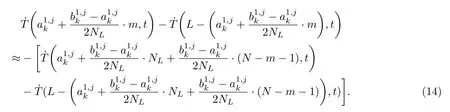
将(14)式代入(13)式,得到

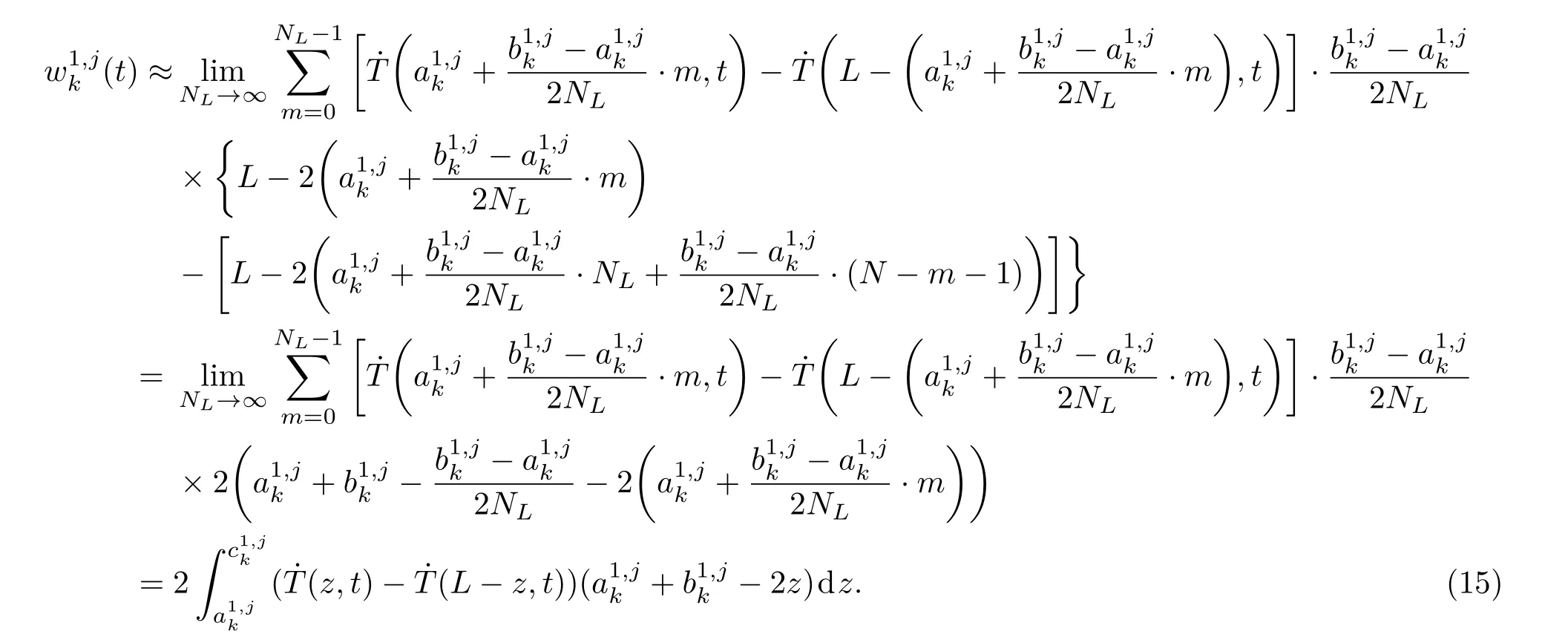
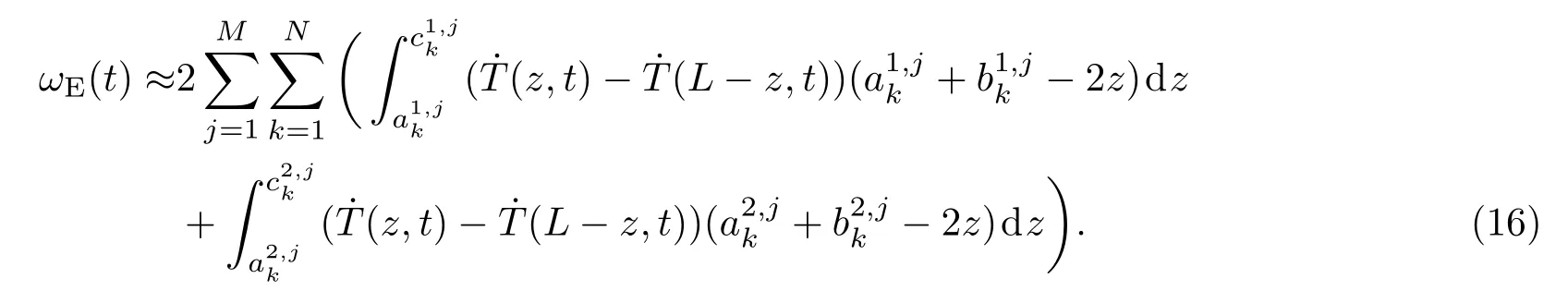
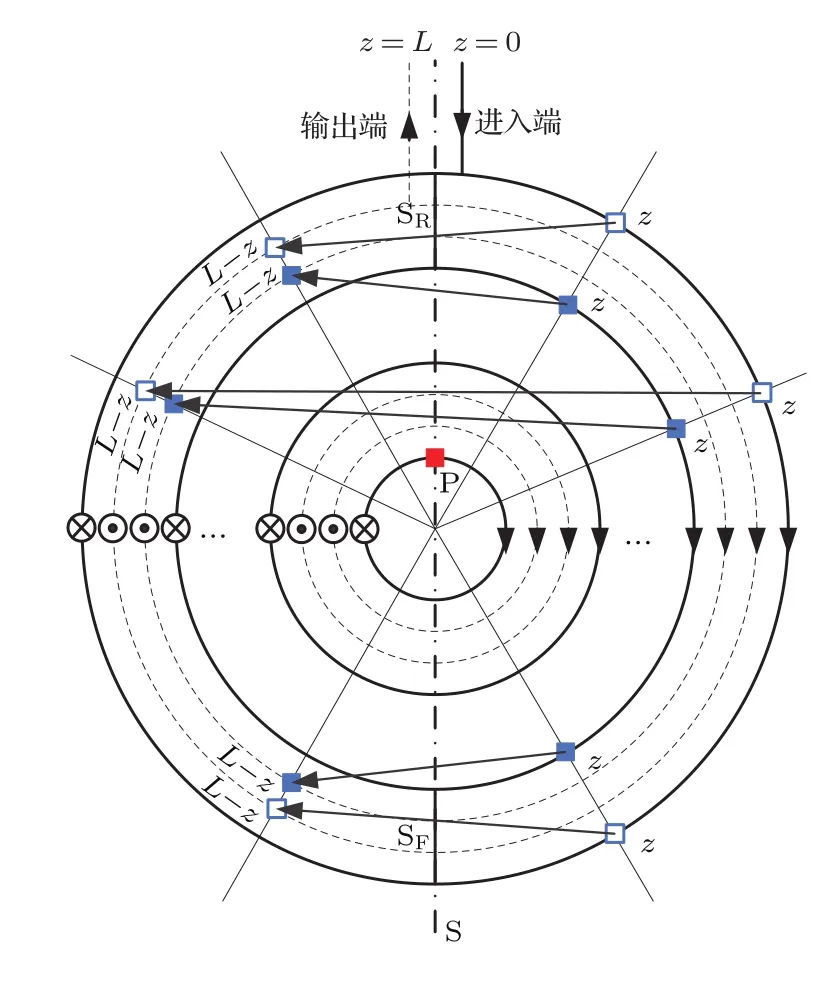
图3 对称中心线两侧温变分布对于零偏误差的影响Fig.3.In fl uence of the thermal distribution in both sides of the symmetric centerline on the bias error.

上述公式的物理意义如图3所示,误差输出是每一组四极单元中位于线S两侧对称位置z(z＜L/2)与L−z处温变速率空间差值的加权和,图中箭头表示两位置温变速率作差.加权系数为0,i=1,2. 对任意i,j,加权系数为z的线性减函数,其上界为一匝线圈的长度,下界为零.可以看到,图中总是右半平面“+”部分光纤(z＜L/2)的温变速率减去左半平面对称位置“−”部分(z＞L/2)的温变速率,因而当不存在径向与轴向温度梯度时,圆周方向的温度不均匀仍然会产生Shupe效应误差.但如果此时不均匀关于中心线对称,则可以消除由于周向温度梯度引起的漂移误差.当径向、轴向和圆周方向的空间温度梯度耦合在一起时,由于光纤环圆周方向相比于轴向和径向跨越了更大的空间尺度,因而更易引起较大的温度不均匀,且这部分误差并不能够像径向误差一样被四极绕法所抵消,故可能成为零偏漂移的主要因素.因而利用结构设计和材料选取保证温度分布关于线S的对称性,将有助于减小Shupe效应误差的产生.

3 数值仿真与分析

鉴于空间温度场的解析求解相对困难,这里采用有限元方法计算光纤环瞬态温度场,进而获得温变速率,并结合Shupe效应误差方程以模拟零偏漂移的变化情况.以某型光纤陀螺为参考,采用135型光纤,设置光纤环几何结构为内径97 mm,外径112 mm,高度12 mm,轴向层数M=89,径向环数4N=56.光纤环材料参数列于表1[11,15].

表1 光纤环材料参数Table 1.Material parameters of the fi ber coil.

3.1 热量沿径向与轴向传导时的仿真结果

在仿真沿光纤环径向与轴向传递的热量所引起的陀螺零偏误差时,为比较轴向温变梯度对于漂移的影响,分别设置光纤环内壁表面上半部分(其临近光纤进出端的顶层)与下半部分(临近底层)存在功率为1.5 W的均匀热源(图4(a),(c)中的深色所示),其余表面设置为绝热,光纤环初始温度为20°C.两种条件下,计算得到的温度场分布(t=100 s时)如图4(b),(d)所示;零偏误差随时间的变化对比如图5所示.

图4 热量沿径向与轴向传导时温度场仿真结果 (a),(b)热源位于内壁上半部时光纤环示意图及相应t=100 s时的温度分布图;(c),(d)与(a),(b)类似,但热源位于内壁下半部Fig.4.Simulation results of the thermal fi eld when the heat propagates along radial and axial directions:(a),(b)Representation of the fi ber coil when the heat source is located at the upper half of the inner side and the corresponding temperature distribution at t=100 s;(c),(d)same as(a),(b)with heat source located at lower half.

图5 热源分别位于光纤环内壁上下表面时零偏误差对比Fig.5.Comparison of bias errors with heat sources located at upper and lower surfaces of the ring’s inner side respectively.

图5中蓝色实线为热源位于内壁表面上半部时,陀螺漂移输出;红色虚线则为热源位于内壁表面下半部时相应结果.可以看到,当热源更靠近光纤进出端的顶层时,所引起的零偏漂移大于热源靠近底层的情形.因而应在设计及使用中避免光纤陀螺进出纤的顶面接近热源.

3.2 热量沿圆周方向传导时的仿真结果

为讨论圆周方向存在不均匀温度场的情况,光纤环初始温度同样设置为20°C,内外壁与上下表面采用绝热边界条件,再分两种情况设置沿顺时针方向与对称中心线S成φ角的光纤环横截面A1A2与B1B2的温度边界条件,参见图6.

1)设置单截面A1A2为50°C恒温边界条件,称作“单边条件”;

2)设置双截面A1A2与B1B2为50°C恒温边界条件,称作“双边条件”.

图6 圆周方向不均匀温度场下光纤环几何示意Fig.6.Geometry of the fi ber coil in the circumferentially nonuniform thermal fi eld.

如此设置是考虑到光纤环内外直径相差较小,通过改变横截面与线S的夹角φ,并取环中心温度代表周向温度,就可以近似模拟不同周向温度场在光纤环上的分布,仿真结果如图7和图8所示.

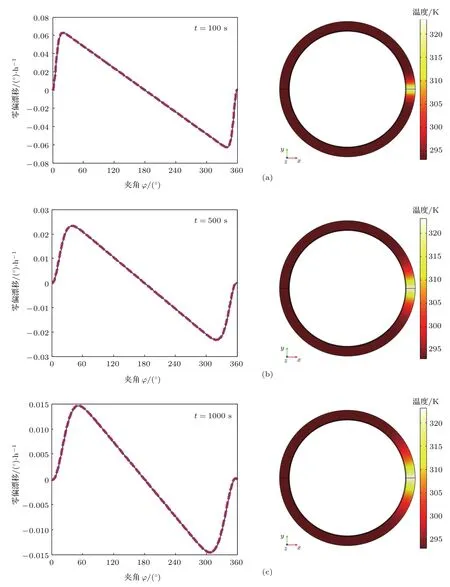
图7 (a),(b),(c)图示左边为单边条件下,t=100 s,500 s,1000 s时零偏误差随夹角φ的变化情况;右边为对应时刻φ=90◦时光纤环温度分布Fig.7.Left parts of(a),(b),(c)are bias errors as a function of angle φ at t=100 s,500 s,1000 s under single-sided condition;right parts are temperature distributions of the fi ber coil at corresponding time when φ =90◦.

图7中左边三幅图展示了“单边条件”下,对应t=100 s,500 s,1000 s时,陀螺零偏误差随夹角φ的变化规律,其中红色虚线与蓝色实线分别为利用原始(1)式与近似(16)式的计算结果,两者几乎重合,说明了推导公式的合理与正确性;右边三幅则为相应时刻,当φ=90°时,光纤环的温度分布.从左边三幅图中可以看到周向温变梯度引起了较大的漂移输出,并且误差曲线存在两个零点,分别对应φ=0°与φ=180°,这恰好为周向温度不均匀(横截面A1A2的位置)构成了关于线S的对称条件.

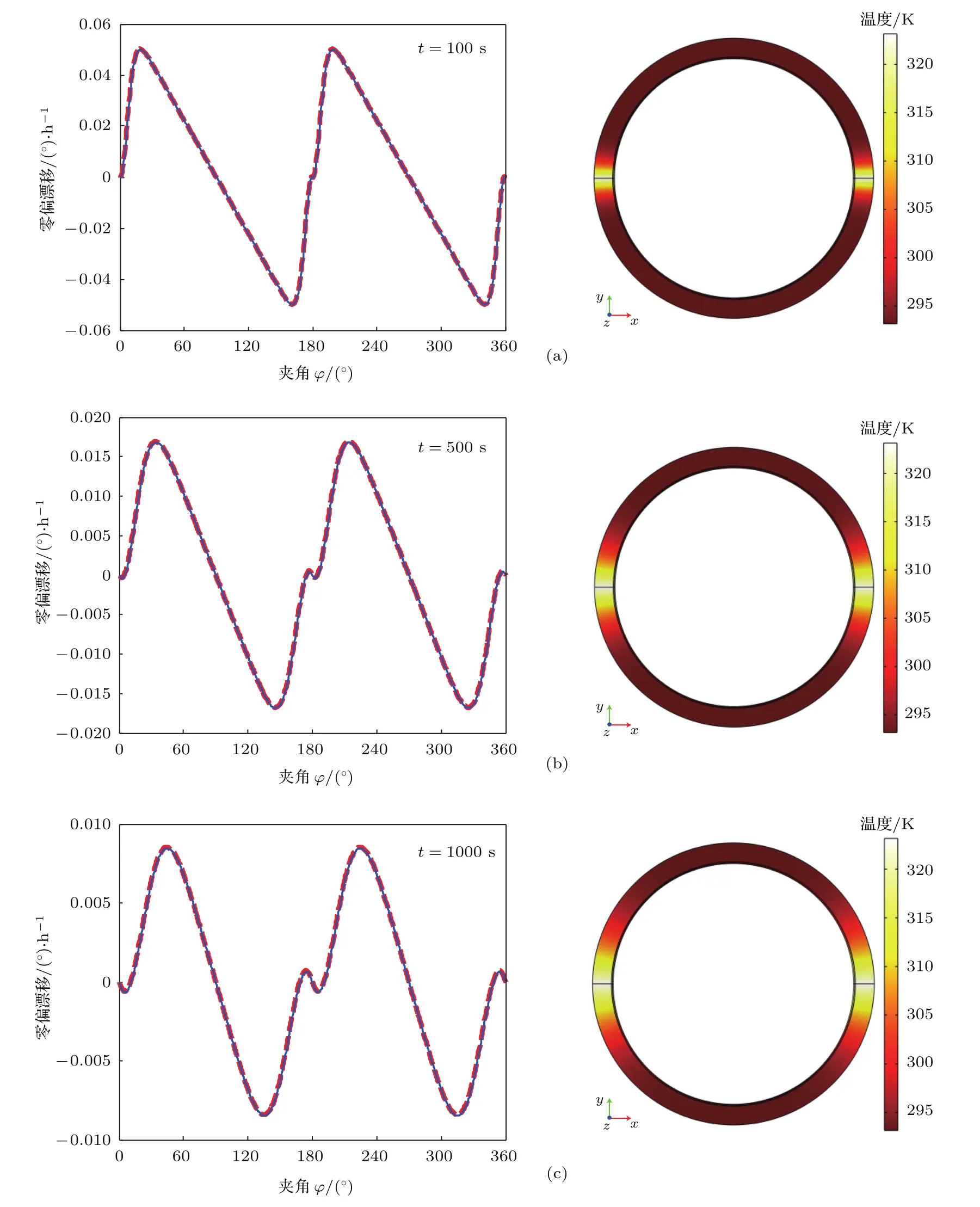
图8 (a),(b),(c)图示左边为双边条件下,t=100 s,500 s,1000 s时零偏误差随夹角φ的变化情况;右边为对应时刻φ=90◦时光纤环温度分布Fig.8.Left parts of(a),(b),(c)are bias errors as a function of angle φ at t=100 s,500 s,1000 s under dual-sided condition;right parts are temperature distributions of the fi ber coil at corresponding time when φ =90◦.

当φ＜180°时,误差输出为正,这是由于正向温度不均匀位于S右半平面,因而0,结合非负的加权系数使得积分(16)式为正.当φ ＞180°时,相应因而输出为负.还可以观察到:当φ＜180°时,误差输出经历了快速增大,再缓慢下降的过程;φ＞180°时,情况则正好相反.同时随着时间延长,光纤环温度逐渐升高,温变的不均匀区域相应扩大,极值点出现的位置偏离光纤进出端的角度增大,但两个极值点都大约出现在温度不均匀全部离开近端交线SR的位置.上述现象是因为随着横截面A1A2顺时针旋转,从φ=0°的位置偏离光纤进出端,将破坏左右平面的对称性,使得快速增大,当不均匀基本移出SR时,误差输出将达到最大值,此后加权项开始起到主导作用,随着角度φ的继续增大,加权项的线性减小将造成输出误差的线性减小.当φ＞180°时则经历了相反的过程.因此,在光纤陀螺的热设计中应尽量保证周向温度不均匀关于中心线对称,同时还应让不均匀的位置尽量远离光纤进出端而分布在靠近远端交线SF的位置.这样不但能够减小误差输出,还有助于降低漂移随角度φ变化的敏感性.

图8为“双边条件”下的仿真结果.类比于单边情况,圆周方向瞬态温度分布在φ=0°,φ=90°,φ=180°和φ=270°存在四个位置关于线S对称,故在相应夹角处陀螺漂移输出存在四个零点.当φ偏离0°与180°时,零偏漂移的绝对值将迅速增大,这是由于在这两个位置,都存在一个温度不均匀(截面A1A2或B1B2)位于光纤进出端附近.而在φ=90°和φ=270°时,主要的不均匀位置都等距分布在距离进出端±90°处,而相距其较远.

进一步考虑径向与周向温度梯度耦合的情形,这也更接近于实际的工作环境.为减小计算量,不考虑轴向温变的影响.在光纤环内壁对应环心O的圆心角为30°范围内放置热源,相应功率设为0.5 W.光纤环初始温度为20°C,其余表面为绝热边界.陀螺零偏误差随夹角φ的变化及t=100 s时,对应温度分布如图9所示.可以看到,即使存在径向与周向耦合,由于圆周方向的温度不均匀相比径向跨越了更大的空间尺度而起到主导作用,故误差输出结果与上述单边条件相类似.

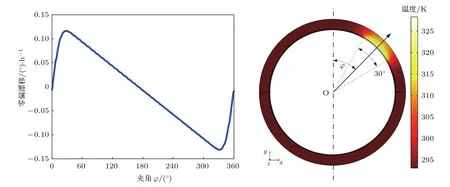
图9 径向与周向温度梯度耦合条件下,零偏误差随夹角φ的变化(左)及t=100 s,φ=45◦时相应温度分布(右)Fig.9.Bias error versus angle φ with the coupling of thermal gradients in radial and circumferential directions(left)and temperature distribution at t=100 s,when φ =45◦ (right).

4 结论

通过本文的理论分析与仿真验证,得到多维温度场对光纤环Shupe效应影响的主要结论如下.

1)当只存在沿径向与轴向的环境温变作用时,零偏误差正比于光纤环各层外内壁温度时间导数之差的加权和,并且所占份额将随着其接近光纤进出的顶层而线性增大.仿真结果表明热源位于光纤环内壁上表面时所引起零偏误差最大值是热源位于下表面的3倍.因此应尽量避免热源靠近进出光纤的陀螺顶面区域.

2)当圆周方向的温变空间分布关于光纤进出端与长度中点连线对称时,可以消除其所引起的漂移误差.同时应尽量使温度不均匀的位置远离光纤进出端而分布在远端交线附近,这将有助于减小漂移的产生并降低随角度变化的敏感性.

对于实际光纤惯导系统结构设计而言,可以首先通过整机的热仿真预先确定光纤环上温度梯度的产生位置,之后利用其结构上的旋转对称性,调整安装指向或直接改变光纤进出端的位置,使得进出端远离温度不均匀区域,并结合温度场优化设计使其尽量关于中心线成对称分布.当需要对光纤陀螺的温度漂移进行建模补偿时,为了更好地获得输出信号与温度的相关性,测温点的布置可以重点关注进出光纤的顶层与靠近光纤进出端的附近区域.

[1]Vali V,Shorthill R W 1976Appl.Opt.15 1099

[2]Paturel Y,Honthaas J,Lefevre H,Napolitano F 2014Gyroscopy and Navigation5 1

[3]Webber M,Willig R,Raczkowski H,Dineen A 2012J.Lightwave Technol.30 2356

[4]Wen F,Wu B J,Li Z,Li S B 2013Acta Phys.Sin.62 130701(in Chinese)[文峰,武保剑,李智,李述标 2013物理学报62 130701]

[5]Jin J,Li Y,Zhang Z C,Wu C X,Song N F 2016Chin.Phys.B25 084213

[6]Lü X Q,Huang X Y,Gao F,Wang X F 2015J.Chin.Inertial Technol.23 399(in Chinese)[闾晓琴,黄鑫岩,高峰,王学锋2015中国惯性技术学报23 399]

[7]Shupe D M 1980Appl.Opt.19 654

[8]Frigo N J 1983Proc.SPIE412 268

[9]Dyott R B 1996Electron.Lett.32 2177

[10]Williams M R 2008US Patent2008/0130010

[11]Tirat O F J,Euverte J M 1996Proc.SPIE2837 230

[12]Zhang C X,Du S S,Jin J,Zhang Z G 2011Optik122 20