利用思维导图优化高三学生数学各种题型的解题方法

曹颖慧

（保定市第二中学，河北 保定）

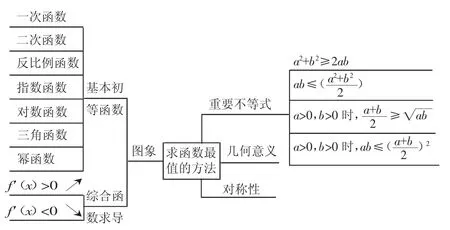
2017年我校申请的保定市教育科学“十三五”规划课题：《利用思维导图优化高三学生数学知识体系的研究》开展优化高三学生数学知识体系的实验研究，是在具有一定知识储备的基础上，寻求知识体系的表达方式、探索知识形象化、可视化工具的过程。有助于学生从整体上把握知识概要，局部上内化理解知识点，形成旧知与新情景的链接能力，有效避免了对知识的机械性记忆，实现了知识体系之间的贯通理解和转换。高三的学生已经有高一和高二的基础知识，在高三可以从两方面利用思维导图优化学生的思维体系，第一方面：将高中数学各章节知识进行优化；第二方面：将各种题型的解题方法进行优化。下面是以求函数的最值为例将各种题型的解题方法进行优化。

在高中求函数的最值通常有四种方法：一、知道函数的图象；二、用重要不等式；三、几何意义；四、对称性。

一、要知道函数的图象需要分析函数单调性

下面从两类函数出发以几个习题为例分析函数的最值。一类函数是基本初等函数，包括一次函数、二次函数、反比例函数、指数函数、对数函数、三角函数。另一类是综合函数需要用导函数分析函数的单调性。

（一）基本初等函数

1．将一条长为l的铁丝截成两段，分别弯成两个正方形，要使两个正方形的面积和最小，两段铁丝的长度分别是多少？

分析：设一段长度为x，则另一段长度为l－x，能推导出两个正方形的面积和为是一个二次函数。由二次函数图象可知（fx）在上单调递增，在上单调递减，所以 （fx）在处取最小值

2．已知函数 （fx）＝cos4x－2sinxcosx－sin4x。当时，求（fx）的最小值以及取得最小值时的集合。

3．在平面四边形 ABCD 中，AB⊥BC，AD⊥DC，∠BAD＝120°，AB＝AD＝1。若点 E 为边 CD 上的点，则的最小值是______。

分析：连接AC，由初中三角形知识容易得到BC＝DC且AC⊥BD。分别以DB、AC为x轴、y轴建立直角坐标系，设点E坐标为（x，y），点 A、B、C、D 的坐标分别为由E在CD上可得经计算得是关于x的一元二次函数，求最小值方法同例题1。

（二）综合函数

1．一边长为a的正方形铁片，从铁片的四角截去四个边长为x的小正方形，然后做成一个无盖的方盒。x多大时，方盒的容积V最大？

分析：这是含有指数函数类型的综合函数，需要用导数知识求函数的单调性。由导数知识得（fx）在上单调递减，在上单调递减，所以函数的最大值是

3．已知函数（fx）＝excosx－x。求函数（fx）在区间上的最大值和最小值。

分析：这是指数函数和三角函数的综合试题，由函数的导数可知函数上单调递减，∴函数（fx）在区间上的最大值是最小值是（f0）。这道题的特殊性在于需要对（fx）的导函数再求导分析导函数的单调性。

如果知道函数的图象就能求函数的最值，导数是很好的分析单调性的工具，知道了函数的单调性就能知道函数的图象。

二、下面以几个习题为例分析用重要不等式求最值

2．在△ABC 中，角 A、B、C 的对边分别为 a、b、c，已知 2（tanA＋

（Ⅰ）证明：a＋b＝2c；

（Ⅱ）求cosC的最小值。

分析：第（Ⅱ）问也是二元函数求最值问题。由第（Ⅰ）问知道代入余弦定理得利用不等式：a2＋b2≥2ab，得得到cosC的最小值为当且仅当△ABC为等边三角形时，cosC取最小值。

3．已知数列{an}满足 a1＝33，an+1－an＝2n，则的最小值是____。

注意：在用重要不等式求函数最值时需要注意条件，检查最值能否取到。

三、下面以几个习题为例分析用几何意义求最值

1．直线 l：x＋y＋2＝0 分别与 x轴、y 轴交于 A、B 两点，点 P 在圆C：（x－2）2＋y2＝2 上，则△ABP 的面积的最大值和最小值分别是？

分析：直线l与圆C相离，AB长为定值，△ABP的面积的大小取决于点P与直线l的距离，由几何意义可知过点P作直线l的垂线，垂线与圆交于两点，一点与直线l最远，一点与直线l最近。

四、下面以几个习题为例分析用对称性求最值

1．已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值是________。

分析：设正方体的八个顶点为ABCD—A1B1C1D1，平面α与AB、AD、AA1所成的角都相等，那么AC1⊥平面α。在平面α从点A向点C1移动的过程中，截面的形状是由三角形变成六边形再变成三角形，两边的情况是对称的，所以面积是先大再小。这样平面α过AC1的中点时面积最大，此时截面是边长为的正六边形。

注意：不到万不得已不用这个方法，毕竟这只是猜测，没有量化。

求最值可能出现在很多章节中，如函数、三角函数、数列、平面向量、立体几何、解析几何、概率统计等。不管出现在哪里，我们都要抽丝剥茧得到以核心变量为自变量的函数，再用上面的方法求最值。为了便于记忆，我把这些方法做成了思维导图，教学生用思维导图将求最值问题综合在一起，让学生能够掌握知识、掌握解题方法、培养思维习惯、感悟数学思想，形成一个知识体系。