基于速率-状态摩擦准则断层滑动失稳的数值模拟研究

王 威，陈在铁

（1.扬州市职业大学，江苏 扬州 225009；2.沙洲职业工学院，江苏 张家港 215600）

据统计，世界上大约90%的天然地震属于构造地震，构造地震具有震源深度浅、破坏严重的特点。大多数构造地震成因都是地壳板块滑动失稳后在断裂带释放出巨大能量，给人民的生命、财产造成了巨大的损失。因此，探索活动断层的滑动失稳性质具有重大意义，能够为防震、抗震提供正确的决策，减少人民的生命、财产损失。

当前的断层滑动失稳研究中，数值模拟已经成为一种重要方法[1-4]。但是对断层滑动模拟存在两个难点：一是断层自身的力学性质，断层滑动本质上是一种摩擦现象，传统的静∕动摩擦理论无法揭示断层滑动中出现的粘滑现象；二是断层模拟方法，断层本质上是岩体的不连续面，因此利用零厚度的Goodman单元或者是弱化单元都不能从根本上实现对断层的有效模拟[5]。本文基于FLAC有限差分程序，利用Fish语言在FLAC接触面单元中引入了速率-状态的摩擦准则，系统研究了断层活动速率对断层滑动失稳时产生的应力降及能量释放的影响规律，为进一步探索断层滑动失稳机制打下基础。

1 速率-状态摩擦准则

断层滑动的摩擦准则是模拟活动断层的关键之一。通过大量的岩石摩擦实验发现在滑动过程中，岩石摩擦存在弱化和愈合效应，Diterich和Ruina[6]经过大量的实验研究，提出了速率-状态摩擦准则：

式中：v为滑动速率；θ为状态变量；v*，μ*分别为参考速度及该速度下的稳态摩擦系数；A，B，L均为实验常数；μ为滑动速率为v时的摩擦系数。

由于直接应用速率-状态相关摩擦准则时，要解一个一阶微分方程组，对于数值模拟来说，这将会大大增加计算费用，甚至可能造成程序的不收敛，因此，如果要在数值模拟程序中引入速率状态相关的摩擦准则，必须对其进行数学处理。方程必须满足两个条件：初始条件和边界条件。初始条件为扰动速率突然变化的瞬间（即t=0时），摩擦系数产生一突变值，此时代表了方程的瞬时效应，稳态效应尚未发挥，即摩擦系数仅仅由A值产生影响，B值尚未来得及发生作用，故为初始条件；根据边界条件，当时间无穷大（即t→∞）时，摩擦将达到稳定状态，通过分离变量法可以得到状态变量为：

将（3）代入（1）中即可得到任意速率下的摩擦系数。

2 速率-状态摩擦准则在FLAC接触面单元的应用

2.1 FLAC接触面单元

快速拉格朗日连续介质分析（Fast Lagrangian Analysis of Continua）方法，简称FLAC，是由美国Itasca开发的应用于岩体力学计算的有限差分程序。

对于岩体不连续面FLAC中除了用节理化模型模拟节理岩体外，对于大型结构面如岩体中的节理、岩层的分界面、断层带等，FLAC还专门提供了界面接触单元来模拟。FLAC接触面的力学行为由界面节点的法向刚度（kn）、切向刚度（ks）、粘聚力（c）、摩擦角（φ）、剪胀角（ψ）和抗拉强度（σt）6个力学参数确定，每个节点的参数可以互不相同。接触面单元通过Mohr-Coulomb抗剪屈服准则和一个抗拉准则来描述接触面的变形、破坏状态。采用接触面单元，FLAC能够模拟接触面的挤压、滑动和张开等不同接触状态。接触面的抗剪强度准则为：

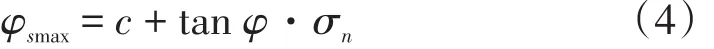
式中：c—粘聚力；φ—接触面的摩擦角；σn—法向应力。

2.2 速率-状态摩擦准则在FLAC中的应用

为了将速率-状态摩擦准则嵌入FLAC中，实现对断层滑动的模拟，在应用Flac进行数值模拟时，每一步加载通过fish语言读取接触面各点的应力、位移、速率等物理量，根据接触面的状态进行应力更新，直到加载结束。具体流程如图1所示。

图1 接触面分析流程图

3 活动断层运动性质的数值模拟分析

为研究活动断层滑动过程中，从应力积累到弹性释放再到强度恢复的全过程，这里采用远场边界速率的加载方式，在计算的过程中施加一恒定的速率载荷。

断层的有限差分模型如图2所示，共划分了60个接触面单元，从A到G断层的接触面单元的编号为1-60。图中的边界条件为静力载荷作用下的边界条件。断层模型的岩体类型由上至下分为四层，选取的材料具体参数取值见表1。

图2 断层有限差分模型

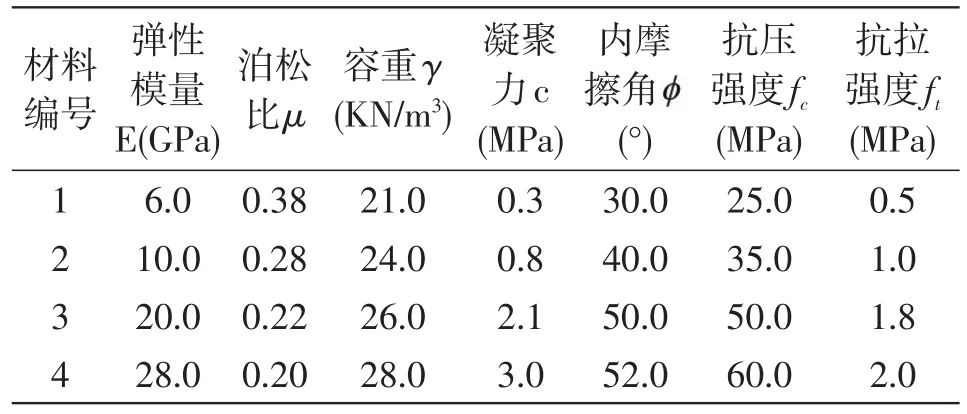
表1 岩体材料参数取值

模拟时首先计算岩体在自重荷载作用下的平衡状态，达到平衡状态后，在断层上盘右侧施加一均匀恒定的速度载荷，模拟断层滑动速率对断层滑动性质的影响。加载速率取值见表2。

表2 断层滑动速率

4 分析讨论

不同加载作用下的断层应力、能量释放以及断层各点随时间发展的能量释放情况如图3～图5所示。研究表明断层活动速率是影响断层滑动性质的一个重要因素，根据图3（a）～图5（a）可以看到，随着滑动速率的增加，断层的应力变化曲线变得较为光滑，速率越慢，断层破裂时发生的应力降越大；每一次应力降都会产生一次能量释放，速率越慢释放的能量也越大。对于本例中的拐折断层来说，远场加载速率越快断层分段破裂的效果越不明显（图5a中，达到极限摩擦应力前，断层的应力曲线并未产生明显的应力降），当速率降低时，断层分段破裂的效果在总应力曲线上表现明显（图3a中，在尚未达到极限摩擦应力前，应力曲线已产生了应力降，并释放能量）。

图3 V=1.5×10-7m/d时

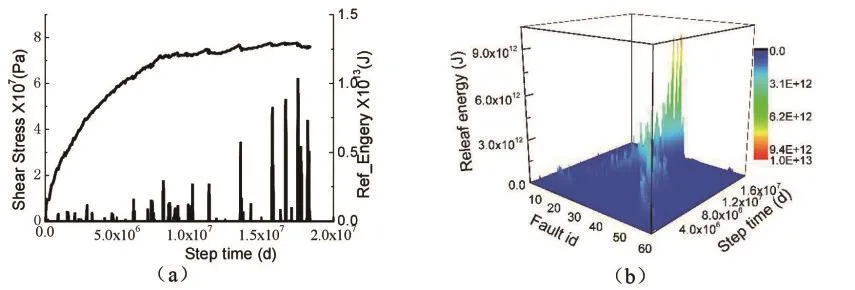
图4 V=1.5×10-6m/d时

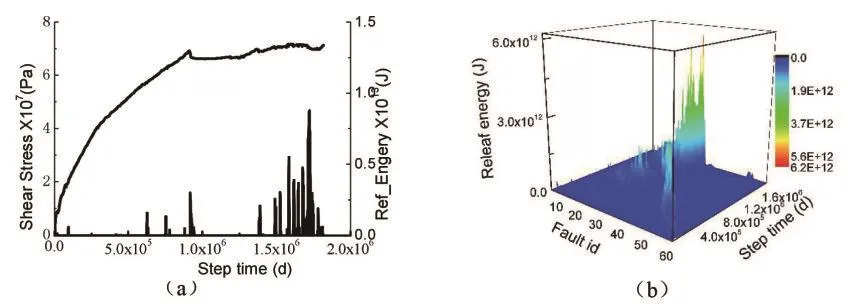
图5 V=1.5×10-5m/d时

不同速率作用下断层各点的能量释放随时间的发展变化如图3～5（b）所示。不同速率作用下各点的能量释放具有共同的特点：即：在远场载荷作用下，断层的破裂均是从两端开始向断层成核区发展，在成核区释放的能量最大，这对应于震源的破裂。但是加载的速率对能量释放过程及大小产生明显影响。速率越慢（图3b），断层由两端逐渐向成核区的破裂过程越明显，在加载过程中，断层从端部开始陆续有能量释放出，速率增加时（图5b），能量的释放更主要集中在成核区，加载过程中，断层端部能量释放并不明显。这表明断层滑动的速率越快，积累的弹性能越小，释放的弹性能可能更多的消耗于摩擦过程中，以集中形式的释放相对较小，产生大震的可能性较小；而对于滑动速率较低的断层，由于其加载速率缓慢，更加有利于应力以及弹性能的积累，破裂时会释放较大的能量，因此应引起警惕，注意监测。

5 结语

断层滑动失稳机制十分复杂，本文利用Fish语言在Flac接触面单元中嵌入速率-状态摩擦准则，是研究断层滑动失稳机制的一次有益尝试，也为进一步研究其他因素如断层不均匀性质、断层倾角等因素对断层滑动失稳的影响打下基础。