例谈拓展练习的点睛之笔
2018-03-16张志国
张志国

[摘 要]练习是学生掌握知识、形成技能及获取数学活动经验和数学思想方法的重要方式。在小学数学不断发展的今天,教师不仅关注着新授课的设计,更精心于练习题的选择,特别是最后的拓展练习,教师力图将这一环节浓墨重彩地呈现在学生面前,或承上启下,或拓展延伸,或发散思维。
[关键词]小学数学;习题;拓展练习;精心设计
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2018)05-0053-02
通过最近几次的学习更让我意识到,看似简单的习题背后,其实蕴藏着丰富、深刻的内涵,深埋着执教者对本课的独到见解与剖析。
一、巩固提升、丰富内涵、分解難度
【习题背景】
在“乘法的初步认识”同课异构的教研活动中,三位执教教师不约而同地在最后的拓展练习中安排了一道题目:请你用画图的方式表示5×2。
【片段回放】
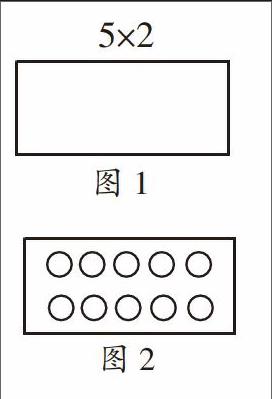
师:你能用画图的方式来表示算式5×2的意思吗?请画在作业纸的方框中。(出示图1)
(学生画图,教师巡视并展示学生作品)
师:老师也画了一幅。(出示图2)你看到了几个几?
师:老师聪明不聪明?只画了一幅图,却能表示出两种意思来。
师:现在看仔细了,老师要将图形变一变,你看看算式中哪个数也跟着变了呢?(出示图3)
如此深得三位执教教师青睐的题目肯定有它独特的价值所在。特级教师江萍在上本节课之前做了一次有效的前测,从前测的结果来看,学生对乘法算式已经有了一定的认识,对表内乘法的计算也有了一定的记忆,而对乘法意义的理解却存在困难,即对乘法算式表示几个几的问题还相当陌生。因此:
1.拓展为突破难点服务
纵观整堂课,再一次证明了学生对于乘法意义的理解确实存在困难。尽管学生经过激烈的争辩后,慢慢接受了根据图意有些乘法算式只能表示一个意思,如,教学主题图“游乐园乘坐小飞机”时,3×5和5×3只能表示5个3,而不能表示3个5。但如果没有图只有算式的情况下,3×5和5×3既可以表示5个3,也可以表示3个5。即便如此,当教师要求画图表示算式5×2 时,很多学生还是露出了为难之意。
片段回放中的拓展练习最大的用处在于,学生通过画图操作,既充分理解了乘法算式所表示的意义,又打破了之前“一图两式一意”的思维定式。矩阵图的出现让学生认识到,即使是同一幅图,只要从不同的角度去观察,就可以得到不同的含义,以图2为例,横着看是2个5,竖着看是5个2。最后,教师通过变一变,再一次加深了学生对“几个几”的理解:每增加一行就增加了1个5,每增加一列就增加了1个2,即份数在变,而每份数不变。
2.拓展为思维发展助力
数学教学不应只是灌输知识,更是传授一种思想方法。教师应在有限的40分钟里,让学生的思维得到有效的发展。
矩阵图的出现可以说是一种创新性的思维,“一图一式”向“一图多式”的创新,让学生体验了从不同角度去观察即有不同思路的乐趣。在实际教学中,教师应提倡标新立异,鼓励学生探究求新,激发学生在头脑中对已有知识进行调整、改组和充实的“再加工”,创造性地寻找独特简捷的解法,以促进学生形成思维的独创性。
二、逐层推进、激发思维、挖掘深度
【习题背景】
在求一个量是另一个量的几倍时,一开始学生接触到的都是大数与小数的比较,而且这两个数通常都成整数倍关系,因此,学生一拿到练习便用大数除以小数的方法来解决,而忽略了要先分析究竟是谁与谁在比较的问题,没有明确谁是标准量,这给今后继续学习用乘除法解决问题埋下隐患。为了去除隐患,打破思维定式,在教学“倍的认识”时,教师精心准备了拓展练习。
【片段回放】
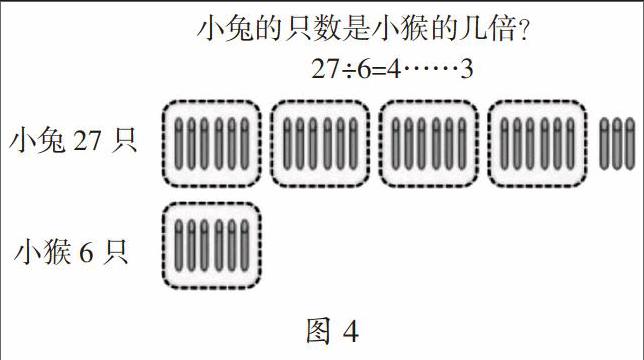
师:(出示图4)生活中有没有这样的关系?那是几倍?
生1:4倍多一些,不到5倍。
(课件出示图5,教师将小兔的只数不断变少,小猴的只数不变)
师:现在小兔的只数和小猴的只数是什么关系?
生1:同样多。
生2:小兔的只数是小猴的1倍。
生3:小猴的只数是小兔的1倍。(教师给予肯定)
师:如果老师将小兔的只数继续减少,会出现怎样的情况?
生4:1倍都不到了。
师:(出示图6)是这样吗?现在还是以谁为标准量?
生5:小猴。
师:现在小兔的只数是小猴的……
生6:一半、半份。
师:以后我们可以用适当的数表示一半或半份。
1.拓展需找准支点
不论是一、二年级的比多少,还是三年级“倍”的学习,或是今后“比”的认识,追根究底都是两个数大小的比较,其中的解题关键在于谁和谁比、谁是比较量、谁是标准量。因此,1倍关系的建立是学生打破“大数除以小数”思维定式的支撑点。课堂上,教师通过课件展示,不断变化小兔的只数,同时追问:“现在小兔的只数是小猴的几倍?”当小兔的只数和小猴的只数一样多时,学生既可以说小兔的只数是小猴的1倍,也可以说小猴的只数是小兔的1倍。再继续变化小兔的只数时,因为小猴的只数始终不变,始终作为一个不变的标准量,学生自然而然地发现两者“1倍都不到”的关系,即小数与大数的比较。通过比较量的千变万化和标准量的一成不变,水到渠成地解决了这一教学难点。
2.拓展应步步为营
看到图4时,一开始学生觉得不是整数倍就不能解决,于是教师设计了三个问题。问题1:“对于这些数量之间存在的倍数关系,你有什么问题或新的想法?”(试图引出非整数倍关系),学生沉默。问题2:“你怎么比较两个量之间的关系?比如小兔的只数是小猴的几倍?“学生摇头表示不行。问题3:”生活中有没有这样的关系?那是几倍?”为了打破学生头脑中建立的不规范的模型,教师一再追问,步步为营,终于冲破了非整数倍的思维定式,学生得到了“4倍多一点,不到5倍”的概念。
三、一题多用、多项并举、拓宽广度
【习题背景】
教学“认识小数”时,几乎是小数和分数充斥着整个课堂,让学生多有几分烦躁之意。如何在一些传统的练习之后让学生继续保持“心动”的感觉,这就要教师在拓展练习中给学生带来新的认识,以触发学生练习的动力。
【片段回放】
教师出示图7,并设计了三个问题。
问题1:估计一下,芳芳家到学校的距离是多少?
问题2:强强家到学校的距离是2.5千米,指一指强强家的位置大概在哪里?
问题3:根据这些信息,你还能提出哪些数学问题?
别出心裁的拓展练习让人一开始误以为“跑题”了,但从学生的课堂表现来看,学生综合运用了多种知识点,让本题焕发出了别样的精彩。因此:
1.拓展要多样生长
本题中将估计、推测等元素巧妙地融合于实际问题中,一改“教师供给”为“学生创编”,让学生从被动的接受者转变主动的创造者。学生根据条件“明明家距离学校1.6千米”,再借助“线段图”这个半具象的支撑,估计、推测都更加有理有据,再自己提出问题并解答。类似的拓展练习,不仅巩固了本节课的知识,而且融入了估算、方位、线段图等知识,促发了多样的生长点。
2.拓展要耐心等待
问题3较为开放,因为题目所给的信息实在太有限,所以一开始部分学生面露难色。这时,教师并不急于叫某位优等生回答以打破僵局,而是引导学生同桌合作讨论,可以提出哪些问题,并试着回答自己提出的问题,让同桌判断是不是有道理。经过短短几分钟的讨论之后,很多学生已经迫不及待地要把自己设计的问题说出来考考大家了。因此,很多时候,教师要学会耐心等待,允许学生有充分的思考时间,要坚信:一个苹果交换一个苹果,最后得到的还只是一个苹果,但是一种思想交换一种思想,就会得到两种不同的思想。
在拓展教学中,数学是深邃而美丽的,拓展教学所呈现、引导出的数学思维方法是宽泛的。从生命成长的角度来看,拓展教学能够激发学生形成独特的、多元的看待世界的方式——这也是学生未来应当具备的基本素养。
(责编 李琪琦)
