条分缕析——建模解应用题的思维特征
2018-03-16陈晓燕
陈晓燕


如何解应用题呢?首先,把实际问题数学化,也就是用数学语言加以抽象与概括,即数学地审题;其次,从数学角度刻画或反映实际问题,得出实际问题的数学描述,即建立数学模型;再次,通过推理、演算在数学模型中解决问题,并还原或说明数学结果所反映的实际问题,即“解”与“答”.解题步骤的流程图如下:
其中,“建立数学模型”是解应用题的关键,很多同学往往审题不清,无法进入分析问题、解决问题的环节,这就需要我们把握数学应用题的解题特点,养成“条分缕析”的思维习惯,充满信心地建构相应的数学模型.本文以两道高考模拟试题为例,为同学们剖析数学应用题的思维要求.
1.分级概括、去粗存精——简化问题背景
数学应用题源于生活,问题的背景包含很多生活化的信息,建模需要的量与量的相等和不等关系,量的约束条件等均蕴含在其中,这就需要我们学会阅读、分析和理解,学会将文字语言叙述转译成数学符号语言.我们可以将问题中的信息分为三个层级,浅层:可以忽略的铺垫介绍;表层:能够理解的基本关系;深层:反映本质的关键信息.浅层信息可以简去,表层信息直接转换成数学语言和符号,深层信息需要仔细推敲、重点突破.
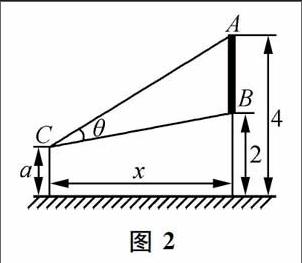
问题1中的“如图,墙上有一壁画,最高点A离地面4m,最低点B离地面2m”,“A离地面4m”、“B离地面2m”是表层信息,需要直接标注在图上,其他的均是浅层信息直接忽略.问题2中的“某宾馆在装修时,为了美观,欲将客房的窗户设计成半径为Im的网形”,只有“圆的半径为1 m”是表层信息,需要直接标注在图上,其他的均为浅层信息直接忽略.而问题1中的“观察者离墙多远时,视角θ最大”,问题2中的“四根木条将网分成如图所示的9个区域,其中四边形ABCD为中心在圆心的矩形”是深层信息,是问题的突破口以及解题的关键所在,需要认真思考和推敲,准确地用数学语言进行转化,
“分级概括”不仅去粗存精、用简洁的数学语言表征信息,而且简化了问题的背景、突出问题解决的重点.很多同学在审题时,由于没有掌握这种方法,往往身陷冗长的文字而无法自拔,进而失去解决问题的信心.
2.逐层抽象、重点突破——加工关键信息
应用题中的深层信息是建模的关键,基于不同的特征,我们要学会相应的抽象方法.问题1中的信息“观察者离墙多远时,视角θ最大”是一种典型的最优化问题的表征.虽然从字面上理解是求“离墙多远”,即“求x”,事实上需要关注对象却是“视角θ”.对于最优化问题,我们常用的方法是“将需要最优的量作为目标,建立目标函数”.这里要将“视角0”的某一个函数值(正弦、余弦或正切)作为因变量,“x”作为自变量,建立等量关系(解析式),并给出“x”的相应范围(定义域).这样处理后,问题转化为:“结合图形特征,如何求视角θ?”这是个表层的问题了,问题2中的深层信息“若四根木条总长为6m,求窗口ABCD面积的最大值”.也是最优化问题,处理方法类似.
3.合理比析、设计模型——解决实际问题
在概括、抽象的基础上,我们可以着手设计数学模型,进行建模.但是,思考问题的视角不同,所选择的模型也不一樣,解决数学模型的方法就有难有易,需要我们合理比析,做出选择.
(1)【问题1】的比析
