基于非线性规划的重力坝深层抗滑稳定优化算法研究

李 泽， 刘 毅， 胡 政， 周 宇

(昆明理工大学 建筑工程学院， 云南 昆明 650500)

1 研究背景

重力坝是依靠自重产生的抗滑力来挡水的水工建筑物，是水利水电工程中一种常见的坝型。由于重力坝具有较好的安全性和经济性，其在水利水电行业得到了广泛的应用。随着水电建设的发展和建设规模的日益增大，具有完整基岩的重力坝址越来越少，大部分重力坝均修建在地质条件复杂的岩基上，因此复杂坝基的重力坝抗滑稳定问题变得日益突出[1-6]。诸多学者对重力坝的抗滑稳定分析一直在进行研究，取得了较大的成果[7-11]。其中郭明伟等[12]对混凝土重力坝双滑面抗力方向角的取值研究取得了较大成果。

重力坝坝基岩体中存在着大量的软弱结构面时，对坝体抗滑稳定将产生不利影响，当作用在坝体及岩体上的荷载达到一定值时，坝基会沿着一个或多个软弱结构面组成的复合滑面发生破坏。根据重力坝坝基软弱结构面产状的不同，重力坝坝基深层滑动破坏可分为4种类型[13]：单斜剪切滑动破坏、双斜剪切滑动破坏、尾岩抗力体挤压破坏和尾岩抗力体隆起破坏。在这4种类型中，最常见的类型为：单斜剪切滑动破坏、双斜剪切滑动破坏。

单斜剪切滑动破坏属于单滑面情况，其计算比较简单，一般参照重力坝沿建基面滑动的抗滑稳定公式进行计算。双斜滑动稳定性分析较单斜剪切滑动破坏复杂，其计算方法主要有3种：被动抗力法、等安全系数法、剩余推力法。其中等安全系数法为水利行业的重力坝设计规范所采用。等安全系数法的主要思想是：采用抗剪断强度公式分别核算两个滑面上的抗滑安全系数，并令这两个安全系数相等，然后采用迭代法确定安全系数的值[14]。

等安全系数法主要可用于以下两类深层抗滑稳定的计算：第1类是坝体带动一块基岩沿缓倾角并露头的连续双滑动面滑动；第2类是坝基缓倾软弱结构面未露头，也无可压缩层，但可能发生部分下游基岩的剪断而产生滑动。对于第1类情况,可应用等安全系数法直接计算抗滑稳定的安全系数；但对于第2类情况，下游基岩的断裂面一般难以确定，现阶段的设计方法一般是先假定一个下游基岩的断裂面，再进行抗滑稳定分析，然而此方法并不能够确定

最不利的下游基岩的断裂面。

基于上述分析，针对坝基缓倾软弱结构面未露头，但可能发生部分下游基岩的剪断而产生滑动的情况，本文提出了一种重力坝坝基双斜滑动临界破坏滑面的计算方法。

2 重力坝坝基深层抗滑稳定计算

当坝基深层存在缓倾角结构面，按地质资料可分为3类，分别是单滑动面、双滑动面和多滑动面，按此3类进行抗滑稳定分析。其中最常见的为双滑动面，图1为双滑面典型示意图。

图1 重力坝坝基双滑动面典型示意图

采用等安全系数法计算深层抗滑稳定，可按抗剪断强度公式或抗剪强度公式进行计算，本文针对图1所示的双滑面情况采用抗剪断强度公式进行计算[14]。

考虑ABD块的稳定，则有:

(1)

考虑BCD块的稳定，则有：

(2)

3 基于非线性规划的重力坝深层抗滑稳定的优化算法模型

3.1 重力坝坝基深层抗滑稳定计算的相关参数

重力坝坝基缓倾软弱结构面未露头，部分下游基岩发生剪断而产生滑动的双斜滑动受力图如图1所示。图1中：ADC为重力坝建基面，AB为缓倾软弱结构面，BC为下游基岩发生剪断的破坏滑面，BD为滑块ABD、BCD的分界面。根据重力坝的实际情况，可确定其计算参数，主要包括：重力坝坝体、基岩几何参数、材料参数(包括坝体、基岩和软弱结构面的容重、凝聚力、摩擦角)、荷载参数。

3.2 非线性数学规划模型

(3)

3.2.2 目标函数 对于重力坝深层抗滑稳定问题，一般定义安全系数为：K′=抗滑力/滑动力。本文将重力坝抗滑稳定安全系数K′作为目标函数，并寻求其对应于下游基岩岩体临界破坏滑面BC的最小值。

3.2.3 等安全系数法约束方程 根据重力坝深层抗滑稳定计算的等安全系数法，图1所示的重力坝在发生双斜面滑动时，根据式(1)、(2)，ABD、BCD滑块应满足以下约束方程:

(4)

3.3 求解重力坝坝基双斜滑动临界破坏滑面的非线性数学规划模型

求解重力坝坝基双斜滑动临界破坏滑面的非线性数学规划模型的目标函数为安全系数，约束条件为等安全系数法方程。数学模型具体表达式为：

(5)

4 非线性规划

目前对于非线性规划模型的求解，本文采用序列二次规划算法(SequentialQuadraticProgrammingMethod)[15]求解本文的非线性数学规划模型，计算结果包括下游基岩发生剪断的临界破坏滑面及其对应的抗滑稳定安全系数。本文的程序框图如图2。

5 算例分析

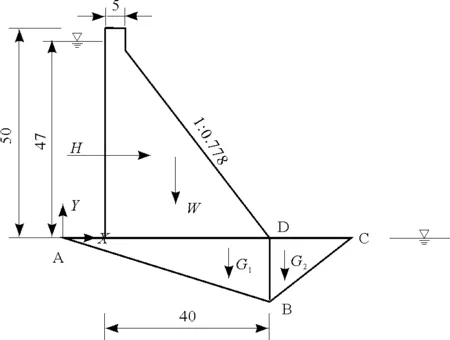
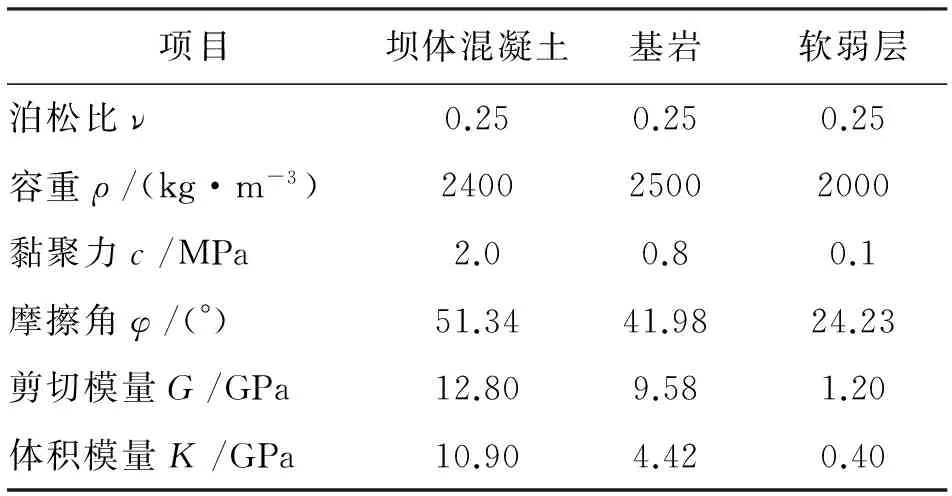
如图3所示的重力坝，坝高为50.0m，坝顶宽度5.0m，坝底宽度为40m，下游面坡度为1∶0.778，上游正常蓄水位为47.0m，下游水位为0.0m。ADC为建基面，AB为一缓倾软弱结构面，其倾角为16.7°，BC为下游基岩发生剪断的滑裂面。A、B、D3点的坐标分别为：A(0, 0)、B(50, -15)、D(50, 0)，C点坐标(xC,yC)为决策变量。由于建基面为水平面且C点必须位于D点右侧，因此取yC=0，50

图2 程序框图

根据以上参数并结合图1、图3，进行重力坝抗滑稳定计算的受力分析；并结合数学模型的目标函数、约束条件，可形成求解重力坝下游岩体剪断破坏临界滑裂面及其对应的安全系数的非线性数学规划模型如下。

采用序列二次规划法求解上述非线性数学规划模型，计算结果为：下游基岩发生剪断破坏的临界滑面C点的坐标为(0.0，76.74645)，临界滑面BC滑面的倾角β,临界滑面BC的长度为30.6655m，对应于临界滑面BC的重力坝深层抗滑稳定安全系数K=3.97，岩块ABD与岩块BCD之间的作用力Q

=15 415 120N。

图3 重力坝算例示意图 (单位m)

(6)

为了更好地验算本文所提方法的正确性，本文采用有限元差分法对重力坝进行三维非线性数值模拟分析。根据工程经验，本文三维数值模型计算深度按照重力坝高度的2倍取值；计算宽度取为重力坝上、下游面到模型边界1.5～2.0倍的重力坝高度，模型划分共有32 964个节点，21 716个六面体单元，缓倾软弱结构面厚度取0.2m(三维数值模型如图4所示)。重力坝、基岩和软弱层采用实体单元中的六面体单元进模拟，重力坝模型的计算荷载按现行规范取值[14]；模型坝体及基岩的物理力学参数如表1所示。

为了与本文所提方法的计算结果进行比较，在运用有限差分法进行三维非线性数值模拟计算时采用降强法求解基岩屈服破坏时的强度储备系数，即在计算迭代过程中同时降低材料的黏聚力c和摩擦角φ，直到基岩屈服区贯通失去承载能力为止。强度储备系数的计算结果是4.0，即将基岩和软弱层的黏聚力c和摩擦角φ降低4倍的条件下屈服区分布如图4所示，图5为基岩屈服区局部放大示意图，表2为本文方法和有限差分法计算得到的安全系数统计表。

图4 强度储备系数为4.0的重力坝塑性区分布示意图

在图4、5中深色区域为基岩和软弱层的屈服区，AB为已知的软弱层位置，BC为本文所提方法计算得到的临界滑裂面位置。

图5 强度储备系数为4.0的重力坝塑性区分布放大示意图

项目坝体混凝土基岩软弱层泊松比ν0.250.250.25容重ρ/(kg·m-3)240025002000黏聚力c/MPa2.00.80.1摩擦角φ/(°)51.3441.9824.23剪切模量G/GPa12.809.581.20体积模量K/GPa10.904.420.40

表2 两种方法计算结果统计表

由图可知，基岩屈服区的位置位于重力坝坝趾下部基岩至软弱层区域，且在强度储备系数取4.0的条件下由有限差分法得到的屈服区正好沿着BC线贯穿。另外，本文所提方法计算的安全系数为3.97，有限差分法的为4.00，两种方法计算得到安全系数非常接近。有限差分法计算的结果验证了本文方法的正确性。

6 结 论

现行重力坝规范对于重力坝深层抗滑稳定分析规定采用的等安全系数法一般只适用于滑面已知的情况，对于坝基缓倾软弱结构面未露头，但可能发生部分下游基岩的剪断而产生滑动的情况，下游基岩的断裂面一般难以采用等安全系数法确定。故提出了一种将下游基岩发生剪断破坏滑面的位置变量作为优化变量，以重力坝深层抗滑稳定安全系数作为目标函数，同时以等安全系数法方程作为约束条件，建立重力坝深层抗滑稳定性分析的非线性数学规划

模型。

本文采用优化方法求解下游基岩发生剪断的最不利临界破坏滑面及其对应的最小安全系数。通过算例分析，对比了本文方法与有限差分法所得安全系数的大小，可知该方法概念明确、计算精度高、工程应用简便，可将其应用于重力坝深层抗滑稳定的分析。在今后的研究中，需在本文工作基础上对不同类型的滑动破坏模式进行分析研究。

[1] 潘家铮. 建筑物的抗滑稳定和滑坡分析[M].北京：水利出版社, 1980.

[2] 陈祖煜,陈立宏. 对重力坝设计规范中双斜面抗滑稳定分析公式的讨论意见[J]. 水力发电学报,2002,21(2):101-108.

[3] 黄照宾. 论重力坝深层抗滑稳定问题[J]. 城市建设理论研究:电子版,2013(29).

[4] 郑颖人,赵尚毅. 边(滑)坡工程设计中安全系数的讨论[J]. 岩石力学与工程学报,2006,25(9):1937-1940.

[5] 毛巨省. 三峡左厂3号坝段坝基深层抗滑稳定性有限元分析[J]. 西安科技大学学报,2006,26(3):296-299. [6] 周 伟,常晓林,袁林娟. 对重力坝设计规范中双斜面抗滑稳定的补充讨论[J]. 水力发电学报,2005,24(2):95-99.

[7] 蒋春艳,常晓林,周 伟. 用于重力坝抗滑稳定分析的分项系数有限元方法[J]. 水力发电学报,2006,25(2):16-20.[8] 于 沭,段庆伟,徐能雄. 龙口水利枢纽厂房坝段深层抗滑稳定分析[J]. 资源与产业,2007,9(3):119-121.

[9] 王义锋,章 青. 基于界面元法的向家坝重力坝深层抗滑稳定分析[J]. 岩土力学,2009,30(9):2691-2696.

[10] 马 刚,常晓林,周 伟,等. 基于Cosserat理论的重力坝深层抗滑稳定分析[J]. 岩土力学,2012,33(5):229-236. [11]SUHuaizhi,HUJiang,LIJinyou,etal.Deepstabilityevaluationofhigh-gravitydamundercombiningactionofpowerhouseanddam[J].InternationalJournalofGeomechanics,2013,13(3):257-272.

[12] 郭明伟,王水林,邓 琴,等. 混凝土重力坝双滑面抗力方向角的取值研究[J]. 岩土力学,2012,33(6):1864-1868.

[13] 郭利娜,李同春,赵兰浩,等. 重力坝深层抗滑稳定分析[J]. 人民黄河,2011,33(1):101-102105.

[14] 中华人民共和国水利部.SL319-2005 混凝土重力坝设计规范[S]. 北京：中国水利水电出版社,2005.

[15] 杨庆之. 最优化方法[M]. 北京：科学出版社,2015.