二次重现期在暴雨洪涝灾害中的应用研究

2018-03-16范嘉炜袁明道马妍博潘展钊张旭辉

水资源与水工程学报 2018年1期

范嘉炜，袁明道，马妍博，潘展钊，张旭辉

(1.广东省水利水电科学研究院，广东广州 510635；2.广东省大坝安全技术管理中心，广东广州 510635；3.广东省山洪灾害突发事件应急技术研究中心，广东广州 510635)

1 研究背景

近年来，受极端水文气候的影响，我国中南部地区频繁遭遇强降雨袭击，加剧了城市以及周边乡镇的内涝问题[1-3]。虽然内涝问题是由多种因素共同作用下而导致的，但短时间内的强降雨是众多因素中一个最为主要的诱发因素，城市的防洪排涝能力不足以应对暴雨的侵袭，会直接造成城市内涝的发生。当降水集中且强度较大时，加之市区排水设施落后，建设标准不达标等因素，受灾情况更为严重。内涝的发生给城市的交通运输、通讯、电力等重要系统带来了严重的破坏，给居民的日常生活造成了诸多不便和影响，巨大的经济损失远远超过由暴雨等极端天气导致的直接经济损失[4-5]。

因此,为加强城市防洪减灾能力，提升现有城区排水设施标准，倪增华等[6]建立了以年降雨均值和年降雨极值均值为变量的联合分布，提出在实际工程中采用联合重现期下的设计值作为防洪排涝标准更安全。曹伟华等[7]指出仅基于单一致灾因素的重现期估算会低估致灾风险，多因素下的条件重现期更能准确地反映强降雨的致灾危险性，为实现防灾减灾规划和预警提供科学依据。刘成林等[8]提出了基于降雨特征变量的分析方法，并指出合理确定降雨特征量是防洪排涝系统设计、调度运行的关键。刘曾美等[9]提出了基于涝区暴雨和承泄区水位的治涝标准分析方法，并用联合分布模型描述其遭遇几率。黄宁[10]以浙江省某城区为研究对象，在分析降雨事件的基础上，对内涝风险评估方法进行了验证。

在传统的水文计算中，通常采用单变量方法估算降雨特征值，忽略了变量间的相关性，显然这不利于准确评估暴雨致灾事件[11]，对合理设定城市防洪排涝标准也有较大的影响。本文以以高州市大坡站1967-2016年降雨资料为依据，应用Copula函数[12]和二次重现期理论[13-15]，建立不同历时降雨组合的联合分布函数，对比分析了传统重现期和二次重现期值的差异性，并计算了3种重现期法下的设计值，分析结果可为研究区洪涝灾害防治工程设计、合理制定防洪排涝标准提供参考依据。

2 研究方法

2.1 G-H Copula函数

Gumbel-Hougaard (G-H) Copula函数属Archimedean-Copula函数中的一种[12]，它能够将多个变量的边缘分布联结起来，反映变量之间的相关关系。目前在水文领域被广泛应用。Copula函数由于表达形式简洁易懂，且由于在其构造基于多变量的联合分布函数时可以变换多种形式，在水利工程中也被广泛应用于分析实际问题。

Gumbel-Hougaard(G-H)Copula的表达式为：

C(u1,u2)=exp(-((-lnu1)θ+

(-lnu2)θ)1/θ),θ∈[1,∞)

(1)

式中：θ为函数参数；u1和u2为边缘分布函数。

参数θ的估计通常采用相关性指标法，通过建立Kendall秩相关系数τ与θ的关系推求θ的值。τ与θ的关系可由式(2)表示：

(2)

而τ可由式(3)推求：

(3)

式中：τ为Kendall秩相关系数; sign为符号函数; (xi,yi)为测点据;n为实测序列长度。

2.2 传统重现期与二次重现期

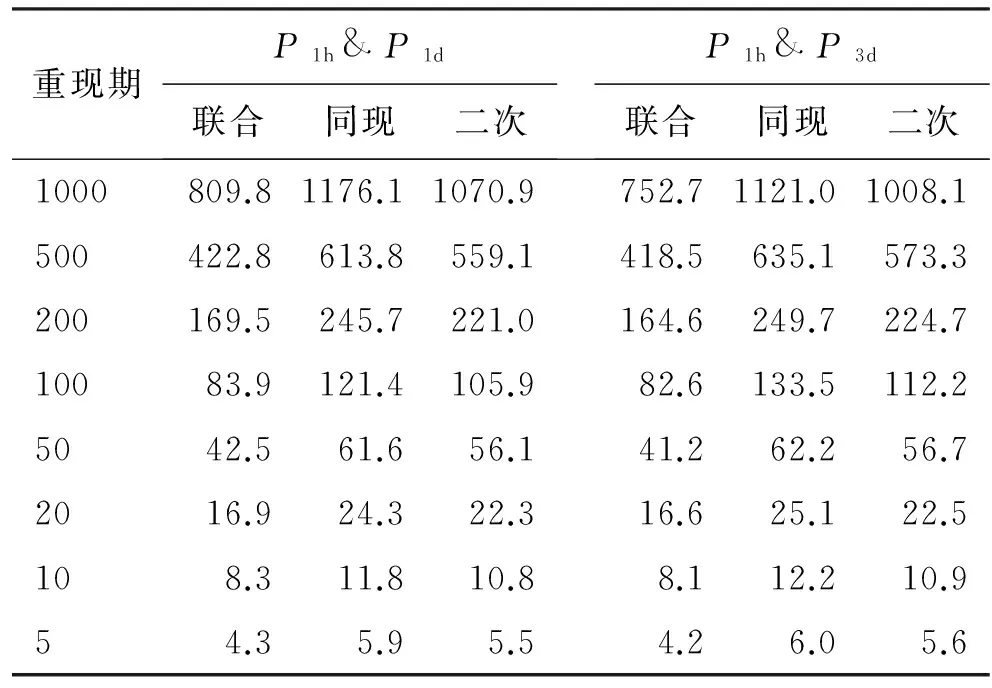
传统重现期分为联合重现期和同现重现期，目前被水文界普遍认可。变量的重现期与它们的联合分布函数C相关联，C值越大，说明发生该水文事件的可能性越小，相应的重现期就越大。

若取降雨组合序列P1和P2为研究对象，将边缘分布函数以式(4)表示：

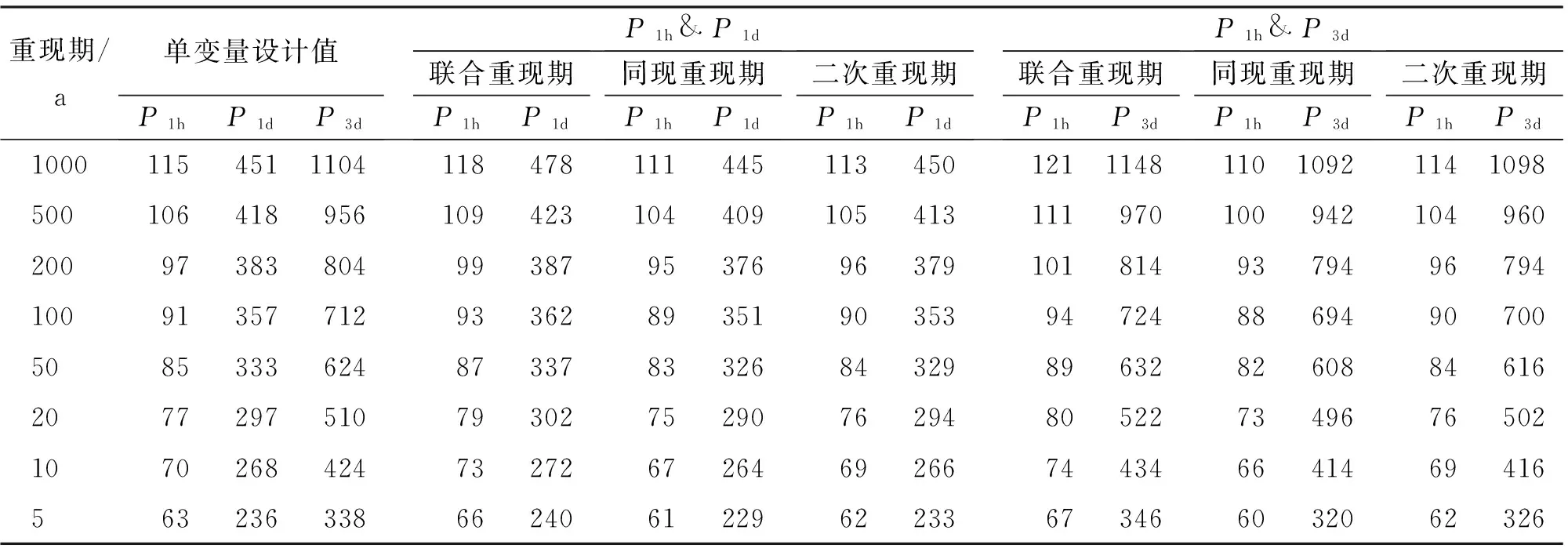
u=f1(x)=P(P1

v=f2(y)=P(P2

(4)

对于P1和P2其中之一超过设定阈值时的工况以式(5)表示；对于P1和P2两者同时超过设定阈值时的工况以式(6)表示。目前水文界称两者为联合重现期和同现重现期，同属传统重现期计算法。P1和P2为设定的阈值，u、v、C(u,v)意义同前：

(5)

(6)

值得注意的是，目前在水利工程设计中，通常选择偏保守的联合重现期确定研究对象的设计值，然而在给定重现期条件下会对应无数多组不同的变量组合，每组变量都可以对应一个危险域[16-17]，因此对于相同的重现期值，样本所对应的危险域和安全域却不相同，直接导致了危险域之间互相矛盾的现象[17]。显然，这种定义是有缺陷的。针对同现重现期而言，这个问题依旧存在。考虑到在定义传统重现期时导致危险域不唯一的情况，SALVADORI[13-15]提出了一种新的定义重现期的方法，将Kendall测度Kc应用在重现期定义中，令联合概率小于等于t使得多变量分布函数与一维分布相关联。这种定义方式从根本上解决了传统重现期法的不合理性，使得变量组合在给定重现期或风险概率情况下有唯一危险域与之对应。函数Kc可用式(7)表达，式中t∈(0,1)：

Kc(t)=P(W≤t)=P(C(u,v)≤t)

(7)

Kc测度在Gumbel-Hougaard(G-H)Copula函数中表达形式如下：

(8)

式中：θ为G-H Copula参数，φ(t)=[-ln(t)]θ为生成元。

因此结合重现期定义，二次重现期可表达如下：

(9)

考虑到二次重现期在定义危险域中的优越性，本文在对高州市暴雨致灾事件进行风险评估时采用第二重现期与传统重现期法分别计算，并就计算的设计值和误差进行了全面的对比和分析。

3 研究区域分析

以高州市大坡站1967-2016年降雨资料为依据，选取年最大1h降雨并以此时间为基准选取连续1d、3d降雨序列，建立1h～1d、1h～3d降雨组合样本。样本数据采用P-Ⅲ型曲线频率适线，分析结果见表1。

表1 高州市大坡站各时段暴雨频率表 mm

通过式(3)计算得到P1h&P1d组合的秩相关系数τ为0.454，P1h&P3d组合的秩相关系数τ为0.130，故两组变量间存在一定的正相关性，故分别建立降雨组合的联合分布函数，其中函数参数θ由τ-θ关系推求：

P1h&P1d:C(u,v)=exp(-((-lnu)1.83+

(-lnv)1.83)1/1.83)

(10)

P1h&P3d:C(u,v)=exp(-((-lnu)1.15+

(-lnv)1.15)1/1.15)

(11)

为了确认G-H Copula函数是否能准确拟合变量间的相关关系，本文采用较为直观的图形分析法进行拟合优度评价[18]。该方法将经验概率和理论概率分别标绘于同一图中，若当散点均分布在45°线周围时，则变量组合具有较好的相关性。变量组合的经验概率值可由Femp(xi1,xi2)表示如下：

(12)

式中：N为实测序列的总对数；ni为序列中小于等于(xi1,xi2)的对数。

将以上两组变量为研究对象计算得出的理论频率值和式(12)得到的经验频率值点绘于图1中。从图1可以看出，Gumbel-HougaardCopula构造的两组降雨序列联合分布的经验点值与理论计算值均匀分布在45°线附近，因此G-HCopula拟合效果良好。

由此建立基于G-HCopula函数的降雨组合在3种重现期下的联合分布模型和对应等值线图，并以P1h&P1d组合为例，绘于图2。P1h&P3d联合分布特征与之相近，篇幅所限，故省略。从图2可见，联合重现期和二次重现期的等值线图的分布特征较相近，当取同样的降雨组合时，二次重现期的取值略大于联合重现期，相比而言，同现重现期图的分布形态较前两者有较大不同。

根据传统重现期的定义，在相同的单变量重现期条件下，联合重现期值一定小于同现重现期，且二次重现期值处于前两者之间，表2列出的3种重现期法下的降雨组合计算结果也充分反映了这种分布规律。例如在单变量条件下，取P1h和P1d均为200年一遇，则联合重现期为169.5a，同现重现期为245.7a，二次重现期为221.0a；取P1h和P3d均为1000年一遇，则联合重现期为752.7a，同现重现期为1 121.0a，二次重现期为1 008.1a。

图1 理论—经验频率拟合图

图2 不同重现期下的P1h & P1d组合联合分布与相应等值线图

在进行城市内涝防治工程设计中常常需要估算不同重现期下的降雨设计值，这对于合理确定排水管渠尺寸，实现工程效益与工程投资比最大化十分重要。在单变量的水文频率分析中，在给定的重现期下，存在唯一的设计值与之对应。但在有多个水文变量的情况下，无论重现期大小是否相同，都有无数种可能的设计值组合。由于没有与概率函数相对应的反函数，因而无法直接获得设计值。权函数法[17]作为新兴的设计方法，可以与联合分布模型相结合，估算最可能出现的组合设计值：

(um,vm)=arc maxf(u,v)

(13)

f(u,v)=c(u,v)f1(x)f2(y)

(14)

式中： (um,vm)为所求降雨设计值组合；c(u,v)、f1(x)、f2(y)意义同前。

表3列出了年最大1h降雨量与连续累积1d和3d降雨组合的设计雨量。从表3中可以看出，单变量降雨设计值分别小于和大于联合重现期与同现重现期条件下的降雨设计值，例如在P1h&P1d降雨组合下，重现期取500年一遇时，P1d设计值为418mm，小于联合重现期下的设计值423mm，大于同现重现期下的设计值409mm，而基于二次重现期的设计值为413mm介于以上两者之间且略小于单变量设计值，因此可以起到既满足防洪排涝设计要求，又可以降低工程经济成本的作用。

设计值的分布规律可简要概括为联合重现期>单变量重现期>二次重现期>同现重现期。出现以上分布规律的原因是由于联合重现期法扩大了事件的危险域，致使在同样的降雨组合下得到的危险事件发生的重现期较小，在相同的重现期条件下降雨组合的设计值较大；而同现重现期则与之相反，它缩小了事件的危险域，过高估计了危险事件的重现期，采用此方法会使降雨设计值偏小。

表2 不同历时降雨组合的3种重现期 a

表3 不同重现期下的降雨组合设计值 mm

表4列出了以P1h&P1d和P1h&P3d降雨组合为例，3种重现期设计值与单变量重现期设计值的误差。在P1h&P1d中，二次重现期的估算误差绝对值范围为0.22%～1.74%，最大误差均出现在重现期1 000a；联合重现期和同现重现期误差范围分别为1.04%～5.99%、1.33%～4.29%。在P1h&P3d中，二次重现期的估算误差绝对值范围为0.42%～1.89%，同样较联合与同现法误差为小。

表4 降雨组合设计值与单变量重现期设计值误差 %

4 结论

(1)工程设计中常常需要估算不同重现期下的降雨设计值，在考虑多个水文变量的条件下，会出现无数种可能的设计值组合。权函数法作为新兴的设计方法，可以与联合分布模型相结合，估算最可能出现的组合设计值。

(2)以年最大1h降雨与连续累积1d和3d降雨量为降雨组合，推求了基于3种重现期法下的重现期设计值与降雨设计值，通过对比和分析指出二次重现期能够有效避免对水文事件危险域过大或过小的估计。

(3)两种传统重现期方法由于受各自定义特点的约束，造成了在考虑危险事件时对重现期和设计值的估算出现偏差。但在一些有指定设计要求的工程中，可利用传统方法定义明确这一特点，结合“或”和“且”的设计理念，合理选择最佳的估算方法。在无特定要求的工程设计中，为了尽可能真实地反映降雨事件的实际特征，一般推荐采用基于二次重现期法的估计值。

(4)联合重现期估计设计值过大，在工程建设中偏保守，将造成施工费用偏高；同现重现期法估计的设计值过小，虽然造价较为经济，但在工程建设中存在风险。因此，为了经济合理地实施城市基础设施建设，实现防洪排涝能力最大化和施工成本最小化，二次重现期法可以作为确定排涝管渠规格等工程设计的重要参考。

[1]FONTANAZZACM,FRENIG,LALG,etal.Uncertaintyevaluationofdesignrainfallforurbanfloodriskanalysis[J].WaterScience&Technology(AJournaloftheInternationalAssociationonWaterPollutionResearch), 2011,63(11):2641-2650.

[2]IPCC.Climatechange2007:Synthesisreport[M].Cambridge:CambridgeUniversityPress,2007.

[3] 陆桂华,张亚洲,肖恒，等.气候变化背景下蚌埠市暴雨与淮河上游洪水遭遇概率分析[J].气候变化研究进展,2015,11(1)：31-36.

[4] 郭常安,邓立鸣.广州市中心城区内涝分析及对策[J].中国给水排水,2011,27(10):25-28.

[5] 莫建飞,陆甲,李艳兰,等.基于GIS的广西农业暴雨洪涝灾害风险评估[J].灾害学,2012,27(1):38-43.

[6] 倪增华,刘合香,罗彦丽，等.Copula函数在广西洪涝灾害的降水概率预测中的应用[J].气象研究与应用,2014,35(2):32-39.

[7] 曹伟华,梁旭东,赵晗萍，等.基于Copula函数的北京强降水频率及危险性分析[J].气象学报,2016，74(5)：772-783.

[8] 刘成林,周玉文,隋军，等.设计降雨特征的多变量分析方法[J].北京工业大学学报,2015,41(6):940-945.

[9] 刘曾美，陈子燊.基于两个致灾因子的治涝标准研究[J].水力发电学报，2011，30(3):39-40+49.

[10] 黄宁.降雨事件联合概率分析及其在城市内涝风险评估中的应用[D].杭州：浙江大学，2016.